改进的FOA算法在通用桥式起重机轻量化设计中的应用

刘 彬 蒋惠波 吴晓路

（济宁职业技术学院 济宁 272037）

改进的FOA算法在通用桥式起重机轻量化设计中的应用

刘 彬 蒋惠波 吴晓路

（济宁职业技术学院 济宁 272037）

针对传统FOA算法全局收敛能力差、易陷入局部极值的缺陷，提出了具有混 映射及协同进化功能的改进果蝇算法。首先利用Logistic混 映射功能在整个收敛域范围内搜索并初始化果蝇种群，保证算法的全局计算能力，然后根据当前果蝇个体的位置赋予搜索的方向与距离，以期全面提高算法的计算速度。采用两个优化函数测试改进后算法优化的特性，优化计算的结果显示了该算法具有良好的全局优化能力，在通用桥式起重机金属结构轻量化设计中的成功应用，体现了该算法在结构设计轻量化方面的优越性。

FOA Logistic 协同进化 优化设计

模拟果蝇觅食行为的果蝇算法［1］（Fruit Fly Optimization Algorithm - FOA）自2011年提出以来，因其简单的计算原理、快速的计算能力及良好的通用性，成为了智能优化领域新的研究热点。国内外研究人员以各自的研究背景为依托，提出了各种各样的改进FOA算法，以期提高其优化和解决实际问题的能力。Wang Li［2］等人采用FOA算法求解多维背包问题，使用二进制串表示问题的解决方案，并且将算法的进化定义为三个主要的搜索过程，通过数值算例的仿真及与其他算法的比较结果证明了该 算法可靠的计算能力；Li H.Z.［3］等人将FOA算法应用到广义回归神经网络中，将FOA算法同广义 回归神经网络结合，用于预测年度电力负荷状况；Yuan Xiaofang［4］等人为提高算法的全局搜索能力，采用了多个种群同时参与寻优迭代，提出了多种群优化算法（Multi-Swarm Fruit Fly Optimization Algorithm）。

笔者针对FOA算法进行了大量的研究，掌握了FOA算法的优化能力及其不足之处，针对传统FOA算法全局搜索能力差，迭代搜索的目标不明确等问题，本文提出了相应的改进方案。首先，初始化的果蝇种群采用Logistic混沌映射的方式产生，利用混沌的遍历性和随机性，在全局范围内随机的初始化果蝇种群，使算法在搜索初期具有较好的全局性。其次，利用果蝇个体间的位置关系，确定果蝇继续飞行的方向和距离，提高了算法的计算速度和收敛域最优点的精度。

1 改进的FOA算法

作为全新的基于果蝇觅食行为全局智能优化算法，FOA算法简单易理解，程序代码容易实现，和其他智能算法相比，FOA算法更简单、优化计算的稳定性更强，更容易转化为生产力。将传统果蝇算法同本文的改进方式结合，其优化计算的步骤如下：

4）利用已生成的随机矩阵，生成如图1所示的设计变量矩阵。

5）计算种群目标函数值fitnessm，

6）判断算法是否收敛，是则输出结果，否则执行下一步。

7）以当前最优果蝇为起点，种群中任意个体按照式（4）搜索新解。

8）返回步骤5。

2 数值算例验证

为验证算法的性能，采用了2个被广泛用来测试算法性能的优化测试函数。种群中包含的果蝇个体取Population=20，设计空间的维数分别取Design_ Num=10和Design_Num=30，最大迭代次数Max_ Num=400，收敛精度取为0.000001。分别运用FOA算法和改进后的算法对测试函数进行分析，优化的结果见表1，目标函数的迭代曲线如下图2、图3所示。

1）Rastrigin's function：Rastrigin是一个高度多峰的测试函数，在收敛域内存在多个局部极值，该函数考验算法的全局收敛能力。

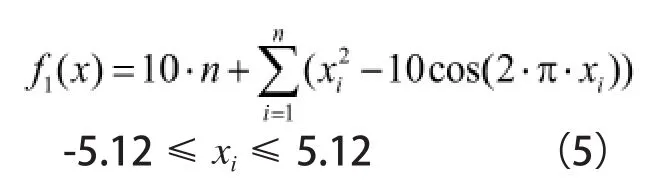
2）Rosenbrock's Valley：该测试函数也称为香蕉函数，其全局最优值分布在一个狭长的、平坦的谷底，很难搜索到全局最优值。

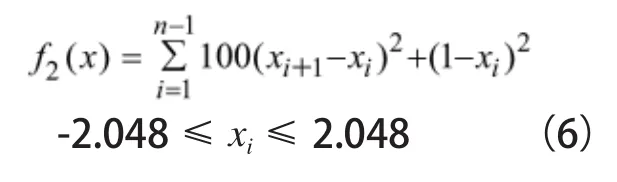
表1 测试结果

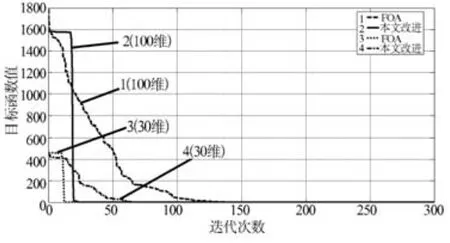
图2 测试函数1迭代曲线

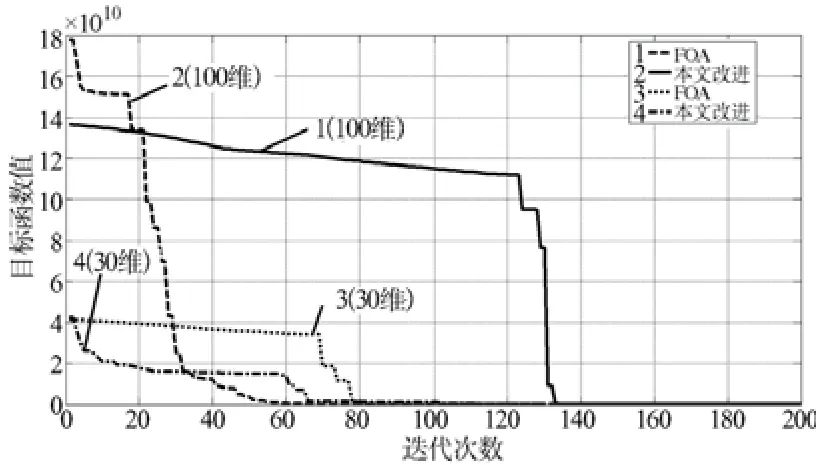
图3 测试函数2迭代曲线

参照图2、图3的迭代曲线及表1的计算结果可知，采用本文提出的改进方法同传统FOA算法相比，具有明显的优势，计算量上具有明显的降低趋势，而且计算精度更高，该算法具有应用于工程优化设计的潜力。

3 桥式起重机结构优化

以如图4所示的传统的桥式起重机作为优化的目标，选择能够直接影响起重机工作性能同时又能够改变起重机外观形态的10个变量作为设计变量，10个设计变量所代表的几何意义如图5和图6所示，分别是：主梁上盖板厚度4mm≤X1≤24mm，主梁下盖板厚度4mm≤X2≤24mm，主梁主腹板厚度4mm≤X3≤24mm，主梁副腹板厚度4mm≤X4≤24mm，主梁腹板高度400mm≤X5≤800mm，主梁腹板间距190mm≤X6≤290mm，端梁上下盖板厚度4mm≤X7≤10mm，端梁腹板厚度4mm≤X8≤10mm，端梁腹板高度388mm≤X9≤788mm，端梁腹板间距220mm≤X10≤320mm。本文选用起重量为5t，跨度10.5m的通用双梁桥式起重机，对其结构进行分析及轻量化设计。

图4 通用桥式起重机结构模型

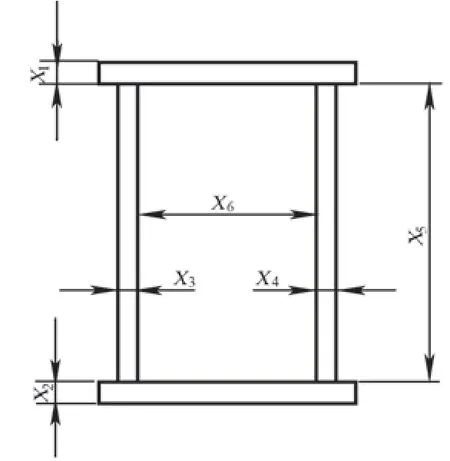
图5 主梁截面尺寸表达

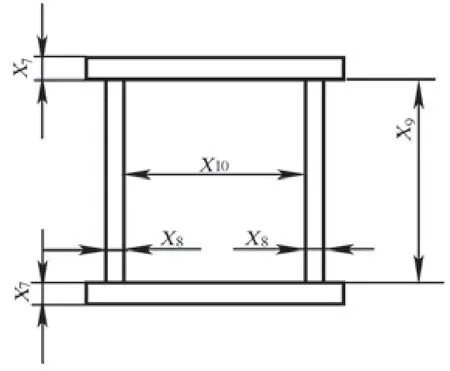
图6 端梁截面尺寸表达

结构轻量化设计的目标是在保证满足结构设计要求的前提下，所使用的材料最少，即结构质量最轻，因此可以将起重机轻量化设计的目标函数定义为：

约束条件：桥式起重机结构设计需要遵照起重机行业设计规范GB 3811—2008，保证起重机结构设计的强度、刚度及稳定性的设计要求，并按照实际制造工艺条件及尺寸限制等方面的限制。

采用本文改进算法对通用桥式起重机金属结构进行轻量化设计，对算法进行20次独立的优化计算，将优化所得结果列于表2中，表2中包含了20次独立优化计算的最优、最差及平均计算结果。通过表2中数据可知，采用改进的FOA算法对通用桥式起重机进行轻量化设计可以获得较好的计算结果，原始设计参数为某款通用桥式起重机的实测数据，设计余量较大，而优化后的最优解相较原始参数目标函数下降约36.56%，若该起重机采用本文方法进行设计，可以较大程度的节约成本，节约原材料的损耗，获得可观的经济效益。对比优化后的平均结果和最优解，目标函数的变化率仅为4.67%，本文算法的稳定性（鲁棒性）较好，计算结果不会出现较大的波动。

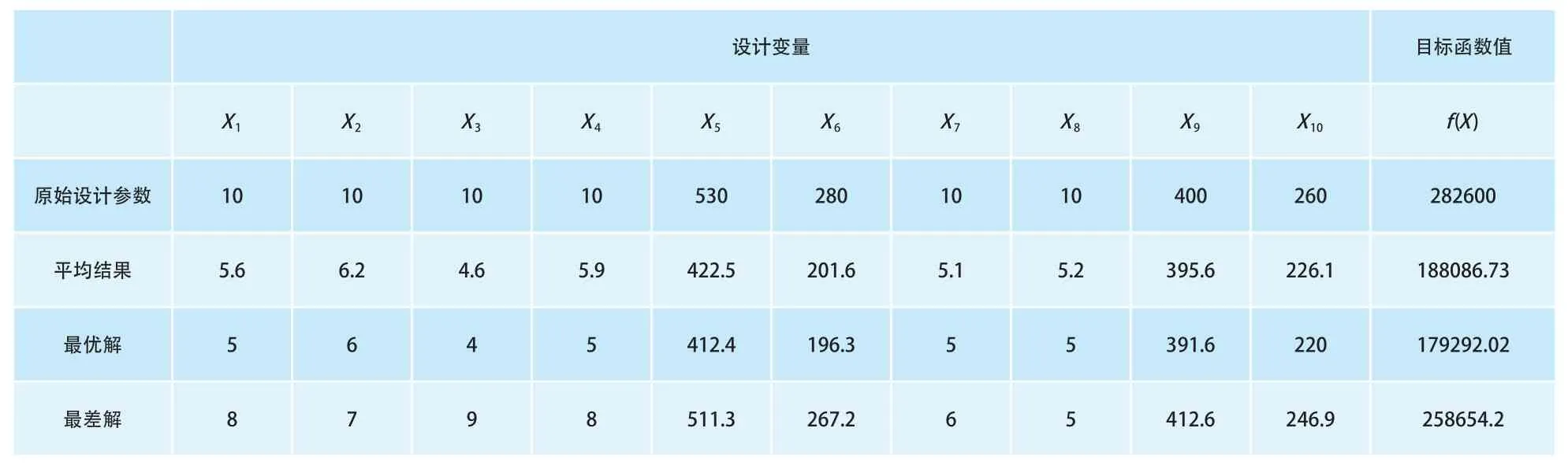
表2 优化计算结果

4 结论

本文提出了一种具有更快计算速度的全局FOA算法，结合Logistic混沌映射准则，利用混沌的遍历性和不确定性，在搜索空间混沌初始解，保证了算法计算起点的混沌性和全局性。根据当前果蝇个体的坐标，确定下一次迭代的搜索向量，保证了算法能够自适应的搜索更优解。通过对两个数值算例的分析及同传统FOA算法的比较，证明了本文改进方案的快速收敛及精度高的特性，将改进后的算法运用到通用桥式起重机金属结构的优化设计之中，对该算法解决实际问题的能力进行了验证。

［1］ 潘文超.最新演化式计算技术——果蝇优化算法［M］.台湾：沧海书局，2011.

［2］ Wang L.， Zhang X.L.， Wang S.Y.. A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem［J］.Knowledge-Based System，2013，48：17-23.

［3］ Li H.Z.， Guo S.， Li C.J.， et al.. A hybr id annual power load forecasting model based on generalized regression neural network with fruit fly optimiz ation algorithm［J］.Knowledge-Based System，2013，37：378-387.

［4］ Yuan Xiaofan， Dai Xiangshan， Zhao Jingyi， et al.. On a novel multi-swarm fruit fly optimization algorithm and its application［J］.Applied Mathematics and Computation，2014，233： 260-271.

［5］ 殷成凤.门座起重机人字架有限元分析［J］.建设机械技术与管理，2001（11）：24-25.

［6］ 谢光辉.机械优化问题的MATLAB求解方法［J］.煤炭技术，2001（9）：43-44.

［7］ 姜潮，张哲，韩旭，等. 一种基于论据理论的结构可靠性分析方法［J］.力学学报，2013，45（1）：103-114.

［8］ 邓亮，赵进，王新.基于遗传算法的网络编码优化［J］.软件学报，2008，19（8）：2269-2279.

The Improved FOA Algorithm Applied in the Shaft Bracket Structure Optimization Design Optimization Design

Liu Bin Jiang Huibo Wu Xiaolu
（Electrical Engineering of Jining vocational technical college Jining 272037）

In view of the poor global convergence ability of traditional Fruit Fly Optimization Algorithm（FOA algorithm）， and it is easily trapped in local minima， an improved FOA algorithm is proposed which has the function of chaotic mapping and cooperative co-evolution. Firstly， using the function of Logistic chaotic mapping for searching and initialize the drosophila population within the entire domain of convergence， to ensure the global computing ability of the algorithm， then taking advantage of the position of current flies to confirm the search direction and distance， so that the global computing ability of the algorithm can be confirmed. The improved algorithm is tested by two optimization function， the testing result shows that the algorithm has good global optimization ability. The successful application for the a-frame structure proves that the algorithm can be conducted to comprehensive promotion in the fi eld of mechanical optimization design.

FOA Logistic Co-evolution Optimization design

X941

B

1673-257X（2015）04-04-04

10.3969/j.issn.1673-257X.2015.04.002

刘彬（1980～），女，讲师，主要从事机械设计与制造工作。

2014-07-31）