采用有限差分求解高压直流输电线路空间离子流场的新方法

乔 骥 邹 军 袁建生 李本良

（1. 清华大学电力系统国家重点实验室 北京 100084 2. 国网北京经济技术研究院 北京 102209）

1 引言

直流电晕产生的离子会在输电线路空间形成离子流，该离子流在很大程度上影响输电线路的标称电场。计算空间离子流场和合成电场是分析直流输电线路电磁环境的基础。国外很早就针对高压直流输电线路电磁环境进行了大量的实验研究[1,2]，国内也对特定线路进行了电磁环境的测量[3,4]。

早在20世纪60、70年代，Sarma等人提出计算空间离子流场的一维模型，基于Deusth假设，认为空间离子流场只影响标称电场的大小，不影响其方向，为工程设计提供了大量的理论依据[5,6]。另外，有部分学者将理论计算与大量实验数据结合，给出计算电晕损耗的半经验公式[7]。到20世纪70年代末，由Janischewskyj等人提出有限元法计算空间离子流场[8]，之后又由更多学者进行了改进[9,10]。近些年国内各研究所和高校也进行了较为深入的研究[11-14]。总体来看，基于Deusth假设的研究引入了较多假设，计算精度较低，但计算速度相对较快；有限元等数值计算方法能够考虑较多因素，提高了计算精度，但计算效率较低。

本文采用 Sarma等人提出的模型进行仿真计算。该方法的基本思路是将求解离子流场的二维空间问题转化为沿电力线求解的一维问题，建立电力线弧长坐标系下的微分方程组及边界条件。求解该微分方程组的方法目前有两类。第一类是对微分方程组进行积分，求解离子浓度和合成场强的解析表达式。该方法计算速度快，但只适用于单极性空间离子流的求解，对于双极性空间离子流计算模型，无法得到解析解；第二类是通过优化方法求解微分方程组，该方法能够适用于单极性和双极性空间离子流计算，但是计算不易收敛。综合计算精度、计算效率及适用性的考虑，本文提出采用有限差分将微分方程组转化为非线性代数方程组进行求解。

2 空间离子流场与合成电场的计算原理

2.1 空间离子流场计算的数学模型

为便于说明，各符号含义如下：

E—— 空间合成电场强度（V/m）；

E′—— 空间标称电场强度（V/m）；

ξ—— 合成场强与标称场强幅值比；

Φ—— 合成电场电动势（V）；

φ—— 标称电场电动势（V）；

ρ—— 离子浓度（C/m3）；

ρ+,ρ-—— 正、负离子浓度（C/m3）；

J—— 离子流密度（A/m2）；

j+,j-—— 正、负离子流密度（A/m2）；

k—— 离子迁移率（m2/（V·s））；

k+,k-—— 正、负离子迁移率（m2/（V·s））；

ε0—— 真空介电常数（F/m）；

R—— 正、负离子复合速率系数（m3/s）；

U—— 导线运行电压（V）；

U0—— 导线起始电晕电压（V）；

Ec—— 导线起始电晕场强（V/m）；

Ec+,Ec-—— 正、负导线起始电晕场强（V/m）。

进行离子流场建模需要考虑以下几个方面进行数学描述：①泊松方程：电场由导线电荷及空间离子共同产生，用泊松方程描述空间合成场强；②电流密度方程：建立空间离子流密度与电荷浓度及合成场强的关系；③电流连续性方程：当离子流场达到稳态后，空间电场认为是恒定电场，电流满足连续性条件；④正负离子复合方程：对于双极性输电线路离子流计算模型，正负离子会发生复合反应，用复合方程进行数学描述。

基于上述方程，分别对单极性和双极性输电线路离子流场建立描述空间场量的方程组。

单极性空间离子流场数学模型

双极性空间离子流场数学模型

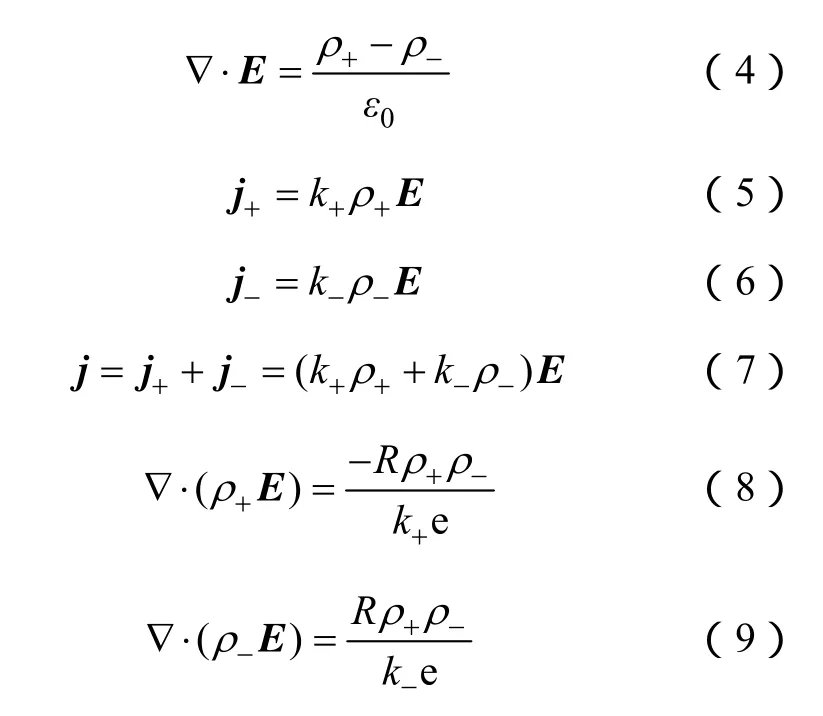
2.2 一维离子流场计算简化模型

为对上述数学模型进行简化，需引入以下基本假设：①Deutsch假设：空间中的带电离子只影响标称场强的幅值，不影响其方向；②Kaptzov假设：线路发生电晕后，线路表面的电场强度大小基本维持在起晕场强值不变；③离子运动模型简化：不考虑离子的扩散作用；认为离子迁移率为常数，采用离子迁移率的统计平均值；带电离子沿着标称电场的电力线运动，不发生偏移；不考虑风及空间悬浮颗粒对于离子运动的影响；④电离区简化：相对于线路空间的漂移区，电离区厚度可以忽略不计，认为电离区的边界与导线表面重合。

2.2.1单极性空间离子流场一维模型

以正极性输电线路空间离子流计算模型为例，如图1所示。

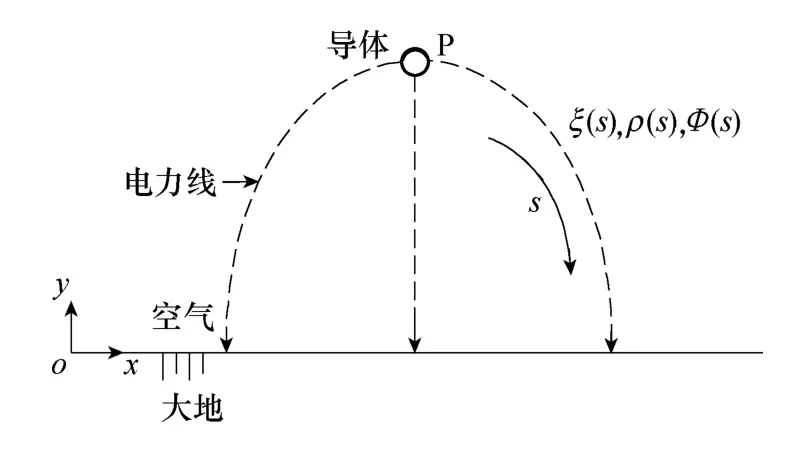
图1 单极性空间离子流计算模型示意图Fig.1 Calculation model of ion current in unipolar region

对于一条从正极性导线表面出发，终止于大地的电力线，以导线表面的电力线出发点作为坐标原点，沿电力线建立弧长坐标系，则电力线上的比例系数ξ、空间离子浓度ρ、合成电场电动势Φ以及合成电场场强E都可表示为弧长S的函数ξ(S)、ρ(S)、Φ(S)、E(S)。另外，在该电力线上，标称电场的电动势φ与弧长S具有一一对应的关系，因此比例系数ξ、空间离子浓度ρ、合成电场电动势Φ以及合成电场场强E也可表示为标称电场电动势的函数ξ(φ)、ρ(φ)、Φ(φ)、E(φ)。

建立沿电力线求解单极性离子流微分方程组

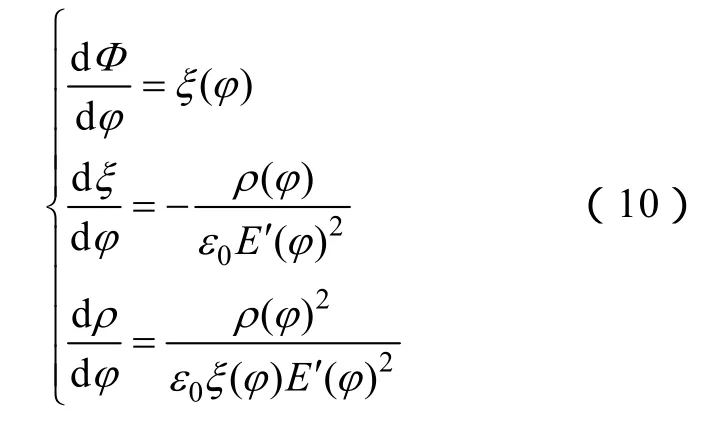
该计算模型的边界条件为

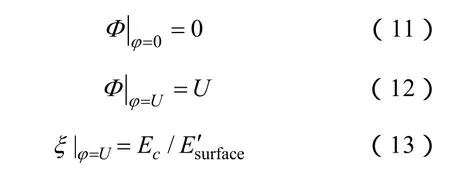
式（11）的含义为在大地或无限远处，标称电场和合成电场的电动势始终为零。式（12）的含义为在导体表面标称电场和合成电场电动势为线路的运行电压U。式（13）的含义为当导体表面发生电晕时，根据Kaptzov假设，导体表面的合成电场强度始终保持在起晕场强不变，此时的合成场强可由Peek公式直接给出。

2.2.2双极性空间离子流场一维模型

在分析双极输电线路的空间离子流场时，可将空间区域划分为两部分：单极性离子漂移区和双极性离子漂移区，如图2所示。

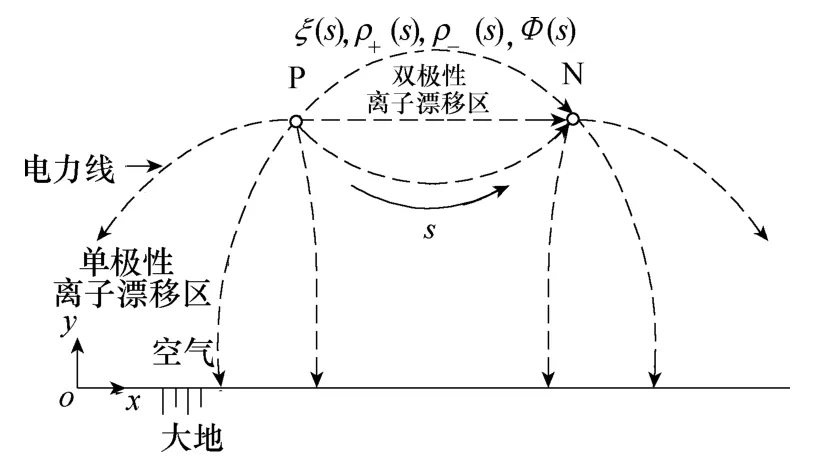
图2 双极性空间离子流计算模型示意图Fig.2 Calculation model of ion current in bipolar region

在单极性离子漂移区内，由于假设带电粒子始终沿电力线轨迹移动，因此从导线到大地或导线到无限远处的电力线上只存在单极性离子，仍可按单极性空间离子流计算模型进行分析；从正极性导线到负极性导线的电力线需要考虑双极性空间离子流场计算模型。建立沿电力线求解双极性空间离子流的微分方程组。

该计算模型的边界条件为

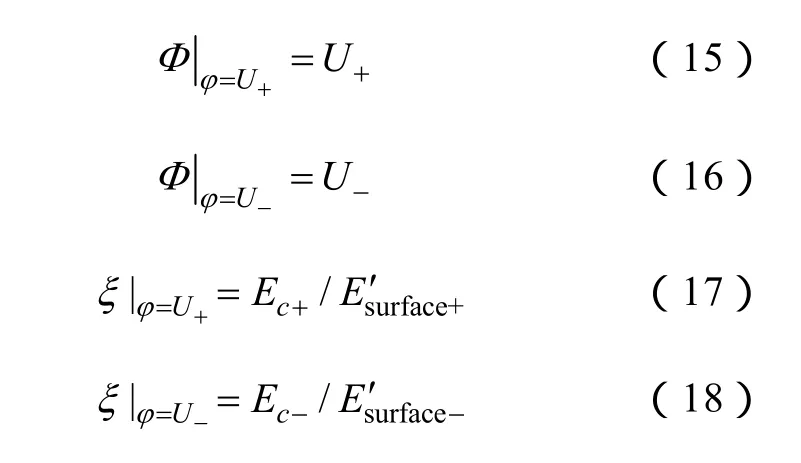
式（15）、式（16）的含义为在正、负极性导线表面，标称电场和合成电场的电动势为运行电压U+/-。式（17）、式（18）的含义为当导体表面发生电晕时，根据Kaptzov假设，导体表面的合成电场强度始终保持在起晕场强不变，此时的合成场强可由Peek公式直接给出。

3 有限差分求解空间离子流微分方程组

3.1 采用有限差分转化微分方程组的基本原理

在上述单极性和双极性空间离子流一维计算模型中，对于某一电力线，边界条件分别位于电力线的两端，因此构成了典型的两点边值问题。本文采用有限差分将原微分方程组转化为非线性代数方程组进行计算。以单极性空间离子流计算为例，其原理如图3所示。

对于从导线表面出发终止于大地的电力线，取其上的N个离散点。第一个点位于导线表面，第N个点位于大地，每个点的未知量设为ξn、ρn、Φn(n=1,2,3,…,N)。用离散点的有限差商近似代替微分，以前向差分公式为例，最终将原微分方程组转化为

图3 有限差分转换离子流微分方程组原理图Fig.3 Finite difference method to discrete the differential equations

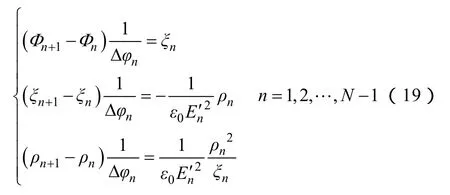
由边界条件得

N个离散点共有3N个未知数，式（19）、式（20）共建立了 3N个方程，且该方程组直接满足了边界条件。对于双极性空间离子流计算的微分方程组，也可采用类似的方法进行转换，不再赘述。

3.2 归一化差分方程

观察各未知量的数量级，对于实际工程的直流输电线路，Φ的数量级最大可达105V，ξ的数量级在100左右，ρ的数量级在10-9～10-7C/m3之间，数量级上相差非常大。如果采用最小二乘法原则求解该非线性代数方程，很可能会由于未知量数量级相差太多而使迭代过程无法收敛，无法找到最优解。本文采用的方法为将变量先进行归一化处理，使得求解的变量尽量保持在同一数量级，从而增加求解的准确度。

3.3 选取差分方程初值

计算非线性代数方程组时，需要给出待求解变量的初始迭代值。初值的选取极大影响迭代过程的收敛速度以及计算结果的准确度。本文采用的初值给定方法如下：

（1）对于变量Φn(n=1,2,3,…,N)，初值选取相应离散点的标称电场电动势φn(n=1,2,3,…,N)。

（2）对于变量ξn(n=1,2,3,…,N)，由于其值一般在1附近，所以选取初值为1。

（3）对于变量ρn(n=1,2,3,…,N)，在单极性空间离子流计算模型中，以ρm作为初值能够较好保证初值数量级在真值附近，ρm的计算公式由下式给出

对于双极性离子流计算模型，由于还没有相应的估算方法，而且其大小随线路几何参数和运行电压的变化而差别很大，因此先以离子浓度一般的数量级10-8C/m3作为初值，计算得到一组解，再利用该解估算相应数量级作为第二次计算的迭代初值，这样即可得到较为准确的解。

3.4 差分方法的取点方式及其收敛性

离散点的选取个数会直接影响方程的个数，而方程个数又影响求解的准确度及求解速度。假设已绘制的输电线路空间中某根电力线由N′个离散的绘制点拟合而成，即在该电力线的弧长坐标系上已有N′个离散点，在选取有限差分离散点时，可直接利用这些点求取。本文的取点原则为：

（1）导线附近电场强度变化速度较快，为了较准确描述导体表面附近的信息，需要选取较多的离散点。对于单极性离子流计算模型，先选取N′个离散点中离导线表面最近的N1=10个点；对于双极性离子流计算模型，分别选取电力线上离正、负极性导线表面最近的N1=10个点，共 2N1=20个点。

（2）剩余的N′-N1个离散点中，根据相邻离散点标称电动势差相等原则选取N2个点，该N2个点的弧长坐标、标称电场强度以及标称电场电动势根据N′-N1个离散点的数据，采用插值方式进行计算。

图 4为葛-上线单回双极四分裂输电线路地面离子流的计算结果。其中N2分别取 10、20、30、40。可以看出，随着离散点数的增加，计算结果逐渐收敛。当N2增大到20后，随着离散点数的增加，计算结果的变化已经不明显。因此，可以认为N2=20时，计算结果已经较为准确。线路参数：导线高度H=12.5m，极间距离D=14m，导线半径r=1.185cm，分裂间距s=0.45m，运行电压U=±500kV。

图4N2不同时地面离子流计算比较Fig.4 Comparison of ion current density on the ground level with differentN2

表1为单极性离子流模型中N2取不同值时计算单根电力线离子流的平均时间。综合考虑计算精度和计算时间，最终N2的取值为20。

表1N2取不同值时计算单根电力线离子流的时间Tab.1 Computing time of space charge density on one flux line with differentN2

（3）由于按照等电动势差的原则选取N2个点，这会导致在电场强度幅值较小的位置选取的离散点之间的弧长距离过大，影响计算精度。因此需在弧长间距过大的两离散点之间插入新的离散点。

3.5 有限差分计算方法验证

为验证有限差分计算方法的正确性，与文献[6,12]比较单极性和双极性空间离子流计算结果。文献[12]采用积分解析法进行葛-上线地面离子流以及合成场强的求解，计算结果比较如图5a、5b。文献[6]给出了双极性输电线路，两极之间的一根电力线的双极性离子浓度计算结果，比较结果如图6线路参数为：极间距离D=10.36m，导线半径r=1.02cm，运行电压U=±350kV。

图5 单极模型有限差分法计算结果与文献结果比较Fig.5 Comparison between the results of proposed method and previous ones in unipolar region

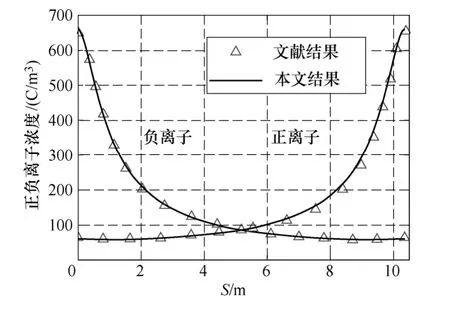
图6 双极模型有限差分法计算结果与文献结果比较Fig.6 Comparison between the results of proposed method and previous ones in bipolar region

表2为不同方法计算单回输电线路全空间离子流场的用时。可以看出，对于单极性和双极性空间离子流模型的计算，本文方法的用时分别是优化方法的4.25%和2.6%，该方法大幅提高了计算速度。

表2 不同方法求解离子流场用时比较Tab.2 Computing time using different methods

4 双回直流输电线路离子流计算举例

采用本文方法计算双回水平排布和纵向排布直流输电线路地面离子流场及合成电场。线路排布如图7、8所示，计算结果如图9、10所示。

图7 双回水平排布直流输电线路排布结构Fig.7 Geometric configuration of a double-circuit DC transmission line

图8 双回纵向排布直流输电线路排布结构Fig.8 Geometric configuration of a double-circuit DC transmission line

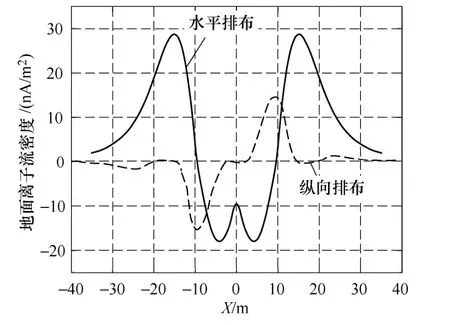
图9 双回直流输电线路地面离子流Fig.9 Ion current density on the ground level of the double-circuit DC transmission line

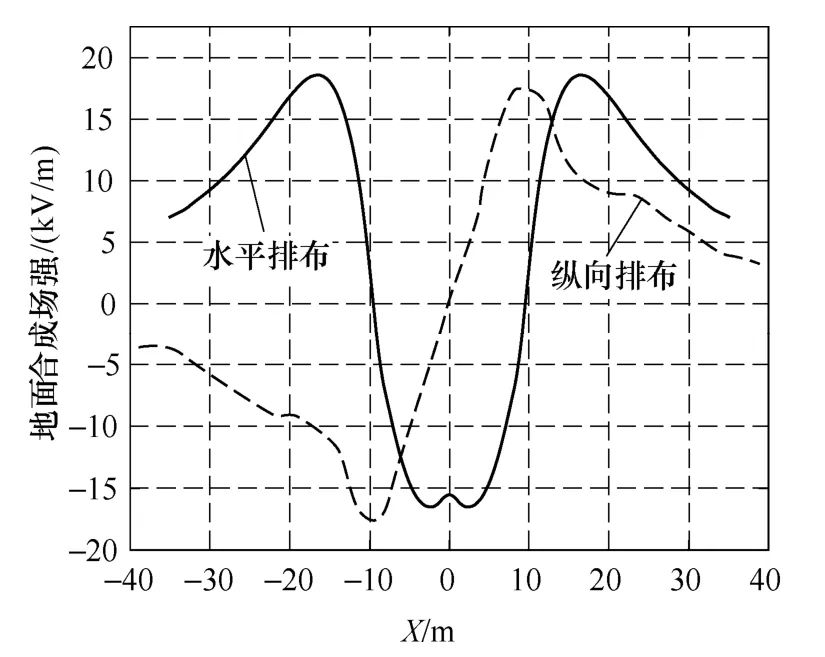
图10 双回直流输电线路地面合成场强Fig.10 Total electric field on the ground level of the double-circuit DC transmission line

另外，本文计算了双回输电线路空间离子流场分布。结果显示水平排布方式空间离子浓度最大值约为2.5×10-6C/m3，纵向排布方式空间离子浓度最大值约为4×10-7C/m3，水平排布的整个空间离子浓度比纵向排布高一数量级。与水平排布方式相比，纵向排布对于限制地面最大合成场强并没有优势，但其可以有效降低线路外侧的合成场强大小，节约线路占地面积。从限制地面离子流和合成场强的角度考虑，双回直流输电线路应采用纵向排布方式。

5 结论

本文提出采用有限差分方法计算直流输电线路空间离子流场及合成电场，该方法直接满足边界条件，降低了方程求解难度，有效提高了计算速度，并且能够适用于任意回数的单、双极直流输电线路空间离子流场的求解。对于差分方程的建立与求解，本文针对方程的归一化方法、初值选取以及取点方式给出了一定的参考原则。基于本文方法，计算了双回直流输电线路的地面离子流场与合成电场。结果显示双回直流输电线路应采用纵向排布方式。

[1] Morris R M, Morse A R, Griffin J P, et al. The corona and radio interference performance of the nelson river HVDC transmission lines[J]. IEEE Transactions on Power Apparatus and Systems, 1979, (6): 1924-1936.

[2] Dallaire R D, Maruvada P S. Corona performance of a±450kV bipolar DC transmission line configuration[J]. IEEE Transactions on Power Delivery, 1987, 2(2):477-485.

[3] 李敏, 余占清, 曾嵘, 等. 高海拔±800kV直流输电线路电磁环境测量[J]. 南方电网技术, 2011, 5(1):42-45.

Li Min, Yu Zhanqing, Zeng Rong, et al. Electromagnetic environment measurement of ±800kV DC transmission lines at high altitude[J]. Southern Power System Technology, 2011, 5(1): 42-45.

[4] 傅宾兰. 葛南直流输电线路单极运行的电晕损失[J].电网技术, 1993, 17(3): 004.

Fu Binlan. Monopolar corona loss of Gezhouba-Nanqiao HVDC transmission line[J]. Power System Technology, 1993, 17(3): 004.

[5] Sarma M P, Janischewskyj W. Analysis of corona losses on DC transmission lines: I-unipolar lines[J].IEEE Transactions on Power Apparatus and Systems,1969(5): 718-731.

[6] Sarma M P, Janischewskyj W. Analysis of corona losses on DC transmission lines part II-bipolar lines[J]. IEEE Transactions on Power Apparatus and Systems, 1969(10): 1476-1491.

[7] Corbellini U, Pelacchi P. Corona losses in HVDC bipolar lines[J]. IEEE Transactions on Power Delivery,1996, 11(3): 1475-1481.

[8] Janischewskyj W, Cela G. Finite element solution for electric fields of coronating DC transmission lines[J].IEEE Transactions on Power Apparatus and Systems,1979(3): 1000-1012.

[9] Lu T, Feng H, Cui X, et al. Analysis of the ionized field under HVDC transmission lines in the presence of wind based on upstream finite element method[J].IEEE Transactions on Magnetics, 2010, 46(8): 2939-2942.

[10] 袁海燕, 傅正财. 基于有限元法的±800kV 特高压直流输电线路离子流场计算[J]. 电工技术学报,2010, 25(2): 139-146.

Yuan Haiyan, Fu Zhengcai. Corona ionized field analysis of ±800kV HVDC transmission lines[J].Transactions of China Electrotechnical Society, 2010,25(2): 139-146.

[11] Li W, Zhang B, Zeng R, et al. Discussion on the deutsch assumption in the calculation of ion-flow field under HVDC bipolar transmission lines[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2759-2767.

[12] 傅宾兰. 高压直流输电线路地面合成场强与离子流密度的计算[J]. 中国电机工程学报, 1987, 7(5): 56-63.

Fu Binlan. Calculation of electric field and ion current density for bipolar HVDC line[J]. Proceedings of the CSEE, 1987, 7(5): 56-63.

[13] 李乐霞. 起晕电压值对直流输电线路下地面合成场强的影响分析[J]. 电气应用, 2012(16): 64-67.

Li Yuexiang. Effect of onset voltage on the total electric field on the ground level of HVDC lines[J].Electrotechnical Application, 2012(16): 64-67.

[14] 李永明, 邹岸新, 徐禄文, 等. 特高压直流输电线路离子流场的有限元-积分法计算[J]. 高电压技术,2012, 38(6): 1428-1435.

Li Yongming, Zou Anxin, Xu Luwen, et al. Calculation on corona ionized field of UHVDC transmission lines by finite element-integral method[J]. High Voltage Engineering, 2012, 38(6): 1428-1435.