基于效用风险熵权模糊综合评判的复杂电网节点脆弱性评估

丁 明 过 羿 张晶晶 钱宇骋 齐先军 何 剑 易 俊

（1. 合肥工业大学电气与自动化工程学院 合肥 230009 2. 中国电力科学研究院 北京 100192）

1 引言

电力系统节点是能量传输的出发点和重要汇聚地，如果由于战争[1]、蓄意破坏[2]或严重自然灾害[3]造成节点被破坏或退出运行，将会对电力系统安全运行产生直接影响。因此，节点的脆弱性评估一直是电力学术界和工程界关注的问题。

在对电网复杂网络特性的研究中，节点的重要性通过节点在电网中的位置信息和连接方式进行描述，通常采用度数和介数等指标衡量节点重要性。节点的脆弱性定义为从网络中有选择地移除某个节点所造成的网络性能下降的程度，通常采用系统连通性水平、网络效率和最大传输能力等指标衡量节点脆弱性。这两种评价体系从不同的角度描述了复杂网络的特性，不完全等效但有一定联系。文献[4]指出在电力系统复杂网络特征模型下，电网元件的重要性能够以一定概率辨识元件的脆弱性，并且，较之元件脆弱性分析，元件重要性分析具有良好的计算性能。本文试图从节点的复杂网络特征（即节点的重要性）角度出发进一步探讨电网节点的脆弱性。

从复杂网络角度发掘电网关键节点的方法可以分为两类[5]：一类是社会网络分析方法，另一类是系统科学分析方法。前者所涉及的指标主要用于评价电网节点的重要性，后者所涉及的指标则侧重于衡量电网节点的脆弱性。

社会网络分析方法的核心思想是“重要性等价于显著性”，对网络中重要节点的发掘以不破坏网络的整体性为基础，在分析中保留了原网络拓扑结构，一般采用节点中心性指标，如度中心性、介数中心性和接近中心性等指标。文献[6]指出网络中度指标较高的节点在蓄意攻击下较脆弱；文献[7,8]采用介数指标来衡量元件在网络中的关键程度，指出节点被网络中所有发电机-负荷节点之间最短路径经过的次数越多，该节点越重要，且介数指标较度数指标能更好地辨识电网的脆弱环节；文献[9]提出以节点“结构负荷”，即加权介数来辨识关键节点；文献[10]提出节点电气介数，基于基尔霍夫定律，克服了加权介数模型假设条件中存在的不足；文献[11-13]定义母线输电介数，采用功率分布因子表示节点注入对支路功率的影响，但忽略了电力系统功率供需平衡的特点。

系统科学分析方法的核心思想是“脆弱性等价于该节点被删除后对网络的破坏性”，删除某节点后，可借助网络连通性指标的变化来确定该节点的脆弱程度，在分析中改变了原拓扑结构，常采用的指标是生成树、网络凝聚度和以失负荷比例为代表的脆弱性指标。文献[14-16]采用节点收缩后的网络凝聚度对电网关键节点进行辨识，综合考虑了节点度数和节点在网络中的位置信息，所存在的问题是如果不同节点收缩后网络拓扑结构相同，这些节点也处于同等地位，因而不易区分。文献[17]采用节点退出运行后的最小失负荷百分比辨识脆弱节点，但未考虑系统的电压和无功等因素。

目前基于复杂网络特征的节点脆弱性评估指标从不同的角度描述节点在特定电网中的脆弱性，采用单一指标针对不同电网拓扑下的节点脆弱性评估具有较大的片面性。针对上述问题，本文提出了基于效用风险熵权和模糊综合评判的节点脆弱性评估模型。研究工作分为5步：①定义了效用风险熵和节点的效用风险熵权，综合节点脆弱性指标集合中的客观数据信息和节点的价值系数，形成客观权重；②通过层次分析法，将专家主观判断转化为定量主观权重；③将上述两种权重以合理方式结合形成综合权重，适用于具有不同运行经验的电力系统；④建立了基于模糊综合评判的节点脆弱性评估模型，将节点按脆弱性大小进行排序并按脆弱性等级分类；⑤给出了算例结果和讨论。

2 权重的确定方法

2.1 效用风险熵权的确定

以往的熵权决策理论中熵的定义[18]是在事件概率分布空间内的总体平均测度函数，称之为概率风险熵。对电网脆弱性进行辨识时，系统或元件的风险不仅与脆弱元件的概率分布有关，还与其退出运行造成的结果价值分布有关。对于复杂电网节点脆弱性评估，需要结合风险函数对熵的内涵加以丰富，使之能全面反映节点所面临的脆弱性。

定义1 效用风险熵。事件空间中的事件Si（i=1,2,…,n）是以概率Pi出现的随机事件，将事件Si对系统产生的事故后果Ci定义为事件Si对系统的价值系数，相同指标体系下Ci只具有相对意义。将事件的价值系数和其概率分布的归一化值定义为事件Si的效用系数

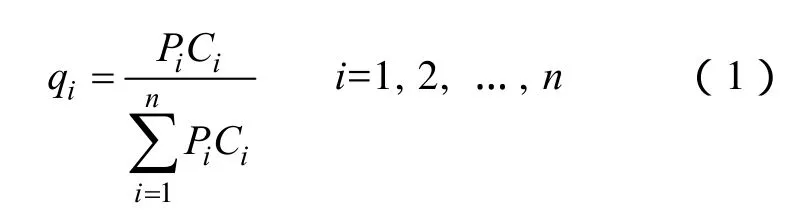
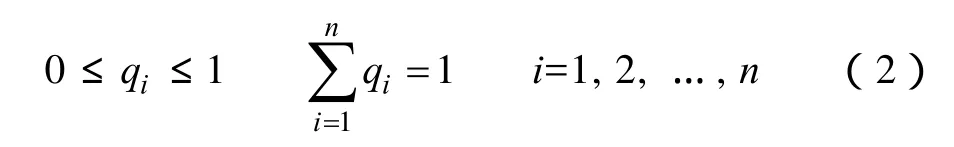
把概率空间中事件的风险函数在效用系数空间中的平均值定义为系统的效用风险熵，即

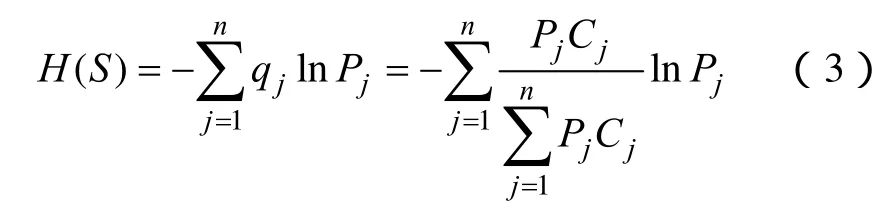
效用风险熵是复杂系统总体风险的统计平均值，它取决于系统各事件的概率分布和价值系数空间的总体结构，符合总体测度函数的基本条件。其衡量的并不是系统面临的风险大小，而是系统风险的总体不确定性，即系统崩溃可能的不确定性的测度，反映对系统风险的总体预测和把握的能力[19]。

在下文中，节点指标集合中的各指标反映节点脆弱性在不同评价角度下的概率不确定性。节点的价值系数以停电规模表示，即该节点退出运行后被切除负荷与负荷总需求的比值。文中通过优化算法来计算节点退出运行而导致的停电规模。本模型中采用直流优化潮流，计算步骤如下：

（1）将节点退出运行。

（2）线路过载则断开，计算潮流，检查是否有线路过载。

（3）在功率平衡约束、发电机出力约束、负荷约束和线路容量约束下求取优化结果，优化目标为切负荷量最小。

（4）统计切负荷量，计算停电规模。

将电网节点看成方案，节点脆弱性评估指标看成节点所具有的属性。设电网有m个节点，各节点包含脆弱性指标n个，则对应的决策方案集合中有m个方案，每个方案有n个属性。节点i的第j个指标值记为ijr'，构成决策矩阵 'R。

不同评估指标的量纲可能不同，这样就不具可比性，应该对该决策矩阵进行标准化处理。评价指标分为效益型和成本型两类。效益型指标值越大越好，成本型指标值越小越好。对决策矩阵做如下标准化处理

定义2 效用风险熵权。根据定义1，第j个指标的效用风险熵为

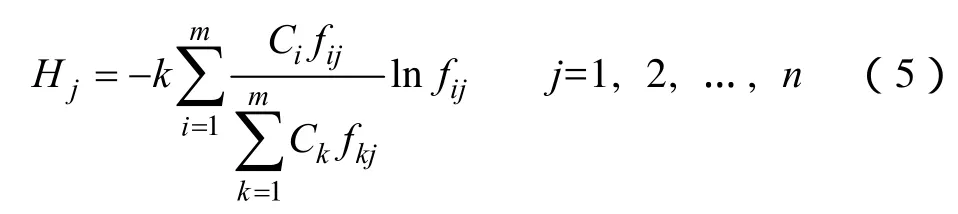
式中，k=1/lnm，，Ci为节点i退出运行导致的停电规模，即价值系数；0＜Hj＜1，且当fij=0时，规定 lnfij=0。相应地，第j个指标的效用风险熵权定义为

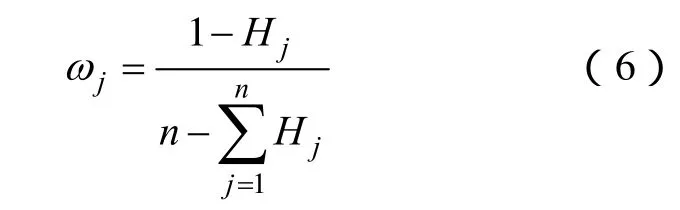
式中，0≤ωj≤1，且。

由上述定义可看出，某指标的效用风险熵权越大，表示该指标能凸显各节点的差异，越能为最终的决策提供更多的有用信息；若效用风险熵权为0，则该指标的效用风险熵值达到最大值 1，各节点在该指标上的取值完全相同，表明该指标未向决策者提供任何有用信息，可以被剔除。

2.2 专家权重的确定

熵权所反映的是客观数据所蕴含的信息，但是这种客观性仅反映了该指标在评估中所能提供有效信息的多少，即节点之间的差异性，并不反映该指标对实际问题的重要程度，还需要专家根据自己的偏好及实际运行经验进行决策。

本文采用层次分析法（Analysis Hierarchy Process，AHP）将专家决策过程中的定性和定量因素有机结合起来，步骤如下：

（1）采用三标度法（0,1,2）对指标进行两两比较后，构建比较矩阵B，0～2标度的判断尺度量化规则见表1。

表1 判断尺度量化规则Tab.1 Quantification rule of judgment criterion

（2）将比较矩阵转化为判断矩阵，并通过验证一致性保证数据可信度，最后确定各指标权重。

形成比较矩阵时，通常采用三标度法或九标度法进行专家评分。当专家评分时，若采用过多的标度来衡量指标的优劣，很难掌握标度的标准，做出的判断往往不能满足一致性检验。在咨询过程中采用三标度法时，专家很容易做出判断，既能满足一致性又能使特征值的计算量大大减少，从而使AHP法易于被决策者接受。

2.3 综合权重的确定

评估既要充分提取客观数据蕴含的信息，又要充分尊重专家的主观意见，这就要求效用风险熵权与专家权重以合理的方式结合。综合权重的生成往往通过客观权重和主观权重以同等地位参与综合权重的确定过程，并没考虑两种权重在不同条件下的主次问题。设n个指标的专家主观权重为e=（e1，e2，…，en），综合权重表示为

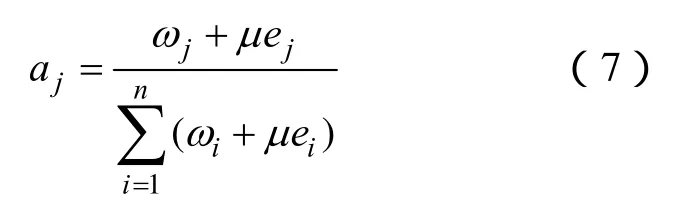
式中，aj为指标j的综合权重；μ为专家权重相对效用风险熵权的比例系数，取值范围为 0.3＜μ＜3。当μ取 1时，表示专家权重与效用风险熵权以相同的权重参与综合权重中。

3 节点脆弱性综合评估指标集

对本文所采用的4个指标给出以下定义，其中网络凝聚度指标和介数指标定义在电网无权网络模型中，脆弱性贡献指标定义在以线路电抗为边权的电网加权模型中，节点对间的最短路径定义为两节点间所有路径中线路权重和最小的路径。

定义 3 节点度指标I1。节点度指标是指连接该节点的边数。节点度指标定义表明节点与其他节点直接通信的能力，考虑的主要是节点本身的位置信息，节点度值越大，在网络中越重要。

定义 4 网络凝聚度指标I2。定义节点（集）收缩后的网络凝聚度值为被收缩节点（集）的重要度

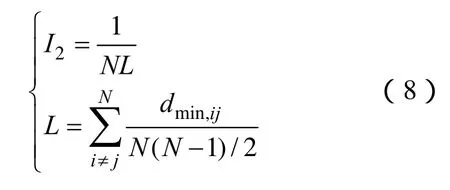
式中，N为网络中的节点数目；L为节点之间的平均最短路径；dmin,ij为电网中任意两节点i和j间的最短路径。网络凝聚度指标反映的同样是节点（集）的位置信息，节点网络凝聚度值越大，在网络中越重要。若节点收缩后拓扑结构一致，则节点具有相同的重要度。

定义 5 节点介数指标I3。节点介数[8]是指节点被网络中所有发电机节点与负荷节点之间最短路径经过的次数。节点介数指标认为，若节点是电网中发电机节点和负荷节点间最短路径的必经之路，则节点在网络中具有对应的重要程度。节点介数指标越大，在网络中越重要。

定义 6 节点脆弱性贡献指标I4。节点脆弱性与其在网络中所处的位置及相邻节点的作用密切相关。节点脆弱性评估可以从节点对网络资源掌控能力的角度，综合考虑节点自身在网络中所处位置和相邻节点对该节点的脆弱性贡献情况。节点脆弱性越高，节点遭受蓄意攻击的可能性就越大。

节点的位置信息即全局脆弱性可以通过节点的效率值进行描述。节点的效率值可以通过该节点到达其他节点的难易程度进行量化，体现该节点对网络资源控制能力，即对网络资源传输做的贡献。节点的效率值越大，该节点在网络资源传输过程中所处的位置越重要，该节点遭到攻击导致网络资源传输能力大幅降低的可能性也越大。节点i的效率值，即节点的全局脆弱性EGi定义为

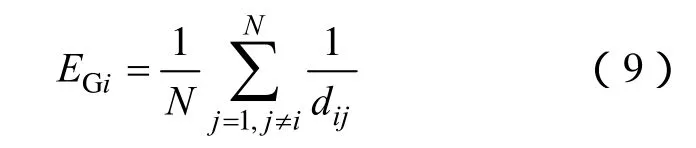
式中，N为节点数；dij为节点i到j的最短路径。

节点间最主要的脆弱性贡献传递关系体现在相邻节点间。节点对其相邻节点的脆弱性贡献与节点自身的度值和效率值有关，效率值越高、度值越大，可以认为该节点对相邻节点的脆弱性贡献作用越明显。为区分不同节点间脆弱性贡献关系的强弱，在节点脆弱性贡献值中融合节点的全局脆弱性。节点j对节点i局部脆弱性贡献值为

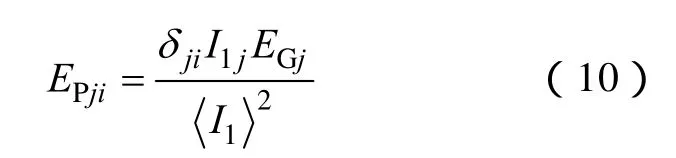
通过节点的全局脆弱性和相邻节点对其的脆弱性贡献，定义节点i的脆弱性

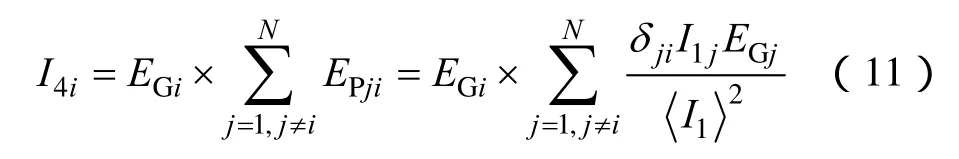
用上式表示节点脆弱性综合了节点的全局脆弱性和局部脆弱性，较完整地反映了节点对网络资源的控制能力，符合节点脆弱性评估的实际需求。

在运用上述指标识别出脆弱节点后，还需要对所筛选出的电网脆弱节点进行验证。本文引入输电能力下降指标[20]来衡量故障传播的程度，定义为节点间阻抗倒数的和，即

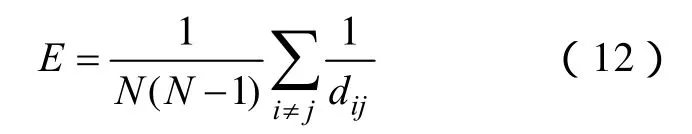
输电能力百分比表示为

式中，E0和E1分别为初始状态下和故障后电网的输电能力。计算过程是：针对基于不同方法获得的脆弱节点排序表，由高至低对节点采取静态攻击[21]；一旦这些节点受到攻击，将不再恢复运行，重新计算输电能力下降指标，其大小可以作为对节点脆弱排序的对比验证。输电能力下降越多，说明节点故障对系统造成的影响越大，节点越脆弱，在基于复杂网络理论的电网拓扑特征研究中，采用输电能力百分比衡量故障传播深度得到了广泛认可。

可以看出，不同指标从不同的角度探讨了节点在复杂电网中的重要程度，但对于实际电网，仅依赖站在某一角度考虑的指标（集）来评估节点在电网中的脆弱性具有较大的片面性。本文综合这些指标，提出一种基于效用风险熵权的多属性模糊决策方法对复杂电网节点脆弱性进行评估。

4 模糊综合评判方法

4.1 备择集与隶属函数的选取

备择集是评判者对评判对象可能做出的各种总的评判结果组成的集合。第2节中规范化后的决策矩阵将各节点的指标变换到相应的论域范围，使其能均匀分布于[0,1]内。对节点指标集进行模糊分割，模糊空间的分级数即备择集中评判结果的个数决定了模糊综合的精细化程度，脆弱性备择集的划分需满足隶属函数论域上模糊集的对称和平衡。本文将备择集中评判结果按脆弱程度划分为5个等级V={v1，v2，v3，v4，v5}={极低（1 级）、低（2 级）、中等（3级）、高（4级）、极高（5级）}。

若节点脆弱性指标属于定性描述，隶属函数为半梯形分布；若属于定量指标，隶属函数为三角形或正态型分布。本文将定性分析和定量分析相结合，但对于节点脆弱性评估而言，所要获得的结论是节点间相对重要性的定量结果。考虑备择集的划分，取等腰三角形隶属函数构造评估所需要的隶属函数，如图 1所示。其中，pk、qk及sk分别为当前脆弱程度下的分布参数，见表 2。这样可以保证节点脆弱性指标模糊综合的精细化程度，令每个指标至少得到4个备择集中的不同元素的隶属度。

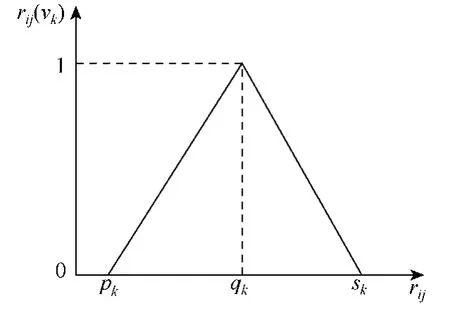
图1 脆弱性的隶属度分布规律Fig.1 Distributions of vulnerability membership degree

表2 等腰三角形分布的参数设置Tab.2 Parameter settings of isosceles triangle distributions

4.2 模糊评价矩阵与综合评价模糊子集

本文节点脆弱性评估模型的核心有两个：一是寻找合理的综合权重表达式，二是寻找规范化后的决策矩阵到脆弱性备择集的合理映射。由 3.1节可得关于4种不同类型节点脆弱性指标的模糊综合评价矩阵Ri。设综合权重向量为A=(a1,a2,a3,a4)。节点i的综合评价模糊子集为

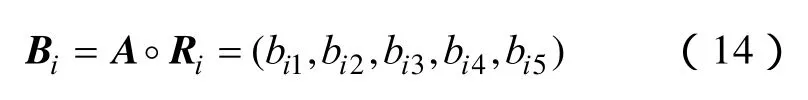
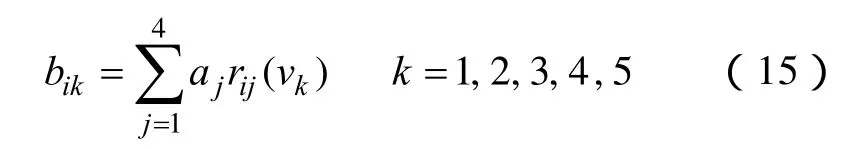
这种模型不仅考虑了节点中所有指标的影响，而且保留了单个指标的评判信息，在研究工程问题时应用较多。

对Bi进行归一化处理

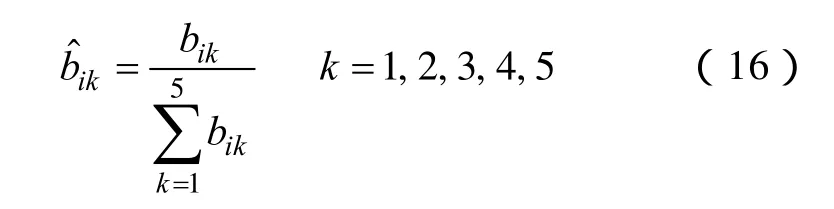
节点i的模糊综合评价结果为

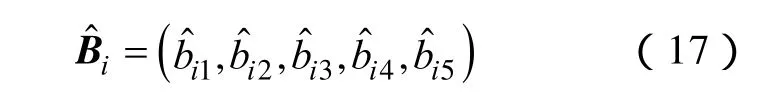
4.3 综合评价指标的排序

各节点的模糊综合评价结果提供了节点指标的全面信息，利用其对电网节点脆弱性进行分类和排序，本文采用如下三种方法：

（1）最大隶属度法。用各节点模糊综合评价结果中最大隶属度值对应的备择集元素来描述节点脆弱程度，对节点按脆弱等级分类。需要注意，最大隶属度法对不同节点的模糊综合评价结果体现出不同的有效性，定义采用最大隶属度法描述节点脆弱性的有效性系数为

式中，n为备择集中元素个数；β和γ分别为模糊综合评价结果中的最大隶属度和次大隶属度。若α=+∞，此方法对该节点完全有效；若1≤α＜+∞，此方法对该节点非常有效；若 0.1≤α＜1，此方法对该节点较有效；若 0＜α＜0.1，此方法对该节点效果较差；若α=0，此方法对该节点失效。

（2）最优评价法。按各节点模糊综合评价结果中对应备择集第5级元素的隶属度值进行排序，若出现节点第5级隶属度值相同的情况，则按第4级元素的隶属度值进行排序，依此类推。

（3）综合得分法。给脆弱性备择集元素赋予具体分值，将定性描述转化为定量描述，定量描述的脆弱性备择集为60、70、80、90}。节点i的得分为，按节点得分高低，将节点按脆弱性由大到小排序。

采用基于效用风险熵权模糊综合评判的电网节点脆弱性评估模型可实现节点脆弱性的多个方案的完全排序和分类。

5 算例验证

5.1 节点脆弱性评估指标权重的求取

本文采用IEEE 39节点系统作为测试系统，如图2所示。

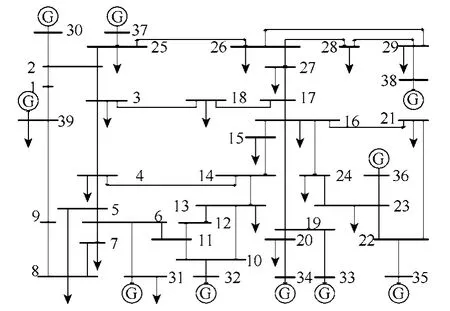
图2 IEEE 39节点系统接线图Fig.2 Connection diagram of IEEE 39-bus system

按照第2节中指标定义分别计算4种类型的节点指标，采用基于直流潮流的优化模型计算各节点退出运行造成的价值系数。各指标的效用风险熵和效用风险熵权见表3。

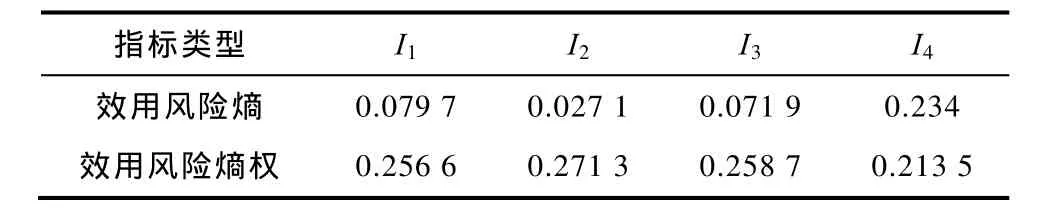
表3 各指标的效用风险熵和效用风险熵权Tab.3 Effect risk entropies and effect risk entropy weights of the indices

从表3可看出，各指标的效用风险熵和效用风险熵权呈反比关系，效用风险熵越大，相应的效用风险熵权越小。需要说明，指标I4的效用风险熵权相比其他三类指标较小，说明该指标相对其他指标在竞争意义上的相对重要程度较低，但并不表示该指标的实际重要程度。

在求节点各指标专家权重时，采用AHP法，首先构建基于三标度法的比较矩阵，见表4。

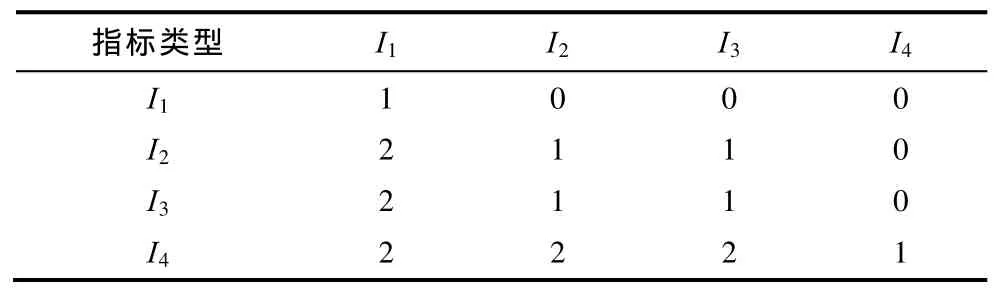
表4 基于三标度法的比较矩阵Tab.4 Comparison matrix based on three-hierarchy AHP method

比较矩阵B的构建考虑以下因素：①节点度指标值反映网络中节点的基本位置信息，涉及的结构因素最少，故和其他指标相比相对重要性较差；②网络凝聚度和节点介数考虑的都是节点的全局重要性，并未考虑相邻节点脆弱性的贡献情况，故两者在节点脆弱性评估中重要性处于同一水平；③节点脆弱性贡献指标综合考虑了节点的全局和局部脆弱性，相对前3个指标重要。

将比较矩阵用极差法构造判断矩阵，按一致性指标验证，得到专家权重指标，见表5。

表5 各指标专家权重Tab.5 Expert weights of the indices

从表5可以看出，表4中信息通过层次分析法将对节点指标相对重要性的主观定性评价转化为定量分析，为主观定性信息与客观定量信息的结合提供了接口。

在综合权重求解中，比例系数μ=1，表示两种权重以同等地位参与综合权重的构成，各指标的综合权重见表6。

表6 各指标综合权重Tab.6 Integrated weights of the indices

从表6可以看出，综合权重结合了对节点指标的主观经验和节点实际指标的客观信息，有效融合了效用风险熵权重和专家权重。实际上，对于不同的电力系统，可以根据运行人员的长期经验进行权重的选择。若某类指标分析结果与从电网结构的长远统计角度所得结果一致性较高，则可采用专家权重进行决策；在很多电网网络规划缺乏足够实际运行状态数据情况下，则可综合主客观权重或单独采用客观权重进行决策。

5.2 节点脆弱性分析

按节点脆弱性指标集合中4种指标分别计算节点脆弱性值。由此得出在不同权重下的节点脆弱性分布，排序1和排序2分别表示节点脆弱性按最优评价法和综合得分法进行排序，见表7。

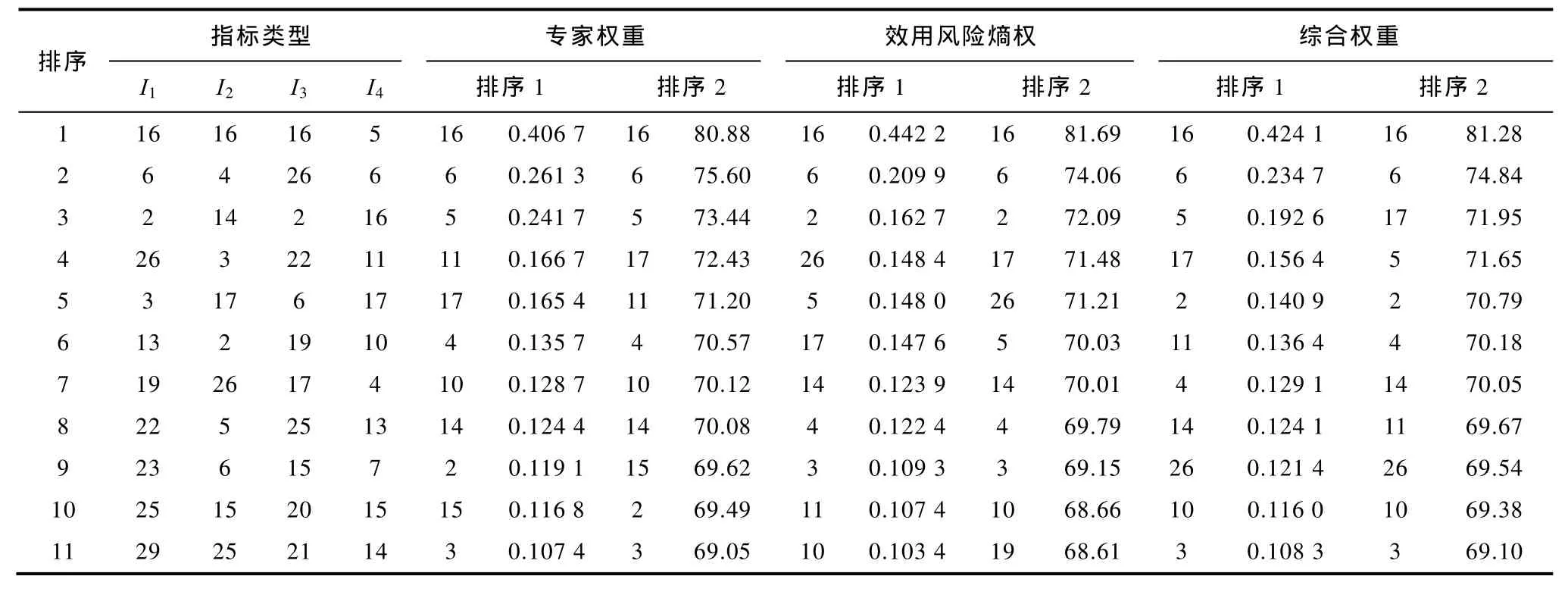
表7 节点脆弱性排序Tab.7 Vulnerability identification results of nodes

从表7可以看出，4种指标评估结果不尽相同，原因在于各种指标或是基于社会网络的方法或是基于系统科学的方法，都是从特定角度对节点的脆弱性进行关注。如节点4在度指标和介数指标中都不能得到较好反映，但从网络拓扑结构可以发现，其传输通道比较单一，节点退出运行后对其他节点和支路的冲击比较集中，本文指标体现了4种单一指标的互补性，较好反映了节点4的脆弱性。网络凝聚度指标排序与本文指标具有一定相似性，但注意到，网络凝聚度指标中排名靠前的节点4和14，节点收缩后的网络拓扑一致，导致两节点网络凝聚度值相同，并不能较好地反映节点脆弱性的差异性。脆弱性贡献指标综合考虑了节点的全局和局部脆弱性，与本文指标较为贴近，但其仍属于社会网络类分析方法，并未从实质上摆脱脆弱性评估时可能存在的信息片面性的问题。

三种权重下的脆弱性评估结果则综合考虑了特定指标体系下的网络特征。专家权重通过专家意见将定性经验转化为定量描述，通过各指标权重间相对重要性的对比分析，给出含主观信息的脆弱性评估结论；效用风险熵权通过综合节点脆弱性的概率不确定性和节点退出运行的价值系数，给出含客观信息的脆弱性评估结论；综合权重通过主观权重和客观权重以合理方式组合，实现节点数据信息与专家主观偏好的良好结合。3种权重下的节点脆弱性在脆弱节点评估结果上具有良好的一致性，如节点16、17和14，与这些节点相连的线路均处于重要输电通道上，这些节点退出运行对系统稳定性影响较大。以与节点16相连的线路为例说明，支路16-17断开将导致节点18和节点27的功率不平衡，由此可能引发包括功角稳定等一系列问题，支路 16-19是发电机33和34向电网输送功率的唯一通道，其断开将造成系统解列。

为验证上述节点脆弱性指标能有效辨识脆弱节点，按第3节所述方法，在六种不同的攻击模式下连续攻击脆弱性较高的6个节点，计算被攻击后系统的输电能力百分比，如图3所示。

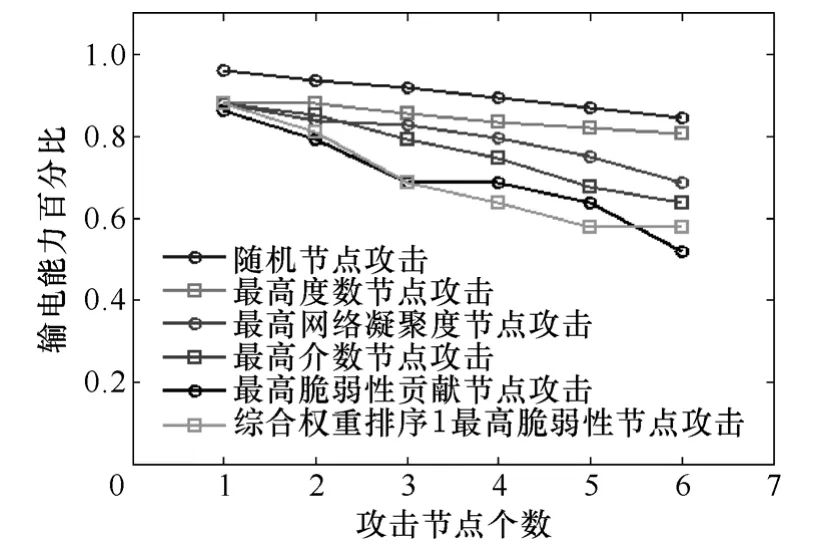
图3 不同攻击模式下的输电能力百分比变化Fig.3 Percentage change of transmission capability under different attack modes

从图3可以看出，在随机攻击模式下，系统输电能力百分比变化最小，最高度数节点攻击模式次之，输电能力百分比变化最大的两种攻击模式分别是最高脆弱性贡献节点攻击和综合权重排序1下的最高脆弱度节点攻击，其变化大于最高介数节点攻击模式。这说明节点脆弱性贡献指标和依据本文指标辨识出的脆弱节点是合理的。

表8列出综合权重下部分节点的模糊综合评价结果，按最大隶属度原则，表中所列5个节点分属5个不同的脆弱等级。节点16的第5级备择集元素的隶属度为0.424 1，与其他脆弱等级隶属度相比最大，属极高脆弱等级。节点38的第1级备择集元素的隶属度为0.466 3，与其他脆弱等级隶属度相比最大，属极低脆弱等级。同时注意到，节点16的极低脆弱等级的隶属度为0，节点38的极高脆弱等级隶属度为 0。当节点脆弱性指标与事故实际严重程度并不存在简单关系，不能对节点脆弱性进行严格排序时，模糊综合评价结果仍然可以挑选出极高脆弱等级节点，过滤掉极低脆弱等级节点，为节点脆弱性排序提供参考意见。

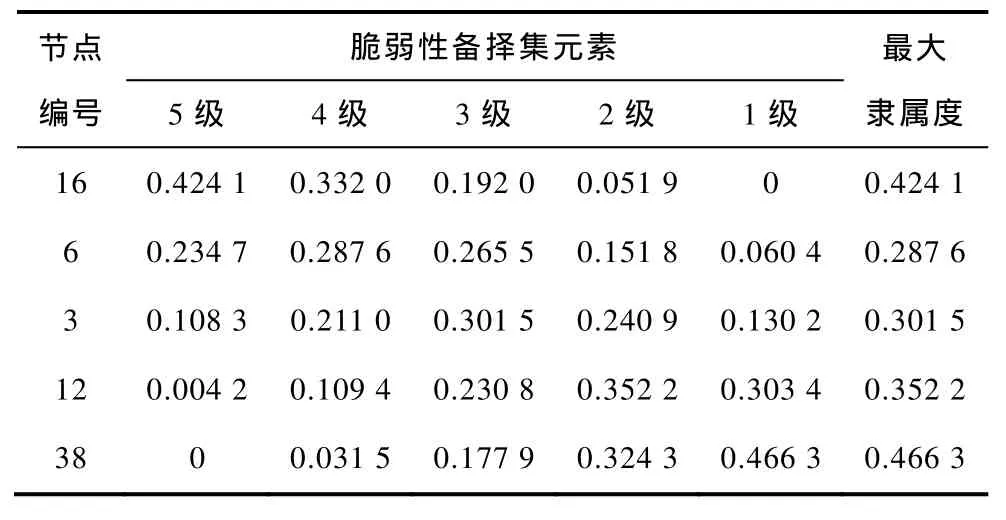
表8 综合权重下的模糊综合评价结果Tab.8 Results of fuzzy comprehensive evaluation under integrated weight

表9列出不同权重下采用最大隶属度原则对节点脆弱性的分类情况，限于篇幅，仅列出不同脆弱等级下的部分节点。结合表7可以看出，脆弱等级较高的节点都包含在采用相应权重体系的最优评价法和综合得分法中，体现三种方法在相同权重体系下的一致性。脆弱等级为极高和极低的节点在不同权重下基本保持一致，且有效性系数比其他脆弱等级节点高，在一定程度上说明本文方法在区分严重和不严重节点方面具有较高可信度。因此，在得到系统可以滤除的不严重节点集合后，剩余节点就可以作为具有潜在风险的节点，留待详细的计算分析。此外，若想提高指标体系有效性的等级，可以选取更加合理且具区分度的指标集，指标的有效性系数越高，在一定程度上说明该指标处于该脆弱等级的可信度越高。

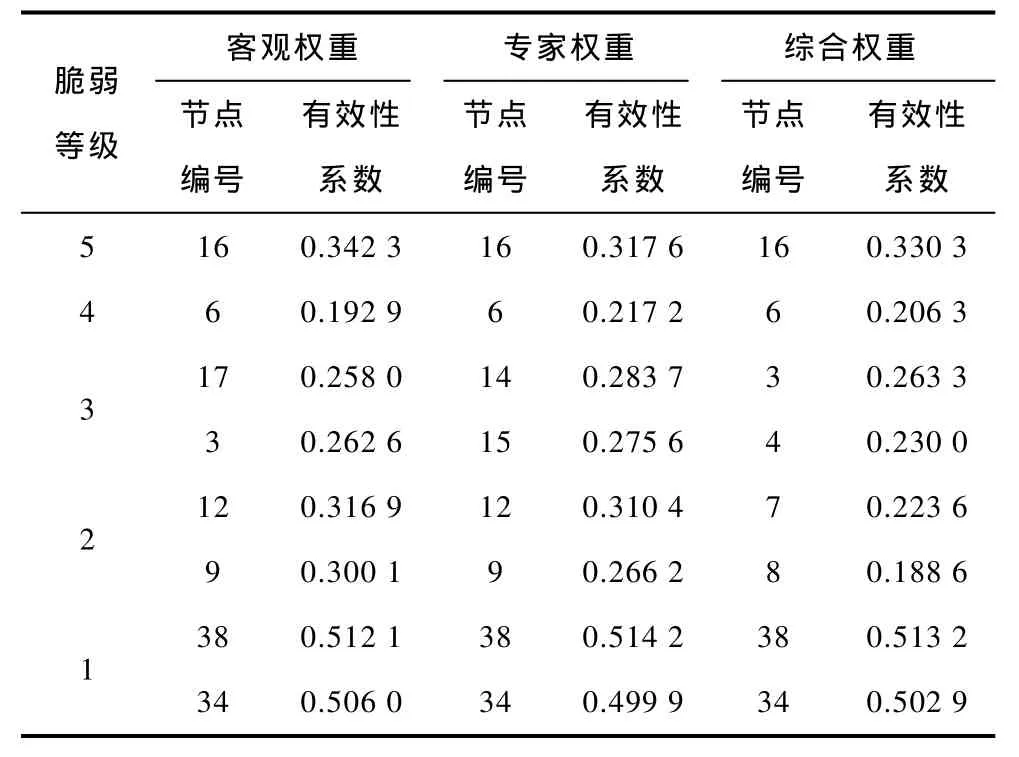
表9 不同权重下的节点脆弱性分类Tab.9 Classification of vulnerability node under different weights

6 结论

（1）效用风险熵克服了熵权计算中仅考虑指标概率不确定性的缺陷，将节点的价值系数体现在节点客观权重中。专家权重采用三标度法，克服过多标度造成应用AHP法时的困难。采用更为合理的效用风险熵权和专家权重结合方式，实现节点数据信息的客观性和专家偏好主观性的良好结合。

（2）采用最优评价法和综合得分法对系统节点进行了多方案完全排序。对于具有不同拓扑结构特征的电网，运行人员可以根据电网结构的长期统计和运行经验，选择不同的权重参与方案和排序方法。

（3）采用最大隶属度法对节点脆弱性进行分类，并通过节点隶属度有效性系数对节点脆弱性分类的可信度进行讨论。选取更加合理的节点评价指标集将有可能增加节点脆弱性分类的可信度。

（4）本文方法可扩展到支路脆弱性的评估。

[1] 王鹏. 强外力骚扰电力系统及其防护[J]. 电网技术,2006,30(2): 27-31.

Wang Peng. Power system under external force harassment and its safeguard[J]. Power System Technology,2006,30(2): 27-31.

[2] Ten C W,Liu C C,Govindarasu M. Vulnerability assessment of cybersecurity for SCADA systems[J].IEEE Transactions on Power Systems,2008,23(4):1836-1846.

[3] 贺海磊,郭剑波. 考虑共因失效的电力系统地震灾害风险评估[J]. 中国电机工程学报,2012,32(28):44-54.

He Hailei,Guo Jianbo. Seismic disaster risk evaluation for power systems considering common cause failure[J]. Proceedings of the CSEE,2012,32(28):44-54.

[4] 苏慧玲,李扬. 从电力系统复杂网络特性探讨元件的脆弱性[J]. 电力系统自动化,2012,36(23): 12-17,77.

Su Huiling,Li Yang. Electrical component vulnerability analysis from complex network characteristics of power systems[J]. Automation of Electric Power Systems,2012,36(23): 12-17,77.

[5] 赫南,李德毅,淦文燕,等. 复杂网络中重要性节点发掘综述[J]. 计算机科学,2007,34(12): 1-5,17.

He Nan,Li Deyi,Gan Wenyan,et al. Mining vital nodes in complex networks[J]. Computer Science,2007,34(12): 1-5,17.

[6] Barabási A L,Albert R. Emergence of scaling in random networks[J]. Science,1999,286(15): 509-512.

[7] Albert R,Albert I,Nakarado G L. Structural vulnerability of the North American power grid[J]. Physical Review E,2004,69(2): 1-10.

[8] 陈晓刚,孙可,曹一家. 基于复杂网络理论的大电网结构脆弱性分析[J]. 电工技术学报,2007,22(10):138-144.

Chen Xiaogang,Sun Ke,Cao Yijia. Structural vulnerability analysis of large power grid based on complex network theory[J]. Transaction of China Electrotechnical Society,2007,22(10): 138-144.

[9] 丁明,韩平平. 加权拓扑模型下的小世界电网脆弱性评估[J]. 中国电机工程学报,2008,28(10): 20-25.

Ding Ming,Han Pingping. Vulnerability assessment to small-world power grid based on weighted topological model[J]. Proceedings of the CSEE,2008,28(10):20-25.

[10] 徐林,王秀丽,王锡凡. 基于电气介数的电网连锁故障传播机理分析与积极防御[J]. 中国电机工程学报,2010,30(13): 61-68.

Xu Lin,Wang Xiuli,Wang Xifan. Cascading failure mechanism in power grid based on electric betweenness and active defence[J]. Proceedings of the CSEE,2010,30(13): 61-68.

[11] Bompard E,Masera M,Napoli R,et al. Assessment of structural vulnerability for power grids by network performance based on complex networks[J]. Computer Science,2009,55(8): 144-154.

[12] Bompard E,Napoli R,Xue F. Analysis of structural vulnerabilities in power transmission grids[J]. International Journal of Critical Infrastructure Protection,2009,2(1/2): 5-12.

[13] Bompard E,Wu D,Xue F. Structural vulnerability of power systems—A topological approach[J]. Electric Power Systems Research,2011,81(7): 1334-1340.

[14] 刘艳,顾雪平. 基于节点重要度评价的骨架网络重构[J]. 中国电机工程学报,2007,27(10): 20-27.

Liu Yan,Gu Xueping. Node importance assessment based skeleton-network reconfiguration[J]. Proceedings of the CSEE,2007,27(10): 20-27.

[15] Liu Yan,Gu Xueping. Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization[J].IEEE Transactions on Power Systems,2007,22(3):1267-1274.

[16] 谢琼瑶,邓长虹,赵红生,等. 基于有权网络模型的电力网节点重要度评估[J]. 电力系统自动化,2009,33(4): 21-24.

Xie Qiongyao,Deng Changhong,Zhao Hongsheng,et al. Evaluation method for node importance of power grid based on the weighted network model[J]. Automation of Electric Power Systems,2009,33(4): 21-24.

[17] 王韶,董光德,晏健. 基于最优负荷削减的小世界电网连锁故障模拟[J]. 电网技术,2012,36(6):152-156.

Wang Shao,Dong Guangde,Yan Jian. Optimal loadshedding based simulation of cascading failure in small-world power grid[J]. Power System Technology,2012,36(6): 152-156.

[18] 刘俊华,罗隆福,张志文,等. 一种考虑排序稳定分析的电能质量综合评估新方法[J]. 中国电机工程学报,2013,33(1): 70-76.

Liu Junhua,Luo Longfu,Zhang Zhiwen,et al. A new method for power quality comprehensive evaluation considering the analysis of sequence stability[J].Proceedings of the CSEE,2013,33(1): 70-76.

[19] 姜丹,钱玉美. 效用风险熵[J]. 中国科学技术大学学报,1994,24(4): 461-469.

Jiang Dan,Qian Yumei. Effect risk entropy[J]. Journal of University of Science and Technology of China,1994,24(4): 461-469.

[20] 吴文可,文福栓,薛禹胜,等. 基于马尔可夫链的电力系统连锁故障预测[J]. 电力系统自动化,2013,37(5): 29-39.

Wu Wenke,Wen Fushuan,Xue Yusheng,et al. A Markov chain based model for forecasting power system cascading failures[J]. Automation of Electric Power Systems,2013,37(5): 29-39.

[21] 龚辉,吕林,刘友波,等. 输电网脆弱线路识别的静态综合指标法[J]. 电力系统保护与控制,2013,41(11): 25-31.

Gong Hui,Lü Lin,Liu Youbo,et al. Static comprehensive index method of vulnerable lines identification of power transmission grids[J]. Power System Protection and Control,2013,41(11): 25-31.