基于区间估计的风电出力多场景下静态电压安全域研究

刘文颖 徐 鹏 赵子兰 刘福潮 许园园

（1. 华北电力大学电气与电子工程学院 北京 102206 2. 国网冀北电力有限公司信息通信分公司 北京 100053 3. 甘肃省电力公司电力科学研究院 兰州 730050 4. 国网技术学院 济南 250002）

1 引言

目前研究静态电压稳定性[1]的主要成果是基于潮流方程的最大传输功率法、灵敏度分析和潮流多解性分析等[2]，这些分析方法被称为逐点法。连续性控制变量使得运行点成为一个区域，逐点法只能对它进行近似的分析，故不能完整、系统地确定系统的安全性。域的方法通过简单的显式数学关系，来描述系统安全运行点的集合或连续的区域，这样就能对具有已知不确定性的运行点进行更系统地安全性评估。电压稳定域可根据不同的电压稳定问题分为静态电压稳定域（SVSR）、小扰动电压稳定域（SSSR）和暂态电压稳定域（TVSR）。SVSR是由满足静态电压稳定的系统运行点构成的区域。文献[3]首次使用以节点电压幅值和支路角为状态变量的线性化潮流模型和仿射变换的性质，对有功静态安全域的几何性质进行了分析描述；文献[4,5]基于电力系统注入功率空间研究建立了用于分析动态稳定和静态电压稳定的安全域分析法；文献[6]提出了基于割集功率空间的安全域，用于分析系统静态电压稳定，割集是由一些调度员较为关心的系统断面组成，割集功率空间上超平面形式的稳定域具有维数低、便于计算的优点。

随着风电技术的日渐成熟，风电并网容量不断增加，在含风电的电网规划运行中，除了负荷预测误差、发电机非计划启停等不确定性因素外，高渗透率下的风电随机性、不可控多出力场景对电网静态电压安全的影响也不容忽视[7]。然而目前国内考虑风电场出力随机性的电网静态电压安全分析方法的研究还较少。

本文以风速的 Weibull模型为基础，利用极大似然估计和Fisher信息矩阵，对已投运风电场的实测风速总体进行满足一定置信水平的区间估计，据此计算风电出力水平，来构建风电出力场景，继而借鉴文献[6]提出的基于割集功率空间的静态电压稳定域实用边界，来研究含风电场电网的静态电压稳定问题。该方法能够在风速参数未知的情况下，从发生概率角度考虑风电出力随机性对电网静态电压稳定性的影响，风电出力水平的区间估计所用数据取自实测风速，更加符合实际生产运行的工况。

2 风电出力场景的区间估计方法

场景法是基于情景分析法产生的，风电出力场景分析法则用于描述随机间歇性风电出力在未来可能发生的不确定情况，且根据不同的需要可有多种场景定义方法。文献[8]在风电场长期风速分布符合Weibull概率分布的基础上，通过将风电场出力离散化来建立风电出力多场景，并引入“适应度”来表征出力场景的实际发生比例，据此反映分区结果抵御风电场扰动并保持电压稳定的能力，文献[9]通过分析风电场群年持续出力曲线Pdur(t)与不同风电接纳能力来定义风电出力的不同场景；文献[10]将一个风电波动场景定义为各时段内所有风电机组出力值的总和，并通过风电出力状态场景矩阵W(s)予以表征。其中，以概率方法为基础的风电出力多场景定义方法能很好地体现未来场景的重要程度（出现概率），并在电力规划领域中得到了广泛关注与成功应用[11,12]。

但上述关于出力场景的方法均是在风速的数学期望和方差已知的情况下构建的，而实际风速的随机性特征显著，且计算期望和方差需要的尺度参数、形状参数亦随时空分布不同而有所变化，这种差异性随风电场/集群范围的增大而愈加明显。因此由上述方法得到风电出力多场景较实际出力水平存在一定误差。

为解决传统方法存在的以上不足之处，本文利用实测风速对实际风速总体进行参数区间估计，求解出满足一定置信水平的风速期望区间。

区间估计与点估计一样，均是参数估计的一种形式，都可在总体参数未知的情况下通过实测样本计算出参数估计值。就描述风电随机波动性而言，区间估计更为适合，它通过从总体中抽取的样本，根据一定的正确度与精确度的要求，构造出适当的区间，以作为总体的分布参数的真值所在范围的估计，该区间能以较大概率包含实际的风电出力波动范围；就估计过程而言，区间估计与点估计之间又存在一定的互补性，特别是在具有多元复杂参数的分布函数中，点估计能为区间估计的中间过程提供必要的参数估计值以完成全体参数的区间估计。本文在进行区间估计时，恰好是利用了点估计的极大似然估计来求解出二元分布函数的区间估计。

以常用的三参数Weibull分布作为风速模型

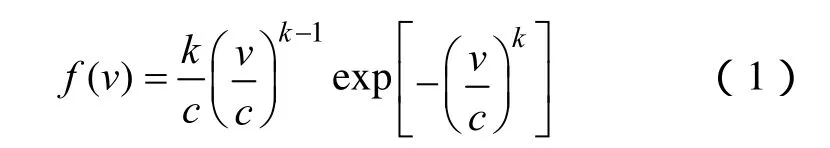
式中，k、c均为Weibull分布参数，其中k为形状参数，c为尺度参数。

虽然风力发电机有多种类型，但其出力和风速的关系基本相似[13,14]，如图1b功率输出曲线所示。图中，Pr为风力发电机额定输出功率，vi为切入风速，vr为额定风速，vo为风机切出风速。

由 Weibull分布密度函数可求得其随机变量X的n阶矩阵为

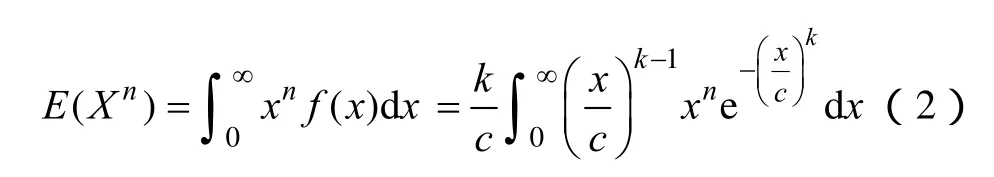
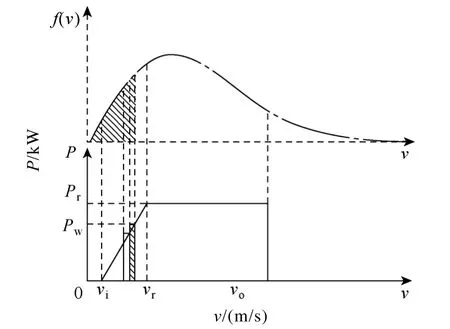
图1 风力发电机功率-风速曲线Fig.1 Wind power-wind speed curse

设

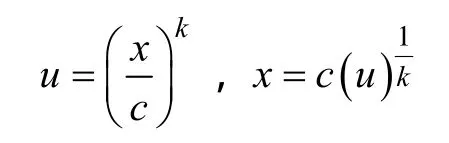
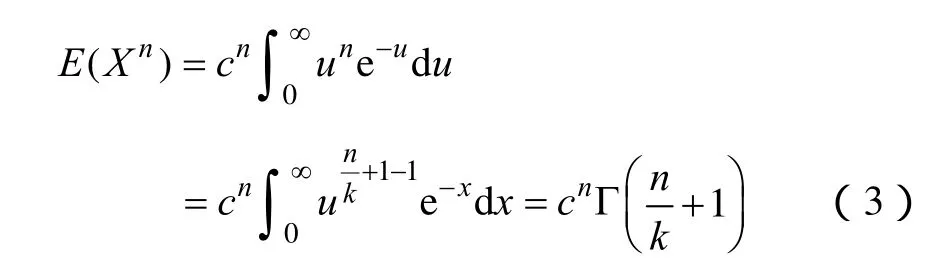
因此可用Gamma函数

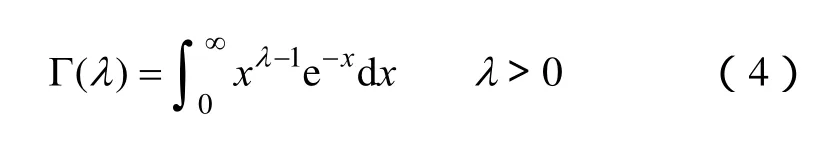
求取Weibull分布的数学期望和方差

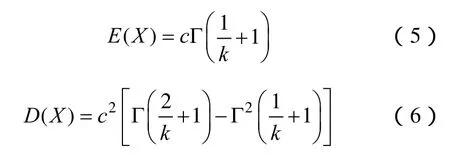
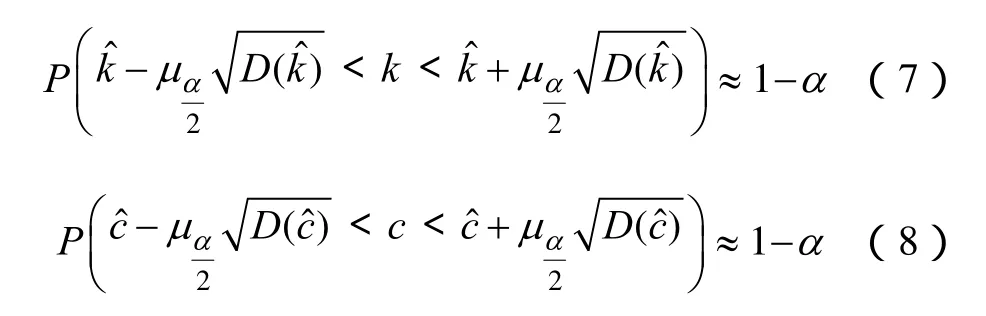
通过对风电场的风速进行取样，生成的风速样本 ｛vi｝ （i=1,2,…,n）是来自于总体T～W(k，c)，将样本 ｛vi｝ （i=1,2,…,n）代 入 式 （1），取 对 数 并 求 和可得到似然函数

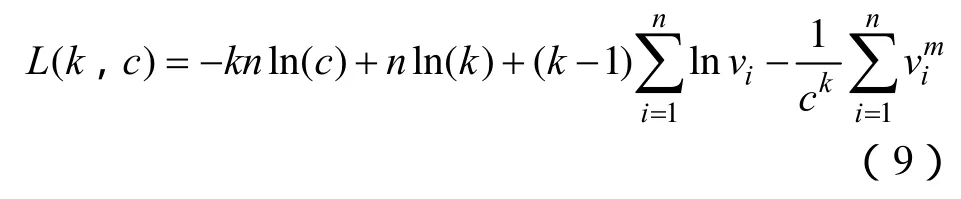
对 (,)Lkc求偏导数得关于k、c的表达式

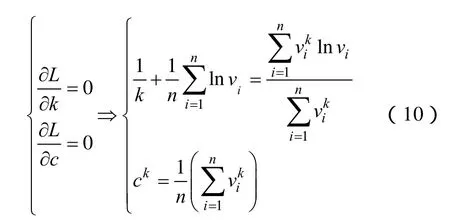
化简式（10）的第一个等式，可得形状参数k的极大似然估计计算表达式

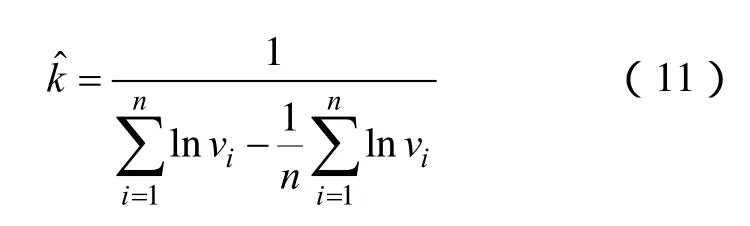
将式（11）代入式（10）的第二个等式，则可求得尺度参数的极大似然估计值。参数k、c的方差和协方差是Fisher信息矩阵的逆矩阵[16]为

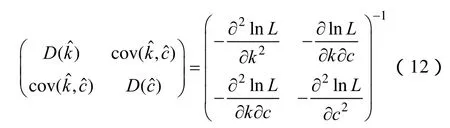
在置信水平α给定的情况下，根据式（7）、式（8）求得参数k、c的区间估计；再由式（5）可得风速期望估计区间。需要说明：①为得到较可靠的置信区 间，样本 ｛vi｝ （i=1,2,…,n）应尽可 能 大；②当风速抽样误差偏大时，需采用较高的置信水平，此时得到的置信区间较宽；当风速抽样误差偏小时，可采用较低的置信水平，此时得到的置信区间较窄。

3 基于风电出力场景的静态电压安全域

根据世界各国实际的风电场运行经验，并网风电的随机性波动使得无功功率在网源间相互转移，静态电压失稳问题时有发生[17]。而如上节所述，风电的随机性有一定的概率分布可寻，利用实测风速样本估计出的风电场出力水平，即风电出力场景具有较大的实际发生概率，出力区间外的运行点由于发生次数较少，可忽略其对静态电压稳定的影响。

“域”的方法是在概率安全构想基础上提出的一种较新的电力系统安全稳定研究新方法，尤其在因风电随机性引起的运行点具有已知不确定性时，也能系统地估计其安全性或安全概率[18]。

基于潮流的系统静态安全域被定义为满足系统潮流方程，且不发生系统安全约束越限的所有运行点的集合。其中静态安全约束条件主要包括以下 3方面。

（1）电压约束

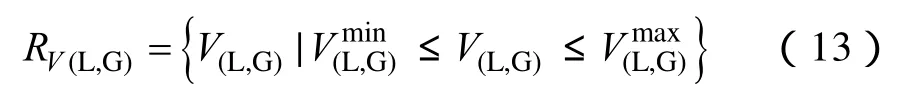
式中，(L,G)V表示发电机节点或负荷节点的电压；分别表示电压上、下限。

（2）线路潮流约束

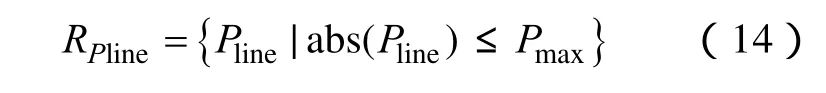
式中，Pline为线路有功功率；Pmax为功率上限。

（3）发电机出力约束

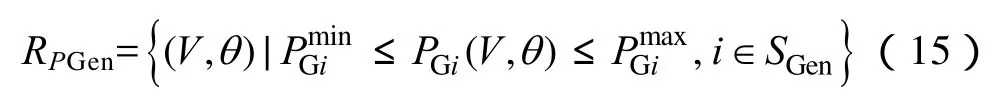
由IEEE关于电压稳定的定义可知，PV曲线上NP点可作为系统静态电压稳定的临界点，临界点以内的系统运行点所组成的区域即为系统静态电压稳定域。临界点一般是在一定的负荷增长方式下，采用连续潮流法，逐渐增负荷直至使运行点落在系统PV曲线的NP点处来获得，在高风电渗透率下，风力发电机发出或吸收的无功会随风速变化而出现大幅波动，系统电压临界点的位置不仅取决于负荷的增长方式及其大小，不可控风电出力引起的无功功率转移也将极大地影响 NP点的落点。图 2和图3给出了在IEEE 10机39节点系统中，改变G8注入有功功率水平前后节点BUS04、BUS05、BUS06、BUS07、BUS08、BUS09的电压 PV曲线的对比情况。

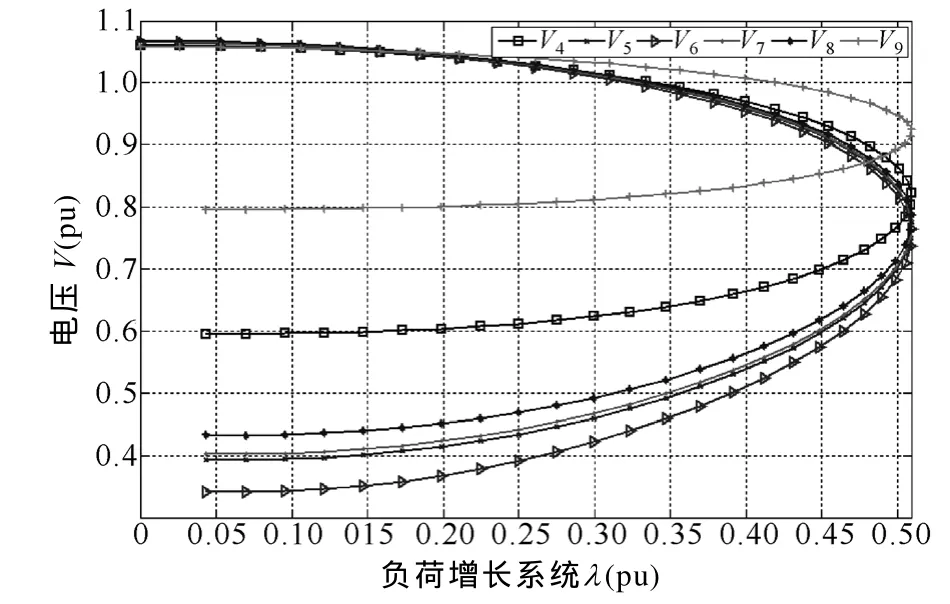
图2 G8注入功率为500MW时节点PV曲线Fig.2 Nodes PV curse when G8 power penetration equals 500MW

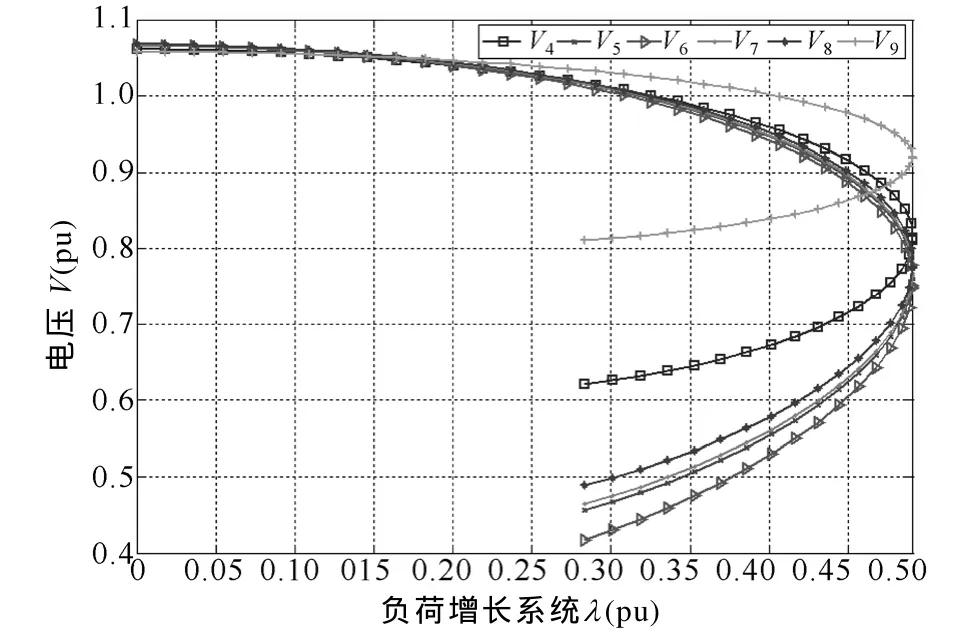
图3 G8注入功率为600MW时节点PV曲线Fig.3 Nodes PV curse when G8 power penetration equals 600MW

从图2和图3的分析中可看出，当G8注入功率由 500MW增加至600MW时，系统运行点的稳定区间明显减小，由此可看出，风电注入功率的区间变化必然引起静态电压稳定域边界的改变。

前述利用极大似然估计和Fisher信息矩阵求得的风电出力场景，其实质是满足一定置信水平 1-α的风电出力区间。且由概率论的参数区间估计知识可知，在相同的样本容量情况下，置信水平越高，置信区间越宽，也即风电出力场景下的出力范围越大，由风电出力场景上限和下限确定的节点静态电压安全稳定裕度差别也较明显，而这种明显的差别对系统静态电压稳定的影响可从图2、图3中的PV曲线对比看出。为保证所得到的静态电压稳定域边界能准确描述运行点的安全状态，本文取风电出力场景上、下限确定的域边界的交集作为该场景下最终的安全域边界。

节点电压失稳主要是因为节点所承受功率变化的能力不强，无功支撑不足，一般将这些节点称为弱节点。风电随机间歇性以及对无功功率的需求更容易使系统出现电压失稳。而同一网络拓扑结构下的节点间存在一定的电气关联，使得弱节点和非弱节点的分布具有局部性特征，这样就为应用割集的概念提供了便利。

割集是指能将系统分割为两部分的一组线路集合，割集功率空间则是指以系统割集线路上的潮流为坐标所构成的空间。适当选择能将弱节点集和非弱节点集分开的系统割集，并监视该割集上每条线路的有功潮流和无功潮流，能很好地反映系统电压稳定的特征，并且与注入功率空间相比，基于割集功率空间的静态电压安全域具有维度低、易于计算的特点，运行人员可选择自己较为关注的割集线路作为分析影响系统静态电压稳定的依据。

本文借鉴文献[6]提出的基于临界割集功率空间上的电力系统静态电压稳定域边界表达式见（16），计算得到风电多场景下的电网静态电压稳定域实用边界。

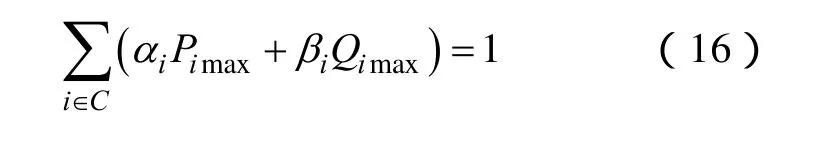
式中，C表示临界割集；Pimax、Qimax分别表示C中线路i的有功、无功潮流极限；αi、βi分别表示与割集线路潮流相关的超平面系数，一般经仿真计算并结合最小二乘法拟合得出。而系统临界割集的获得则是先通过模态分析[19]法获得系统在发生电压失稳时的弱节点集，再根据运行人员的关注程度来确定临界割集中的各条线路，在此不再赘述。

4 基于风电出力场景的静态电压安全域计算步骤

（1）测量生成实际风速样本 ｛vi｝ （i=1,2,…,n）；

（2）根据式（10）求得总体 Weibull分布中的形状参数k、尺度参数c的极大似然估计值、，再根据式（12）的Fisher信息矩阵求得D()、D()。

（3）根据式（7）、式（8）求得满足置信度α的参数k、c的置信区间。

（5）在风电平均出力场景下，分别以出力估计区间的上、下限值为注入功率，利用连续潮流法求得系统临界割集。

（6）最后利用式（16）求得风电平均出力场景下的系统静态电压安全域实用边界。

5 实例验证

IEEE 39节点系统接线方式如图4所示，其中包括10台发电机，34条线路。

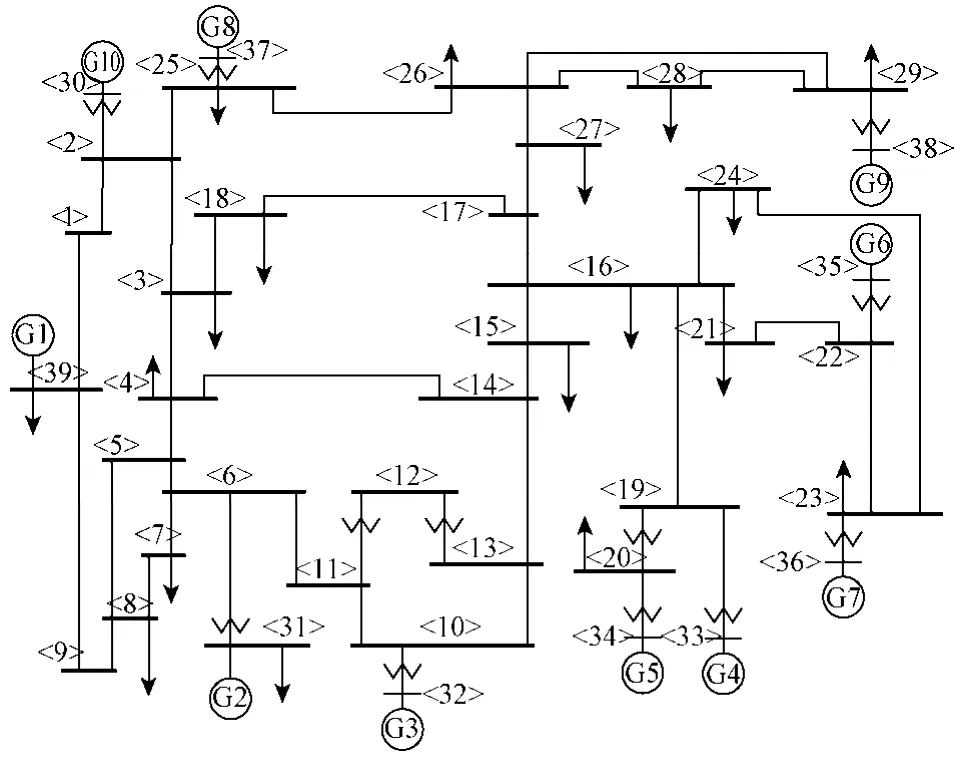
图4 IEEE 39节点系统Fig.4 IEEE 30 bus system

将 G8设置为以感应式风力发电机为主的风电场等值发电机，风电场单台额定容量为2MW，设共300台风电机组。发出有功时对应吸收的无功功率取发电机容量的 20%～25%[15]。利用 Matlab中的Weibull随机数发生器，产生风速样本（样本大小为200）如图5所示。

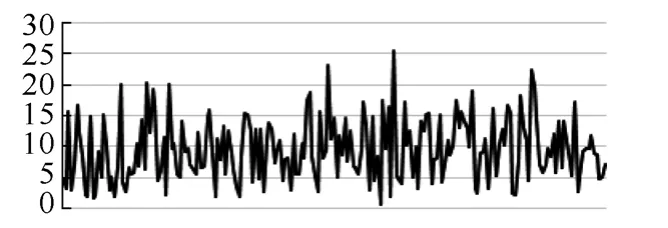
图5 随机风速样本Fig.5 Wind speed samples

根据式（10）求出该样本所在总体的形状参数、尺度参数的极大似然估计值分别为

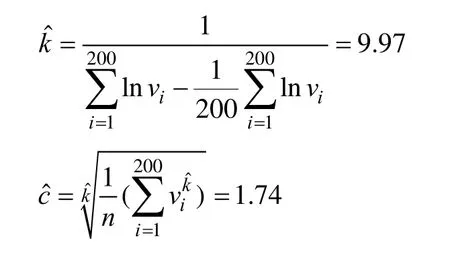
再由式（7）、式（8）和式（11）可求得置信区间。

考虑风速样本由指定风速参数的函数发生器生成，抽样误差相对较小，因此置信水平宜取常用参考值中较小的量，本文取0.1α=时，=1.552 8，=0.474 1。因此，可得在满足置信水平为0.9的前提下，k、c的估计区间为

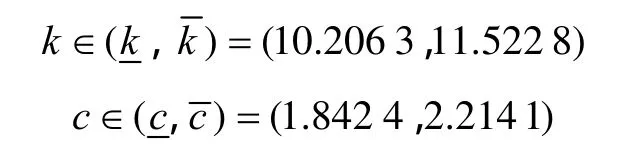
由式（5）得出风速区间为v∈( 9.0392，10 . 2051)，据此计算风电平均出力场景下单台风力发电机的发出有功功率为1.21～1.87MW。

根据图1所示风速与P的关系，在风电平均出力场景下，采用连续潮流法求得系统弱节点集及对应的临界割集见表1。

表1 系统弱节点集与临界割集Tab.1 Weak points set and critical cut-set of system

可以看出，在不同的风电出力场景下，弱节点集合所包含的节点不尽相同，且对应不同的系统临界割集。根据表1所示临界割集信息，采用文献[6]提出的静态电压安全域实用边界拟合方法，对不同场景下的临界割集边界表达式进行拟合，所得结果见表2。

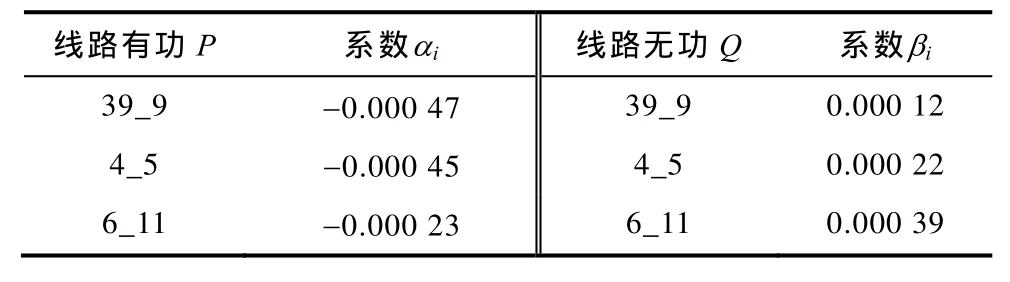
表2 系统临界割集Tab.2 Critical cut-set of system

由于临界割集线路数为3条，且考虑到在实际运行中无功功率的就地平衡，得到的基于割集功率空间的静态电压安全域处在三维割集有功功率空间内，通过Matlab编程计算并绘制静态电压安全域如图 6所示。图中虚线部分是在已知风速的数学期望和方差情况下得到的静态电压安全域边界，深色部分是基于区间估计的风力场景下得到的静态电压安全域。

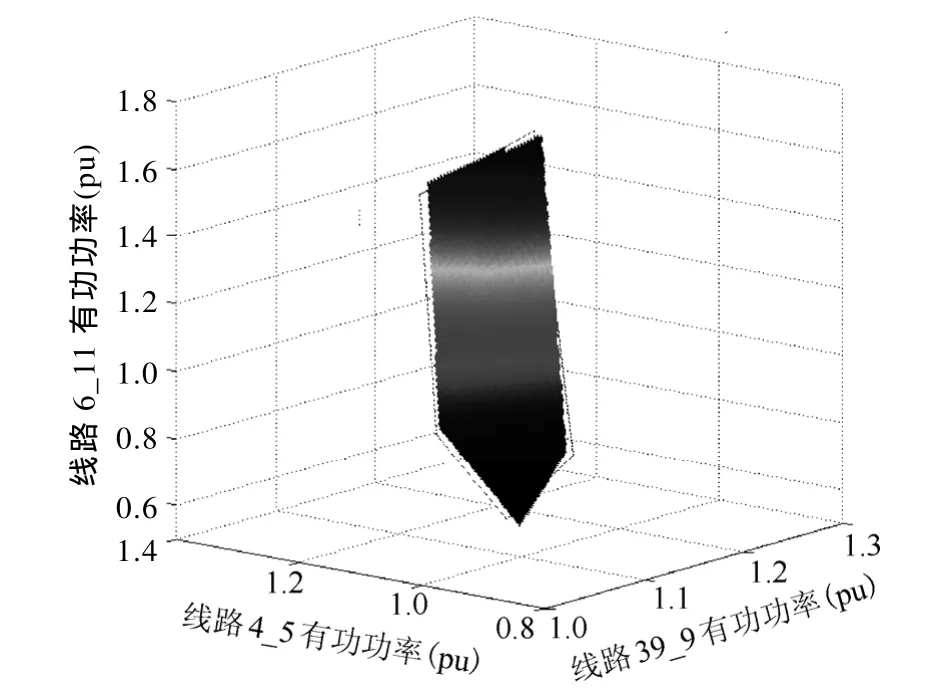
图6 静态电压安全域Fig.6 Static voltage stability region

从图4可看出，通过参数估计得到的静态电压安全域与参数已知时的域边界几近相同，经验证其误差满足实际应用的需求。需要说明的是，基于参数估计的静态电压安全域，取自以风电出力估计区间上、下限值各自确定的安全域的公共部分。

6 结论

本文从风速的 Weibull分布特性出发，在风速的期望和方差未知的情况下，以实测风速数据为基础，通过参数估计来求得风电出力场景，并据此来求解基于割集功率空间上的静态电压安全域。该出力场景由于满足较大的发生概率，能在一定程度上适应风电随机性变化，减小了风电恒定出力水平下求得的静态电压安全域与实际域边界的误差。对于基于参数估计求得的风电出力场景与参数已知时求得的风电出力水平之间的差别，在实例部分中图 4表征的域边界可看出，其误差较小，可以满足实际应用的要求。

[1] 余贻鑫,陈礼义. 电力系统的安全性与稳定性[M].北京: 科学出版社,1988.

[2] 王承民,蒋传文. 基于支路电流状态变量的灵敏度分析方法研究[J]. 电工技术学报,2006,21(1): 42-46.

Wang Chengmin,Jiang Chuanwen. Research on sensitivity analysis method based on line current variable[J].Transactions of China Electrotechnical Society,2006,21(1): 42-46.

[3] 余贻鑫,冯飞. 电力系统有功静态安全域[J]. 中国科学(A辑),1990,6: 664-672.

[4] 冯飞,余贻鑫. 电力系统功率注入空间的动态安全域[J]. 中国电机工程学报,1993,13(3): 14-22.

[5] 韩琪. 电力系统注入功率空间的静态电压稳定域[D]. 天津: 天津大学,2004.

[6] 李慧玲,余贻鑫,韩琪,等. 割集功率空间上静态电压稳定域的实用边界[J]. 电力系统自动化,2005,29(4): 18-23.

Li Huiling,Yu Yixin,Han Qi,et al. Practical boundary of static voltage stability region in cut-set power space of power systems[J]. Automation of Electric Power Systems,2005,29(4): 18-23.

[7] 朱星阳,刘文霞,张建华,等. 电力系统随机潮流及其安全评估应用研究综述[J]. 电工技术学报,2013,28(10): 257-270.

Zhu Xingyang,Liu Wenxia,Zhang Jianhua,et al.Reviews on power system stochastic load flow and its applications in safety evaluation[J]. Transactions of China Electrotechnical Society,2013,28(10): 257-270.

[8] 乔梁. 含风电场的电力系统电压控制分区方法研究[D]. 重庆: 重庆大学,2010.

[9] 崔场. 大规模风电场群联网的源网协调性研究[D].北京: 华北电力大学,2011.

[10] 袁越,吴博文,李振杰,等. 基于多场景概率的含大型风电场的输电网柔性规划[J]. 电力系统自动化设备,2009,29(10): 8-12.

Yuan Yue,Wu Bowen,Li Zhenjie,et al. Flexible planning of transmission system with large wind farm based on multi-scenario probability[J]. Electric Power Automation Equipment,2009,29(10): 8-12.

[11] 杨高峰,康重庆,谷兴凯,等. 电力市场中基于情景分析的电网规划方案适应性评估[J]. 电网技术,2006,30(14): 64-70.

Yang Gaofeng,Kang Chongqing,Gu Xingkai,et al.Scenario analysis based flexibility evaluation of power grid planning under deregulation[J]. Power System Technology,2006,30(14): 64-70.

[12] 郑智,周双喜,徐飞,等. 基于多场景和模糊技术的综合无功规划[J]. 电力系统自动化,2007,31(4):41-45.

Zheng Zhi,Zhou Shuangxi,Xu Fei,et al. Comprehensive reactive power planning based on multiscenario and fuzzy technique[J]. Automation of Electric Power Systems,2007,31(4): 41-45.

[13] 赵振宙,郑源,高玉琴,等. 风力机原理与应用[M].北京: 中国水利水电出版社,2011.

[14] 洪芦诚,石立宝,姚良忠,等. 计及风电场发电功率不确定性的电力系统模糊潮流[J]. 电工技术学报,2010,25(8): 116-130.

Hong Lucheng,Shi Libao,Yao Liangzhong,et al.Fuzzy modelling and solution of load flow incorporating uncertainties of wind farm generation[J]. Transactions of China Electrotechnical Society,2010,25(8):116-130.

[15] 茆诗松,王静龙,濮晓龙. 高等数理统计[M]. 北京:高等教育出版社,1998.

[16] 王兆军,邹长亮. 数理统计讲义[D]. 天津: 南开大学,2011.

[17] 朱星阳,张建华,刘文霞,等. 风电并网引起电网电压波动的评价方法及应用[J]. 电工技术学报,2013,28(5): 88-98.

Zhu Xingyang,Zhang Jianhua,Liu Wenxia,et al.Evaluation methodology and its application of voltage fluctuation in power network caused by inter-connected wind power[J]. Transactions of China Electrotechnical Society,2013,28(5): 88-98.

[18] Liu C C. A new method for the construction of maximal steady-state security regions of power systems[J]. IEEE Transactions on Power & Systems,1986(4): 19-27.

[19] Gao B,Kundur P. Voltage stability evaluation using modal analysis[J]. IEEE Transactions on Power Systems,1992,7(4): 1529-1542.