华北地区大地电性结构三维建模及磁暴感应地电场有限元计算

王泽忠 董 博 刘春明 刘丽平 刘连光

（1. 华北电力大学高电压与电磁兼容北京市重点实验室 北京 102206 2. 华北电力大学电气与电子工程学院 北京 102206 3. 中国电力科学研究院 北京 100192）

1 引言

太阳风暴携带的带电粒子会导致地球磁场发生全球性剧烈变化，并在具有导电性的地质结构中感应出地电流。地电流在大地导体中流通会使地面不同位置出现电位差。在地面电位差的作用下，地磁感应电流（GIC）通过交流电网的中性点、油气管网的管道壁及高铁系统的铁轨等接地点与大地构成流通回路[1]，引起变压器直流偏磁、管道外壁腐蚀、破坏阴极保护系统和铁路信号故障等一系列安全问题。而地面电位差是由地电场引起，因此准确求解地电场对于磁暴侵害技术系统的防护和治理至关重要[2]。

确定地电场的分布不仅要了解地磁场的时变情况，还要考虑大地电性结构的实际分布[2,3]。我国所处的中低纬地区地磁场变化频率一般位于 0.01～0.000 1Hz之间[4,5]。若大地电导率只随深度分层变化，可用地面波阻抗表征电性结构，与地磁场相乘求得地电场。这种方法称作平面波法[6]。倘若输电线路、油气管网或铁路网沿海岸线架设，或途经内陆不同地质结构交界面、大地断层等电导率突变显著的地区，则需要考虑海水与陆地之间、不同地质结构之间电导率的横向变化。进一步地，对于我国特高压长距离输电线路，其空间尺度达到几百公里乃至上千公里[7,8]，所覆盖的区域包含多种地质构造，大地电导率是空间三维分布的。文献[9,10]建立了包含海陆分界面的二维大地电导率模型，但没有采用电导率的实测数据；文献[11-13]是将北美、欧洲的大范围区域分解成多个独立的一维结构，在每个一维结构内用平面波法求得地电场，再叠加起来获得全区域的地电场分布。这种方法没有考虑电导率的横向差异对地电场的影响。

本文采用我国大地电磁测深数据构建华北地区大范围三维电导率模型。以磁暴时地磁台测得的地磁场变化数据作为边界条件，应用有限元法求解三维感应地电场，给出了不同电导率结构影响地电流分布的规律。应用地面电场的计算结果，考察了规划中的“三华”特高压同步电网“东纵”和“北横”部分线路中选定变电站间的电位差分布情况，为进一步制定特高压电网防范磁暴侵害的技术方案、优化电网设计及台站选址提供依据。

2 基本方程与建模方法

2.1 基本方程

由于地磁场变化的频率很低，与传导电流相比，位移电流可以忽略。研究感应地电场时假定大地导体为各向同性结构，磁导率为μ0。采用A-φ位表示的伽辽金加权余量方程为[14]

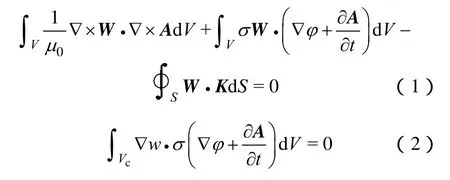
式中，V为整个求解域；S为场域边界；Vc为导体区；标量权函数w等于基函数，矢量权函数W代表w与直角坐标系的单位矢量ex、ey和ez相乘得到的3个矢量权函数[15]；K定义为

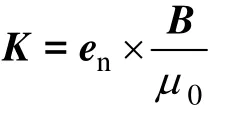
其中，en为边界面的外法向。则K的大小等于边界处磁场强度Bμ0的切向分量。假设各单元上的形状函数为N（ii=1,2,…,np，i为np单元中的节点总数），则A和φ在各单元上的插值函数为

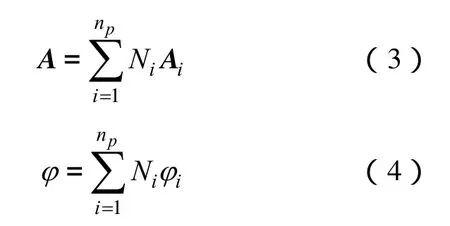
将形状函数在全部单元上叠加得到基函数序列，与节点上的A和φ组成近似函数，代入式（1）和式（2），离散成代数方程组，求解全部节点上的A和φ，进一步可求得磁感应强度、电场强度和电流密度。

2.2 建模方法

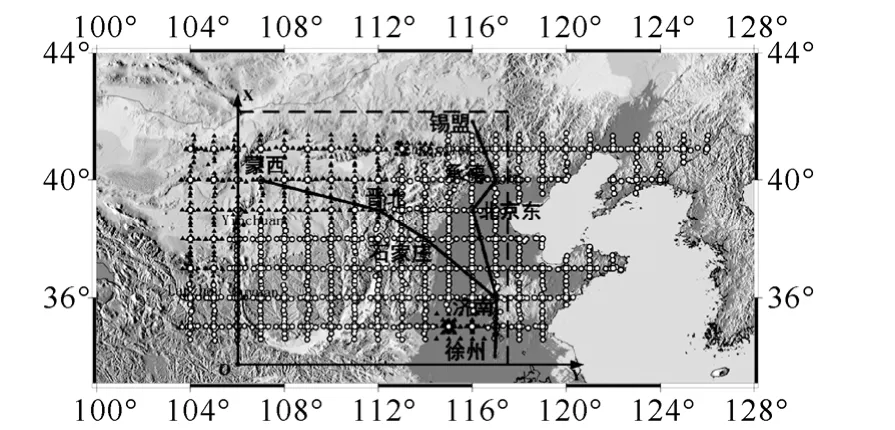
图1 华北地区三维电导率模型范围与“三华”特高压电网部分规划线路示意图Fig.1 Sketch of three-dimensional conductivity structure of North China and two selected UHV transmission lines

根据大地电磁测深法观测和解释的华北地区地质构造成果[16-19]，不考虑岩石磁性和地面系统中导磁材料的影响，建立三维电导率模型，如图1所示。图中虚线与坐标轴围成的区域为建模区域。图2给出了地面附近的电性分布图（实测数据为电阻率）。通过与我国“三华”特高压同步电网规划图对比发现，“东纵”线路的锡盟至徐州段、“北横”线路的蒙西至济南段位于模型覆盖的范围内，两条线路的走向及拟建变电站的大致选址位置也在图1中标出。

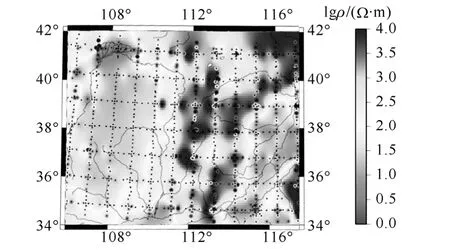
图2 模型地面附近电导率分布图（以电阻率形式给出）Fig.2 The conductivity near the Earth’s surface at North China shown as resistivity

建模时忽略地球曲率影响，选取直角坐标系，模型的南北范围为888km，东西范围约为962.5km。考虑到趋肤效应，取模型下边界为地下300km处，认为变化的电磁场在此处衰减至零。模型上边界选为地面，边界条件为模型的四周边界选取的离关心区域足够远，感应电流平行或垂直于边界面。前者对应磁场垂直边界面条件，后者对应磁场平行边界面条件。模型内部场的分布可通过式（1）与式（2）求得。

3 计算数据选取

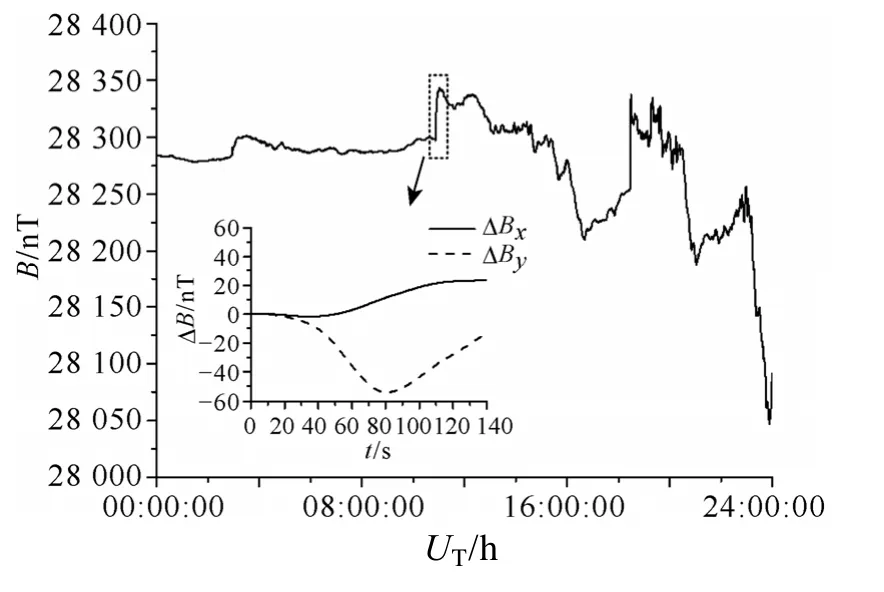
图3 2004年11月7日地磁场水平分量的记录结果Fig.3 The horizontal components of geomagnetic field observed from one observatory in Nov.7th,2004

磁暴时地磁场的变化情况可由分布于各地的地磁台站监测数据获得。本文选取2004年11月7日发生磁暴时，离建模区域最近的地磁台记录的地磁场水平分量结果，如图 3所示，数据采样间隔为 1s。用文献[20]的方法估算出，在11月7日的10：51：40～10：54：00之间的变化地磁场可能产生较大地电场。因此计算时选取这 140s的数据，相应的地磁场南北分量Bx、东西分量By相对于起始时刻的变化情况以内插图的形式绘于图中。

由于Bx和By对应的K的方向不同，四周边界条件也不同。因此在同一个模型上需要施加各自的边界条件分别计算，最后将二者结果叠加得到总的结果。

电磁场的唯一性定理表明[21,22]，场域内的场分布由区域内的基本方程和区域边界上的边界条件唯一确定。式（1）和式（2）表明，场域内的方程为涡流场方程，其中的电导率是通过实测获得的。模型的边界条件中，地面处的边界条件是实际记录的地磁场变化情况；底部边界是变化电磁场所能达到的最远边界，考虑趋肤效应后场在此处衰减为零；四周边界条件与电流和场在边界的行为吻合。计算采用的有限元法为成熟的数值方法，采用六面体八节点单元，网格剖分足够密。以上这些可以保证求解结果的可靠性[23]。

4 结果与分析

选取图1中所示的两条线路走向为电场的积分路径，选徐州站的电位为参考电位，各变电站相对于参考点的电位差分布如图4所示。曲线标号由小到大代表沿积分路径上各站距离参考站的由近到远。

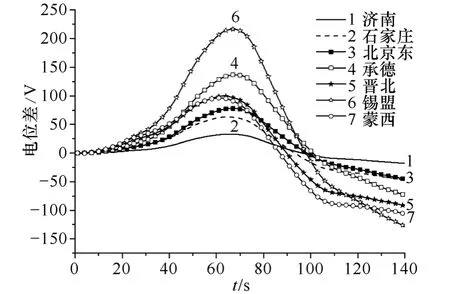
图4 两条特高压线路上各站相对于徐州站的电位差变化情况Fig.4 The voltage differences of substations at two UHV transmission lines refer to Xuzhou substation

由图4可见，电位差最大值出现在距参考点约950km的锡盟站，大小约为220V。最大值出现的时刻为第67s。而距参考点最远的蒙西站（约1 220km）并未因距离最远而出现最大电位差。造成这种现象的一个原因是由于所选时段地磁场东西分量比南北分量变化更剧烈（见图3），进而对南北走向的输电线路影响更严重。

进一步考察晋北站的电位分布情况。晋北站距参考点约770km，与蒙西站相距450km，然而对比图4中的5号和7号曲线可见，两站的电位差分布大致相同。图2显示蒙西站所处位置的大地电导率较大，而晋北站所在地区的大地电导率较小，因此大地电性结构的差异也是影响变电站电位分布的一个原因。

图 5给出了电位差达到最大时（第 67s）及其前后一些时刻地面电场的分布情况。在每个时刻图中标出了电场最大值和最小值所在的位置以及大小。

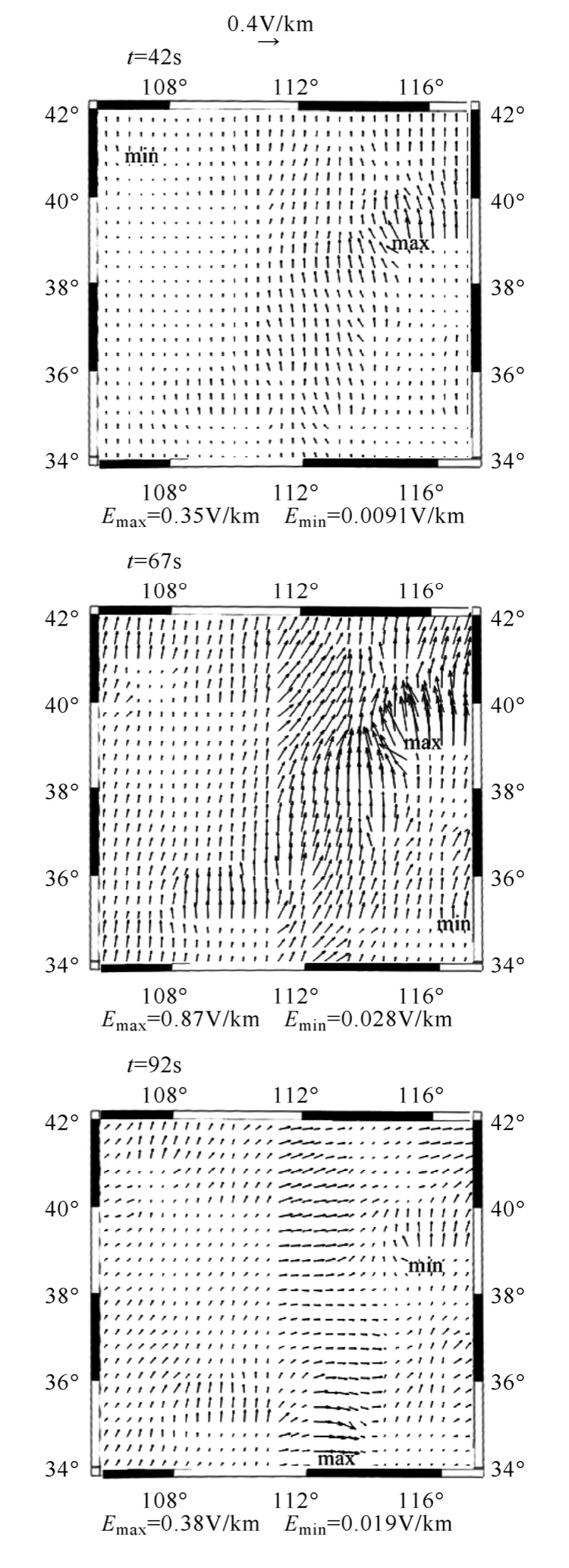
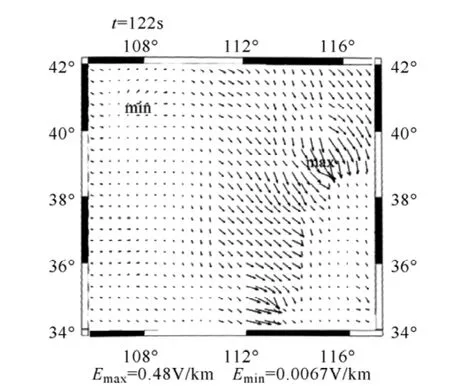
图5 电位差最大时刻及前后时刻华北地区地面电场分布情况Fig.5 The geoelectric field vectors at the moment and around the moment of maximum voltage difference

由图5可见，磁暴时的地面电场在不同时刻的大小和方向都是变化的，且同一时刻的最大值和最小值差别很大。地面电场的最大值为0.87V/km，出现在E112°、N39°附近。将各时刻最大值的位置与图2对比可见，在电导率比较小，并且周边电导率与之差异较大的地区容易产生较大的地电场。这是因为感应电流在不同电导率结构之间流通时，为了保证电流连续性，电场强度在不同电导率交界面处出现突变。而电导率的差异越大，电场强度突变程度也越大。可见电导率的横向差异会使地面电场的分布呈现空间不均匀性。

图6给出了第67s时，地下不同深度的电流密度分布情况。从图中可见，由于趋肤效应的存在，感应电流在模型上部较大，下部较小。地下200km处的最大感应电流大约是地下0.3km处最大感应电流的 1.1%。因此模型下边界选为 300km可以确保变化电磁场在此处衰减至零，从而保证计算结果的准确可靠。如果地磁场的变化频率更低，模型下边界要选取得更深一些。

5 结论

（1）首次采用三维涡流场模型分析了复杂分布的大地电性结构对磁暴时地面电场的影响。计算结果表明，电导率的不连续使得电场强度出现突变，导致地面电场呈现空间的不均匀分布，并进一步影响位于不同地质结构的变电站的电位差分布。

（2）透入深度决定了模型边界范围的选取。磁暴时地磁场的变化频率很低，电磁场会透入到地下几百公里。从防范磁暴灾害的角度出发，在这个深度范围内的大地电性构造都要加以考虑。

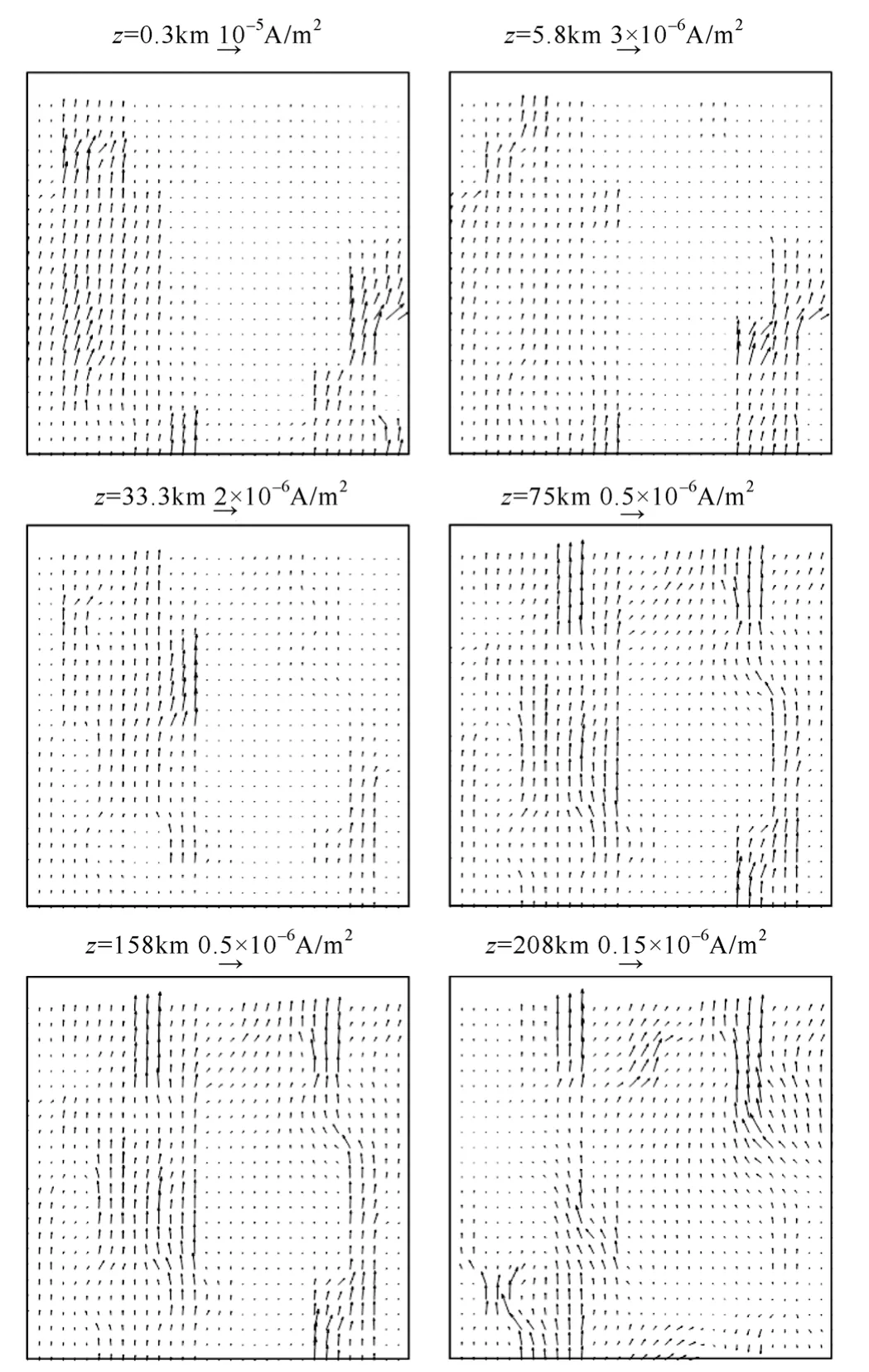
图6 电位差最大时刻不同深度处感应电流分布情况Fig.6 The induced currents at the moment of maximum voltage difference

（3）建模的电导率数据来自于大地电磁测深的探测结果，计算的地磁场数据来自于地磁台的实际记录，计算结果真实可靠，相应结论为准确评估特高压电网受磁暴侵害的影响奠定了基础，为电网规划建设及变电站选址提供了参考依据。

[1] Pirjola R. Geomagnetically induced currents during magnetic storms[J]. IEEE Transactions on Plasma Science,2000,28(6): 1867-1873.

[2] 刘连光,吴伟丽. 磁暴影响电力系统安全风险评估思路与理论框架[J]. 中国电机工程学报,2014,34(10): 1583-1591.

Liu Lianguang,Wu Weili. Security risk assessment ideas and theoretical framework for power system considering geomagnetic storm[J]. Proceedings of the CSEE,2014,34(10): 1583-1591.

[3] Zheng K,Trichtchenko L,Pirjola R,et al. Effects of geophysical parameters on GIC Illustrated by benchmark network modeling[J]. IEEE Transactions on Power Delivery,2013,28(2): 1183-1191.

[4] Kappenman J. Storm sudden commencement events and the associated geomagnetically induced current risks to ground-based systems at low-latitude and midlatitude locations[J]. Space Weather,2003,1(3):1016-1031.

[5] 刘春明. 中低纬电网地磁感应电流及其评估方法研究[D]. 北京: 华北电力大学,2009.

[6] Marti L,Rezaei Zare A,Boteler D. Calculation of induced electric field during a geomagnetic storm using recursive convolution[J]. IEEE Transactions on Power Delivery,2014,29(2): 802-807.

[7] Liu C M,Liu L G,Pirjola R. Geomagnetically induced currents in the high-voltage power grid in china[J].IEEE Transactions on Power Delivery,2009,24(4):2368-2374.

[8] Liu C M,Li Y L,Pirjola R. Observations and modeling of GIC in the Chinese large-scale highvoltage power networks[J]. Journal of Space weather and Space Climate,2014,4(A03): 1-7.

[9] Gilbert J L. Modelling the effect of the ocean-land interface on induced electric fields during geomagnetic storms[J]. Space Weather,2005,(S04A03): 1-9.

[10] Pirjola R. Practical model applicable to investigating the coast effect on the geoelectric field in connection with studies of geomagnetically induced currents[J].Advances in Applied Physics,2013,1(1): 9-28.

[11] Wei L H,Homeier N,Gannon J L. Surface electric fields for north America during historical geomagnetic storms[J]. Space Weather,2013,11(8): 451-462.

[12] Marti L,Yiu C,Rezaei Zare A,et al. Simulation of geomagnetically induced currents with piecewise layered-earth models[J]. IEEE Transactions on Power Delivery,2014,29(4): 1886-1893.

[13] Viljanen A,Pirjola R,Wik M,et al. Continental scale modelling of geomagnetically induced currents[J].Journal of Space weather and Space Climate,2012,2(A17): 1-11.

[14] 周克定. 工程电磁场数值计算理论方法及应用[M].北京: 高等教育出版社,1994.

[15] Bíró O,Preis K. On the use of magnetic vector potential in the finite element analysis of threedimensional eddy currents[J]. IEEE Transactions on Magnetics,1989,25(4): 3145-3159.

[16] 董树文,李廷栋,陈宣华,等. 我国深部探测技术与实验研究进展综述[J]. 地球物理学报,2012,55(12): 3884-3901.

Dong Shuwen,Li Tingdong,Chen Xuanhua,et al.Progress of deep exploration in mainland China: A review[J]. Chinese Journal of Geophysics,2012,55(12): 3884-3901.

[17] 董树文,李廷栋. SinoProbe—中国深部探测实验[J].地质学报,2009,83(7): 895-909.

Dong Shuwen,Li Tingdong. SinoProbe: the exploration of the deep interior beneath the Chinese continent[J]. Acta Geologica Sinica,2009,83(7): 895-909.

[18] 魏文博,叶高峰,金胜,等. 华北地区东部岩石圈到电性结构研究—减薄的华北岩石圈特点[J]. 地学前缘,2008,15(4): 204-216.

Wei wenbo,Ye Gaofeng,Jin Sheng,et al. Geoelectric structure of lithosphere beneath eastern North China:features of a thinned lithosphere from magnetotelluric soundings[J]. Earth Science Frontiers,2008,15(4):204-216.

[19] 叶高峰,魏文博,邓明,等. 青藏及华北阵列式区域大地电磁场标准观测网建设方法与实验[J]. 地质学报,2010,84(6): 801-807.

Ye Gaofeng,Wei wenbo,Deng Ming,et al. Construction methods and experiments of magnetotelluric standard network at the Tibetan plateau and north China[J]. Acta Geologica Sinica,2010,84(6): 801-807.

[20] 余华兵. 针对电网地磁感应电流的地磁场变化特征提取[D]. 北京: 华北电力大学,2014.

[21] 盛剑霓等. 工程电磁场数值分析[M]. 西安: 西安交通大学出版社,1991.

[22] 杨儒贵. 电磁定理和原理及其应用[M]. 成都: 西南交通大学出版社,2002.

[23] Dong B,Danskin D,Pirjola R,et al. Evaluating the applicability of the finite element method for modelling of geoelectric fields[J]. Annales Geophysicae,2013,31(10): 1689-1698.