Prediction of Henry's constant in polymer solutions using PCOR equation of state coupled with an activity coefficient model

Somayeh Tourani,Alireza Behvandi,*,Farhad Khorasheh

1Department of Chemical Engineering,Mahshahr Branch,Islamic Azad University,Mahshahr,Iran

2Department of Chemical and Petroleum Engineering,Sharif University of Technology,Tehran,Iran

Keywords:

A B S T R A C T

1.Introduction

Henry's constant of solutes in molten polymers is an important property because the solubility of small molecules in polymers is required in the industrial processing of most polymeric material.For example,devolatilization of low molecular weight(MW)solvents,like plasticizers,unreacted monomers,or toxic additives,is essential for safety,environmental,and product quality reasons.Development of appropriate models for prediction of Henry's constant is required for design,development,and optimization of processes involving polymer solutions.A number of thermodynamic models have been previously proposed and were successful in this regard.These models fall in two main categories including the activity coefficient models(ACMs)and equation of state(EOS)models.Some significant activity coefficient models are the classical Flory-Huggins model[1],UNIFAC-FV[2],Entropic-FV and GK-FV[3],MEFV[4],Freed-FV[5]and UNIFAC-ZM[6].Many theoretical equations of state(EOS),including the perturbed soft chain theory(PSCT)[7],GCLF[8],GC-Flory[9],COR and PCOR[10],have been used for polymer solutions.

All of these models are limited in some ways in their applicability and accuracy.In general,although the activity coefficient models appear to have better predictive capabilities to describe the behavior of complex mixtures,their use is restricted to liquid densities(characterization of the liquid phase)and low pressures,well below the critical temperature,because they are not functions of pressure.While the excess Gibbs

energy is a function of pressure,activity coefficient models do not vary with pressure.Thus,parameters regressed from data at low pressures do not correctly describe behavior at high pressures.The equations of state do not have this limitation and can be used over the entire density range and over a large range of temperatures and pressures.However,most of them are generally less accurate,and their group parameter tables are not nearly as large as those of UNIFAC,and thus restricting the types of molecular structures that can be described.However,using the normal van der Waals one- fluid mixing rules in equation of state calculations,only leads to good results for simple mixtures.Because the EOS mixing rules essentially perform the same function as activity coefficient models-describing how pure component properties relate to mixture properties-much effort has been put into developing mixing rules that can extend the capabilities of an equation of state to more complex mixtures.The excess energy family of mixing rules,specifically,has been very effective in this regard.In essence,an excess energy mixing rule is developed by equating the excess energy as calculated by an equation of state with that from an activity coefficient model.This mixing rule was useful but suffered from several limitations,including the fact that the parameters of the ACM needed different values when the model was used alone than when it was combined with an equation of state[11].Therefore,in this work we used the coupled EOS/ACM method to overcome the restrictions and improve the accuracy of equation of state models.The purpose of the present study is the application of PCOR EOS and Wilson's equation as an ACM for prediction of Henry's constant of solvents in industrially important polymer melts.For accurate description of the volumetric behavior of molten polymers,the property parameters am,bmand cmare determined by fitting the PCOR EOS with experimental specific volumes correlated by the Tait equation[12].Also it is tried to compare the temperature-dependent and temperature-independent interaction parameters of Wilson's equation by fitting them with the experimental Henry's constant data.Our objective is to obtain a simple and accurate equation that can be conveniently applied for engineering design.The rest of this paper is organized as follows: first,the PCOR EOS is presented.Subsequently,the property parameters of polymers are determined by fitting the PCOR EOS with the experimental Tait equation to describe the pressure-volume-temperature(PVT)behavior of molten polymer.Finally,Henry's constant is predicted based on PCOR EOS with the MHV1 mixing rule and Wilson's equation.

2.The Polymer Chain of Rotator(PCOR)EOS

An equation of state relates pressure,volume and temperature and is used as an effective tool for the study of the thermodynamic properties and phase behavior of pure components and mixtures.A typical equation of state requires molecular parameters for each component,and binary interaction constants for each pair of components.For a complex mixture,the estimation of such a large number of parameters can be difficult.A solution to this problem lies in the fact that although a mixture may contain a large number of different types of molecules,the number of structural groups of the molecules is relatively small.Thus by calculating the equation of state parameters in terms of group instead of molecular properties,the number of required constants is greatly reduced[13].The polymer chain of rotator(PCOR)equation of state[14,15]is a combination of the Carnahan-Starling EOS[16]for a hard sphere fluid and the Boublik-Nezbeda EOS[17]for a hard dumbbell fluid.This equation is an extension of the CORGC EOS[13,18]originally presented for small molecules,to polymers aimed at predicting the phase behavior of polymeric melts.The PCOR equation of state is as follows:

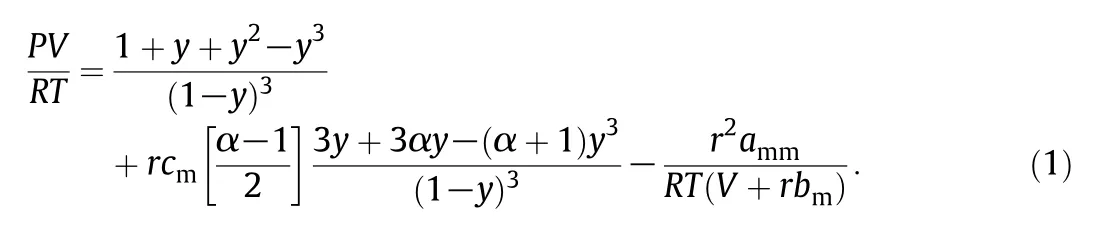
The packing factor y is equal to bm/4υ,υ =V/r is the segment molar volume and r will be equal to Mp/Mmwhere Mpis the average molar mass of polymer and Mmis the monomer molar mass.The above equation is called the molecular form of the PCOR equation of state.The PCOR equation requires three segment parameters.They are cm,effective degrees of freedom of rotation;amm,van der Waals attractive force parameter,and bm,excluded volume,equal to 4 times hard core volume.In Eq.(1),α is the rotator parameter for the single bond between two carbon atoms,which is equal to 1.078[13,14].Both bmand cmare independent of temperature,while ammin most papers is assumed to be a linear function of temperature[10].But,for better accuracy of results,it is proposed to be an exponential function of T as follow in this paper,

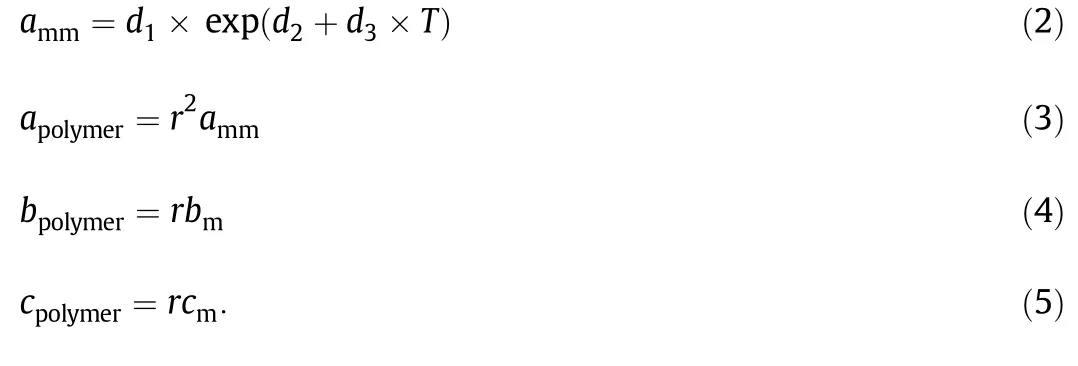
In the above equations,values of d1,d2,d3,bmand cmwere obtained by fitting the PCOR equation of state to experimental specific volumes correlated by Taitequation[12].Perhaps the most common representation of polymeric PVT data is that of Tait equation.In fact,it is not a true equation of state,but rather an isothermal compressibility model.The general form of Tait equation is:

where the coefficient C is usually taken to be a universal constant equal 0.0894.The zero-pressure isotherm V(0,T)is usually given by:

where ε is the thermal expansion coefficient.The Tait parameter B(T)is usually given by:

Thus,the Tait equation is normally a four-parameter(V0,ε,B0,and B1)representation of the experimental PVT data[12].Recently,a number of isothermal equations of state for solid and liquid polymers were introduced showing the Tait equation as an approximate solution in their formulation.Summary of PVT data for 7 homopolymers and 4 co-polymers used in this study is shown in Table 1.

Also,the Tait equation parameters for these polymers are shown in Table 2.

Table 1 Summary of PVT data for 6 homopolymers and 4 co-polymers over an extensive range of temperature and pressure

3.Extension of PCOR EOS to Polymer/Solvent Mixtures

For extension of PCOR EOS to mixtures containing both solvents and polymers,the MHV1 mixing is adopted[5]:

where zkis the mole fraction of component k,θ=amix/(bmixRT),θk=ak/(bkRT),and q1is an EOS-dependent parameter,which was set to-0.64663 as used by Holderbaum and Gmehling[19].Considering these mixing rules for a,b and c,the Henry's constantand fugacity coefficient of component i in a mixture can be expressed as[20,29]:

Table 2 Tait equation parameters for 7 molten homopolymers and 4 molten co-polymers

Any appropriate model for excess Gibbs energy can be used in connection with the above equations to determine the fugacity coefficient and Henry's constants.In this study,the Wilson's equation is used.This equation contains just two adjustable parameters for a binary system(Λ12and Λ21),and is written as:

For in finite dilution,the above equation becomes:

Note that Λ12and Λ21must always be positive numbers.The temperature dependence of these parameters is given by:

whereVjandViare the molar volumes at temperature T of pure polymer j and solvent i.βijand βjiare the interaction energies between the molecules designated in the subscripts.To a fair approximation,these parameters are independent of temperature.For accurate work,βijand βjishould be considered temperature-dependent but in some cases this dependence can be neglected without serious error[21].In this work,two approaches for determination of activity coefficients are compared.In terms of temperature-dependence,a linear dependency on temperature is considered for βijand βjias follows:

4.Results and Discussion

In order to determine the values of the segment parameters amm,bmand cmof PCOR EOS,the following procedure was followed for each polymer:

(1)Initial values for the segment parameters were guessed.

(2)Using Eq.(1)the specific volumes of segments(Vcalc)were calculated for each experimental pressure at a specified temperature.The regression was accomplished by using an optimization program.Parameter values for PCOR equation of state were determined by minimizing the following objective function(OF):

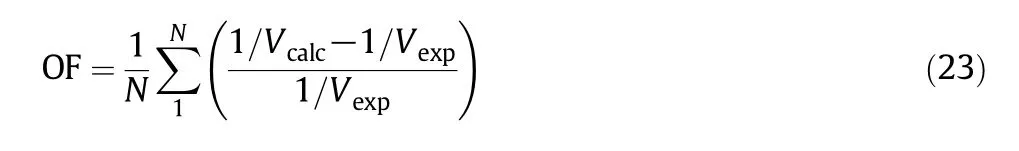
where Vexpis the obtained specific volume of Tait equation in every iteration and N is the number of data points related to each pressure and temperature.

When the objective function was minimized,the values of segment parameters were obtained.The values of bmand cmwere fixed and the values of attraction term,amm,at each temperature were obtain from Eq.(2)with d1,d2,d3and d4as constants.

The obtained values of the PCOR EOS parameters and the absolute average deviation(AAD)of 11 components in this work are listed in Table 3.According to Table 3,the average absolute deviation between the experimental and calculated volume are below 0.14%for PCOR EOS.Therefore,the proposed relationship for energy parameter,amm,is quite adequate to express the behavior of these 7 homopolymers and 4 co-polymers over the specified temperatures and pressures.Figs.1 and 2 show the V-P diagrams for the systems considered in this study at specified temperatures.

5.Prediction of Henry's Constant

In order to determine the Henry's constant the following procedure is used for each polymer:

(1)Considering Eqs.(16),(17),(20)and(21),the parameters a,b,and V for solvent and polymer(hereafter the subscript 1 denotes the solvent and subscript 2 denotes the polymer)are required.The parameters a1,b1and V1of pure solvent are estimated in the classical way,i.e.using an equation of state like Peng-Robinson and van der Waals.[28].In this work,the PR EOS is used.

Table 3 PCOR equation of state parameters for 7 homopolymers and 4 co-polymers melts using the method proposed in this study

(2)For polymer,the parameters a2,b2and V2are determined in a different manner using the procedure outlined earlier as the critical properties are not known for polymers.

(3)Using Eqs.(16)to(18)and(19)to(22),the Henry's constants are calculated and compared with experimental mass fraction Henry's constant data[22-27]at each specified temperature.The regression is accomplished using a Matlab optimization program.The values I12,0,I12,1,I21,0and I21,1in terms of temperature-dependent interaction parameters and constants β12and β21in terms of temperature-independent interaction parameters for PCOR/Wilson's equation are determined by minimizing the following objective function:

where Hcalcand Hexpare the calculated and experimental mass fraction Henry's constants,respectively.The relation between the mole fraction based Henry's constant and the mass fraction based Henry's constant is as follows:

where M1and M2are the molecular weight(MW)of solvent and polymer,respectively.Considering the above procedure,the optimized parameter values and the absolute average deviations of 28 polymer/solvent systems are listed in Table 4 in terms of T-dependent interaction parameters given by Eqs.(21)and(22),and in Table 5 in terms of T-independent interaction parameters.

According to Tables 4 and 5,satisfactory results are obtained by the proposed method(coupled PCOR/Wilson)for prediction of Henry's constant for polymer containing systems,especially in the presence of liquid solvents.The maximum AAD corresponds to mixtures containing gases(i.e.CO2,ethane and ethylene)and when the assumption of constant interaction parameters β12and β21inEq.(20)is implemented.Therefore,the best results are obtained when Eqs.(21)and(22)are used for evaluating parameters β12and β21.Figs.3 to 6 show the results of Henry's constants for solutions containing polymers LDPE,PVAc,PS and PDMS,respectively.

Typical results for Henry's constants in terms of temperature dependent interaction parameters β12and β21are shown in Fig.7 for LDPE/solvent systems.The average AAD for this system is 0.426 while the average AAD for LDPE/solvent with constant β12and β21is 6.227 indicating that the accuracy of PCOR EOS coupled with Wilson's equation with T-dependent interaction parameters is much better compared with the PCOR/Wilson's equation with T-independent interaction parameters.In Table 6,the AAD of the proposed method is compared with those for the three activity coefficient models(Entropic-FV,UNIFAC and UNIFAC-FV)and two equations of state(GC-Flory and van derWaals).The results show that the proposed method has better accuracy compared with other models.

Fig.1.V-P diagram for HDPE,PET,SAN40,SMMA20 and EVA25 polymers.Symbols and lines represent the experimental points and the calculated values,respectively.□Vexpof HDPE at T=177 °C,▬ Vcalcof HDPE at T=177 °C;◊ Vexpof PET at T=282 °C,▬ - ▬Vcalcof PET at T=282 °C;∇Vexpof SAN40 at T=119 °C,▬ --▬ Vcalcof SAN40 at T=119°C;*Vexpof SMMA20 at T=128 °C,▬ ▬ ▬ Vcalcof SMMA20 at T=128°C;○ Vexpof EVA25 at T=110 °C,----Vcalcof EVA25 at T=110 °C.

Fig.2.V-P diagram for LDPE,PVAc,a-PP,PDMS,PS and EP50 polymers.Symbols and lines represent the experimental points and the calculated values,respectively.◊Vexpof LDPEat T=1270°C,▬ Vcalcof LDPEatT=1270°C;□Vexpof PVAcatT=420°C,▬ - ▬Vcalcof PVAc at T=420 °C;∇Vexpa-PP at T=850 °C,▬ ▬ ▬ Vcalca-PP at T=850 °C;Δ Vexpof PDMS at T=300°C,----Vcalcof PDMSatT=300°C;*Vexpof PSatT=1420 °C,······ Vcalcof PSat T=1420°C;○ Vexpof EP50 at T=1770 °C;▬ --▬ Vcalcof EP50 at T=1770 °C.

Table 4 Interaction parameters of polymer/solvent systems(T-dependent assumption for β12& β21)

Table 5 Interaction parameters of polymer/solvent systems(T-independent assumption for β12& β21)

6.Conclusions

The PCOR EOS coupled with the Wilson's equation has been extended to predict Henry's constants of liquids and gases in polymers using the MHV1 mixing rule,the experimental molar volumes correlated by Tait equation and the experimental Henry's constants from literatures.The Wilson's equation was applied as GEmodel in this approach.For all polymers considered in this study,the PCOR/Wilson method showed satisfactory predictions,which were better than five previous models(van der Waals,GC-Flory,UNIFAC,UNIFAC-FV and Entropic-FV).The results also indicated that the accuracy of the PCOR/Wilson method with T-dependent interaction parameters of Wilson's equation(β12and β21)was better than the PCOR/Wilson method with constant interaction parameters.

Fig.3.Experimental and calculated fraction based Henry's constants vs.temperature for LDPE/solvent system using the PCOR/Wilson method(interaction parameters of Wilson's equation are constant).∇Vexpof LDPE/benzene,▬ Hcalcof LDPE/benzene;○Hexpof LDPE/ethylene,▬·▬Hcalcof LDPE/ethylene;ΔHexpofLDPE/n-octane,▬--▬ Hcalcof LDPE/n-octane;*Hexpof LDPE/n-hexane ▬ ---▬ Hcalcof LDPE/n-hexane;+Hexpof LDPE/toluene,······Hcalc of LDPE/toluene;□Hexpof LDPE/vinylacetate,▬ ▬ ▬ Hcalcof LDPE/vinylacetate;◊Hexpof LDPE/n-butane,----Hcalcof LDPE/n-butane.

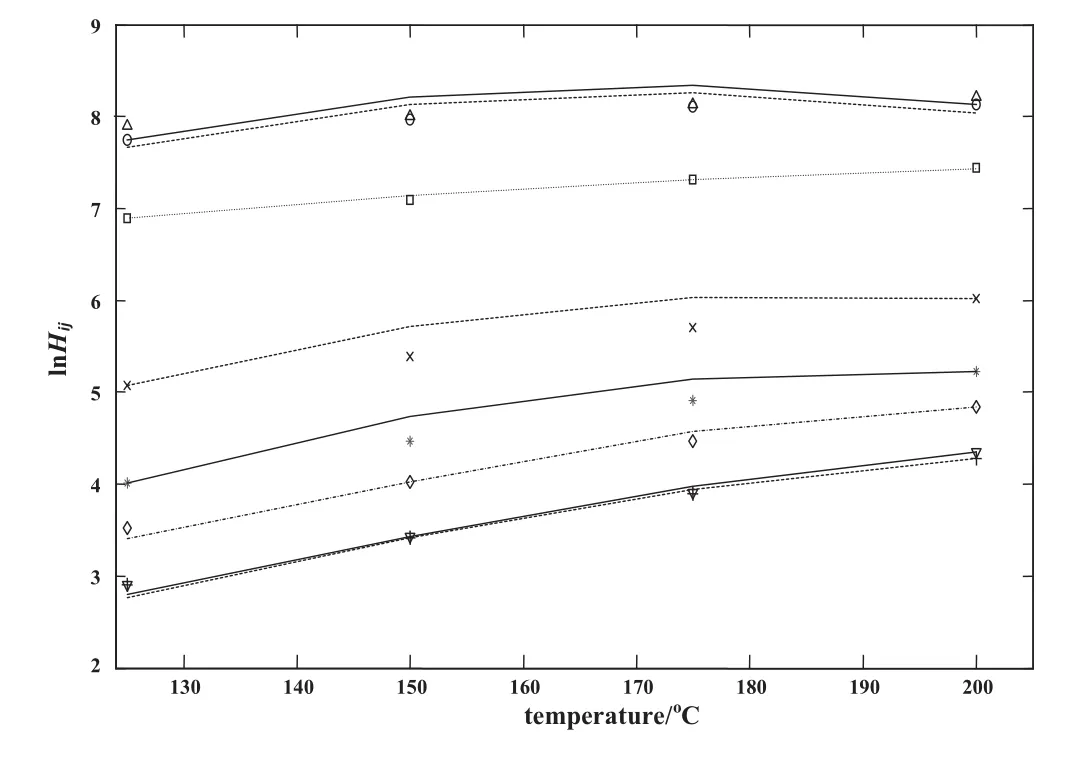
Fig.4.Experimental and calculated fraction based Henry's constants vs.temperature for PVAc/solvent system using the PCOR/Wilson method(interaction parameters of Wilson's equation are constant).+Hexpof PVAc/methylethylketone,▬ ▬ ▬Hcalcof PVAc/methylethylketone;◊Hexpof PVAc/acetone,▬ -▬ Hcalcof PVAc/acetone;○ Hexpof PVAc/ethylene,▬ Hcalcof PVAc/ethylene;□ Hexpof PVAc/CO2,----Hcalcof PVAc/CO2;Δ Hexp of PVAc/ethane,▬ --▬ Hcalcof PVAc/ethane;∇Hexpof PVAc/vinylacetate,▬ ---▬ Hcalc of PVAc/vinylacetate;*Hexpof PVAc/sulfur dioxide,······ Hcalcof PVAc/sulfur dioxide;×Hexpof PVAc/methylchloride,▬---▬ Hcalcof PVAc/methylchloride.

Nomenclature

AAD average absolute deviation,%

a van der Waals attractive force;a segment parameter,cm6·MPa·mol-2

B(T) The Tait parameter,MPa

b exclusion volume;a segment parameter,cm3·mol-1

C universal constant in Eq.(6)equal 0.0894

c effective degree of freedom;a segment parameter

d1adjustable parameter of attraction force,cm6·MPa·mol-2

d2adjustable parameters of attraction force

Fig.5.Experimental and calculated fraction based Henry's constants vs.temperature for PS/solvent system using the PCOR/Wilson method(interaction parameters of Wilson's equation are constant).◊Hexpof PS/R11,▬ -▬ Hcalcof PS/R11;Δ Hexpof PS/R12,▬ --▬Hcalcof PS/R12;*Hexpof PS/R22,······ Hcalcof PS/R22;∇Hexpof PS/propane,▬ ---▬ Hcalc of PS/propane;□Hexpof PS/n-Pentane,▬----▬ Hcalcof PS/n-Pentane;×Hexpof PS/isobutene,----Hcalcof PS/isobutane;+Hexpof PS/n-hexane,▬▬ Hcalcof PS/nhexane;○Hexpof PS/benzene,▬ ▬ ▬ Hcalcof PS/benzene.

Fig.6.Experimental and calculated fraction based Henry's constants vs.temperature for PDMS/solvent system using the PCOR/Wilson method(interaction parameters of Wilson's equation are constant).*Hexpof PDMS/n-pentane,▬ Hcalcof PDMS/n-pentane;○ Hexpof PS/n-hexane,▬ -▬ Hcalcof PS/n-hexane;□ Hexpof PDMS/ethylbenzene,······ Hcalcof PDMS/ethylbenzene;∇Hexpof n-heptane,▬--▬ Hcalcof n-heptane;◊ Hexpof PDMS/n-octane,▬---▬ Hcalcof PDMS/n-octane.

d3adjustable parameter of attraction force,K-1

GEexcess-Gibbs-energy parameter

H Henry's constant

I constant of interaction energy used in Eqs.(23)and(24)

Iijinteraction parameter

M molecular weight,g·mol-1

m parameter in the PR EOS

N number of experiment points

OF objective function

P pressure,MPa

q1EOS-dependent parameter which was set to-0.64663

R universal gas constant,8.314 cm3·MPa·mol-1·K-1

r number of segments in a polymer chain;a segment parameter

T temperature,K

t temperature,°C

V specific volume,cm3·mol-1

V(0,T) the zero-pressure isotherm in the Tait equation,cm3·g-1

y packing factor equal to bm/4υ

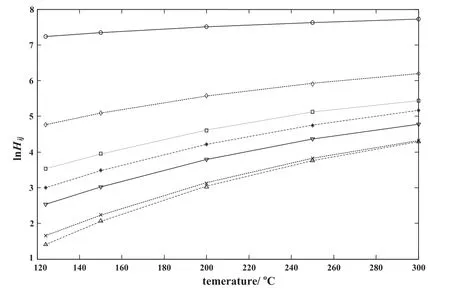
Fig.7.Experimental and calculated fraction based Henry's constants vs.temperature for LDPE/solvent system using the PCOR/Wilson method(interaction parameters of Wilson's equation are T-dependent).∇Hexpof LDPE/Benzene,▬ Hcalcof LDPE/benzene;○ Hexpof LDPE/ethylene,▬-▬ Hcalcof LDPE/ethylene;Δ Hexpof LDPE/n-octane,▬--▬ Hcalcof LDPE/n-octane;*Hexpof LDPE/n-hexane,▬ ---▬ Hcalcof LDPE/n-hexane;×Hexpof LDPE/toluene,······ Hcalcof LDPE/toluene;□ Hexpof LDPE/vinylacetate,▬ ▬ ▬ Hcalcof LDPE/vinylacetate;◊Hexpof LDPE/butane,----Hcalcof LDPE/butane.

Table 6 Absolute average deviations between experimental and calculated Henry's constants for 28 polymer/solute systems③

Z compressibility factor

z mole fraction

α constant equal to 1.078

β interaction energy between the molecules

γ activity coefficient

ε thermal expansion coefficient used in Eq.(7)

Λ interaction parameters for a binary system used in Wilson's equation

λ parameter in the PR EOS

φ fugacity coefficient

ω acentric factor

θ equation of state mixture parameter de fined in Eq.(11)

Subscripts

c critical point

i component 1

j component 2

k dummy index of component 1 and 2

m monomer

mix mixture

p polymer

r reduced property

1 polymer

2 solvent/solute

Acknowledgments

The authors gratefully acknowledge the financial support provided by Islamic Azad University of Mahshahr Branch,Iran.