基于气动参数辨识的飞控系统传感器故障估计

王俭臣，齐晓慧

（军械工程学院无人机工程系，河北石家庄050003）

基于气动参数辨识的飞控系统传感器故障估计

王俭臣，齐晓慧

（军械工程学院无人机工程系，河北石家庄050003）

气动参数的不确定性使得飞行器表现出明显的模型时变特点，此类系统的故障诊断问题是一个难点。以无人机纵向运动为研究对象，提出一种基于气动参数辨识和迭代学习的传感器故障估计方案。将增广容积卡尔曼滤波（ACKF）算法用于气动参数估计，实现飞机模型的在线辨识。故障一旦发生，将辨识得到的气动参数用于局部包络建模，并利用迭代学习算法构造传感器故障估计器。此外，为提高故障的迭代收敛速度，提出一种基于扩张状态观测器（ESO）思想的迭代学习算法。故障仿真实验表明了所提方法的可行性和有效性。

控制科学与技术；传感器故障；飞行控制系统；气动参数；增广容积卡尔曼滤波器；迭代学习；扩张状态观测器

0　引言

由于气动参数在全包络上的不确定性，飞行器具有明显的模型时变性。为实现这类系统的故障诊断，一般需要解决两个问题：一是处理模型时变性，使故障诊断算法兼顾良好的不确定鲁棒性和故障灵敏性；二是设计合适的故障诊断算法。

针对模型时变性，常用的滑模区间、鲁棒性死区等鲁棒技术主要针对系统有限范围内的参数摄动、建模误差等不确定性，对于大范围的系统时变性，这类针对最坏情况的鲁棒性设计将表现出很大的保守性，显著降低诊断灵敏性。对此问题，目前主要采用局部建模方法，例如，文献［1-2］深入研究了采用T-S模糊模型的近空间飞行器的故障诊断与容错方法；文献［3］则在子空间局部线性建模基础上，进一步采用径向基函数（RBF）神经网络补偿系统非线性部分和建模不确定性。

针对故障诊断算法的设计问题，为便于后续的容错控制律设计，故障估计成为近年来的研究热点。目前执行器故障估计问题的研究成果较多，相继提出了自适应观测器［4］、滑模观测器［5］、迭代观测器［6］等方法，而针对传感器故障估计的相关方法还不成熟，一般思路是将传感器故障等效为执行器故障来处理。例如，对一类线性输出结构的非线性系统，文献［7］将传感器故障视为增广状态，在传感器故障导数存在假设下，构建一个神经网络自适应观测器。采用类似处理方法，文献［8］通过求解李雅普诺夫矩阵设计了增广滑模观测器，并能够实现开环不稳定条件下的传感器故障估计。文献［9］则以低通滤波后的系统输出作为新的状态变量，然后构造对不确定性具有鲁棒性的滑模变结构观测器。针对非线性车辆电子稳定性控制系统，文献［10］首先建立对象的T-S模糊化模型，然后采用类似文献［9］的方法引入新的状态变量并设计滑模观测器。在不进行故障等效情况下，文献［11］针对近空间飞行器的T-S模糊模型，采用李雅普诺夫稳定性理论设计了直接估计传感器故障的模糊自适应滑模观测器。

将飞行器建模视为“灰箱”问题，在根据飞行动力学建立模型结构基础上，利用飞行数据进行气动参数辨识成为近年来飞行器设计、建模及控制领域的研究热点［12-15］。相比局部建模方法，该方法具有更好的实时性，同时具有较高的模型辨识精度。但目前该方法在故障诊断领域的应用还不多见。

针对飞控系统的传感器故障估计问题，本文将增广容积卡尔曼滤波（ACKF）算法用于气动参数辨识，以克服系统模型的时变性。针对故障诊断算法的设计问题，基于迭代学习算法的故障估计器具有很高的估计精度［16］，文中将其用于传感器故障问题，通过引入输出误差反馈项构建传感器故障估计器。此外，提出一种扩张状态观测器（ESO）思想的迭代学习算法，以提高故障估计器的收敛速度。

1　问题描述

针对某小型固定翼无人机模型［17］，其水平无侧滑条件下的纵向运动方程为：俯仰速率微分方程

空速微分方程

攻角微分方程

俯仰角微分方程

式中：h1～h4，g11、g22、g32分别表示下文（9）式中系统状态模型中向量函数h（）和g（）的相应元素。

表1　无人机参数及变量Tab.1 Parameters and variables of airplane

假设系统的4个状态量均可传感器测量，在考虑过程扰动ηx、测量噪声ηy以及传感器故障情况下，系统（5）式～（8）式具有如下的非线性形式：

式中：θc为气动参数向量；u为控制输入，包括升降舵偏角δe和发动机推力FT；fs为传感器故障。

2　气动参数在线辨识

将（9）式中的气动参数向量θc扩展为状态向量

然后引入状态辅助方程

在不考虑传感器故障情况下，状态增广后的系统方程为

在状态增广基础上，可采用容积卡尔曼滤波（CKF）算法实现模型状态和不确定气动参数的联合估计。CKF算法采用数值积分方法直接计算非线性变换后随机变量的均值和协方差，具有比扩展卡尔曼（EKF）和不敏卡尔曼（UKF）算法更好的非线性逼近能力、数值精度及滤波稳定性［18］；而相比粒子滤波（PF）算法，其计算量明显降低，且不存在粒子贫化问题。基于ACKF算法的状态和气动参数联合估计过程可描述为：

1）按照（10）式和（11）式得到气动参数增广后的系统模型（12）式和（13）式，并对模型近似离散化。确定初始状态估计值^x0|0和协方差阵P0|0，其中

2）时间更新。

第1步 计算容积点

式中：i=1，2，…m，m=2nx，nx为状态维数；参数ξi的计算公式为

式中：ei为第i个元素为1、其余元素为0的基本单位向量。

第2步 通过增广系统状态方程传播容积点

式中：F（·）表示（12）式的增广系统状态方程。

第3步 计算状态一步预测值

第4步 计算预测误差方差阵

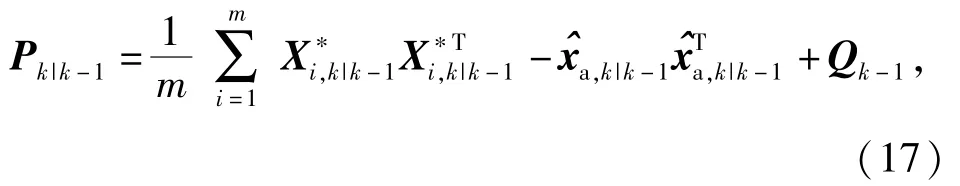
式中：Qk-1表示k-1时刻的过程噪声方差阵。

3）量测更新。

第1步 计算容积点

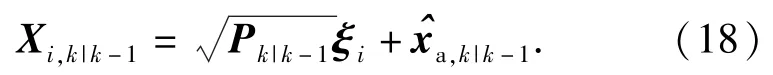
第2步 传播容积点

第3步 计算量测预测值

第4步 计算新息协方差阵

式中：Rk表示k时刻测量噪声方差阵。

第5步 计算互协方差阵

第6步 计算增益阵

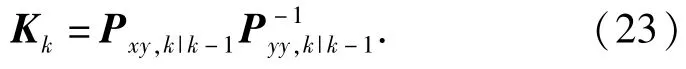
第7步 更新状态估计量

第8步 计算误差协方差阵

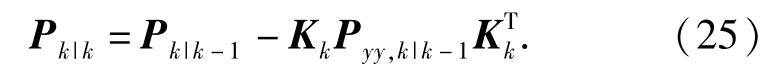
3　基于迭代学习的传感器故障估计

3.1传感器故障估计器设计

迭代学习故障估计器是近年提出的一种新方法，它通过在观测器中引入一个虚拟故障参数值，并进行反复迭代，最终可实现故障的完全跟踪估计。相比其他故障估计方法，迭代学习方法以可承受的计算代价获得更高的故障估计精度。文献［16］采用迭代学习故障估计器研究了系统状态方程中的故障估计问题，本文将该方法用于飞控系统的传感器故障估计问题。假设某时刻由ACKF算法得到的气动参数估计值为，一旦故障发生，则近似当前局部包络上气动参数保持不变，然后通过引入输出误差反馈项构建如下基于迭代学习的开环P型传感器故障估计器

为保证（26）式的传感器故障估计器学习过程收敛，给出如下假设条件：

假设1 系统过程扰动及测量噪声ηx、ηy是有界的。

假设4 系统方程的非线性部分满足Lipschitz条件，即‖α（x1，θc）-α（x2，θc）‖≤γ1‖x1-x2‖，‖g（x1，θc）u-g（x2，θc）u‖≤γ2‖x1-x2‖.需要指出，本文所研究系统满足局部Lipschitz条件。

定理1 在假设1～假设5基础上，对于（26）式的故障估计器，若开环P型学习律的增益矩阵Γ满足‖I-Γ‖＜1，则估计器的故障估计误差可收敛到一个有界邻域，且该邻域大小与以及Γ有关。

定理证明可参考文献［19］的第6章内容，此处限于篇幅，证明过程略。

3.2采用扩张状态观测器思想的迭代学习算法

为进一步提高上述故障估计器的迭代收敛速度，借鉴自抗扰控制中的扩张状态观测器（ESO）设计思想。该方法利用适当的输出误差非线性反馈可同时实现系统状态和未知扰动的快速跟踪估计，具有比误差线性反馈更好的动态特性。由此启发，本文将ESO中的非线性反馈设计从时间轴类推到迭代轴，从而提出一种ESO迭代学习算法。

首先考虑如下的2阶系统

式中：w（t）为系统未知部分，如建模不确定性或外扰；b为控制输入增益；u（t）为控制输入。将系统未知部分扩展为新的状态x3=w（t），然后可设计如下扩张状态观测器

式中：z1、z2、z3分别是观测器状态；β01、β02、β03为适当参数；gi（e），i=1，2，3，是满足条件egi（e）＞0的适当非线性函数。利用上述观测器就能很好地跟踪估计系统状态x1、x2和未知部分w（t），即有：z1→x1，z2→x2，z3→x3=w（t）.一般地，gi（e）可取g1（e）=e，g2（e）=fal（e，1/2，δ），g3（e）=fal（e，1/4，δ），其中

式中：sign（e）为符号函数。

上述ESO是时间轴上的观测器输出误差处理过程。将该过程类比到迭代轴，可得如下的传感器故障估计器

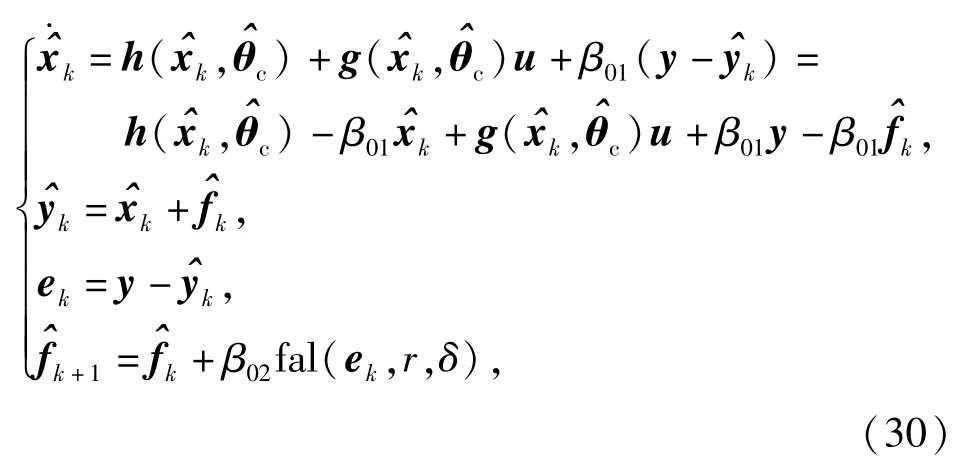
式中：参数β01、β02按照2ω、ω2的规律取值；输出误差向量ek的fal（）函数是指对ek的每个元素取fal（）函数。类比定理1的证明过程，可得如下关于（30）式所示估计器的故障估计收敛性定理。

定理2 在假设1～假设5基础上，对（30）式的故障估计器，若非线性函数fal（ek）使得‖I-M‖＜1，其中：，为对角矩阵；eki，i=1，2，…，n表示ek的第i个元素，n为系统状态维数。估计器的故障估计误差可收敛到一个有界邻域，且该邻域大小与以及Γ有关。

限于篇幅，证明过程略。

4　仿真验证

验证如下飞行控制过程：目标运动状态xgoal=［q，VT，α，θ］=［0，16，0.053 5，0.053 5］；初始运动状态xinit=［q，VT，α，θ］=［0，30，0.042 5，0.042 5］；系统的反馈控制矩阵为

取（12）式和（13）式的增广系统过程噪声协方差矩阵P=10-4diag（［0.01，1，0.01，0.01，0.01，1，4，0.1］），测量噪声协方差矩阵Q=10-4diag（［0.01，1，0.01，0.01］），初始状态协方差P0|0= 0.1I8.无故障情况下，采用ACKF算法获得的气动参数的辨识效果如图1所示。结果表明，该算法能够较精确地跟踪估计气动参数的变化。

图1　无故障时气动参数辨识结果Fig.1 Identified results of aerodynamic parameters under normal condition

4.1故障估计实验

在气动参数辨识基础上，按照（30）式建立传感器故障估计器，其中故障检测阈值Td=［0.2，0.6，0.1，0.05］T，优化时域长度P=0.1 s，残差阈值ε= 0.001，非线性反馈函数g2（ek）=fal（ek，1/2，0.01），可调参数ω=3.5.分别给系统加入如下的单一型和并发型传感器故障。

单一故障

并发故障

单一型传感器故障设置为空速值测量恒偏差故障，其估计效果如图2所示。仿真过程中气动参数及其估计值的变化如图3所示。图2结果显示，采用迭代学习机制的故障估计方法能够准确估计出所注入故障，具有相当高的故障估计精度。但估计结果局部放大显示，该方法仍存在一定误差。根据定理2分析可知，在本文所研究对象存在模型误差和状态初值偏差情况下，所设计迭代学习故障估计器的估计误差只能收敛到一个小的误差范围内。

图2 单一型故障估计结果Fig.2 Estimated result of single fault

图3的实验结果则表明，在故障估计的有限时间范围内，近似认为气动参数保持不变是可行的，不会引入明显的参数误差（即模型误差）。一旦故障估计过程结束，则采用ACKF滤波算法重新进行参数估计，由图3的结果看到，ACKF算法重启时会产生明显的参数估计误差，但误差会逐渐减小。

在单一型故障实验基础上，进一步验证本文方法对并发型故障的估计性能。所采用并发型传感器故障包括空速值测量恒偏差故障和俯仰角测量正弦偏差故障，所得实验结果如图4所示。实验结果表明，本文方法对并发型故障仍具有较高的故障估计精度。

图3　故障时气动参数辨识结果Fig.3 Identified results of aerodynamic parameters under fault condition

图4　并发型故障估计结果Fig.4 Estimated results of concurrent fault

4.2迭代学习算法比较

为比较说明本文所提出的ESO迭代学习算法的性能，将传统开环P型迭代学习算法用于故障估计实验，分别设置迭代学习增益Γ=0.3，Γ=0.5.仿真采用如下的俯仰角传感器故障：

图5给出了两种算法在第一个迭代优化时域上的故障估计误差收敛曲线。对比Γ=0.3，Γ=0.5两种P型学习算法看出，学习增益变大，故障估计器的收敛速度加快。但根据迭代学习控制理论［19］，过大的学习增益可能导致学习过程发散，即迭代学习算法的稳定性会降低。而对于本文学习算法，由所采用的fal（）函数可知，算法前期采用较小的学习增益，可保证学习算法的稳定性；而算法后期增益变大，以获得较快的收敛速度。图5的仿真结果显示本文算法的总体收敛速度最快。

图5　同一优化时域上的估计误差收敛曲线Fig.5 Convergence curves of estimation errors at the same optimization time domain

5　结论

以无人机纵向运动模型为研究对象，讨论了基于气动参数辨识和迭代学习估计器的飞控系统传感器故障估计方法。主要结论如下：

1）采用ACKF算法实现参数时变系统的在线辨识，相比局部建模方法具有更好的实时性，而且不需要参数变化的先验知识。

2）通过引入输出误差反馈项，将迭代学习估计器用于传感器故障估计；此外，将ESO思想引入到迭代轴，得到一种改进的迭代学习算法。

3）仿真实验表明，所提出的方法能够较精确地估计出飞控系统的传感器故障，同时具有处理并发故障能力；所提出的ESO迭代学习算法具有比传统P型算法更快的收敛速度。

（

）

［1］Zhang K，Jiang B，Shi P.Fault estimation observer design for discrete-time Takagi-Sugeno fuzzy systems based on piecewise Lyapunov functions［J］.IEEE Transactions on Fuzzy Systems，2012，20（1）：192-200.

［2］Gao Z F，Jiang B，Shi P，et al.Fault-tolerant control for a near space vehicle with a stuck actuator fault based on a Takagi-Sugeno fuzzy model［J］.Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2010，24（5）：587-598.

［3］Zhang Z D，Hu S S.A new method for fault prediction of modelunknown nonlinear system［J］.Journal of the Franklin Institute，2008，345（2）：136-153.

［4］Zhang X D，Polycarpou M M，Parisini P.Fault diagnosis of a class of nonlinear uncertain systems with Lipschitz nonlinearities using adaptive estimation［J］.Automatica，2010，46（2）：290-299.

［5］Tan C P，Edwards C.Robust fault reconstruction in uncertain linear systems using multiple sliding mode observers in cascade［J］. IEEE Transactions on Automatic Control，2010，55（4）：855-880.

［6］Wu Q，Mehrdad S.Robust fault diagnosis of a satellite system using a learning strategy and second order sliding mode observer［J］.IEEE Systems Journal，2010，4（1）：112-121.

［7］贾明兴，王福利，何大阔.基于RBF神经网络的传感器非线性故障鲁棒诊断［J］.东北大学学报：自然科学版，2004，25（8）：719-722. JIA Ming-xing，WANG Fu-li，HE Da-kuo.Robust nonlinear fault diagnosis for sensors based on RBF neural network［J］.Journal of Northeastern University：Natural Science，2004，25（8）：719-722.（in Chinese）

［8］Alwi H，Edwards C，Tan C P.Sliding mode estimation schemes for incipient sensor faults［J］.Automatica，2009，45（7）：1679-1685.

［9］何静，邱静，张昌凡.基于观测器的传感器故障重构方法及其应用［J］.兵工学报，2009，30（6）：672-676. HE Jing，QIU Jing，ZHANG Chang-fan.Observer-based sensor fault reconstruction method and its application［J］.Acta Armamentarii，2009，30（6）：672-676.（in Chinese）

［10］于金泳，刘志远，陈虹.基于滑模观测器的车辆电子稳定性控制系统故障重构［J］.控制理论与应用，2009，26（10）：1057-1063. YU Jin-yong，LIU Zhi-yuan，CHEN Hong.Fault reconstruction in the vehicle electronic stability control based on sliding mode observers［J］.Control Theory&Applications，2009，26（10）：1057-1063.（in Chinese）

［11］Shen Q，Jiang B，Cocquempot V.Fault diagnosis and estimation for near-space hypersonic vehicle with sensor faults［J］.Proceedings ofthe Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2011，226（3）：302-312.

［12］Pashilkar A A，Kamali C，Raol J R.Direct estimation nonlinear aerodynamic coefficients［C］∥AIAA Atmospheric Flight Mechanics Conference and Exhibit.Hilton Head，South Carolina：AIAA，2007.

［13］刘毅男，张胜修，曹立佳，等.基于气动特性辨识的折叠翼飞行器可重构控制系统设计［J］.系统工程与电子技术，2013，35（5）：1037-1044. LIU Yi-nan，ZHANG Sheng-xiu，CAO Li-jia，et al.Reconfigurable flight control system design for folding-wing air vehicles based on aerodynamic characteristics identification［J］.Systems Engineering and Electronic，2013，35（5）：1037-1044.（in Chinese）

［14］吴伟，陈仁良.直升机悬停状态全耦合飞行动力学模型辨识方法［J］.航空学报，2011，32（2）：202-211. WU Wei，CHEN Ren-liang.Identification method for helicopter fully coupled flight dynamics model in hover condition［J］.Acta Aeronautica et Astronautica Sinica，2011，32（2）：202-211.（in Chinese）

［15］余舜京，程艳青，钱炜祺.跨声速气动参数在线辨识方法研究［J］.宇航学报，2011，32（6）：1211-1216. YU Shun-jing，CHENG Yan-qing，QIAN Wei-qi.Research on transonic aerodynamic parameter online identification［J］.Journal of Astronautics，2011，32（6）：1211-1216.（in Chinese）

［16］颜秉勇，田作华，施颂椒，等.基于故障跟踪估计器的非线性时滞系统故障诊断［J］.控制与决策，2009，24（1）：133-136. YAN Bin-yong，TIAN Zuo-hua，SHI Song-jiao，et al.Fault diagnosis for nonlinear time-delay systems based on fault tracking approximator［J］.Control and Decision，2009，24（1）：133-136.（in Chinese）

［17］Ducard G J J.Fault-tolerant flight control and guidance systems：practical methods for small unmanned aerial vehicles［M］.London：Springer-Verlag，2009.

［18］孙枫，唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较［J］.控制与决策，2013，28（2）：303-308. SUN Feng，TANG Li-jun.Estimation precision comparison of cubature Kalman filter and unscented Kalman filter［J］.Control and Decision，2013，28（2）：303-308.（in Chinese）

［19］林辉，王林.迭代学习控制理论［M］.西安：西北工业大学出版社，1998：1-105. LIN Hui，WANG Lin.Theories of iterative learning control［M］. Xi'an：Northwestern Polytechnic University Press，1998：1-105.（in Chinese）

Sensor Fault Estimation Method for Flight Control Systems Based on Aerodynamic Parameter Identification

WANG Jian-chen，QI Xiao-hui
（Department of Unmanned Plane Engineering，Ordnance Engineering College，Shijiazhuang 050003，Hebei，China）

The aircraft model shows obvious time-varying characteristic due to the uncertainty of aerodynamic parameters.The fault diagnosis of the flight control systems is a difficult issue.A sensor fault estimation approach based on aerodynamic parameter identification and iterative learning is proposed by taking the longitudinal motion model of some unmanned aerial vehicle as the study subject.The augmented cubature Kalman filter（ACKF）is used for the aerodynamic parameter estimation so that the system model can be identified online.Once a fault comes up，the currently identified aerodynamic parameters are applied to system modeling in the local flight envelope，and a fault estimator is constructed using the iterative learning algorithm.Furthermore，a novel iterative learning algorithm based on the essence of extended state observer（ESO）is designed to improve the fault estimation speed.The fault simulation experiments are conducted to verify the feasibility and effectiveness of the proposed approach.

control science and technology；sensor fault；flight control system；aerodynamic parameter；augmented cubature Kalman filter；iterative learning；extended state observer

TP273

A

1000-1093（2015）01-0103-08

10.3969/j.issn.1000-1093.2015.01.015

2014-03-03

武器装备预先研究重点基金项目（9140A27020211JB3402）

王俭臣（1987—），男，博士研究生。E-mail：lichen197@163.com；齐晓慧（1962—），女，教授，博士生导师。E-mail：qi_xh@163.com