轴向载荷对大长细比导弹稳定性的影响研究

全景阁，叶正寅，张伟伟

（西北工业大学翼型叶栅空气动力学国家重点实验室，陕西西安710072）

轴向载荷对大长细比导弹稳定性的影响研究

全景阁，叶正寅，张伟伟

（西北工业大学翼型叶栅空气动力学国家重点实验室，陕西西安710072）

大长细比飞行器的刚性模态和弹性模态极易发生耦合失稳现象。轴向载荷作用下其结构刚度特性会发生变化，进一步降低其稳定性。使用有限元方法分析了大长细比导弹在轴向载荷作用下的结构刚度特性。采用当地流活塞理论计算弹性体变形的气动力，耦合结构运动方程，基于模态坐标在状态空间内实现结构运动方程的特征值分析和时域求解，研究轴向载荷对大长细比导弹稳定性的影响。研究发现：大轴向过载作用下，大长细比导弹的刚性模态和弹性模态将出现耦合失稳，且随着轴向过载的增加，弹体的结构刚度特性下降，失稳速度降低。

兵器科学与技术；大长细比；导弹；当地流活塞理论；轴向载荷；耦合失稳

0　引言

为了满足现代高科技军事战斗中导弹飞行高速度、高机动、大射程的需求，大长细比导弹已成为未来发展的重要趋势。导弹长细比的增加将导致弹体刚度降低、柔度增加，导弹在发射和飞行过程中的柔性变形和弹性振动变得不可忽略。再加上轻型复合材料的使用，使大长细比导弹的弹性效应更加明显。

早在20世纪60年代就有学者开始关注细长体导弹的弹性效应问题，但主要集中在结构振动特性和动力学稳定性问题上。1965年，Beal［1］研究了带简单反馈系统的导弹在常值和脉动推力作用下的动力学稳定性。Ohshima等［2］采用自由梁模型，研究了头部有集中载荷的飞行器在推力作用下的动力学稳定性。Pourtakdoust等［3］研究了变质量导弹在推力作用下的弹体振动特性。国内，宋健［4］在2000年研究了推力和空气阻力对火箭横向振动频率和振型的影响，分析了推力和阻力作用下频率降低的原因。许赟等［5］将弹箭飞行器简化为非均匀梁模型，用有限元方法分析了细长弹箭在随动推力作用下的动力学稳定性和结构横向振动特性。研究表明，推力会影响弹箭结构的横向振动频率和振型特性，影响动力学稳定性。

近年来，国内外学者针对大长细比导弹的气动弹性问题［6-8］与伺服气动弹性问题［9-11］开展了大量的研究。王良明［6］从弹箭空间摆动和弹性振动耦合的动力学模型出发，利用拉普拉斯变换方程对细长弹箭的气动弹性静态和动态稳定性进行了研究。吴小胜等［7］采用动网格技术，一体化求解非定常N-S方程、结构变形方程及角运动方程，分析研究了结构参数和质量偏心对柔性大长细比导弹的弹性运动和角运动的影响。Wu等［8］运用有限元方法和1阶活塞理论，研究了定常推力对细长导弹结构动力学稳定性以及颤振特性的影响。研究表明，大长细比导弹的气动弹性问题不容忽视。

对于常规飞行器，由于刚体运动较缓慢，飞行模态的频率远低于结构模态的频率，故气动弹性分析一般不用考虑飞行模态的影响。而传统飞行力学分析将飞行器视作刚体，不考虑结构弹性变形对飞行模态的影响。因此，从传统意义上讲，气动弹性分析和飞行模态分析是相互独立的。但对于大长细比飞行器，其长细比很大，弹性效应不可忽视。对于一些导弹或火箭，由于特殊的工程需求，轴向过载会很大（超过100 g），结构刚度会随着轴向载荷的增加而降低，弹体受扰后更易发生弹性变形，且随着动压的增加，结构弹性变形会越来越大。弹性变形反过来又会影响飞行器的气动特性，使作用在飞行器上的气动力发生变化，焦点位置前移，导致飞行器的稳定性变差，发生失稳现象。故大长细比导弹的气动弹性分析不能独立于飞行模态分析，飞行模态分析也不能独立于气动弹性分析，二者要统一起来，进行整体、系统地分析。

本文首先利用有限元方法分析得到大长细比导弹在轴向载荷作用下的结构振动特性。然后采用基于计算流体力学（CFD）的当地流活塞理论方法，基于结构模态坐标在状态空间内耦合结构动力学方程和气动力模型，通过特征值分析和数值求解方法获得大长细比导弹的稳定性特性，研究轴向过载对大长细比导弹刚性模态与弹性模态耦合失稳问题的影响。

1　研究方法

20世纪90年代初，国内的陈劲松等［12］、杨炳渊等［13］提出了当地流活塞理论，该方法对尖前缘薄翼型的超音速大迎角问题有较好适应性，但仍存在一定的局限性。Zhang等［14］、张陈安等［15-16］借鉴其思路，结合现代CFD技术发展了一种新的当地流活塞理论，并将其应用到超音速、高超音速气动弹性与伺服气动弹性的仿真分析。这种改进的当地流活塞理论对弹头的钝体外形和弹翼的尖薄外形都有很好的适应性，便于系统分析，且在一定范围内具有与非定常Euler方程相当的计算精度，计算效率却高出2个量级。

1.1基于CFD的当地流活塞理论

当地流活塞理论的压力计算公式［14-16］为

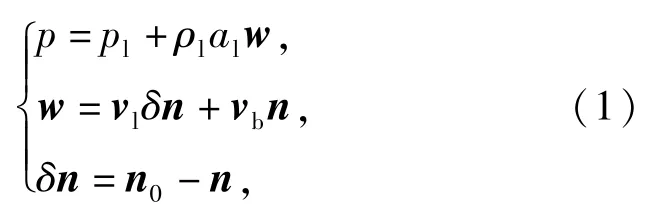
式中：p为物面压强；w为沿物面外法线方向的上洗速度；vb为物面振动速度；vl、pl、ρl和al分别为当地速度、当地压强、当地密度和当地音速；n0为物面变形前的外法线单位矢量；n为物面变形后的外法线单位矢量。

选取模型的N阶结构模态，对应点的第m阶振型以zxm=ami+bmj+cmk的形式给出，对应的广义坐标为ξm（t），从而得到用模态坐标表示的广义气动力［15］

对于一个特定计算状态（马赫数Ma、迎角α），用Euler方程得到定常流场后，［A′］和［B］是确定的。（2）式的基于模态坐标的气动力系数矩阵就可以耦合结构运动方程，进行稳定性分析。

1.2结构运动方程

应用拉格朗日方程，基于模态坐标的结构运动方程可以写为如下形式［15］：

式中：M为质量矩阵；G为结构阻尼矩阵（这里令G= 0）；K为刚度矩阵；Q为广义气动力。把（2）式代入（3）式得

引入结构状态变量

则（4）式可以写成

式中：

给定Ma∞、ρ∞、v∞，则C为一实矩阵，这样系统的稳定性分析就转化为求解状态方程中矩阵C的特征值问题。计算不同速度下矩阵C的特征值。当所有特征值的实部均小于0时，系统将处于稳定状态。当某一特征值的实部等于0时，系统处于临界稳定状态。当某一特征值的实部大于0时，系统处于不稳定状态，如果此时该特征值的虚部降为0，则系统表现为静态失稳；如果特征值的虚部不为0，则系统表现为动态失稳。

对（4）式，除了引入状态空间变量求解矩阵的特征值外，还可以用数值方法进行求解。当Ma∞、ρ∞、v∞一定时，（5）式就变成1阶常微分方程组，可以使用常微分方程的数值解法进行求解，得到各阶模态坐标随时间变化的时域响应曲线。计算不同速度下各阶模态坐标的时域响应曲线，就可根据响应历程随时间变化的特征来进行稳定性判断。在某一速度下，如果各阶模态坐标的时域响应曲线趋于收敛，则表示系统处于稳定状态；如果时域响应曲线发散，则表示系统处于不稳定状态；如果时域响应曲线趋于稳定，则表示系统处于临界稳定状态。

1.3流程图

采用当地流活塞理论，耦合结构运动方程，基于模态坐标进行稳定性分析的详细步骤可以用图1的流程图表示。

图1　当地流活塞理论稳定性分析流程图Fig.1 Flow chart for analysis of system stability based on local piston theory

对于给定的气动外形，只要已知了计算状态和结构参数，按照图1的计算流程，就可以进行相关的静稳定性及动稳定性分析。

2　算例与分析

进行系统稳定性分析时，结构刚度特性的变化会对分析结果造成很大的影响，所以分析轴向载荷对结构刚度特性的影响是很有必要的。首先针对典型的细长铝杆结构，研究其在不同轴向载荷作用下的结构刚度特性变化，总结出一般规律。而后针对给定的弹体结构，建立等价的结构有限元模型，计算大轴向过载下，轴向载荷对弹体结构刚度特性的影响，进而在该刚度特性的基础上开展大长细比导弹的稳定性分析。

2.1细长压杆受轴向载荷作用时的刚度特性分析

实际工程中，细长压杆作为承重构件，常常由于压力的增大而发生受压失稳现象，使杆件变弯失去承载能力。在压杆受压失稳前，轴向压力的增加，会导致压杆的刚度特性发生变化。以两端自由的细杆为例来分析说明细长压杆在不同轴向载荷作用下的刚度特性变化。

细杆长1 m，横截面为半径5 mm的圆，材料为铝合金。几何模型如图2所示。

图2　两端自由细杆几何模型图Fig.2 Geometry model of slender rod

利用有限元分析软件MSC/NASTRAN进行计算分析。通过施加不同的轴向惯性加速度来实现轴向均布惯性载荷的变化，故进行数据分析时，用轴向加速度来表征轴向惯性力的变化。轴向加速度为100 g指的是轴向加速度a=100×重力加速度g，依次类推。

图3给出了两端自由细杆前3阶模态固有频率随轴向压力的变化曲线。由图3可以看出，随着轴向载荷的增大，细杆的刚度特性呈下降趋势，相应的固有频率也随着降低。其中，杆的1阶固有频率变化比较明显，2阶和3阶固有频率虽然也呈线性下降趋势，但降低的幅度不大。

图3　不同轴向载荷作用下细杆前3阶模态固有频率随轴向力的变化曲线Fig.3 Mode frequencies of slender rod under different axial loades

当杆的轴向压力增大到一定程度，杆的1阶固有频率降为0，杆处于临界失稳状态，此时的轴向压力称为杆的临界压力。当杆的轴向压力超过临界压力时，杆就发生屈曲失稳了。计算得到杆临界失稳时的轴向加速度约为423.51 g.

图4给出了不同轴向惯性载荷下杆的前3阶模态振型图。由图4可以看出，随着轴向惯性载荷的增加，杆的1阶振型发生了显著的变化，但2阶和3阶振型变化甚微。

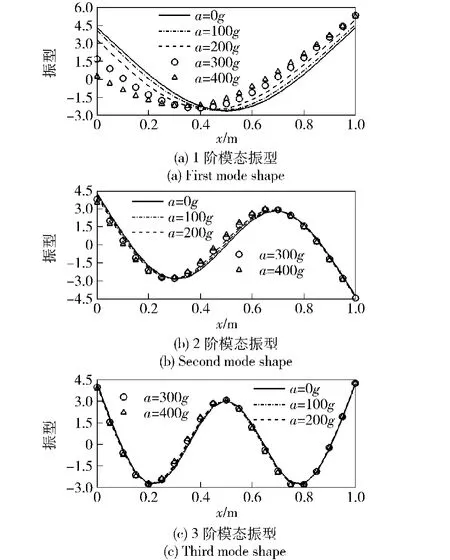
图4　细杆在不同轴向载荷下的前3阶模态振型对比图Fig.4 Three mode shapes of slender rod under different axial loades

2.2大长细比导弹受轴向载荷作用时的刚度特性分析

由细长压杆刚度特性分析可知，对于大长细比导弹，弹身轴向施加不同的惯性力时，其刚度特性会发生变化。接下来，就针对大长细比导弹，进行轴向载荷对弹体结构刚度特性的分析。同上，采用有限元分析软件MSC/NASTRAN进行分析，用轴向惯性加速度来表征惯性力的变化。计算模型采用长细比为20的简易导弹模型，导弹总长3.5 m，弹身直径为0.17 m，几何模型如图5所示。

图6给出了弹体前3阶模态固有频率随轴向载荷的变化曲线。由图6可以看出，随着轴向载荷的增大，弹体的刚度特性呈下降趋势，相应的固有频率也随着降低。

图5　导弹几何模型Fig.5 Geometry model of slender missile

图6　弹体前3阶模态固有频率随轴向载荷的变化曲线Fig.6 Mode frequencies of missile under different axial loads

其中，1阶模态的固有频率变化特性比较显著。随着轴向载荷的增大，弹体的1阶固有频率逐渐降低。当轴向载荷增大到一定程度，弹体的1阶固有频率降为0.此时，弹体处于临界失稳状态，此时的轴向载荷变为弹体的临界载荷。计算得到，轴向加速度约为305.67 g时，弹体的1阶模态固有频率降为0，处于临界失稳状态。

图7给出了不同轴向载荷作用下，弹体的前3阶振型对比图。由图7可以看出，不同的轴向载荷下，弹体的1阶模态振型发生了较大的变化，而2阶模态振型和3阶模态振型相对变化不大。

图7　不同轴向惯性力下弹体的前3阶模态振型对比图Fig.7 Three mode shapes of missile under different axial loads

至此可知，对于大长细比导弹，考虑轴向惯性过载后，弹体的结构刚度特性发生了显著的变化，这必然会影响导弹的稳定性特性分析。

2.3大长细比导弹受轴向载荷作用时的稳定性分析

由2.2节的分析可知，随着轴向载荷增大，结构1阶模态的固有频率变化特性比较明显。表1给出了弹体施加不同轴向过载时，前3阶模态的固有频率。对比发现，考虑100 g轴向过载后，1阶模态的固有频率下降了28.4%.由于该导弹的长细比大，弹性特征明显，大轴向过载下，可能会发生弹性模态与刚性模态的耦合失稳现象。故在接下来的稳定性分析中，考虑了导弹的短周期俯仰模态和弹体的前3阶模态，在结构模态和飞行模态的基础上，系统地分析不同轴向过载下大长细比导弹刚性模态与弹性模态耦合失稳的稳定性问题。

表1　弹体前3阶模态固有频率对比Tab.1 Mode frequencies of missile under different axial loads

使用2.2节分析得到的模态数据，利用第1节讲述的方法，耦合气动力模型和结构动力学方程，进行大长细比导弹稳定性分析。计算状态为：马赫数Ma为3.5，迎角α=0°，基于海平面状态。

图8和图9给出了弹体不施加轴向过载（即0 g）时系统的稳定性分析结果。由图8各阶模态的阻尼系数gd、频率ω和特征根随动压的变化曲线可以看出，不考虑轴向过载时，当速度v∞＞1 644 m/s时俯仰模态率先穿过虚轴，频率降为0，由稳定变为不稳定。这种现象的出现是由于弹性变形改变了全弹的气动载荷分布，使导弹的纵向模态变得不稳定。在进行流-固耦合分析时，单独考虑弹性模态或刚性模态都不会发生失稳，这种不稳定的出现正是弹性模态和刚性模态耦合作用的结果。

图8　无轴向过载时弹体的根轨迹图Fig.8 Root loci of missile（a=0 g）

由图9各阶模态位移ξ随时间的变化历程可以看出，当来流速度v∞=1 500 m/s时，弹体的俯仰模态与前3阶模态响应曲线均趋于收敛，系统处于稳定状态；来流速度v∞=1 680 m/s时，弹体的各阶模态响应曲线明显发散，系统处于不稳定状态；来流速度v∞=1644 m/s时，弹体的各阶模态响应曲线趋于常数，系统处于临界稳定状态。图中俯仰模态的幅值很大，说明结构的弹性变形对俯仰模态产生了较大的影响。

图10和图11给出了弹体施加100 g轴向过载时系统的稳定性分析结果。由图10可以看出，施加100 g轴向过载后，当来流速度v∞＞1 156 m/s时俯仰模态率先穿过虚轴，频率降为0，由稳定变为不稳定。由图11可以看出，当来流速度v∞=1 000 m/s时，弹体的俯仰模态与前3阶模态响应曲线均趋于收敛，系统处于稳定状态；来流速度v∞=1 200 m/s时，弹体的各阶模态响应曲线趋于发散，系统处于不稳定状态；来流速度v∞=1 156 m/s时，弹体的各阶模态响应曲线趋于常数，系统处于临界稳定状态。

相对于不加过载的分析结果，施加100 g轴向过载后，弹体的失稳速度大幅降低。这主要是由于此时结构的1阶模态频率比不加过载时降低了很多，弹体的弹性效应增强，弹性变形对气动载荷分布的影响增加，使导弹纵向稳定性变得更加敏感。施加轴向过载后，临界失稳动压的减小将进一步缩小导弹的飞行包线，安全裕度变得更小了，严重影响导弹在马赫数为3.5状态下的飞行品质。

图12给出了弹体分别施加50 g、200 g轴向过载时系统的稳定性分析结果。图中依然可见弹性变形使俯仰模态变得不稳定的现象。由图12可以看出，弹体施加50 g轴向过载时，弹体在v∞=1 402 m/s时处于临界稳定状态，越过此临界点俯仰模态由稳定变为不稳定，频率降为0.在200 g轴向过载时，弹体在v∞＞828.6 m/s俯仰模态由稳定变为不稳定，频率降为0.

图9　无轴向过载时弹体不同速度下的时域响应曲线Fig.9 Time responses of generalized displacements at various velocities（a=0 g）

表2总结了弹体在不同轴向过载下的稳定性分析结果。对比发现，随着轴向过载的增加，弹体的失稳速度逐渐降低，100 g过载时弹体失稳速度已下降了约30%.这主要是由于随着轴向过载的增加，弹体结构频率降低，弹性效应增强，导弹受扰后会产生更大的弹性变形，弹性变形对弹体俯仰模态的影响加剧，导致系统稳定性变差，失稳速度降低。由此可见，大长细比导弹的稳定性分析需要同时考虑弹性模态和刚性模态，在大轴向过载下，随着结构刚度特性的降低，弹体会发生弹性模态与刚性模态的耦合失稳。故大长细比导弹的稳定性分析不可忽视轴向载荷对稳定性的影响。

图10　施加100 g轴向过载时弹体的根轨迹图Fig.10 Root loci of missile（a=100 g）

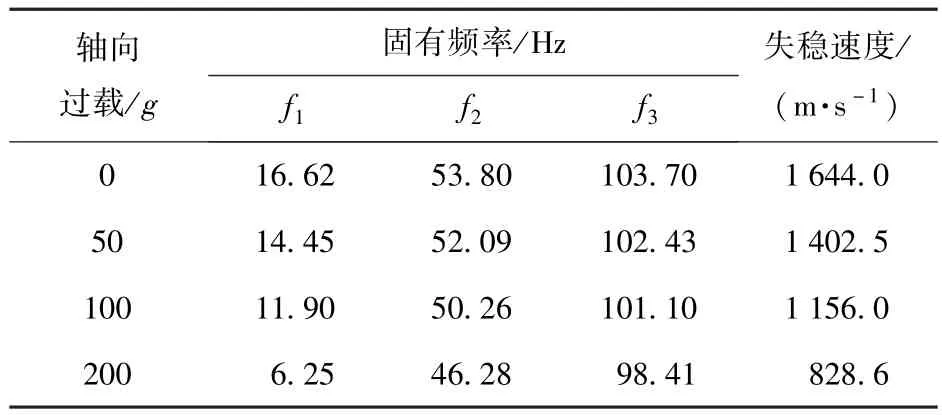
表2　弹体稳定性分析结果Tab.2 Analysis results of stability of slender missile under different axial loads

3　结论

本文采用有限元方法研究了轴向过载对大长细比导弹刚度特性的影响。采用当地流活塞理论和结构运动方程的耦合求解，综合考虑弹性模态和刚性模态，研究了轴向过载对大长细比导弹稳定性的影响，得到如下结论：

1）弹体施加轴向载荷时，其刚度特性会随着轴向载荷的增加而减小，其中1阶模态的变化比较明显。随着轴向载荷增大，1阶模态固有频率显著降低，振型也发生变化。

2）由于导弹的长细比较大，弹性效应强，结构的弹性变形会影响弹体的刚体模态稳定性，发生耦合失稳，故导弹的稳定性分析需要同时考虑弹性模态和刚性模态。

3）考虑轴向过载后，大长细比导弹的失稳速度随着轴向过载的增加而降低。对本文中算例，100 g过载时弹体的失稳速度已降低了约30%.轴向过载对大长细比导弹稳定性的影响不可忽略。

图11　施加100 g轴向过载时弹体不同速度下的时域响应曲线Fig.11 Time responses of generalized displacements at various velocities（a=100 g）

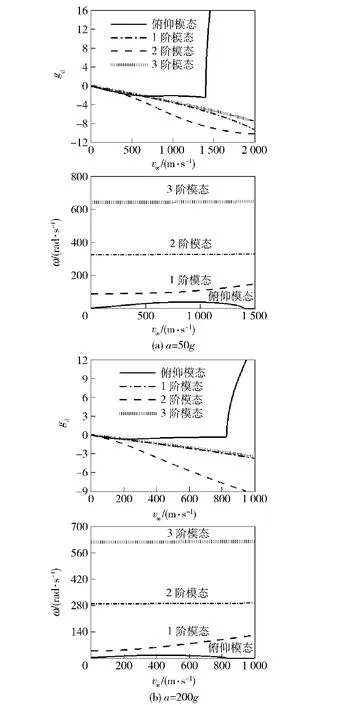
图12　弹体施加50 g、200 g轴向过载时的稳定性分析结果Fig.12 Analysis result of stability of slender missile（a=50 g，a=200 g）

（

）

［1］Beal T R.Dynamic stability of flexible missile under constant and pulsating thrust［J］.AIAA Journal，1965，3（3）：486-494.

［2］Ohshima T，Sugiyama Y.Dynamic stability of free-free beam subjected to end rocket thrust and carrying a heavy payload at its nose［C］∥2003 International Conference on Physics and Control.Saint Petersburg，Russia：IEEE，2003：1115-1120.

［3］Pourtakdoust S H，Assadian N.Investigation of thrust effect on the vibrational characteristics of flexible guided missiles［J］.Journal of Sound and Vibration，2004，272（1）：287-299.

［4］宋健.在推力和阻力作用下飞行器横向振动分析［J］.中国工程科学，2000，2（10）：63-72. SONG Jian.Lateral vibration analyses of flying vehicle under thrust and drag［J］.Engineering Science，2000，2（10）：63-72.（in Chinese）

［5］许赟，谢长川，杨超.推力作用下细长弹箭横向振动及稳定性分析［J］.工程力学，2009，26（12）：211-215. XU Yun，XIE Chang-chuan，YANG Chao.Transverse vibration and dynamic stability analysis of slender projects under thrust［J］.Engineering Mechanics，2009，26（12）：211-215.（in Chinese）

［6］王良明.细长弹箭气动弹性稳定性研究［J］.兵工学报，2001，22（1）：31-33. WANG Liang-ming.Aeroelastic stability conditions for large L/D ration rockets［J］.Acta Armamentarii，2001，22（1）：31-33.（in Chinese）

［7］吴小胜，黄晓鹏.大长细比导弹气动弹性数值计算研究［J］.北京理工大学学报，2010，30（4）：379-383. WU Xiao-sheng，HUANG Xiao-peng.Numerical study on the areoelasticity of a large fineness ratio projectile［J］.Transactions of Beijing Institute of Technology，2010，30（4）：379-383.（in Chinese）

［8］Wu Lei，Xie Chang-chuan，Yang Chao.Aeroelastic stability of a slender missile with constant thrust［J］.Procedia Engineering，2012，31：128-135.

［9］吴志刚，杨超.弹性导弹的连续与离散阵风响应［J］.北京航空航天大学学报，2007，33（2）：136-140. WU Zhi-gang，YANG Chao.Continuous and discrete gust responses of elastic missiles［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33（2）：136-140.（in Chinese）

［10］张雷，彭程，王永，等.大长径比导弹两自由度H∞减振跟踪控制器设计［J］.弹道学报，2010，22（4）：1-5. ZHANG Lei，PENG Cheng，WANG Yong，et al.Two-degree-offreedom H∞controller design for vibration attenuation and tracking of high length-to-diameter ratio missile［J］.Journal of Ballistics，2010，22（4）：1-5.（in Chinese）

［11］吴志刚，楚龙飞，杨超，等.推力耦合的高超声速飞行器气动伺服弹性研究［J］.航空学报，2012，33（8）：1355-1363. WU Zhi-gang，CHU Long-fei，YANG Chao，et al.Study on aeroservoelasticity of hypersonic vehicles with thrust coupling［J］.Acta Aeronautica et Astronautica Sinica，2012，33（8）：1355-1363.（in Chinese）

［12］陈劲松，曹军.超声速和高超声速翼型非定常气动力的一种近似计算方法［J］.空气动力学学报，1990，8（3）：339-343. CHEN Jing-song，CAO Jun.An approximate calculating method of supersonic/hypersonic unsteady aerodynamic forces of airfoils［J］. Acta Aerodynamica Sinica，1990，8（3）：339-343.（in Chinese）

［13］杨炳渊，宋伟力.用当地流活塞理论计算大攻角翼面超音速颤振［J］.振动与冲击，1995，14（2）：60-63. YANG Bing-yuan，SONG Wei-li.Supersonic flutter calculation of a wing with attack angle by local flow piston theory［J］.Journal of Vibration and Shock，1995，14（2）：60-63.（in Chinese）

［14］Zhang Wei-wei，Ye Zheng-yin，Zhang Chen-an.Supersonic flutter analysis based on a local piston theory［J］.AIAA Journal，2009，47（10）：2321-2328.

［15］张陈安，张伟伟，叶正寅.基于当地流活塞理论的气动弹性稳定性分析方法研究［J］.工程力学，2007，24（2）：22-27. ZHANG Chen-an，ZHANG Wei-wei，YE Zheng-yin.Aeroelastic analysis methods based on local piston theory［J］.Engineering Mechanics，2007，24（2）：22-27.（in Chinese）

［16］张陈安，张伟伟，叶正寅.一种基于当地流活塞理论的超音速导弹气动伺服弹性分析方法［J］.宇航学报，2007，28（1）：141-146. ZHANG Chen-an，ZHANG Wei-wei，YE Zheng-yin.An aeroservoelastic analysis method for supersonic missiles based on local piston theory［J］.Journal of Astronautics，2007，28（1）：141-146.（in Chinese）

Analysis on Stability of a Slender Missile under Axial Loads

QUAN Jing-ge，YE Zheng-yin，ZHANG Wei-wei
（National Key Laboratory of Aerodynamic Design and Research，Northwestern Polytechnical University，Xi'an 710072，Shaanxi，China）

For slender missile，there is a potential coupling effect between rigid mode and elastic mode，which makes the system unstable.As the axial loads have a negative effect on the structural stiffness property，the stability of the system gets worse further.A finite element method is used to study the influence of the axial loads on the structural stiffness property of missile.The local piston theory coupled with the structural motion equations is developed to analyze the stability of a slender missile in state-space.It is shown that the rigid mode and elastic mode of the slender missile couple together under high axial loads，resulting in the system instability.Moreover，as the axial acceleration loads increase，the structural stiffness of the missile reduces，and the critical instable speed falls.

ordnance science and technology；high slenderness ratio；missile；local piston theory；axial load；coupling instability

TJ760.1；V415.3

A

1000-1093（2015）01-0094-09

10.3969/j.issn.1000-1093.2015.01.014

2014-03-03

教育部新世纪优秀人才支持计划项目（NCET-13-0478）

全景阁（1985—），女，博士研究生。E-mail：pigeon729@163.com；叶正寅（1963—），男，教授，博士生导师。E-mail：yezy@nwpu.edu.cn