互耦效应下一种基于实值稀疏表示的波达方向估计算法

吴振，戴继生，2，朱湘临，赵德安

（1.江苏大学电气信息工程学院，江苏镇江212013；2.东南大学移动通信国家重点实验室，江苏南京210096）

互耦效应下一种基于实值稀疏表示的波达方向估计算法

吴振1，戴继生1，2，朱湘临1，赵德安1

（1.江苏大学电气信息工程学院，江苏镇江212013；2.东南大学移动通信国家重点实验室，江苏南京210096）

针对未知互耦条件下的波达方向（DOA）估计问题，提出了一种未知互耦条件下基于实值稀疏表示的加权子空间DOA估计算法。新算法利用一个特定的酉变换矩阵，将一个复杂的复值优化问题转化为一个实值优化问题，从而有效地将原问题的计算复杂度减少4倍以上。此外，为了进一步提高稀疏表示的估计算法估计精度，在原有l1范数优化模型基础上引入一个能使得DOA估计方差取得最小值的最优子空间加权矩阵。仿真实验表明，在低信噪比情况下，新算法能进一步提高稀疏表示的估计算法抗噪能力，获得更好的估计精度。

信息处理技术；波达方向估计；稀疏表示；互耦；均匀线阵

0　引言

波达方向（DOA）估计作为阵列信号处理的一个重要分支，已广泛应用于雷达、声纳、通信、地震勘探、射电天文以及生物医学工程等多个领域［1-3］。基于子空间的DOA估计算法（MUSIC、ESPRIT、root-MUSIC，WSF等）在较高信噪比、较多快拍数的条件下具有较好的估计性能，但在非理想（比如低信噪比、少量快拍数）情况下，此类算法性能将损失严重。稀疏表示作为一种新颖的数据处理方法，近年来得到了国内外学者的极大关注。基于稀疏表示的DOA估计算法与其他估计算法相比，具有所需快拍数小、在低信噪比下具有良好的抗噪性、适用相干信号等优点［4-5］。

稀疏表示估计算法也存在一些不足：与大多数子空间估计算法一样，其估计性能很大程度上取决于阵列流型是否精确已知。在实际的工程应用中，不可避免地要面临多种流型误差的影响（如阵元幅相误差、阵元位置误差、阵元间互耦效应等），这些误差将使得未经校准处理的DOA估计算法的性能严重恶化，甚至失效［6-10］。为对抗阵元间的互耦效应，Dai等提出了一种未知互耦条件下的稀疏表示的DOA估计算法［6］。该算法能够消除未知互耦因素带来的不利影响，提高DOA估计的性能。然而该算法需要求解一个复数域上的关于l1范数的优化问题，其计算复杂量较高。

注意到一次复数乘法运算需要4次实数乘法运算和两次实数加法运算，因此，复数实值化将带来计算复杂度上的巨大优势。受此启发，本文拟提出一种未知互耦条件下基于实值稀疏表示的加权子空间（WSF）DOA估计算法。与文献［6］所提算法相对比，新算法的创新之处在于：1）采用了实值变换矩阵，有效地将计算复杂度减少4倍以上；2）在目标函数中引入了一个最优子空间加权矩阵，有助于进一步减小DOA估计的方差。因此，新算法是文献［6］所提算法的一个重要推广，其既有助于提高DOA估计性能，又能有效地降低算法计算复杂度。

1　信号模型

考虑K个波达方向为θ1，θ2，…，θK的窄带互不相关信号sk（t）（k=1，2，…，K）从远场入射到由M个阵元组成的均匀线阵（ULA）上，其中信号波长为λ.若假设相邻阵元间距为d，则未知互耦条件下阵列的输出信号r（t）为

式中：r（t）=［r1（t），r2（t），…，rM（t）］T；s（t）=［s1（t），s2（t），…，sK（t）］T；n（t）=［n1（t），n2（t），…，nM（t）］T；A=［α（θ1），α（θ2），…，α（θK）］；α（θk）=［1，ejφ（θk），…，ej（M-1）φ（θk）］T，φ（θk）=（-2πd/λ）·sin（θk）.n（t）是一个零均值方差为的广义高斯随机过程。矩阵C为ULA所对应的互耦矩阵，其互耦系数与阵元间距呈反比：足够远的两阵元间互耦系数近似为0，且间距相同的两阵元间互耦系数相同。因此，ULA的互耦矩阵可以用一个带状的对称Toepliz矩阵来描述。若模型只考虑m个阵元之间的相互作用，则互耦矩阵C［7-12］可表示为

式中：Toepliz（c）表示由矢量c构成的对称Toepliz矩阵，c为2M-1维矢量，且有

2　稀疏表示的DOA估计算法简介

为了便于分析，简要介绍一下无互耦效应下的稀疏表示的DOA估计算法（详见文献［4］）。此时，（1）式为

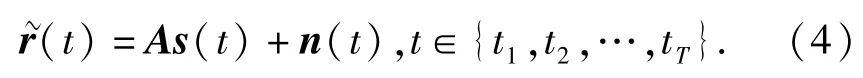
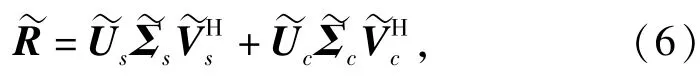
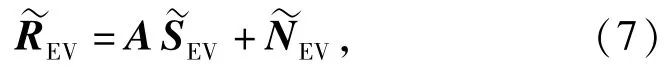
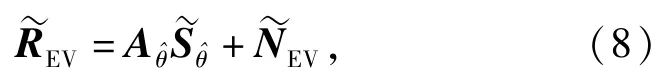
3　未知互耦条件下实值稀疏表示的DOA估计算法

由第2节叙述可知，文献［4］所提算法没有考虑互耦效应带来的不利影响。本节将提出一种未知互耦条件下基于实值稀疏表示的加权子空间DOA估计算法。与（5）式类似，未知互耦条件下，（1）式可表示为

由于C为未知矩阵，所以（10）式不能直接转换成稀疏表示的形式。为了去除互耦对阵列输出信号带来的不利影响，并将（10）式实值化，引入一个常数矩阵F≜［0（M-2m）×mIM-2m0（M-2m）×m］和一个酉变换矩阵QM：当M为偶数时，

当M为奇数时，

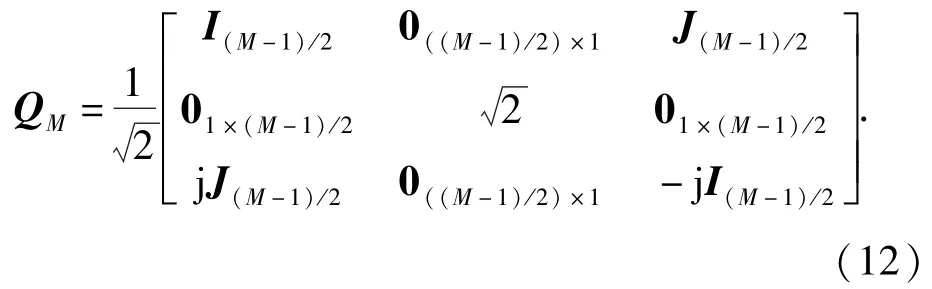
式中：I为单位矩阵；J为交换矩阵（反对角线元素全为1，其他元素为0的矩阵），下标表示矩阵维数。（10）式两边同时左乘F和QM-2m，得［12］

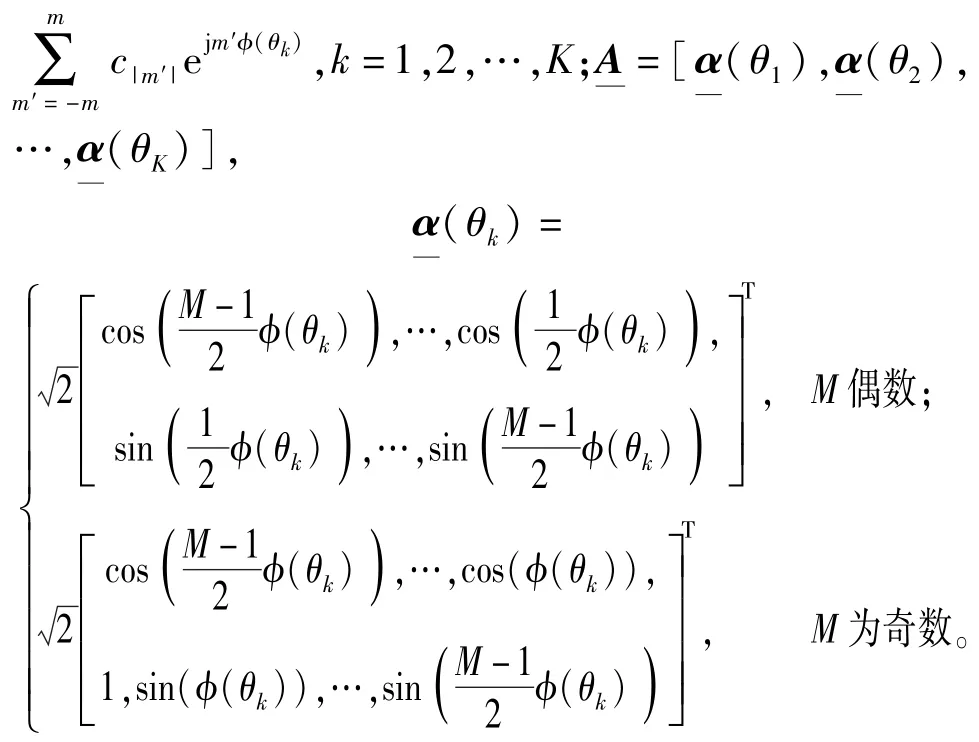
（13）式中QM-2mFR，和QM-2mFN同为复矩阵。为了进一步对其实值化，将（13）式改写成实部和虚部之和的形式，即

根据实部和虚部分别相等的必要条件，有

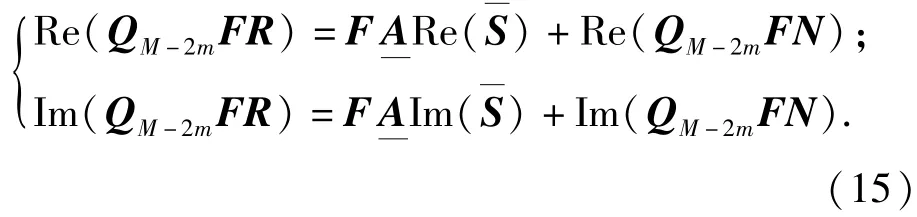
若将（15）式写成矩阵形式，得

根据（7）式，可类似地处理（16）式，但为了在低信噪比情况下，进一步提高稀疏表示的估计算法抗噪能力，获得更好的估计精度，不再简单地用同时右乘（16）式的两边，而是根据加权子空间理论，采用一个子空间实值加权矩阵W：

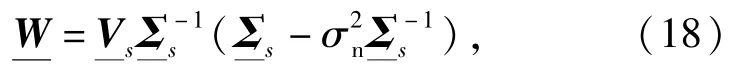
由文献［13］的定理3可知：对于任意的加权矩阵W，有

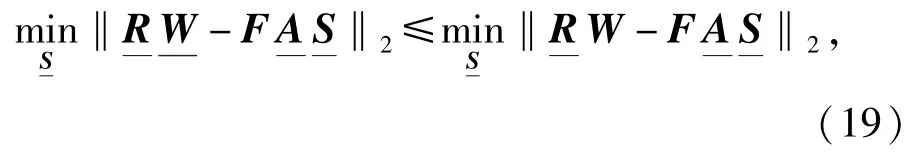
本文所提算法所涉及的l1范数优化问题（23）式与文献［6］的优化问题具有相同的结构，主要区别在于：1）优化问题（23）式中所有已知变量和需优化的变量均为实值；2）引入了一个子空间实值加权矩阵，使得DOA估计的方差能取得最小值。由于一次复数乘法运算需要4次实数乘法运算和两次实数加法运算，因此，复变量实值化将带来计算复杂度上的巨大优势：直接求解优化问题（23）式所需的计算复杂度仅为求解文献［6］优化问题计算复杂度的1/4.详细的讨论可参见文献［12，14-15］，这里不在赘述。

4　仿真结果及实验分析

本节中将新算法与文献［6，8］所提的算法进行比较，从而验证新算法的有效性。在第1个仿真实验中，假设K=2个不相关信号（θ1=-19.7°，θ2= 10.1°）入射到阵元数为M=10的ULA上，阵元间距为半波长，仅考虑相邻阵元间存在互耦效应，且互耦系数为0.384 4-0.347 6i，噪声为零均值的高斯白噪声。每次实验均进行200次蒙特卡罗实验，采用均方根误差（RMSE）作为DOA估计算法性能的衡量指标，其定义为

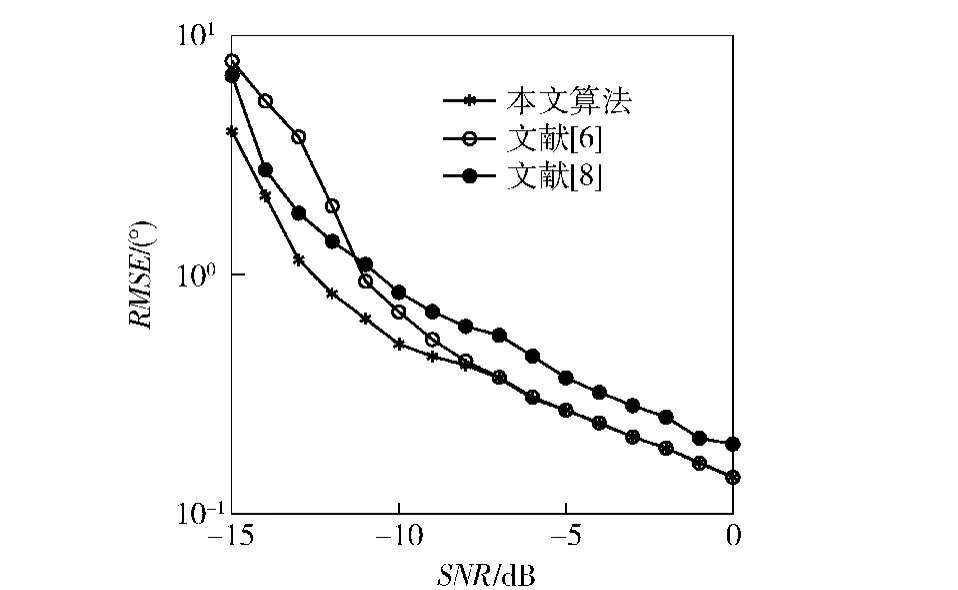
图1　不同DOA估计算法的RMSE随着SNR变化的性能曲线Fig.1 RMSE of DOA estimate against SNR among different strategies

为了验证快拍数对算法性能产生的影响，在第2个仿真实验中，在低信噪比情况下进行了RMSE随快拍数变化的仿真实验。除了将SNR设置为一个固定值（-10 dB），其他实验条件与仿真实验1相同。图2描述了不同DOA估计算法的RMSE随着快拍数变化的性能曲线。从图2可以看出，本文算法性能明显优于其他算法，而且随着快拍数的增加，所提算法的DOA估计RMSE逐渐减小，即估计精度逐渐增高。

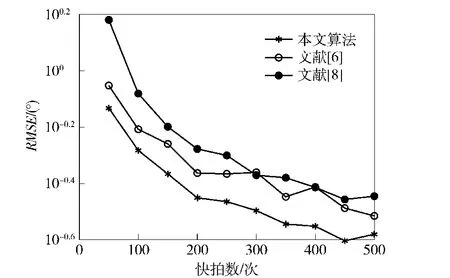
图2　不同DOA估计算法的RMSE随着快拍数变化的性能曲线Fig.2 RMSE of DOA estimate against snapshots among different strategies

在第3个仿真实验中，将验证较少快拍数情况下算法的角度辨别性能。设为第k个信号的角度估计值，若，则称算法能分辨出相邻的DOA.该仿真实验假设有两个相邻的不相关信号（θ1=-2.5°，θ2=3.5°）入射到阵元数为M=12的均匀线阵上，阵元间距为半波长，快拍数为50，阵元间互耦系数设为c=［1，0.4+0.3i，0.1-0.2i］.图3描述了不同DOA估计算法的分辨率随着SNR变化的性能曲线。由图3可以看出，本文所提算法具有较高的角度分辨率。

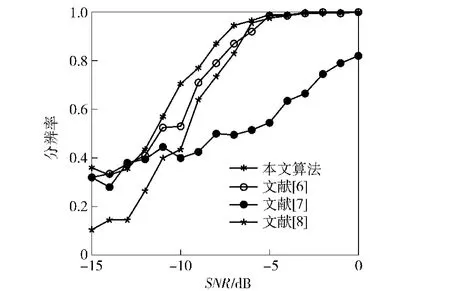
图3　不同DOA估计算法的分辨率随着SNR变化的性能曲线Fig.3 Resolution probability of DOA estimate against SNR among different strategies

5　结论

针对未知互耦条件下DOA估计算法运算复杂度较高的问题，本文提出一种未知互耦条件下基于实值稀疏表示的加权子空间DOA估计算法，该算法利用特定的酉变换矩阵，将一个复杂的复值优化问题转化成实值优化问题，从而有效地降低了计算复杂度。此外，根据加权子空间理论，引入了一个子空间实值加权矩阵，进一步提高了稀疏表示的估计算法估计精度。本文算法是文献［6］所提算法的一个重要推广。理论分析和仿真实验都验证了本文所提算法的有效性。

（

）

［1］Kim H，Viberg M.Two decades of array signal processing research［J］. IEEE Signal Magazine，1996，13（4）：67-94.

［2］叶中付，李春辉，贾红江，等.空间非平稳噪声下的信源数估计算法［J］.兵工学报，2009，30（7）：873-878. YE Zhong-fu，LI Chun-hui，JIA Hong-jiang，et al.Estimation of the number of signal source in spatially nonstationary noise［J］. Acta Armamentarii，2009，30（7）：873-878.（in Chinese）

［3］邹吉武，孙大军.线阵双基地声纳波束零点形成MUSIC算法［J］.兵工学报，2010，31（3）：364-368. ZOU Ji-wu，SUN Da-jun.MUSIC algorithm of beam null forming on linear array of bi-static sonar［J］.Acta Armamentarii，2010，31（3）：364-368.（in Chinese）

［4］Malioutov D，Çetin M，Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays［J］. IEEE Transactions on Signal Processing，2005，53（8）：3010-3022.

［5］Stoica P，Babu P，Li J.SPICE：a sparse covariance-based estimation method for array processing［J］.IEEE Transactions on Signal Processing，2011，59（2）：629-638.

［6］Dai J，Zhao D，Ji X.A sparse representation method for DOA estimation with unknown mutual coupling［J］.IEEE Antennas and Wireless Propagation Letters，2012，11：1210-1213.

［7］Sellone F，Serra A.A novel online mutual coupling compensation algorithm for uniform and linear arrays［J］.IEEE Transactions on Signal Processing，2007，55（2）：560-573.

［8］Ye Z，Dai J，Xu X，et al.DOA estimation for uniform linear array with mutual coupling［J］.IEEE Transactions on Aerospace and E-lectronic Systems，2009，45（1）：280-288.

［9］Friedlander B，Weiss A J.Direction finding in the presence of mutual coupling［J］.IEEE Transactions on Antennas and Propagation，1991，39（3）：273-284.

［10］Dai J，Bao X，Hu N，et al.A recursive RARE algorithm for DOA estimation with unknown mutual coupling［J］.IEEE Antennas and Wireless Propagation Letters，2014，13：1593-1596..

［11］Dai J，Ye Z.Spatial smoothing for direction of arrival estimation of coherent signals in the presence of unknown mutual coupling［J］. IET Signal Processing，2011，5（4）：418-425.

［12］Dai J，Xu W，Zhao D.Real-valued DOA estimation for uniform linear array with unknown mutual coupling［J］.Signal Processing，2012，92（9）：2056-2065.

［13］Viberg M，Ottersten B.Sensor array processing based on subspace fitting［J］.IEEE Transactions on Signal Processing，1991，39（5）：1110-1121.

［14］Huarng K C，Yeh C C.A unitary transformation method for angle-of-arrival estimation［J］.IEEE Transactions on Signal Processing，1991，39（4）：975-977.

［15］Dai J，Xu X，Zhao D.Direction-of-arrival estimation via realvalued sparse representation［J］.IEEE Antennas and Wireless Propagation Letters，2013，12：376-379.

A Real-valued Sparse Representation Method for DOA Estimation with Unknown Mutual Coupling

WU Zhen1，DAI Ji-sheng1，2，ZHU Xiang-lin1，ZHAO De-an1
（1.School of Electrical and Information Engineering，Jiangsu University，Zhenjiang 212013，Jiangsu，China；2.National Mobile Communications Research Laboratory，Southeast University，Nanjing 210096，Jiangsu，China）

The paper presents a real-valued sparse representation method for DOA estimation in the presence of unknown mutual coupling.Utilizing a certain unitary transformation and taking advantage of the special structure of mutual coupling matrix（MCM）for uniform linear arrays（ULAs），we are able to convert complex-valued manifold matrices of ULAs with unknown mutual coupling into real ones.Due to this transformation，the computational complexity can be decreased by a factor of at least four.Moreover，the proposed method is expected to have a better noise suppression，as it exploits an additional optimal weighting matrix.Thus，the proposed method outperforms the original one，especially when signal-tonoise ratio（SNR）is low.Simulation results verify the efficiency of the proposed method.

information processing technology；direction of arrival estimation；sparse representation；mutual coupling；uniform linear array

TN911.7

A

1000-1093（2015）02-0294-05

10.3969/j.issn.1000-1093.2015.02.015

2013-09-27

国家自然科学基金项目（61102054）；东南大学移动通信国家重点实验室开放研究基金项目（2013D08）

吴振（1990—），男，硕士研究生。E-mail：zhenwu.ujs@gmail.com；戴继生（1982—），男，副教授，硕士生导师。E-mail：jsdai@ujs.edu.cn