基于Matlab Simulink的弹道仿真方法

黄　成，于　鹏，赵锡旺（. 9550部队，辽宁大连60；.海军装备部，北京0008；. 970部队，山东威海6409）



基于Matlab Simulink的弹道仿真方法

黄成1，于鹏2，赵锡旺3
（1. 91550部队，辽宁大连116023；2.海军装备部，北京100083；2. 92270部队，山东威海264309）

摘要：弹道仿真软件有助于飞航导弹武器飞行试验结果的分析与评定。为此，设计了基于Matlab Simulink 的弹道仿真计算方法，建立了六自由度空间弹道数学模型，利用导弹相关的气动数据和控制参数测试了算法，实现了软件，仿真结果证明了该模型的准确性和可信度。

关键词：弹道仿真；数学模型；仿真方法

飞行试验是导弹研制定型过程中的一个关键环节。从以往的导弹飞行试验来看，当导弹在飞行试验中出现故障或问题时，试验现场常因欠缺弹道仿真软件而陷入被动，这在一定程度上影响了试验进展。近年来，国内关于导弹的仿真，大多集中于仿真训练和仿真视景的研究[1-5]，而对于辅助导弹飞行试验结果分析、评定的仿真研究相对较少。为加强对飞航导弹武器系统飞行试验结果的分析与评定，亟需深入开展便利、有效的相关弹道仿真方法研究。

对飞航导弹的全弹道仿真来讲，仿真研究的全过程涉及到多个功能模块的设计难题，如参数装定模块、运算模块、结果处理模块、运行控制模块等，各仿真模块间存在着密切关联。运用Matlab Simulink建模工具，采用模块化程序设计，允许用户根据任务的需要，建立多种子模型，各子模型间采用模块拼装方式，允许自由组合，通过界面交互问答确定仿真模型、算法及输出形式。力求在模型的组合、算法的选择及气动力数据的插值方面提供灵活便利的操作方式[6]。

1　仿真模型的建立

1.1坐标系变换关系

坐标系包括：指北地理坐标系、弹体坐标系、速度坐标系、游移方位坐标、弹道坐标系和风速坐标系，相互之间通过欧拉角方程转换。坐标系定义和各个坐标系之间转换关系详见文献[7]。

ip,、为弹体绕惯性坐标系的转动角速度在弹体轴上的3个投影；M、M、Mz为气动力矩的分量；Mp、Mp、Mzp为发动机推力偏心产生的力矩分量；ΔM、ΔM、ΔMz为外界干扰力矩的分量；ψ、ϑ、γ为偏航角、俯仰角、滚动角；为导弹弹体相对于平台坐标系的姿态速率。

1.3子模型的建立

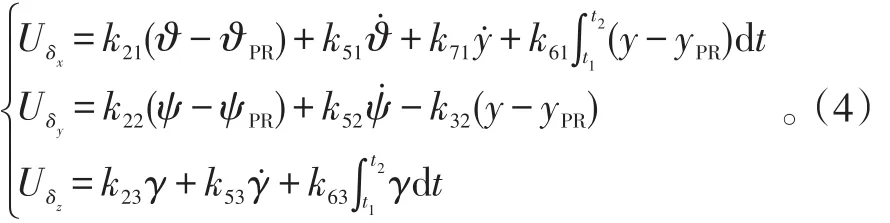
1）控制系统模型。控制系统通常采用的方案为PID调节规律：式（4）中：Uδ、Uδ、Uδz为舵机的输入电压值；ψPR、ϑPR为程序偏航角、程序俯仰角；、PR为巡航高度、程序高度；kij为控制参数集。

2）指令装订模型。指令装订模型是指用户根据仿真任务的需要预先装入的飞行方案，飞行方案参数由用户确定。

3）地形匹配模型。根据仿真任务要求，需要采用地形匹配技术，匹配模型根据实际匹配计算参数修改指令装订参数。

4）舵机回路模型。舵机采取何种反馈信号由具体情况而定。舵信号经舵回路应给出控制导弹运动的舵偏角信号。

5）质量/惯量模型。数字仿真用到的导弹总体参数主要包括：导弹质量m，绕重心的转动惯量J、J、Jz，质心位置cm、cm、Zcm。在满油（药）、空油（药）状态下，总体参数见表1。

表1　导弹总体参数表Tab.1 Parameter table of missile overall

在飞行中要确定重心位置和转动惯量的变化规律，依线性变化可以得出：

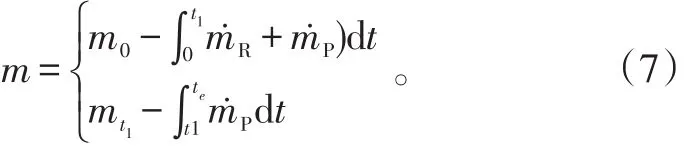
质量变化由一、二级装药（燃油）秒消耗量决定：式（7）中：t1为助推器脱离时间；te为飞行终止时间；m0为起飞质量；mt1为抛掉助推器后的质量；R为固体装药秒消耗量；P为燃油秒消耗量。

6）气动力模型。导弹在飞行中所受的气动力有升力、阻力与侧向力，作用在导弹上的气动力矩为俯仰力矩Mz、偏航力矩M及滚转力矩M。同时，仿真计算中要计算铰链力矩Mh,、Mh,、Mh,z。

在导弹气动力计算中，首先要明确参考长度L，参考面积S。

阻力系数C、侧向力系数C、升力系数Cz和转动力矩系数m主要由以下几个方面构成：导弹飞行中还包括动导数铰链力矩系数为：

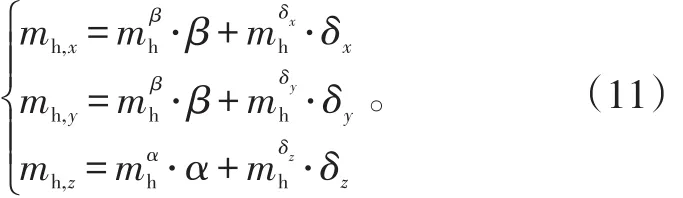
7）发动机模型。飞航式导弹一般采用涡喷（扇）发动机，发动机推力特性及燃油秒消耗量与飞行马赫数Ma、高度h、发动机转速n、大气温度T、总压恢复系数ρ0等参数有关：

若发动机推力数据以离散数据形式给出，可以采用五维插值得到。

8）指数型大气模型。采用指数型大气密度变化模型，大气密度为

若ρ0取海平面的大气密度，则h0=0；H-为大气标量高度。

9）地球模型。将地球当作一个旋成圆球体，圆球半径为常数（RE=6371.221km），即假定在地球表面不同经纬度的曲率半径相同；地球自转角速度；引力加速度；μ=3 .986×1014m3/s2表示引力常数与地球质量之积，g0=9.81 m/s2表示海拔高度为0时的重力加速度，方向指向地心。

10）阵风模型。阵风模型采用“1 - cos”模型，阵风速度的3个分量均可以用下面的模型描述，以垂直风速为例：

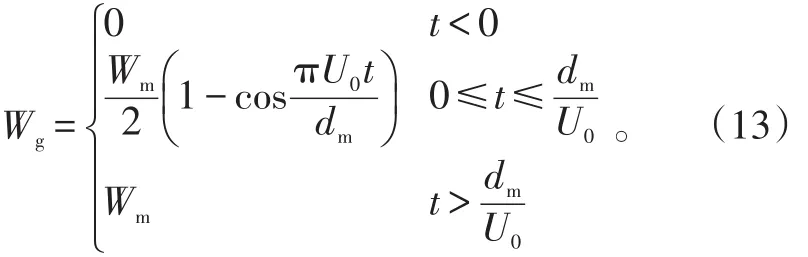
m对象的各固有频率。

11）海浪模型。采用典型一维PM海浪谱作为海浪模型[8]。

2　基于Matlab的程序设计

随着计算机技术的快速发展，利用各种高级语言基本上都可以开发出导弹飞行仿真平台，但较为合适的语言应该是Matlab、C或者Fortran等计算功能强大的语言。

本文采用的是Matlab提供的动态系统仿真工具Simulink，它是众多仿真软件中功能最强大、最优秀、最容易使用的一种[9]。在Simulink中，对系统建模将变得简单，而且仿真过程是交互的。因此，可以很随意地改变仿真参数，并且立即可以得到修改后的仿真结果。另外，使用Matlab中的各种分析工具，还可以对仿真结果进行分析和可视化。导弹空间弹道数学模型结构框图如图1所示，基于Simulink的雷达模型如图2所示。

图1　导弹空间弹道数学模型结构框图Fig.1 Structure diagram of missile ballistic math model

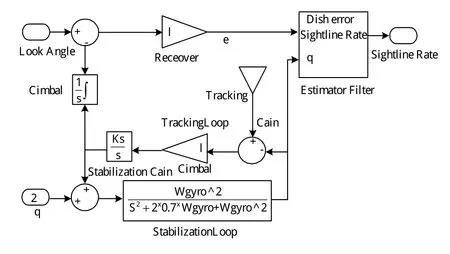
图2　基于Simulink的雷达模型Fig.2 Radar model based on the Simulink

3　模型校验及仿真结果

3.1模型校验

采用频谱分析法对全系统模型直接进行模型验证，即将相同初始条件下全系统仿真模型的运行结果与真实弹道数据进行比较，从而反应出模型的准确性和可信度[10-11]。对海浪和大气紊流等扰动模型的校验即对仿真得到的数据进行谱估计，将得到的估计谱与理论谱进行拟合，根据拟合结果来判断仿真模型与理论模型的近似程度，见图3、4。

图3　弹-浪夹角为0时谱拟合情况Fig.3 Situation of spectral fitting when the angle between missile and waves to 0

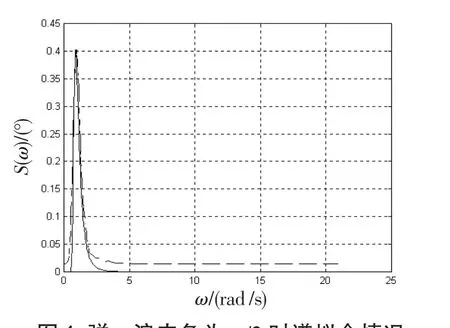
图4　弹-浪夹角为π/2时谱拟合情况Fig.4 Situation of spectral fitting when the angle between missile and waves to π/2

3.2仿真计算

利用文中算法，对某飞航式导弹进行了多条弹道的仿真计算，并结合历次的靶场试验进行分析和研究，验证了算法；同时也对模型进行了有效性验证[12]。图5是相同初始条件下，导弹仿真结果与实际飞行弹道对照曲线。

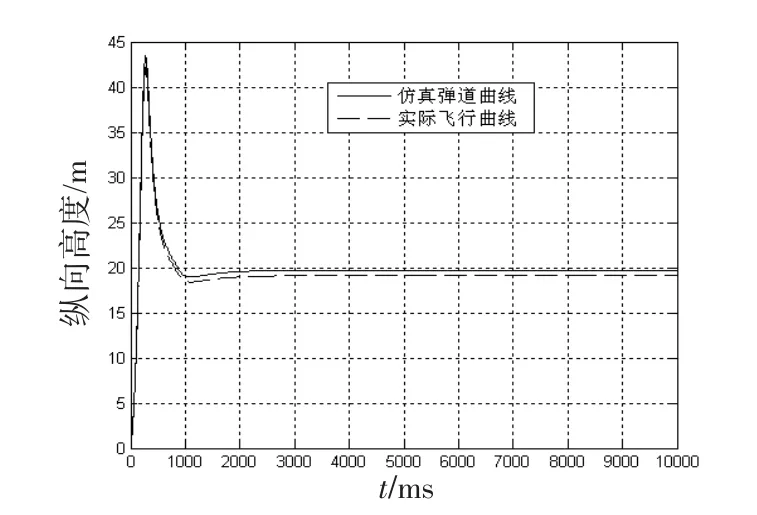
图5　仿真结果与实际飞行弹道对照曲线Fig.5 Contrast curve between simulation result and actual flight trajector

3.3仿真结论

通过多次的仿真计算，得出下述结论：

1）采用模块化的弹道仿真模型建立方法，按面向应用及面向对象思想设计可以实现软件；

?

2）频谱分析法在系统仿真模型校验过程中得到了成功应用，结合靶场试验数据可以进行算法验证和模型有效性验证；

3）利用Matlab Simulink进行系统仿真，可以满足试验分析的需求，而且在系统模型建立、程序设计、模型验证、仿真试验和数据分析处理等方面都提供了极大的便利。

4　结束语

对于飞航式导弹全弹道仿真来讲，研究过程中要优化各个功能模块，提高仿真效率和仿真软件的可用性，注重仿真环境的一体化，这样可以对仿真资源进行统一的管理。

在本方法的数学公式组织过程中，既参考了经典的数字仿真理论和已有的成功经验，也采用了近几年来的一些新技术及新标准。模型设计务求方法详尽、条理清楚。本仿真方法具有通用性，更新相关模块就可对新型号飞航式导弹进行弹道仿真计算。

参考文献：

[1]李小龙.地地战术导弹测试发控系统训练仿真器研究[D].哈尔滨：哈尔滨工业大学，2002. LIIAOLONG. Research of training simulator in tactical missile test control sstem[D]. Harbin：Harbin Institute of Technolog，2002.（in Chinese）

[2]郭会明，杨明，李雷，等.地空导弹训练仿真系统的设计与实现[J].系统仿真学报，2003，26（1）：69-87. GUO HUIMING，ANG MING，LI LEI，et al. Design and implementation of the training simulator for the surface- to- air missile[J]. Journal of Sstem Simulation，2003，26（1）：69-87.（in Chinese）

[3]郭希维，苏群星，谷宏强.导弹训练仿真系统中信号的采集与处理[J].兵工自动化，2004，23（2）：4-6. GUOIWEI，SU QUNIN，GU HONGQIANG. Signal acquisition and processing in training simulation sstem for missile[J]. Ordance IndustrAutomation，2004，23 （2）：4-6.（in Chinese）

[4]向哲，李善高，邱发廷，等.反舰导弹靶场试验视景仿真技术[J].海军航空工程学院学报，2010，25（2）：235-237.IANG ZHE，LI SHANGAO，QIU FATING，et al. Scene simulation technologof certain anti- ship missile in range test[J]. Journal of Naval Aeronautical and Astronautical Universit，2010，25（2）：235-237.（in Chinese）

[5]彭国圣，苏洪潮，李续武.基于Vega的某地空导弹视景技术研究[J].战术导弹技术，2003（5）：63-67. PENG GUOSHENG，SU HONGCHAO，LIUWU. Research on scene technologof certain air-to-ground missile based on vega[J]. Tactical Missile Technolog，2003 （5）：63-67.（in Chinese）

[6]张平. Matlab基础与应用简明教程[M].北京：航空航天大学出版社，2001：156-158. ZHANG PING. Matlab foundation and application of introductortutorial[M]. Beijing：Beihang UniversitPress，2001：156-158.（in Chinese）

[7]李宗吉，程善政，刘洋.蒙特卡洛模拟法计算航空自导深弹命中概率[J].弹箭与制导学报，2012，32（2）：22-24. LI ZONGJI，CHENG SHANZHEN，LIUANG. The calculation of aerial homing-depth charge hitting probabilitbmonte-carlo method[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2012，32（2）：22-24.（in Chinese）

[8]顾文锦，叶显武.导弹仿真中海浪的数字仿真及其动画生成[J].系统仿真学报，1998，10（1）：33-38. GU WENJIN，EIANWU. Digital simulation and animation generation of sea-wave in the simulation of thesubmarine-launched missile[J]. Journal of Sstem Simulation，1998，10（1）：33-38.（in Chinese）

[9]刘云南.基于Matlab和Simulink的导弹弹道仿真与应用[J].弹箭与制导学报，2011，31（3）：183-185. LIUUNNAN. Model building and application of missile simulation based on matlab and simulink[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2011，31 （3）：183-185.（in Chinese）

[10]周广东.基于小波变换的非平稳脉动风时变功率谱估计方法研究[J].工程力学，2013，30（3）：89-97. ZHOU GUANGDONG. Estimation method of evolutionarpower spectrum for non-stationarfluctuating wind using wavelet transforms[J]. Engineering Mechanics， 2013，30（3）：89-97.（in Chinese）

[11]廖瑛.系统建模与仿真的校核、验证与确认（VV&A）技术[M].长沙：国防科技大学出版社，2006：110-116. LIAOING. Technologabout verification validation and accreditation of the modeling and simulation[M]. Changsha：National Universitof Defense TechnologPress，2006：110-116.（in Chinese）

[12]吴海霞.蒙特卡罗方法在实际问题中的应用[J].太原师范学院学报，2009，8（1）：76-79. WU HAIIA. Monte carlo method and applications in solving special problems[J]. Journal of Taiuan Normal Universit，2009，8（1）：76-79.（in Chinese）

HUANG Cheng1,U Peng2, ZHAOi-wang3
（1. The 91550thUnit of PLA, Dalian Liaoning 116023, China; 2. Naval Equipment Department, Beijing 100083, China; 3. The 92270thUnit of PLA, Weihai Shandong 264309, China）

Abstrraacctt:: The trajectorsimulation software can help to analze and evaluate the flight eperimental results of the winged missile weapon sstem. The trajectorsimulation method was designed based on Matlab Simulink, the mathematical model of missile trajectorwith sidegrees of freedom was established, and the software was programmed and tested using the aerodnamic data and control parameters of the missile. The simulation results is proved the model's accuracand reliabil⁃it.

作者简介：黄成（1978-），男，工程师，大学。

收稿日期：2014-08-16；

DOI:10.7682/j.issn.1673-1522.2015.02.016

文章编号：1673-1522（2015）02-0169-05

文献标志码：A

中图分类号：TP391.9

修回日期：2014-12-28