基于灰色模型的MEMS陀螺温度补偿
李 翊,刘 炜,吴凌华(.海军装备部驻西安地区军事代表局,西安70054;. 9980部队,山东烟台64000;.海军装备部驻成都地区军事代表局,成都6000)
基于灰色模型的MEMS陀螺温度补偿
李翊1,刘炜2,吴凌华3
(1.海军装备部驻西安地区军事代表局,西安710054;2. 91980部队,山东烟台264000;3.海军装备部驻成都地区军事代表局,成都610100)
摘要:首先,分析了温度对零偏的影响机理,并针对环境温度影响导致MEMS陀螺零位输出变化较大的问题,提出了一种基于灰色模型的温度补偿方法,即原始数据先通过灰色模型进行预处理;然后,根据灰色模型处理过的数据,建立一种补偿模型,并用该模型对测试的数据进行预测补偿。试验表明,采用该方法使陀螺零位在全温范围内稳定精度提高了一个数量级,证明了提出方法的可行性和有效性。
关键词:MEMS陀螺;机理分析;灰色模型;温度补偿
近年来,MEMS陀螺得到了很大的发展,并取得了一定的军事价值和社会经济效益。MEMS陀螺具有体积小、重量轻、价格低、易集成等优点,在航空航天、地质勘探、汽车工业及机器人领域具有广泛的应用价值及前景。
由于MEMS陀螺在精度和稳定度上都容易受自身材料、制造工艺以及工作环境各因素的影响,且随着功耗及外界温度的变化,MEMS陀螺的各项指标,如零偏、刻度因子、灵敏度等都会发生相应改变,其中,零偏是影响陀螺仪输出精度的主要因素[1]。在对陀螺仪精度要求较高的领域,它与实际应用有很大差距。这就要求人们采用各种可行的方法提高其精度。
1 温度对零偏影响的机理分析
MEMS陀螺是由单晶硅片采用光刻和各项异性刻蚀工艺制造而成的,是属于硅的微机械加工与陀螺仪理论相结合的产物。MEMS陀螺在温度发生变化时,其机械结构主要发生2种变化:尺寸的大小改变和材料弹性模量的改变,其中,尺寸随温度的改变对陀螺性能影响很小[2]。
MEMS陀螺性能受环境温度影响较大,陀螺材料的弹性模量及陀螺检测电路中电子器件的性能都会随温度的改变而变化,弹性模量的变化会导致系统刚度的变化,从而改变陀螺谐振频率,使其产生漂移[3-4]。
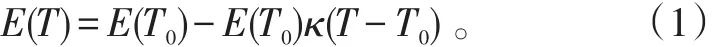
弹性模量与温度的变化关系可表示为式(1)中:E(T)、E(T0)分别是硅材料在温度为T、T0时的弹性模量,T0=300K;κ为硅材料弹性模量温度变化系数,其值约为5×10-7。

弹性系数与弹性模量的关系为式中,K、K0分别是温度为T、T0时系统弹性系数。陀螺谐振频率与温度的关系为式(3)中:ω(T)是温度为T时的陀螺谐振频率;m为检测质量块质量。

在温度T0附近的小范围内,式(3)可以线性近似为

陀螺谐振频率的漂移,对陀螺驱动模态和检测模态都有影响[5],陀螺信号的振幅和相位都会随谐振频率而改变。
从陀螺结构看,要减小温度变化对谐振频率的影响,须采用性能更好的材料,这将较大地增加成本[6]。并且即使环境温度不发生大的改变,陀螺自身工作较长时间,其内部温度也会发生变化。因此,有必要采取温度控制或者温度补偿措施来消除这种误差[7]。
2 灰色理论建模
通过对灰数进行灰运算、灰生成,以建立起灰色模型,通过模型再对客观事物进行预测、控制、优化等,这一套方法体系称之为灰色理论。
将状态估计与不良数据辨识理论作为数据预处理技术应用于灰色系统建模,以观测数据为依据进行状态估计,避免了常规建模中观测数据与实际数据同等对待的弊端。对数据作检测与辨识,使剔除不良数据后的状态估计结果更为精确,以提高灰色系统建模精度。
2.1灰色预测模型
灰色模型是灰色理论中最基本的模型。灰色理论建模过程一般用原始数据列做生成操作,而后建立微分方程并求解[8]。GM(m,n)模型中,m表示微分方程的最高阶数,n表示变量数。当n≥2时,所建GM模型不能做预测用。GM(1,1)是灰色模型中应用最为广泛的预测模型,其实质是求解单序列的一阶线性动态微分方程。用GM(1,1)对陀螺输出进行处理,步骤如下。
1)生成累加数列。设原始数列为

对原始数列进行m次累加操作,生成新的数列为:
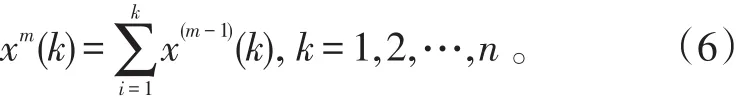
多次试验表明,在对MEMS陀螺进行累加生成时进行一次累加操作就可以产生规律性,生成的数列为

当数据规律不明显时,可增加累加次数。

模型参数运用最小二乘法计算得到:

式(9)中:

3)求解微分方程。白化形式一阶微分方程的解为


式(13)中:
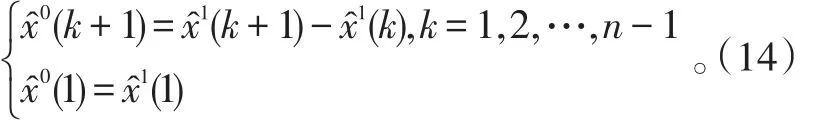
在对陀螺输出进行处理时,每增加一个新的信息,便将其加入到0中,同时去掉一个最老的信息以保持数列的维数不变,再建立新数列的灰色模型用于预测。
2.2数据预处理
将微机械MEMS置于转台上,通电一段时间记录陀螺输出,选取其中一只陀螺输出,利用GM(1,1)模型对其处理,取步长n=200,建立等维信息模型。可以看出,通过该模型处理后,陀螺输出噪声得到了明显的抑制。图1为原始数据输出和经灰色模型处理后的陀螺输出对比。利用灰色模型进行预处理后,可以减小数据的噪声,有助于精确建立模型。
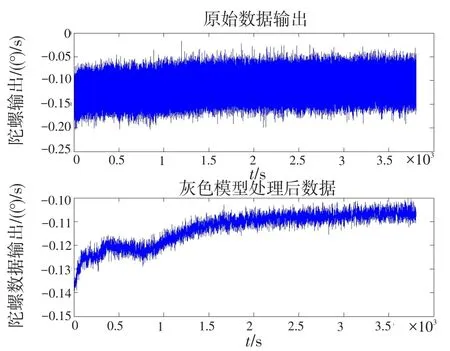
图1 灰色模型处理后与原始陀螺数据输出对比Fig.1 Original groscope output data comparing with the data disposed bgramodel
3 补偿算法
本文采用全温测试方法,所用MEMS陀螺能同时输出速率信号与温度信号,在-20℃、-10℃、0℃、10℃、20℃、30℃、40℃、50℃、60℃环境温度下,每个温度点保温2 h,然后采集陀螺输出信号与温度输出信号。
从图2可以看出,在不同的温度点,陀螺零偏有较大波动。

图2 陀螺零偏与温度关系曲线Fig.2 Relationship curve between the groscope zero offset and temperature

通过大量的试验分析,文中提出了一种基于灰色模型和多项式拟合[9]的温度补偿方法,即先将原始数据进行灰色模型处理后,再进行多项式拟合。式(15)、(16)中:Bias(t)为各温度点下陀螺的零偏;t为陀螺工作时间;T0为陀螺启动时刻的温度;a(T0)、b(T0)、c(T0)、d(T0)、e(T0)为拟合热系数,通过最小二乘法可确定该系数;Ai、Bi、Ci、Di、Ei(i=1,2,3,4)为拟合系数,通过不同温度下的a、b、c、d、e进行最小二乘拟合可以确定。
实际应用中,对每个陀螺通过高低温试验,求出Ai、Bi、Ci、Di、Ei后,可以将其固化在内部DSP系统中,在陀螺开机后测出陀螺温度,即可以通过公式(15)估计出陀螺当前零偏;然后,再从陀螺实测零偏中减去该估计出的零偏,就可以得到补偿后的零偏:式(17)中:Uc(Ti)为补偿后的零偏;U(Ti)为陀螺实测零偏;Bias(Ti)为估计出的零偏。
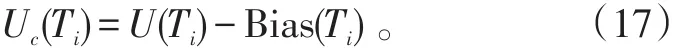
4 试验结果分析
试验是在高低温三轴转台上进行,温箱控制范围为-20~80℃,完全可以满足试验要求。在-20℃、-10℃、0℃、10℃、20℃、30℃、40℃、50℃、60℃环境温度下,每个温度点保温2 h,然后采集陀螺输出信号与温度输出信号。先对测试得到的原始数据进行灰色模型预处理;然后,根据式(15)编程,得到式(15)中拟合系数,如表1所示。
利用表1中的系数,根据式(16),利用最小二乘法拟合得到表2中拟合系数。

表1 模型中拟合热系数Tab.1 Fitting thermal coefficients in the model

表2 模型中拟合系数Tab.2 Fitting thermal coefficients in the model
利用表2中系数和式(16)便可以对陀螺进行实时补偿,在-20~60℃范围内,对陀螺仪零偏进行测试,结果如图3所示。由图3可知,经过补偿后,陀螺仪在-20~60℃的温度范围内零偏值有大幅减小。在25℃做了零偏测试试验,测试时间为1 h,陀螺仪零偏稳定性由原来的70 (°)/h,变为20 (°)/h,取得了比较理想的补偿效果,如图4所示。

图3 陀螺仪零偏与温度关系曲线Fig.3 Relationship between the groscope zero offset and temperature

图4 补偿前后陀螺输出Fig.4 Output of the groscope before and after compensation
分别对补偿前后求取零偏可以得到补偿前零偏为0.112 890 7 (°)/s,补偿后零偏为0.395 7×10-4(°)/s,大大提高了陀螺零偏,得到了显著的补偿效果。
5 结论
针对原始数据噪声较大,提出了一种基于灰色模型的温度补偿方法。即原始数据先通过灰色模型进行预处理,然后根据灰色模型处理过的数据,建立一种补偿模型,并用该模型对测试的数据进行预测补偿。试验表明,采用该方法使陀螺零位在全温范围内稳定精度提高了一个数量级,证明了提出方法的可行性和有效性。
参考文献:
[1]MICHAEL I FERGUSON,DIDIER KEMEULEN,CHRIS PEA,et al. Effect of temperature on MEMS vibratorrate groscope[C]//Aerospace Conference. IEEE. 2005:1-5.
[2]周斌.微机械陀螺数字化技术研究[D].北京:清华大学,2003. ZHOU BIN. Research of MEMS-groscope’s digital technolog[D]. Beijing:Tsinghua Universit,2003.(in Chinese)
[3]HONG K S. Compensation of nonlinear thermal bias drift of resonant rate sensor using fuzzlogic[J]. Sensors and Actuators,1999,78:143-148.
[4]SHCHEGLOV K,EVANS C,GUTIERREZ R,et al. Temperature dependent characteristics of the JPL silicon MEMS groscope[C]//Aerospace Conference Proceedings. IEEE. 2001:403-411.
[5]温祖强,钱峰.微机械陀螺温度特性及其补偿算法研究[J].电子测量技术,2011,34(1):51-54. WEN ZUQIANG,QIAN FENG. Research of thermal characteristic and compensation algorithm for MEMS-groscope[J]. Electronic Measurement Technolog,2011,34 (1):51-54.(in Chinese)
[8]李士心,王晓亮,翁海娜,等.基于灰色模型和RBF神经网络的MEMS陀螺温度补偿[J].中国惯性技术学报,2010,18(6):742-746. LI SHIIN,WANGIAOLIANG,WENG HAINA,et al. Temperature compensation of MEMS groscope based on gremodel and RBG neural network[J]. Journal of Chinese Inertial Technolog,2010,18(6):742-746.(in Chinese)
[9]张琬琳,尹剑,郭栓运,等. Q-MEMS陀螺零偏补偿技术研究[J].应用光学,2010,31(4):549-551. ZHANG WANLIN,IN JIAN,GUO SHUANUN,et al. Temperature compensation for Q-MEMS gro[J]. Journal of Applied Optics,2010,31(4):549-551.(in Chinese)
Temperature Compensation of MEMS Groscope Based on GraModel
Abstrraacctt:: The temperature influence mechanism to the zero offset was analzed in this paper firstl, and then according to the problem of the environment temperature leading to the bigger zero output bias of MEMS groscope, a temperature com⁃pensation method based on gramodel was presented. This method firstlpre-handled the original data through gramod⁃el, then a compensation model based on the data after pre-handled was built, and this model to compensate the test data was used. The eperiment results showed that the stabilitaccuracof the groscope’s zero position was improved to a high level in the full temperature range which also showed the feasibilitand validitof the proposed method.
Temperature Compensation of MEMS Groscope Based on GraModel
作者简介:李翊(1977-),男,工程师,硕士。
基金项目:国家自然科学基金资助项目(61174031)
收稿日期:2014-11-26;
DOI:10.7682/j.issn.1673-1522.2015.02.015
文章编号:1673-1522(2015)02-0165-04
文献标志码:A
中图分类号:TP273.4
修回日期:2015-01-16

