立体几何问题教学之点滴体会

张凯

在数学教学实践中，教师们深感立体几何教学中存在着投入多、收效少的问题，极大地影响了学生数学素质的提高。原因到底出在哪儿呢？笔者认为主要是我们的教学未能充分调动学生学习的积极性，未能引导学生带着问题学习，致使学生的思维经常处于被动的状态。为了引导学生带着问题学习，在新课引入环节就要把问题交给学生，使每一个学生都能了解问题是怎样提出的，具体内容是什么。

一、通过观察实物或模型提出问题

例如，在讲异面直线时，先让学生观察摆在同一平面内的两条不重合的直线的两种位置，指出只要是平行或相交的两条直线就一定在同一平面内，接着把两条直线摆成如图一的位置，问：直线a，b还在同一平面内吗？从而提出异面直线的概念。学生观察图一得出异面直线的定义：不同在任何一个平面内的两条直线叫做异面直线。我接着提出一个问题：分别在两个平面内的两条直线是否为异面直线？一部分学生认为“是”，于是我画出分别在两个平面内的两条相交直线和两条平行直线，学生得出分别在两个平面内的两条直线不一定是异面直线的结论。我借机强调指出，两条异面直线是不可能在同一平面内的。这样，学生就进一步理解了上述概念，认识到两条异面直线定义的本质。

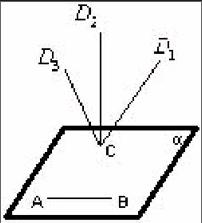
又如，在讲两条异面直线所成的角时，由于受思维定势的影响，一提到角学生就会想到由一点出发的两条射线，于是我先让学生观察如图二所示的模型，由不同颜色的细棒摆出CD1、CD2、CD3等位置，在学生看出每一条与AB都是异面直线后提出

问题：它们与AB的位置关系虽然都是异面，但是否有不同呢？学生会注意到，它们中的每一条与AB的倾斜程度不一定相同，于是头脑中形成了一个类似于平面几何中的“角”的概念。此时，可以让学生进一步思考：由于两条异面直线并不相交，没有类似平面几何中的角的顶点的东西，那么怎样来描述这个角呢？然后再引出两条异面直线所成的角的概念。

以上做法充分调动了学生大脑中的空间感知信息，因此确立概念的过程比较顺利，学生的印象自然也比较深刻。这种由学生观察实物或模型从中提出问题并建立立体几何概念的方法，能够引起学生的认知冲突，达到排除平面定势干扰的目的。

二、由知识本身发展的必然性提出问题

在学生理解了直线和平面垂直的定义后教师应指出，在实际问题中往往需要我们去判断一条直线是否与一个平面垂直，当定义无法提供判断的依据时，我们就需要寻找判定定理。明确这些之后再研究直线与平面垂直的判定定理，学生就觉得很有必要了。

例如，在讲授直线和平面平行的判定定理时，我是这样引入新课的：现有a∥b（两直线平行），平面α过b，a和α的位置关系怎样？请使用教具自主探究。然后接着让学生思考：欲使两直线平行转化为直线和平面平行，还需添加什么条件？最后，由学生总结得出结论，这样直线和平面平行的判定定理就自然而然地引出来了。

三、用类比的方法提出问题

立体几何中的许多结论都可以由平面几何的性质类比得出，这类例子较多，如平行公理、等角定理等。

平面几何图形里点和直线的性质与立体几何图形里直线和平面的性质相类似，我们可以看作它们是从平面图形中的点和直线分别扩展到立体图形中的直线和平面。

当然也要注意，平面图形的有些性质推广到空间图形时，由于领域扩大了，所以未必能够成立。如下列几个平面几何的命题就容易与立体几何时相混淆。（1）两直线不平行则相交。（2）两直线同垂直于一直线，那么这两条直线互相平行。（3）经过一点可以做一条直线并且只可以做一条直线和另一条直线垂直。

以上就平面几何与立体几何知识做了一些类比研讨，立体几何知识本身也可以用类比思维进行教学。例如，可以围绕有关距离的概念进行类比，以便更好地区分点与面的距离、线与面的距离、面与面的距离等概念，把握他们的本质特征，了解它们之间的相互转化关系，掌握了解这类问题的基本思维方法。

要想让学生带着问题学习数学，就要注重发挥教师的主导作用，体现学生的主体地位，激发学生的求知欲，放手让学生读一读、想一想、议一议、练一练，这样学生才能获得“真知识”，而不是“假知识”，获得“活知识”，而不是“死知识”，学生的探究能力才能进一步提高。

（责任编辑 赵永玲）