双向二维局部保持鉴别投影应用于人脸识别

周慧，陈熙，刘增力

昆明理工大学信息工程与自动化学院，昆明650500

双向二维局部保持鉴别投影应用于人脸识别

周慧，陈熙，刘增力

昆明理工大学信息工程与自动化学院，昆明650500

双向二维局部保持映射（双向2DLPP）与二维局部保持映射（2DLPP）比较，双向2DLPP同时对图像的行方向和列方向进行降维处理，可以采用较少的系数有效地表示图像。为了进一步增强双向2DLPP算法的分类能力，将双向2DLPP所提取的特征采用线性判别式分析（LDA）进行分类，从而形成了一种新的监督算法：鉴别双向二维局部保持投影。理论分析表明，无论在计算量还是内存要求方面，所提鉴别双向二维局部保持投影算法比双向2DLPP和主成分分析+线性判别式分析（PCA+LDA）要少，而且在ORL和Yale数据库上的人脸识别实验表明，新算法的识别性能比双向2DLPP和PCA+LDA算法要好，且具有较少的计算复杂度。

双向二维局部保持映射；线性判别式分析；人脸识别；计算复杂度

1　引言

局部保持映射［1］（LPP）是一种广泛应用于模式识别，计算机视觉等领域的线性数据降维技术。在LPP中，二维图像矩阵首先必须转换成一维向量，但是将图像转化成向量就失去了图像本身的结构特性，同时转化后的向量维数很高，这就容易导致计算复杂度太大。为了解决这个问题，二维局部保持映射［2-3］根据局部保持准则直接从图像矩阵中提取特征。文献［4-5］中的实验表明采用2DLPP进行人脸识别的识别率要高于LPP，同时计算复杂度要小得多。然而，2DLPP进行特征表示所需的系数很多，例如，假设一幅图像大小是128×128，那么2DLPP中所需的表示系数为128×d，通常为了得到较高的识别率，d应该大于5。为了减少表示系数，可以同时在行方向和列方向对图像进行降维处理，从而提出了二方向二维局部保持映射［6］（（2D）2LPP）。二方向二维局部保持映射在数据降维时强调的是数据的局部结构，而实际中很多情况下降维后需要对数据进行分类，于是将提取的特征交给LDA进行分类，从而形成了一种新的监督算法：（2D）2LPP+LDA。ORL人脸数据库［7］和Yale数据库［8］上的人脸识别试验表明（2D）2LPP+LDA具有比（2D）2LPP更好的人脸特征提取和分类能力，而理论分析表明（2D）2LPP+LDA在计算量和内存要求方面比PCA+LDA要少。

2　鉴别双向二维局部保持映射

2.1行方向二维局部保持映射

假设a是一个n维单位列向量，Xi表示一幅m行n列的图像，在一维LPP算法中Xi必须先转化成一个m×n维的向量，但是在2DLPP算法中，可以直接将图像Xi投影到单位列向量a上，如式（1）所示：

Yi就是所谓的投影特征向量，它实际上是图像Xi在垂直方向上的投影。给定一个训练样本集T=｛X1，X2，…，XN｝，则2DLPP的目标函数为：

Wij是图像Xi和Xi之间的相似度，Wij可按式（3）计算。

下面根据2DLPP的目标函数，通过矩阵运算推导2DLPP投影矩阵的计算方法。

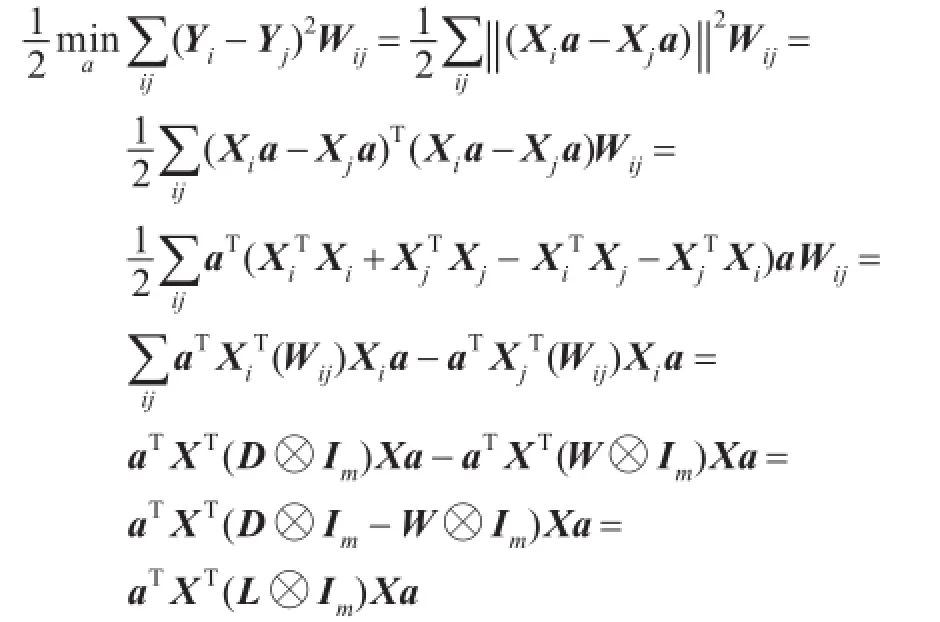
在上面的推导中X是一个mN×n的矩阵，它是通过在列方向排列所有图像矩阵得到的，即：， D是一个对角矩阵，。L=D-W是拉普拉斯矩阵。Im是一个m阶单位矩阵。操作符⊗表示克罗内克积［9］，通过使用克罗内克积，L⊗Im可表示为：

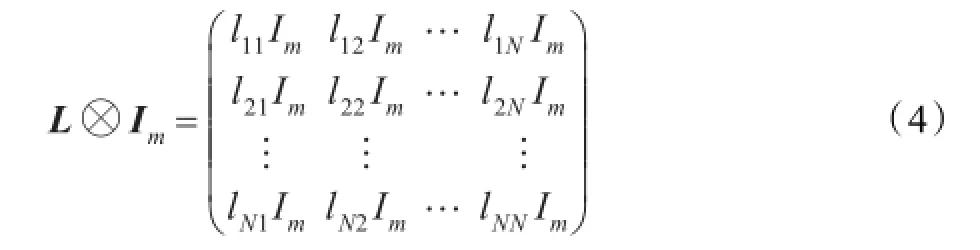
此式中lij（ i，j=1，2，…，N）表示矩阵L的元素。很明显，当a为零向量时，总是达到最小值0，为了防止出现这种情况，增加一个限制条件：aTXT（D⊗Im）Xa=1，因此2DLPP的目标函数变为：

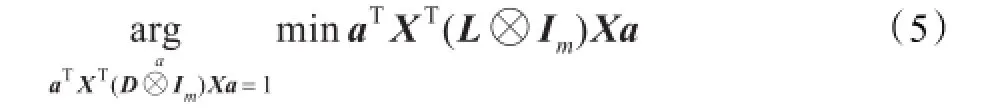
最小化上述目标函数的变换向量a就是广义特征值问题（6）最小特征值所对应的特征向量。

通常一个变换向量不足以把所有模式分开，故一般选取最小d1个特征值所对应的特征向量构成投影矩阵，投影矩阵的每一列就是一个特征向量。数据从高维到低维的映射可以表示为：

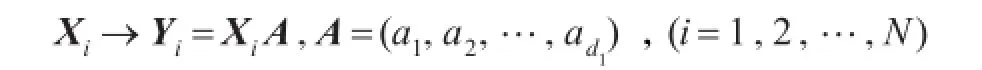
2.2列方向二维局部保持映射

假设b是一m维单位列向量，Xi表示一个大小为m×n的图像矩阵，将图像矩阵直接投影到向量b上得：

所得n维向量Yi就是列方向投影特征向量。与上节类似，通过矩阵运算，列方向2DLPP最小化目标函数（2）可以表示为：

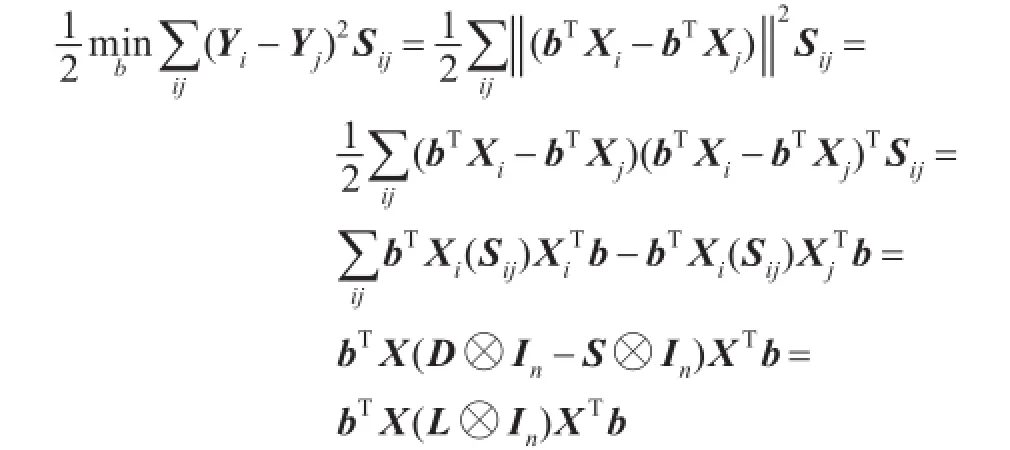
这里X是一个m×nN的矩阵，它是通过在行方向排列所有图像矩阵得到的，即：X=［X1，X2，…，XN］，D是一个对角矩阵，是拉普拉斯矩阵。In是一个n阶单位矩阵。操作符⊗表示克罗内克积，通过使用克罗内克积，L⊗In可表示为：

上式中lij（ i，j=1，…，N）表示矩阵 L的元素。与前面类似，增加一个限制条件：bTXT（D⊗Im）Xb=1，因此列方向2DLPP的目标函数变为：

矩阵X（L⊗In）XT和X（D⊗In）XT都是对称正半定矩阵。最小化列方向2DLPP目标函数的变换向量b就是广义特征值问题（10）最小特征值所对应的特征向量。

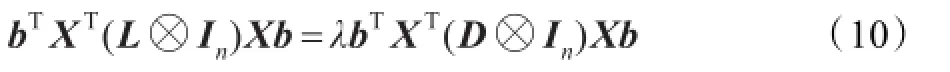
通常一个变换向量不足以把所有模式分开，故一般选取最小d2个特征值所对应的特征向量构成投影矩阵，投影矩阵的每一列就是一个特征向量。数据从高维到低维的映射可以表示为：Xi→Yi=BTXi，B=（b1，b2，…，bd2）。

2.3鉴别双向二维局部保持映射

前面2.1和2.2节分别对行方向和列方向二维局部保持映射的基本原理进行了较详细的阐述，无论行2DLPP还是列2DLPP都存在表示系数太多的缺陷，如果对图像矩阵同时进行和列二个方向上的2DLPP运算，则可以用较少的系数表示一幅图像。假设行方向2DLPP从训练图像中学习到一个投影矩阵A，那么一个m行n列图像Xi投影到这个矩阵上产生一个m行d1列的矩阵AXi。类似地，列方向2DLPP学习到一个投影矩阵B，将图像Xi投影到这个矩阵上产生一个d2行n列的矩阵BTXi。假设同时得到了投影矩阵A和B，那么将图像Xi同时投影到这两个矩阵上得：

Ci也可称为图像表示的系数矩阵，图像重建可以表示为：。

为了进一步增强（2D）2LPP的分类能力，设计鉴别双向二维局部保持投影算法（（2D）2LPP+LDA）。该算法由2步构成，首先在考虑数据局部特性的基础上采用（2D）2LPP进行降维，得到每一幅图像的投影系数矩阵Ci（i=1，2，…，N），接着将投影系数矩阵Ci转化成向量后Di进一步采用LDA降维。设由LDA产生的投影矩阵为FLDA（其大小为（d1×d2）×l），则对于每幅图像Xi（i=1，2，…，N），由（2D）2LPP+LDA产生投影向量Fi=Di×FLDA（i=1，2，…，N）。现假设一幅测试图像XT，其相应投影向量为FT，则FT与任意一幅训练图像Fi投影系数矩阵之间的距离可以表示为：

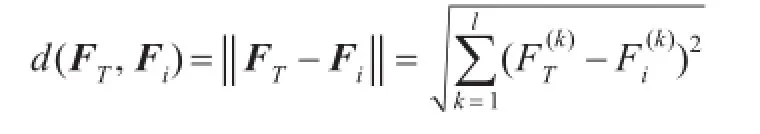
3　试验与分析

在这一章将比较所提新算法与局部保持映射、正交局部保持映射［10］（OLPP）、核局部保持映射［11］（KLPP）、双向二维局部保持投影和线性判别式分析［12］（PCA+LDA）在ORL和Yale人脸数据库上人脸识别性能。式（3）中的最近邻数为每类样本数，考虑到（2D）2LPP+LDA是一种监督算法，故加权矩阵W采用监督方式，即只有同类样本之间的权值按式（3）计算，不同类样本之间的权值为0。为简单起见，采用基于欧式距离的最近邻分类器进行分类。

3.1数据库

ORL数据库包含40个人的人脸图片，每个人10张。某些图片是在不同时间拍摄的，图片之间存在各种变化，例如表情（睁眼和闭眼、笑和不笑）和面部细节（戴或不戴眼镜）。一些图片还有20度内的旋转变化。图1（a）是该数据库中2个人的20张样本图像。Yale人脸数据库包含15个人的165张灰度图片，每个人11张。图片主要有光照、表情和戴不戴眼镜方面的变化。图1（b）是该数据库中2个人的22张样本图像。所有图像的大小都调整到32×32。

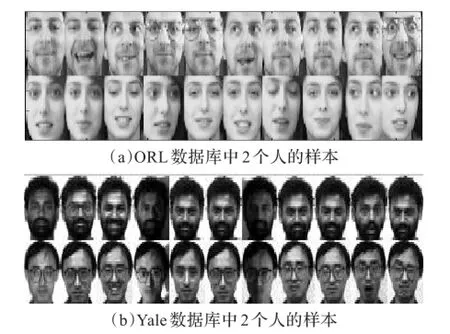
图1　预处理样本图像

3.2正确识别率与特征维数的关系

首先考察了正确识别率与特征维数的关系，随机地分别从ORL和Yale数据库中每人选择5个样本图像组成ORL和Yale训练图像集，剩下的为各数据库的测试图像集。实验重复10次，图2（a）和（b）中画出了在ORL和Yale数据库中不同特征维数下的平均识别率。

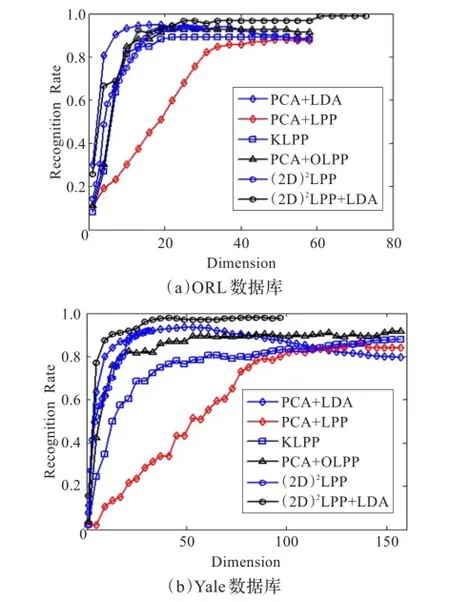
图2　正确识别率与特征维数的关系

在ORL数据库中，（2D）2LPP+LDA首先采用（2D）2LPP将原数据降维到10×10，然后再采用LDA继续降维，故在这种算法中，考察的特征维数是从1至100，而对于LPP、OLPP和PCA+LDA三种算法首先都是采用PCA将数据维数降到60，然后分别采用LPP、OLPP和LDA进行降维，故考察的特征维数都是从1到60。对于KLPP，首先采用核主成分分析［13-14］（KPCA）降到60维，然后采用LPP降维，故KLPP中最大可考察的维数为60。

在Yale数据库中，（2D）2LPP+LDA首先采用（2D）2LPP将原数据降维到10×10，然后再采用LDA继续降维，故在这种算法中，我们考察的特征维数可以是从1至100，为了较清楚的对比其他算法，我们在图2（b）中仅显示前75维的识别率，其余的特征维数所对应的识别率基本不变。而对于LPP、OLPP和PCA+LDA三种算法首先都是采用PCA将数据维数降到160，然后分别采用LPP、OLPP和LDA进行降维，故考察的特征维数都是从1到160。对于KLPP，首先采用KPCA降到160维，再采用LPP降维，故最大可考察的维数为160。

从图2（a）（b）中可以看出（2D）2LPP+LDA的平均最佳识别率是最高的，而且达到一定维数后识别率很稳定。对于（2D）2LPP算法，同时将行方向和列方向的维数从1变化到32维。

3.3正确识别率与训练样本集大小的关系

上一节考察了PCA+LDA、LPP、KLPP、OLPP和（2D）2LPP+LDA中正确识别率与特征维数的关系，这一节继续考察识别率与训练样本集大小的关系。首先随机从ORL和Yale数据库中每个人选择3，4，5，6，7，8个样本组成不同大小的ORL和Yale训练样本集，剩下的图片都作为各数据库的测试集。比较了PCA+LDA、LPP、KLPP、OLPP和（2D）2LPP+LDA几种算法在这些不同个数训练集上的识别性能，每个训练集上重复10次试验，表1和表2分别记录了在ORL和Yale数据库这些算法在不同训练集上的识别率及标准偏差。从表1和表2中可知，随着每类训练样本数增大，识别率都有所上升。在表中所列几种算法中，（2D）2LPP+LDA识别率是最好的，而且标准偏差较小，说明识别结果较稳定。

表1　ORL数据库上的平均识别率和标准偏差%

表2　Yale数据库上的平均识别率和标准偏差%

3.4计算复杂度与内存需求分析

本文所提算法和PCA+LDA都是监督算法，在前面一节比较了本文所提算法与PCA+LDA在识别率方面的性能，本节继续对PCA+LDA与（2D）2LPP+LDA的计算复杂度、内存需求进行比较分析。为了计算PCA+ LDA的投影特征空间，首先需要计算一个N×N的特征值问题，然后求解一个dPCA×dPCA的广义特征值问题，这里N是训练样本集的样本数，dPCA是PCA阶段的特征维数。然而，（2D）2LPP+LDA算法中在（2D）2LPP算法中需要求解一个m×m特征值问题和一个n×n特征值问题，然后在LDA阶段需要求解一个krow×kcol广义特征值问题，这里m，n，krow和kcol分别是原图像的行数、原图像的列数和（2D）2LPP中列方向2DLPP和行方向2DLPP降到的维数。由于一个M×M特征值问题的计算复杂度［15］为：O（M3），那么PCA+LDA投影矩阵的计算复杂度为，（2D）2LPP+LDA的计算复杂度为O（m3+n3+［max（krow，kcol）］3），假定m，n，dPCA和max（krow，kcol）都小于训练样本数，则（2D）2LPP+LDA比PCA+LDA需要更少的计算量计算投影矩阵。

下面继续分析将测试图像投影到PCA+LDA和（2D）2LPP+LDA特征空间所需的计算量，在这里假设这两种算法的最终投影特征空间维数相同，都为dLDA，则将Np幅测试图像投影到PCA+LDA特征空间所需的计算量为：Np×（m×n）×dLDA，而（2D）2LPP+LDA算法需要的乘法次数为：Np×［m×n×min（kcol，krow）+（krow×kcol）×max（m+dLDA，n+dLDA）］。在内存方面，PCA+LDA算法中仅需保存一个投影矩阵，大小为（m×n）×dLDA，而（2D）2LPP+LDA算法中需要保存三个特征矩阵，总的大小为：kcol×m+krow×n+krow×kcol×dLDA。表3总结了（2D）2LPP+LDA和PCA+LDA算法所需的计算量和内存要求。假设在ORL数据库上采用200个训练样本，如果m，n，krow和kcol分别取值30、30、10和10，N=200，dLDA=39，dPCA=160，d（2D）2LPP=10×10，则据表3可以看出（2D）2LPP+LDA算法无论在计算复杂度和内存需求方面都比PCA+LDA具有优势。

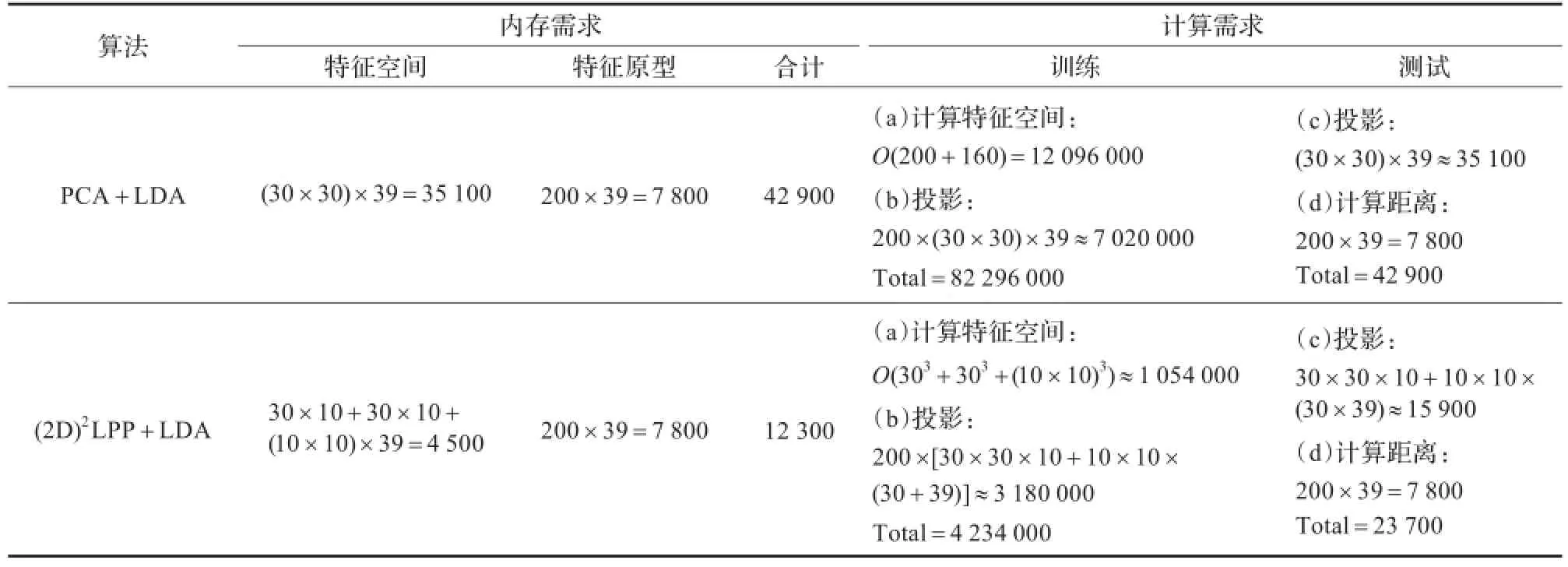
表3　（2D）2LPP+LDA和PCA+LDA在ORL数据库上的计算复杂度和内存需求比较

4　结束语

本文提出了一种有效的人脸识别算法：（2D）2LPP+LDA，（2D）2LPP与现在的2DLPP的主要区别在于后者是在行方向处理图像，而前者同时在行和列两个方向处理图像，这样就能用更少的系数进行特征表示，显著提高了识别速度，而（2D）2LPP提取的特征采用LDA分类进一步增强了算法的分类能力。ORL和Yale数据库上的人脸识别实验证实了所提算法的有效性。

［1］He X F，Niyogi P.Locality preserving projections［C］//Proc Conf Advances in Neural Information Processing Systems，2003.

［2］Chen S，Zhao H，Kong M，et al.2D-LPP：A two dimensional extension of locality preserving projections［J］.Neurocomputing，2007，70：912-921.

［3］孙丽娟，杨丹，张小洪，等.基于SR-2DLPP的人脸识别［J］.计算机应用研究，2009，26（7）：2789-2792.

［4］Ben N，Shiu S C K，Pal S K.Two dimensional Laplacianfaces method for face recognition［J］.LNCS RSCTC，2006.

［5］Zhang Zhiwei，Yang Fan.2DLPP：A novel method for small sample size faces recognition［J］.Journal of Optoelectronics· Laser，2008，19（7）：972-975.

［6］靳丽丽，陈秀宏.一种双向2DLPP算法及其在人脸识别中的应用［J］.计算机工程与科学，2010，32（9）：50-64.

［7］The ORL Face Database，Cambridge，U.K，AT&T（Olivetti）Research Laboratories［EB/OL］.［2013-05-05］.http：//www.uk. research.att.com/facedatabase.html.

［8］YaleUniv.Facedatabase［EB/OL］.（2002）.http：//cvc.yale. edu/projects/yalefaces/yalefaces.html.

［9］Jain A K.Fundamentals of digital image processing［M］.［S.l.］：Prentice Hall，2011.

［10］Cai D，He X，Han J，et al.Orthogonal laplacianfaces for facerecognition［J］.IEEETransactionsonImageProcessing，2006，15（11）：3608-3614.

［11］Feng G，Hu D，Zhang D，et al.An alternative formulation of kernel LPP with application to image recognition［J］. Neurocomputing，2006，69：1733-1738.

［12］Zhao W，Chellappa R，Phillips P J.Subspace linear discriminantanalysisforfacerecognition，TechReport CAR-TR-914［R］.Center for Automation Research，University of Maryland，1999.

［13］Kim K I，Jung K，Kim H J.Face recognition using kernel principal component analysis［J］.IEEE Signal Processing Letters，2002，9（2）：40-42.

［14］Yang Jian，Zhang D.Two-dimensional PCA：A new approach to appearance-based Face representation and recognition［J］. IEEE Trans on PAMI，2004，226（4）：131-137.

［15］Golub G H，Van Loan C F.Matrix Computation［M］.3rd ed. Baltimore，MD：The Johns Hopkins Univ Press，1996.

Discriminant bidirectional two-dimensional local preserving projection and its application in face recognition.

ZHOU Hui，CHEN Xi，LIU Zengli

School of Information Engineering andAutomation，Kunming University of Science and Technology，Kunming 650500，China

Recently，bidirectional two-dimensional Local Preserving Projection（2DLPP）is proposed for face representation and recognition.Compared with two-dimensional Local Preserving Projection（2DLPP），the main idea behind bidirectional 2DLPP is that bidirectional 2DLPP simultaneously considering the row and column directions of images.Bidirectional 2DLPP needs fewer coefficients for image representation than 2DLPP which essentially works in the row direction of images.Furthermore，to enhance the classification ability of bidirectional 2DLPP，a new supervised algorithm is proposed:bidirectional 2DLPP plus LDA，in which images preprocessed by bidirectional 2DLPP are processed by LDA.Theoretical analyses show that bidirectional 2DLPP plus LDA algorithm has advantages over PCA+LDA，2DLPP and bidirectional 2DLPP in computation complexity and memory requirements.The results of face recognition experimental on ORL and Yale face databases also show good performance of the methods with less computation.

discriminant bidirectional two-dimensional local preserving projection；linear discriminant analysis；face recognition；calculation complexity

A

TP391.41

10.3778/j.issn.1002-8331.1311-0027

国家自然科学基金（No.61262040，No.61271007）；云南省应用基础研究计划项目（No.KKSY201203062）。

周慧（1989—），女，硕士，主要研究方向为图像处理、模式识别、压缩感知等；陈熙（1976—），通讯作者，男，副教授，主要研究领域为生物特征识别与信息安全。E-mail：xcbiometrics@126.com

2013-11-03

2014-01-07

1002-8331（2015）22-0163-05

CNKI网络优先出版：2014-04-01，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0027.html