生物地理学算法求解柔性车间作业调度问题

吴定会，孔飞，朱绍文，纪志成

江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122

生物地理学算法求解柔性车间作业调度问题

吴定会，孔飞，朱绍文，纪志成

江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122

针对加工设备和操作工人双资源约束的柔性作业车间调度问题，建立以生产时间和生产成本为目标函数的柔性作业车间调度模型，提出基于模糊Pareto支配的生物地理学算法，采用模糊Pareto支配的方法计算解之间的支配关系并对Pareto解集排序，进行全局最优值的更新，并采用余弦迁移模型来改善生物地理学算法的收敛速度。将该方法应用于某模具车间的柔性作业车间调度中，仿真结果验证了该方法的可行性和有效性。

柔性作业车间调度；模糊Pareto支配；生物地理学算法；余弦迁移模型；双资源约束

1　引言

车间作业调度是影响车间生产效率的关键因素，它采用有效的调度优化技术，在一定的约束条件下，合理地分配现有的人力和物力资源，完成给定的任务，满足生产过程中经济上或性能上的目标［1］。其中柔性作业车间调度问题（Flexible Job Shop Scheduling Problem，FJSP）突破了传统作业调度资源唯一性的限制，更符合生产实际，因此研究FJSP具有重要的理论意义和实际价值。

在实际生产中，车间调度问题通常是同时对多个目标进行优化。目前求解柔性作业车间多目标调度方法可分为两类：（1）单目标优化法。通过赋予每个目标不同的权重系数将多目标问题转换为单目标问题。文献［2］提出基于蚁群与邻域搜索算法的混合算法，以生产周期、设备总负荷和关键设备负荷为目标，对柔性作业调度问题进行了研究。文献［3］提出多智能体免疫算法，以生产周期和客户满意度为目标，对存在批量可变性、机器并行性、加工时间和交货期模糊性的生产问题进行了研究。这类方法的缺点在于过分依赖权重参数，难以收敛到Pareto最优沿面的非凸区域。（2）Pareto优化策略。采用Pareto最优的概念评价解的优劣，将优化目标转化为寻找一组符合评价标准的Pareto解。文献［4］提出了一种基于Pareto支配的混合粒子群优化算法，引入了基于Baldwinian学习策略和模拟退火技术相结合的多目标局部搜索策略，增强了算法的探索性，达到最小化完工时间、设备总负荷和单台设备总负荷最小化的目标。文献［5］提出改进的非支配排序遗传算法，在考虑设备、操作人员资源约束下，求以加工成本、客户满意度及生产总流程时间为目标的柔性车间模糊调度。文献［6］结合免疫遗传算法和约束理论提出了一种基于瓶颈工序的多资源多目标车间调度算法，克服了多目标遗传算法早熟及Pareto解集多样性不足等缺陷。

目前，柔性作业车间调度问题求解主要集中在运用遗传算法［7-8］、粒子群算法［9-10］和蚁群算法［11-12］等，通过迭代实现柔性作业车间调度方案优化。Dan Simon在2008年提出一种新的启发式算法-生物地理学BBO（Biogeography-Based Optimization）算法［13］，它通过模拟自然界不同栖息地种群数量的变化过程寻找优化问题的最优解。与蚁群优化算法、遗传算法和粒子群算法优化相比，生物地理分布优化算法的主要优点是参数少、实现简单、收敛速度快、搜索精度高，可以有效地解决全局优化问题。目前，BBO算法已经用于解决卫星图像分类问题［14］、离散优化问题［15］、电力系统多目标发电调度问题［16］等。Rahmati等提出将生物地理学的优化方法应用于柔性车间调度［17］，并与GA、EGA、KEGA优化算法进行对比，结果表明BBO算法具有更好的稳定性及收敛性，但是仅考虑设备单一资源约束的作业调度问题。

本文针对设备和工人双资源约束的柔性车间作业调度问题，提出了基于Pareto支配的生物地理学调度算法（ParetoDominance-CombinedBiogeography-Based Optimization Scheduling Algorithm，FPDCBBO），使用模糊Pareto支配的方法计算解之间的支配关系并对解集排序，促进Pareto最优前沿向理想Pareto前沿逼近，然后采用余弦迁移模型改善算法的收敛速度，最后运用该算法解决某模具公司的柔性作业调度问题。

2　柔性作业车间调度模型

2.1问题描述

本文用产品零件集N，工序集J，工序加工时间集T，设备集M、工人集P、工序与设备关系集J_M、设备与工人关系集M_P和调度目标F来描述离散制造车间作业调度数学模型。

（2）工序集O，每个零件有若干个具有先后约束的工序，工序集包括工序序列集O和工序属性集OG。，其中O为调度任务的总工序数，Oi表示零件i总工序数，Oij表示第i零件的第j道工序。定义工序Oij的工序属性参数组集，第j个加工属性参数组，G1为工序需要配备的设备，G2为所需的操作人员。

（3）资源集包括设备集M和操作人员集P。具体如下：M=｛mi|1≤i≤M｝，其中M为车间可用的设备总数，其负载量和状态用Ci和Si描述。状态Si=0和1分别表示设备处于空闲和忙碌状态。P=｛Pi|1≤i≤P｝，P为车间内操作人员总数，Pi为第i操作人员的工号，工作时间为Ti，状态Si=0和1时分别表示操作人员处于空闲和忙碌状态。

（4）工序与设备的关系集O_M，O_M=｛OMijk|1≤i≤N，1≤j≤Oi，1≤k≤M｝，其中OMijk=0或1，分别表示工序Oij是否可以在设备Mk上加工。设备与操作人员的关系集M_P。M_P=｛MPij|1≤i≤M，1≤j≤P｝，其中MPij=0或1，分别表示操作人员Pi是否可以操作设备Mj。

（5）工序加工时间集，即工序在不同设备上的加工时间，T=｛Tijm|1≤i≤N，1≤j≤Oi，1≤m≤M｝，其中Tijm表示零件i的第j道工序在设备m上的加工所需时间。

2.2数学模型

本文在满足工艺约束前提下，给出了以下目标：完工时间F1最小化；总生产成本F2最小化。其中F2包括设备加工成本和工人成本。车间作业调度的数学模型如下。

首先定义如下的参数和变量：Ci为零件i的完工时间，Cij为零件i的j道工序的完工时间，Cijm为零件i的第j道工序在设备m上的完工时间，Sij为零件i的工序j可以开始加工的时间，Tij为零件i的工序j加工时间，Tijm为零件i的第j道工序在设备m上的加工时间，Em为设备m的单位加工时间动力燃料费用，Zm为设备m的折旧费用，Sp为工人p单位时间的人员成本，Xijmp为零件i的第j道工序在设备m上加工，并且设备m由工人p操作时为1，否则为0，Fihkp为零件i的第h道工序在设备k由工人p加工的完成时间，Tijmp为零件i的第j道工序在设备m由工人p加工的时间，Sihkp为零件i的第h道工序在设备k由工人p加工的开始时间，Rijabm为设备m上加工工序j和b的判别条件，i和b都在设备m上加工时，如果零件i的第j道工序先于零件a的第b道工序，则Rijabm=1，否则Rijabm=0。

目标函数：

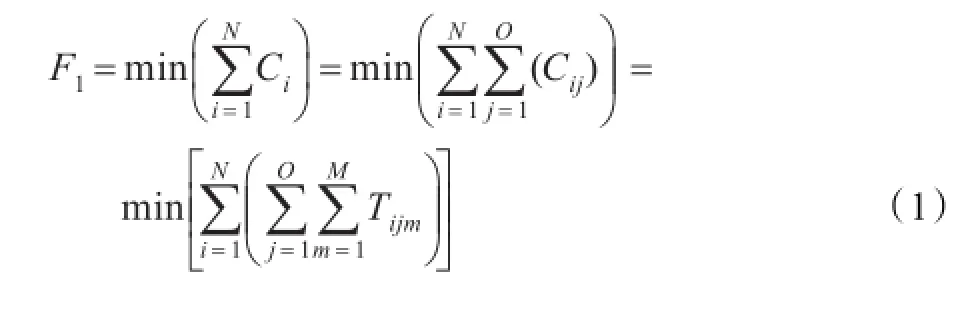
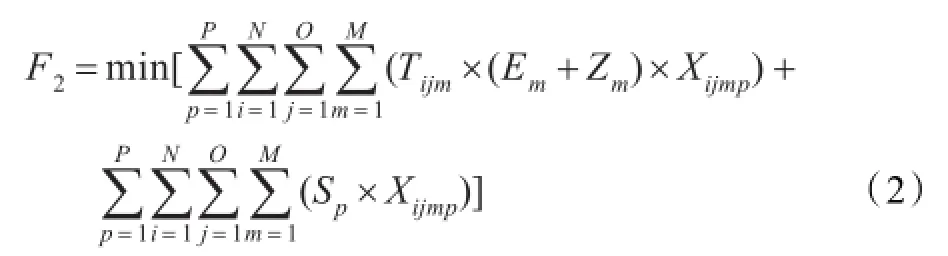
约束条件：

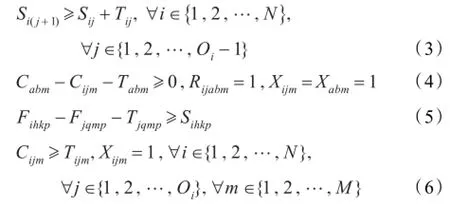
式（3）保证了一个零件只能在加工完成前一道工序后才可以加工后一道工序；式（4）保证了设备m不能同时加工两个不同的工序；式（5）保证一个工人不能同时操作两台设备；式（6）保证任何一道工序的完工时间不能小于其加工时间。

3　多目标预备知识

3.1模糊Pareto支配

He Z等人提出的模糊Pareto进化方法［18］求解Pareto解之间的支配关系，更接近支配的原始概念，在处理多目标优化问题时具有较好的实用性。首先给出3个定义。

定义1（模糊集）对于研究范围X中的任一元素x，都有一个数A（x）∈［0，1］与之对应，则称A是X上的模糊集，A（x）称为x对模糊集A的隶属度。隶属度A（x）接近1，表示x属于A的程度越高，反之，越接近0，x属于A的程度越低。当x在X中变动时，A（x）就是一个函数，称为A的隶属函数。FG（x）的计算公式如式（7）所示：

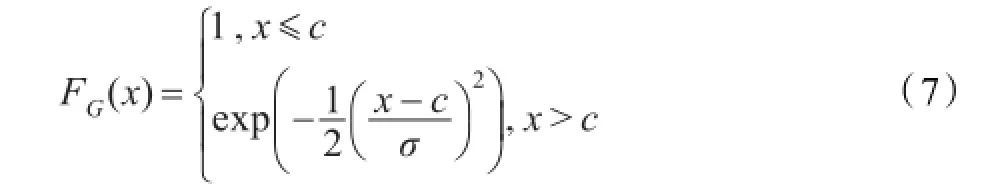
其变化范围是0到1，c=-1，σ=0.5，x的计算公式如式（8）所示：

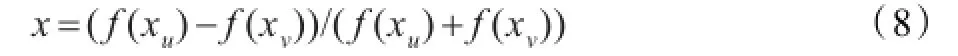
xu和xv为目标函数f上的两个解向量。对于最小化问题，如果f（xu）＜f（xv），则x≈-1，FG（x）≈1对应于Pareto支配关系，可以说明xu支配xv。反之，f（xu）＞f（xv），则x≈1，FG（x）≈0对应于Pareto支配关系，可以说明xu被xv支配。

定义2（模糊Pareto支配）对于Nobj个最小化问题，给定两个解向量xu和xv，存在u=f（xu）=（u1，u2，…，uM）和v=f（xv）=（v1，v2，…，vM），定义p（u）=u-v，p（v）=v-u，利用高斯型隶属度函数使FG（p（u））→［0，1］和FG（p（v））→［0，1］，即和φ（v）=FG（p（v））=。则向量u的模糊值为，向量v的模糊值为若，则称x模糊支配x即xx。uvuv

定义3（模糊适宜度值）存在n个解向量，利用高斯型隶属度函数分别计算出每个解向量与其他n-1个解向量的模糊值，然后通过公式（9）分别计算两个解向量之间的模糊支配度，将n-1个模糊支配度相加后除以n-1得到的值，作为每个解向量的模糊适宜度值FFM。

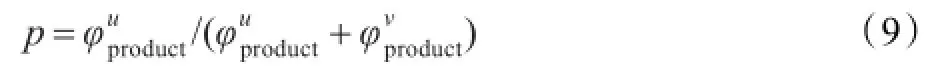
3.2解的拥挤距离

在解空间上，某个体周围个体的分布密度越小，拥挤距离越大，表示个体的分布密度越大，这些个体会以更大的概率进入到下一次优化迭代中，有利于维持解集的多样性。本文用每个目标函数上与其相邻的两个解距离差之和来计算个体xv的拥挤距离I（xv）：

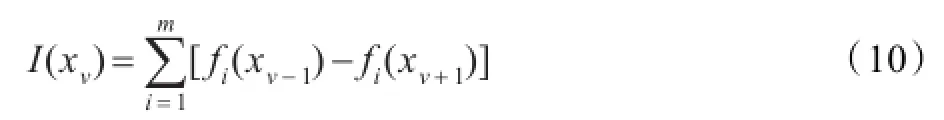
其中xv-1和xv+1为将解集按照第i个目标函数值升序排列后与xv相邻的两个解，对应排序在边缘上的个体x1和xk，赋予一个极大值，m表示目标函数的个数，fi表示第i个子目标。每一个体的拥挤度距离计算时间复杂度为O（mn），其中n为种群的规模。采用公式（10）的拥挤度距离计算公式，计算时间复杂度明显降低，使得到的解均匀分布在Pareto前言，增加了解集的多样性。

3.3非支配排序

对于待优化问题中的解，为了保持非支配解分布的均匀性和解的多样性，采用综合模糊适宜值FFM和拥挤距离的策略进行排序，具体步骤如下：

（1）对于每个栖息地，根据目标函数F1和F2，计算其对应的模糊适宜值FFM，FFM大的栖息地排在前面。

（2）如果FFM相同，则拥挤距离大的栖息地排在前面。

4　生物地理学算法

生物地理学优化算法（BBO）的基本思想是通过群体中相邻个体的迁移和特别个体的突变来寻找全局最优解。在BBO中，每个个体被认为是一个栖息地（habitat），如果某个栖息地非常适合生物居住，则该栖息地具有较高的适宜度指数（habitat suitability index，HSI），与HSI相关的影响因子被定义为适宜度指数变量（suitability index variables，SIV）。在车间作业调度问题中，选用待调度的设备、工人和未加工的任务作为决策变量，每个决策变量为各栖息地的SIV，由决策变量得到的目标函数为适宜度指数HSI。

4.1栖息地编码

根据离散制造车间作业调度的特点，将决策变量（待调度的设备、工人和未加工的任务）表示成适合BBO求解的码串形式。在实际作业调度中，不仅要确定工序的加工顺序，还需为每道工序选择一台合适的设备，并且为每个设备选择合适的工人，因此，其相应的编码由三部分组成。本文采用的编码方式如式（11）所示。

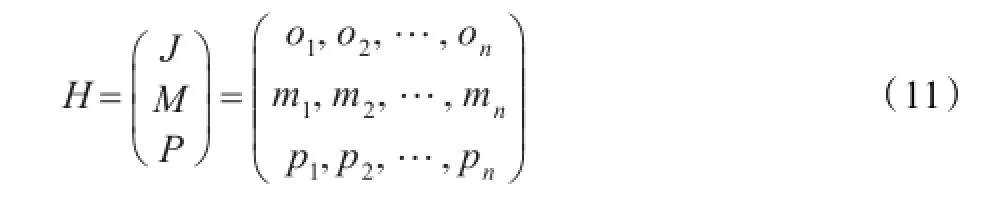
第一层编码J表示工序的编码，用相同的符号表示同一个零件的所有工序，根据这些符号在数组J中出现的次数确定是第几道工序。第二层编码M是该零件相应工序所使用的设备分配编码，可在该工序的可用设备集中选择。第三层编码P是可以操作该设备的工人编码，可在操作该设备的工人集中选择。这种编码方式的优点是可以满足工艺路线柔性化、设备和人员选择柔性化。将三层编码对应起来，可得到车间作业调度的一个可行解。表1表示一个编码示例，表中零件2的第一道工序在可用设备3上加工，由工人1操作该设备。该编码方式能够满足加工路线柔性化和加工资源不唯一的约束条件。

表1　CHPSO栖息地编码图

4.2栖息地初始化

在BBO算法中，设存在n个栖息地，每个栖息地表示车间调度的一个可行的调度方案。具体的初始化步骤是：

（1）令循环次数k=1。

（2）将第H（k）个栖息地编码的第一行置0。

（3）根据各零件i的工序数Ji，在栖息编码的第一行随机寻找Ji个未被占用的空位（0位），将i赋给选中的空位。

（4）从左到右，根据各零件i和工序号j，从可选的设备集Mij中随机选择一个设备，从可选的工人集P中随机选择一个工人，分别赋给H（k）的第二行和第三行（即设备编码和工人编码）。

（5）令k=k+1。

（6）若k≤n，转向（2），否则，退出循环。

4.3栖息地解码

解码过程就是根据栖息地的编码信息，确定每道工序在设备上的加工顺序及开始/结束时间，确定操作加工设备的工人，从而产生相应的调度方案。具体步骤是：

（1）根据栖息地中零件编号的相对位置，确定每个位置对应的工序编号，用Oij表示零件i的第j道工序，设备和工人状态均为空闲（即为0）。

（2）从左到右依次读取Oij，计算Oij的最早开始时间Sij。首先判断Oij是否为零件i的第一道工序，如果是第一道工序，Sij=Ti（Ti为零件释放时间），如果不是第一道工序，则是前一道工序的完工时间Sij=Ci（j-1）（Ci（j-1）为工序Oi（j-1）的完工时间）。

（3）获取加工Oij的设备m当前所有的空闲时间段（即设备状态为0的时间段），并将最早的空闲时段记为［Rm，Qm］。

（4）获取操作m的工人p当前所有的空闲时间段（即工人p状态为0的时间段），并将最早的空闲时段记为［Rp，Qp］。

（5）比较max（Sij，Rm，Rp）+Tijm与Qm和Qp，Tijm表示Oij在设备m上的加工时间，如果max（Sij，Rm，Rp）+ Tijm≤min（Qm，Qp），将Oij插入到设备和工人空闲时间段［max（Sij，Rm，Rp），max（Sij，Rm，Rp）+Tijm］中，并更新零件的结束时间、设备的开始时间和结束时间，工人的开始时间和结束时间。并将设备对应的工人状态置为1，工序oij加工完成后，将设备和工人的状态置为0，否则，转向（6）。

（6）令［Rm，Qm］和［Rp，Qp］为下一个可加工Oij的设备的时间段和工人的时间段，转向（5）。如果没有符合的空间时间段，则在该设备和工人加工序列的末尾安排Oij。

（7）当所有零件的全部工序安排到指定的设备和操作工人后，获得每个零件的完工时间，设备加工时间、读取单位时间内设备费用和可以操作设备的工人的单位工资成本，根据公式（1）和（2）分别计算总生产时间F1和加工成本F2。

4.4适应度函数计算

本文中适应度函数计算过程如下：

（1）将每个栖息地按照约束条件对其进行解码，根据公式（1）和公式（2）计算调度分目标函数值F1和F2。

（2）对于每个栖息地，根据计算的F1和F2，计算其对应的模糊适宜值FFM。

本文算法中模糊适宜值FFM计算的伪代码如图1所示。

4.5迁移

BBO算法通过迁移算子使各解之间进行信息共享，从而对求解空间进行广域搜索，进而更新栖息地得到更大更丰富的解集合。每个个体具有各自的迁入率λ和迁出率μ，文献［19］分析了6种线性和非线性物种迁移模型，本文选用符合自然规律的余弦迁移模型，从图2可以看出，当栖息地中有较少或较多物种时，λ和μ的变化比较平稳，而当栖息地种群数量达到平衡点时，λ和μ的变化比较快。余弦迁移模型计算如下：

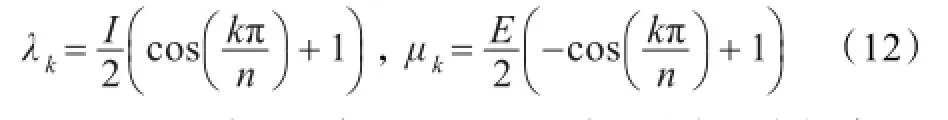
I表示最大迁入率，E表示最大迁出率，可将每个栖息地的HSI转换成物种数量来衡量其优劣。首先将栖息地按照其对应的HIS从大到小进行排序，并且设Smax=n，则Sr=Smax-r，r=1，2，…，n，r表示排序后的标号。将Si带入到公式（12）中，计算出栖息地Hr的迁入率λr和迁出率μr。

图1　模糊适宜值计算伪代码

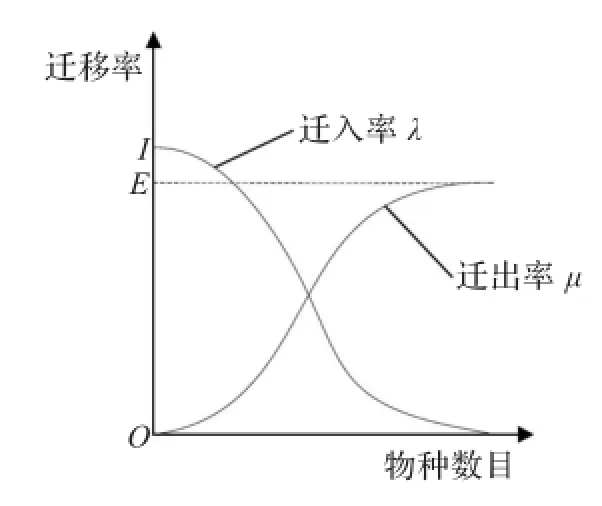
图2　余弦迁移模型

迁移操作的具体过程是：根据迁入率λr确定栖息地Hr是否发生迁移操作（栖息地的数量h作为循环次数）。随机产生（0，1）之间的随机数，如果小于λr，则Hr被确定发生迁入操作，那么利用其他栖息地的迁出率μ进行轮盘选择需迁出的栖息地Hq，然后按照迁移策略修改栖息地Hr。

当确定迁入栖息地Hi和迁出栖息地Hj以后，为保证栖息地可行性，结合栖息地的编码方案，本文采用的迁移策略的实现方式是：

（1）先将零件集｛n1，n2，…，nN｝随机划分为两个非空的集合G1和G2。

（2）将迁入栖息地Hi工序编码中属于G1的零件复制到临时栖息地Hk工序编码中，并保持它们的前后顺序和位置，同时将对应的设备和工人保持位置不动，复制到Hk设备编码和工人编码中。

（3）将迁出栖息地Hj中工序编码中包含G2的零件依次填到Hk中工序编码的空余位置，同时将对应的设备和工人保持位置不动，填到Hk设备编码和工人编码空余的位置。

迁移操作完成后，用Hk替换Hi。以3个零件，并且每个零件有4道加工工序为列，G1中包括零件1，G2中包含零件2和3，如图3所示。

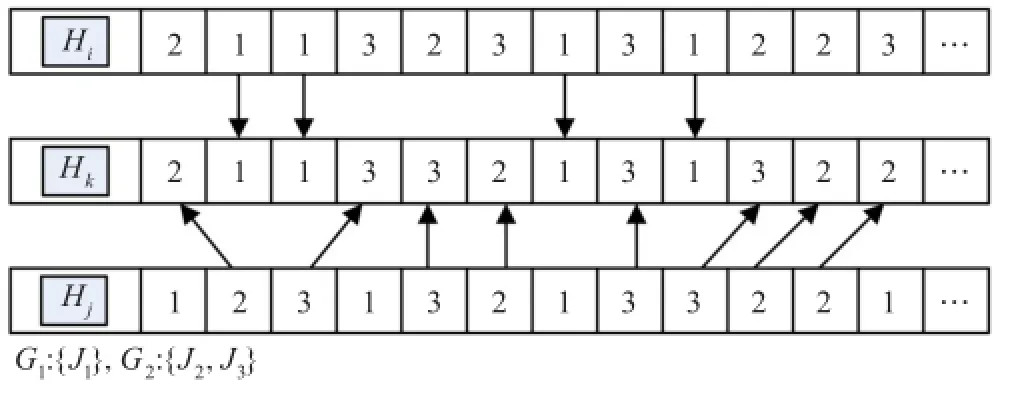
图3　迁移操作

4.6变异

其中，mmax为预定义的最大突变率，Pmax=max（Ps），s∈（1，2，…，n）。

在车间调度问题中，对于选择发生变异的栖息地（即调度方案），为保证变异后的个体是可行解，则按照以下策略进行变异。

（1）基于工序的变异：从种群中随机选取一个栖息地，在对应的栖息地第一行随机选取两个变异点，交换选取的两个变异点的位置，为保证变异的可行性，保存变异前的机床号和工人号。例如随机选取的栖息地如图4所示。

对其第一行的第二位和第六位交换位置，并保存对应的机器号和工序号，得到变异后栖息地如图5所示。

BBO算法的变异策略对算法是否会陷入局部最优和收敛精度均有较大影响。BBO变异操作是通过栖息地容纳物种数量的概率来对栖息地的特征变量进行突变，设栖息地恰好包含物种数S的概率为Ps，变异率为：

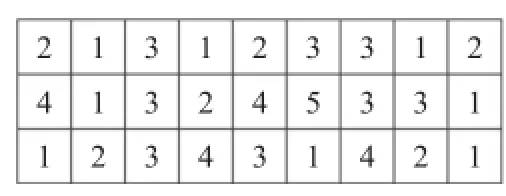
图4　变异前栖息地

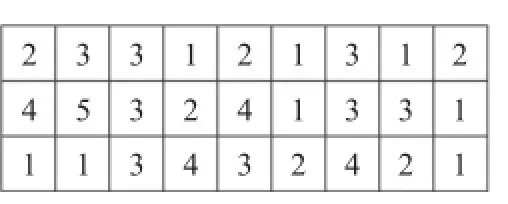
图5　变异后栖息地

（2）基于设备的变异：在基于设备的编码部分，随机选择两个位置上的设备编号，然后在其对应位置上的工序可用设备集合中获取加工时间最小的设备，如果与现使用的设备不同，则使用被选中的设备加工这道工序，否则，采用原来的加工设备。例如对于图5中的栖息地，假设工序o21可以在机器1、2和4上加工，采用机器2加工时间最小，则将栖息地的第二行第一位变为2，变异后的栖息地如图6所示。

（3）基于工人的变异：在基于工人的编码部分，随机选择某个位置上的工人编号，然后从设备可用的工人集中随机获取工人号，如果与其现在的操作工人不同，则替换原来的操作工人操作其对应的设备。例如对于图5中的栖息地，工序o31在机器3加工，假设机器3可由工人1、2和3操作，则随机从工人集中选取工人号代替当前工人3，变异后的栖息地如图7所示。

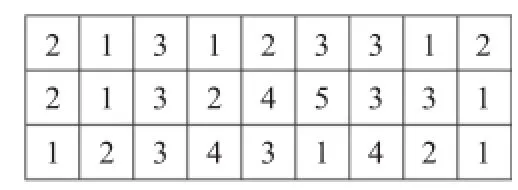
图6　基于设备的变异

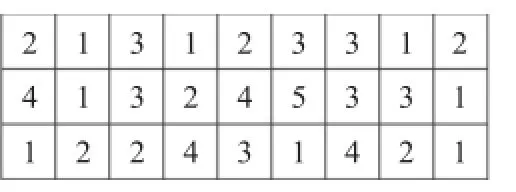
图7　基于工人的变异

4.7FPDCBBO算法

基于模糊Pareto支配的生物地理学算法（Fuzzy Pareto Dominance-CombinedBiogeography-BasedOptimization Scheduling Algorithm，FPDCBBO）基本思想是：在生物地理学算法（BBO）的基础上，用模糊适宜值和拥挤距离对解进行排序，代替基本的BBO算法中栖息地适宜度指数（HIV）作为解的评价标准。在算法迭代过程中，不用迁移和变异后的个体代替原有的个体，而是将产生的进化解集合与排序后的原解集融合，重新排序，选择排序靠前的解作为下一代解集，保证解集的多样性。

在离散制造车间作业调度问题中，待调度的设备、工人和未加工的任务作为栖息地中的决策变量，每个栖息地对应一个可行的调度方案，将FPDCBBO应用与车间作业调度的具体实现步骤为：

步骤1输入计算所需的原始数据，包括车间作业调度模型中的零件数量，每个零件对应的工序、设备参数、工人参数、约束参数等。设置BBO算法参数，设定栖息地数量n，栖息地最大物种数量Smax=L，迁入率函数最大值I，迁出率最大值E，全局迁移率Pmod。

步骤2初始化栖息地的SIV，这里的SIV指的是车间作业调度系统中的设备、工人和待加工的任务。对SIV进行编码，产生规模为n的初始栖息地SIV。

步骤3按照约束条件对栖息地进行解码，根据目标函数F1和F2计算调度分目标函数值。

步骤4非支配排序，对于每个栖息地，根据步骤3中的F1和F2，计算其对应的模糊适宜值FFM，FFM大的栖息地排在前面。如果FFM相同，则拥挤距离大的栖息地排在前面。则产生排序后的群栖息地n1。

步骤5将排序后的栖息序号映射为物种数量，来衡量栖息地所对应的车间解决方案的优劣。设栖息地最大物种数量Smax=L，则Sr=Smax-r，r=1，2，…，n，r表示排序后的标号。根据每个栖息地的物种数量，利用公式（12）计算其对应的迁入率和迁出率。

步骤6根据步骤5计算出的迁入率、迁出率和变异概率，对栖息地中的工序编码、设备编码和工人编码进行迁移和变异操作，产生进化群栖息地n2。

步骤7融合群栖息地n1和n2，形成数量为2n的群栖地w。

步骤8计算w中栖息地个体对应的分目标函数值，然后按照步骤4进行非支配排序。

步骤9选择前n个栖息地构成新一代群栖息地n3。

步骤10判断是否达到最大迭代次数，如果是，则结束运算，输出结果，否则迭代次数加1，转向步骤3。

对于步骤4中模糊Pareto实现的伪代码如图8所示。

图8　模糊Pareto实现伪代码

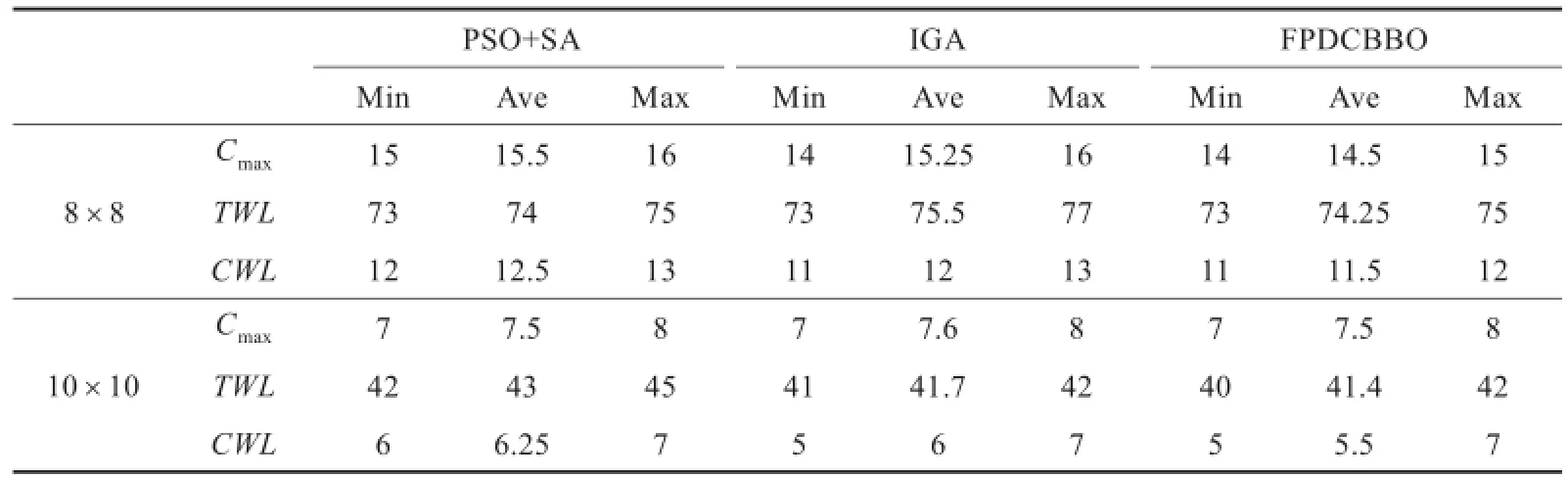
表2　不同规模测试问题结果比较

5　实例仿真

5.1基准测试仿真

为验证本文算法的有效性，以完工时间、所有机器总负荷、最大机器负荷为目标，使用文献［20］中8×8和10×10的柔性作业车间实例问题进行测试，并同已有的PSO+SA［21］，IGA［22］算法进行对比和分析，结果如表2所示，Cmax表示加工时间，TWL表示所有机器总负荷，CWL表示最大机器负荷。从表中可知，对于三个性能指标，本文算法在这些问题上的求解平均值优于其他算法得到的结果。

5.2实例仿真

以某离散模具车间为例，该车间拥有数控车床、普通车床、摇臂钻床、万向摇臂钻床、电火花、铣床6台多功能设备（M1～M6），每个设备可以加工不同的工序。在一个生产周期内，需要为一套注塑模具加工不同的6种模具零件（N1～N6），每个零件有4道加工工序（O1～O4），有4个工人（P1～P4）操作这6台设备。具体描述信息如表3，表4，表5，表6。

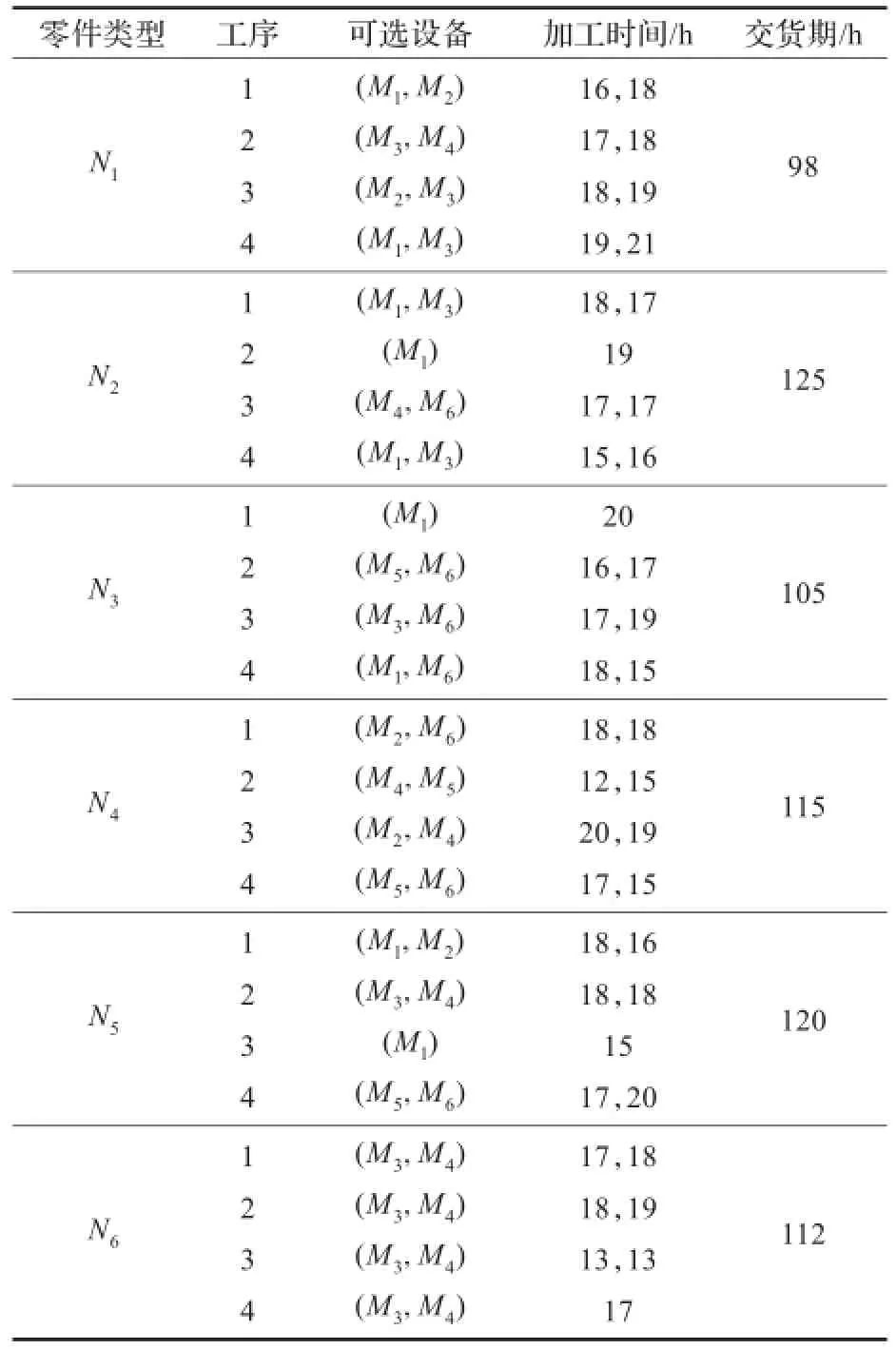
表3　制造单元信息

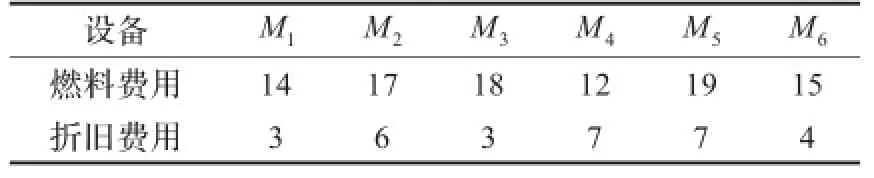
表4　设备费用（元·h-1）

表5　工人费用（元·h-1）

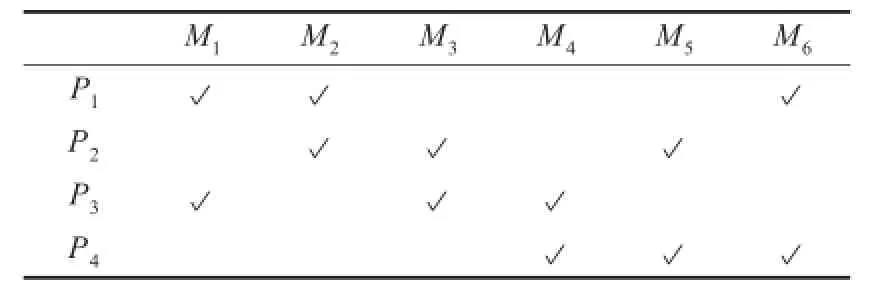
表6　工人与设备的关系

以本文所建立作业调度数学模型中的加工周期最小和生产成本最小目标为优化目标，将本文提出的算法应用于上述实例，设置算法参数：栖息地数量n=100，最大变异率mmax=0.05，最大迁入概率和最大迁出概率I=E=1.0，迭代次数为150，独立运行20次，得到完工时间最小为121时，面向设备的调度甘特图如图9所示，面向工人的调度甘特图如图10所示，时间-成本关系如图11所示。

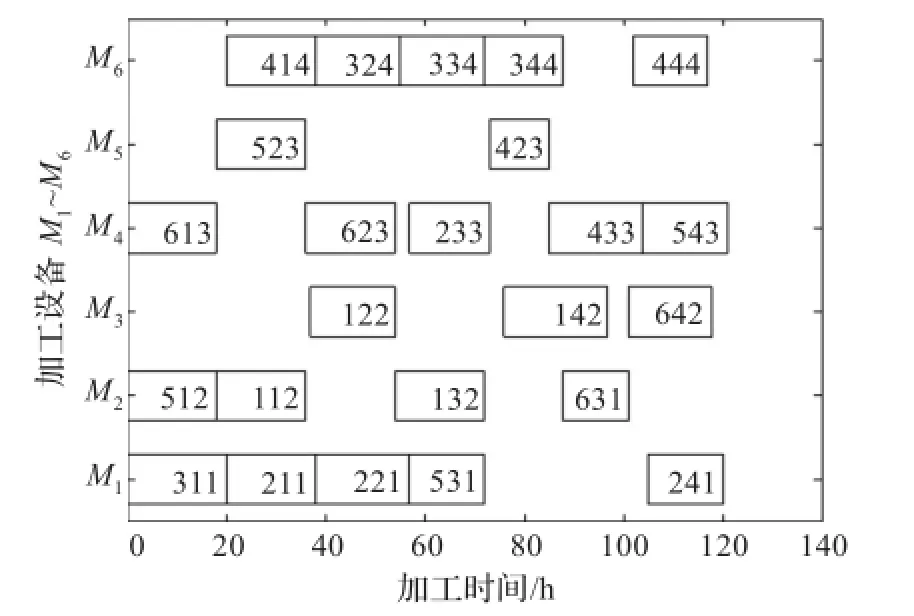
图9　面向设备的调度甘特图

图10　面向工人的调度甘特图

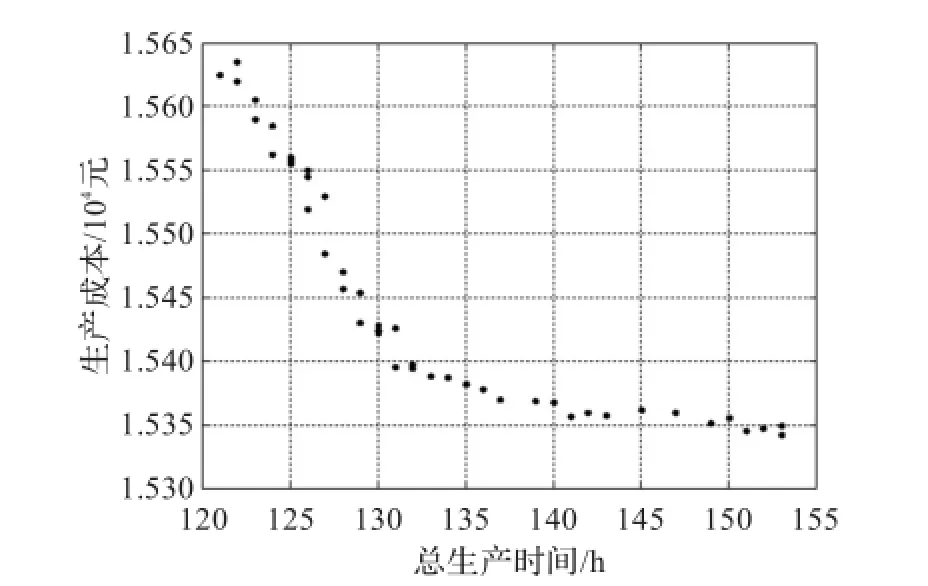
图11　FPDCBBO生产时间-成本关系图

在图9中，方块中的第一个数为零件号，第二个数为零件对应工序号，第三个数为操作该设备的工人号。如第一行中的‘311’表示第3个零件的第1道工序在设备1上加工，由工人1操作。在图10中，方块中的第一个数为零件号，第二个数为零件对应工序号，第三个数为该工人操作的设备号。如第二行中的‘513’表示第5个零件的第1道工序在设备3上加工，在由工人2操作。从甘特图的结果可以看出，设备和工人双资源的利用率比较均衡，加工零件可按时完成。

为了验证本文提出的调度算法在求解人机双资源约束的作业调度上的优越性，与NSGA-II算法进行对比分析，算法的种群规模和最大迭代次数与FPDCBOO算法相同，得到的时间-成本关系如图12所示。

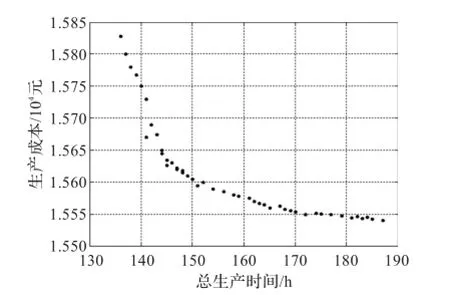
图12　NSGA-II生产时间-成本关系图

由图12可以看出，NSGA-II算法输出的生产时间-成本关系图中解集分布在生产总流程时间区间（130，190）与成本区间（15 500，15 850）的交集中，由图11可以看出，本文FPDCBBO算法输出的生产时间-成本关系图中，解集分布在生产总流程时间区间（120，155）与成本区间（15 300，15 650）的交集中，即本文算法缩短了生产总流程时间。此外，相比NSGA-II算法，本文算法产生的Pareto均匀性较好。表7中对于完工时间最小化和总加工成本最小化目标，本文算法得到的最优值及平均值均优于NSGA-II算法，更适合求解多目标柔性车间调度问题。

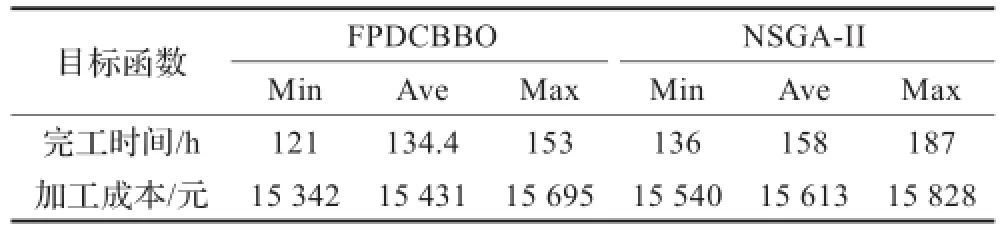
表7　算法结果的对比

6　结束语

本文基于制造车间的生产特点建立了以设备和工人双资源约束的，以最小化加工时间和最小化加工成本为目标的车间调度模型，提出了一种采用基于模糊Pareto支配的生物地理学算法，在BBO算法中，决策变量采用三层编码方法，既解决了工序调度问题，又解决了设备和人员分配的问题，采用余弦迁移模型提高生物地理学算法的收敛速度。采用综合模糊Pareto支配和分布密度的Pareto解集排序方法，促进Pareto最优前沿向理想Pareto前沿逼近，并保持了Pareto解集的多样性。通过模拟某制造车间的实际数据对本文算法进行了仿真，结果验证了调度模型的合理性和调度算法的有效性。

［1］王万良，吴启迪.生产调度智能算法及其应用［M］.北京：科学出版社，2007：12-13.

［2］Xing L，Chen Y，Yang K.Multi-objective flexible Job Shop scheduling：design and evaluation by simulation modeling［J］. Applied Soft Computing，2009，9（1）：362-376.

［3］徐新黎，应时彦，王万良.求解模糊柔性Job shop调度问题的多智能体免疫算法［J］.控制与决策，2010，25（2）：171-184.

［4］Zhang G，Gao L，Shi Y.A genetic algorithm and tabu search for multi objective flexible job shop scheduling problems［C］// 2010 International Conference on Computing，Control and Industrial Engineering（CCIE），2010，4：250-254.

［5］刘爱军，杨育，程文明，等.复杂制造环境下的改进非支配排序遗传算法［J］.计算机集成制造系统，2012，18（11）：2446-2458.

［6］李鹏，邱顺流，宋豫川，等.基于瓶颈工序的多资源多目标机械加工车间调度研究［J］.现代制造工程，2013，1（1）：1-6.

［7］Peteghem V，Vanhoucke M.A genetic algorithm for the preemptive and non-preemptive multi-mode resource-constrained project scheduling problem［J］.European Journal of Operational Research，2010，201（2）：409-418.

［8］袁亮，袁逸萍，孙文磊，等.双资源柔性车间多目标调度优化研究［J］.组合机床与自动化加工技术，2013（12）：149-152.

［9］Sha D Y，Lin H H.A multi-objective PSO for job shop scheduling problems［C］//Proceedings of theInternational Conference on Computer and Industrial Engineering.Troyes，2009：489-494.

［10］宋存利.求解柔性作业调度问题的协同进化粒子群算法［J］.计算机工程与应用，2013，49（21）：15-18.

［11］Sun B，Wang H，Fang Y.Application of ant colony algorithm in discrete job shop scheduling［C］//Proceedings of the 2nd International Symposium on Knowledge Acquisition and Modeling（KAM），Wuhan，2009：29-31.

［12］王硕.基于改进蚁群算法的作业车间调度研究［D］.上海：华东理工大学，2013.

［13］Simon D.Biogeography-based optimization［J］.IEEE Transactions Evolutionary Computation，2008，6（12）：702-713.

［14］Panchal V K，Singh P，Kaur N.Biogeography based satellite image classification［J］.International Journal of Computer Science and Information Security，2009，6（2）：269-274.

［15］Savsani V，Rao R，Vakharia D.Discrete optimization of a gear train using biogeography based optimization technique［J］.InternationalJournalofDesignEngineering，2009，2（2）：205-223.

［16］陈道君，龚庆武，乔卉，等.采用改进生物地理学算法的风电并网电力系统多目标发电调度［J］.中国电机工程学报，2012，32（31）：150-158.［17］Rahmati S H A，Zandieh M.A new biogeography-based optimization algorithm for the flexible job shop scheduling problem［J］.International Journal of Advanced Manufacturing Technology，2012，58（9）：1115-1129.

［18］He Z，Yen G G，Zhang J.Fuzzy-based Pareto optimality many-objective evolutionary algorithms［J］.IEEE Transactions on Evolutionary Computation，2013，99（1）：1-15.

［19］Ma H.An analysis of the equilibrium of migration models for biogeography-based optimization［J］.Information Sciences，2010，180（18）：3444-3464.

［20］Kacem I，Hammadi S，Borne P.Approach by localization and multi-objective evolutionary optimization for flexible job-shop scheduling problems［J］.IEEE Transactions on Systems，Man and Cybernetics，2002，32（1）：408-419.

［21］Xia W J，Wu Z M.An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problem［J］.Computers&Industrial Engineering，2005，48：409-425.

［22］周晏明.基于改进遗传算法的多目标作业车间调度研究［D］.哈尔滨：东北林业大学，2013.

Biogeography-based optimization algorithm for flexible job-shop scheduling problems.

WU Dinghui，KONG Fei，ZHU Shaowen，JI Zhicheng

Key Laboratory of Advanced Process Control for Light Industry，Jiangnan University，Wuxi，Jiangsu 214122，China

To solve the multi-objective problem in flexible job-shop scheduling considering the resource constraints of machines and operators，Fuzzy Pareto Dominance-Combined Biogeography-Based Optimization scheduling algorithm（FPDCBBO）is proposed.Using the method of fuzzy Pareto to calculate the dominant degree between the solutions and sorted，updating the global optimal value.Cosine migration model is used to improve the convergence speed of biogeography-based algorithm.Finally，the algorithm is applied in an actual production instances，the feasibility and efficiency of algorithm are verified.

flexible job-shop scheduling；Fuzzy Pareto Dominance（FPD）；Biogeography-Based Optimization algorithm（BBO）；cosine migration model；double resource constraints

A

TP393

10.3778/j.issn.1002-8331.1408-0178

国家高技术研究发展计划（No.2013AA040405）。

吴定会（1970—），男，博士，副教授，研究领域为RFID网络优化，生产调度；孔飞（1986—），男，硕士研究生，研究领域为车间作业调度；朱绍文（1988—），女，硕士，研究领域为生产作业调度；纪志成（1961—），男，博士，教授，研究领域为运动控制、RFID网络优化。E-mail：wh033098@163.com

2014-08-28

2014-11-25

1002-8331（2015）22-0206-08

CNKI网络优先出版：2015-04-01，http://www.cnki.net/kcms/detail/11.2127.TP.20150401.1639.014.html