基于改进PSO的装备维修器材调剂供应决策

于双双，王铁宁，可荣博，李宁

1.装甲兵工程学院技术保障工程系，北京100072

2.中国人民解放军61377部队

3.中国人民解放军78416部队

基于改进PSO的装备维修器材调剂供应决策

于双双1，王铁宁1，可荣博2，李宁3

1.装甲兵工程学院技术保障工程系，北京100072

2.中国人民解放军61377部队

3.中国人民解放军78416部队

分析了装备维修器材存储保障存在的问题，提出采用调剂供应缓解存储保障的资源失衡问题，充分利用存储过剩的超储器材补充库存短缺的需求单位，建立了装备维修器材调剂供应的多目标决策模型，采用ε-约束法对模型进行处理，基于引导因子设计了改进的粒子群优化算法（Particle Swarm Optimization，PSO）对模型求解，并通过仿真实例进行了验证。结果表明，采用调剂供应的方式，可使保障系统内的资源存储得到有效的平衡，装备维修器材的保障效率也有所提高。

装备维修器材；调剂供应；决策；改进粒子群优化算法

1　引言

器材存储是器材保障中必不可少的环节，合理的器材储备可以提高资源点的保障能力［1］。然而，根据装备维修器材业务数据统计，目前我军装备维修器材保障资源存储失衡问题较为严重，一方面，大量器材长期处于“呆滞”状态，存储量远高于储备定额，不仅造成器材资源和存储空间的浪费，同时也耗费了大量的维护和保养成本［2］，称其为“超储器材”；另一方面，部分种类器材缺货较为严重，不能满足本年度的维修任务，导致保障成本和保障时间的增加，称其为“欠储器材”。资源存储失衡问题严重影响了器材的保障效率。如果在组织年度申请计划筹措之前，利用超储的资源点对器材欠储单位进行一轮器材补充，一方面节约器材采购成本，另一方面平衡资源结构，称此过程为器材的调剂供应。虽然已有学者对装备保障资源的优化配置问题［3-8］与资源调度问题［9-12］进行了一些研究，提出了一些库存优化管理的方法与模型［13-17］，但针对同级保障节点之间的库存的过剩与短缺之间的调剂问题还没有针对性的研究。此外，现有装备资源调度问题的研究大多是在纵向供应保障模式的前提下进行的，考虑逐级或越级供应，对于同级保障节点间的器材协调供应问题没有展开研究。

针对装备维修器材保障体系的资源存储失衡现状，本文认为，在装备维修器材保障过程中，通过合理运用调剂供应，不区分保障单位的级别，充分利用“存储过剩”的器材资源补充“库存短缺”的器材需求单位，可以使当前保障体系存在的资源存储失衡问题得到有效缓解，也可有效节约器材采购成本。将调剂供应问题分为两种情况：一种是保障区域内仅有一个资源点处于欠储状态，另一种是多个资源点处于欠储状态，本文重点对第二种情况进行研究，对保障区域内的资源进行整体的优化与平衡。

2　装备维修器材调剂供应问题分析

调剂供应的主要目标是通过组织器材超储资源点与欠储资源点之间的调剂，优化当前系统中器材资源存储的不平衡状态，使得资源调整后的保障系统保障效率更高。与其他普通资源调度问题相比，本文研究的调剂供应问题最大的不同就是首先要对各个资源点的库存情况进行详细分析，对其超储、欠储的状态、程度、数量等进行定性、定量判定，然后基于超欠储情况才能进行后续的器材的协调分配，两部分内容均有一定的难度。此外，本文调剂供应问题中器材的协调分配可在同级保障节点间展开，而其他普通资源调度问题要严格按照保障级别逐级或者越级展开。

文献［2］指出了超储、欠储的状态、数量及程度的判定方法，本文以此为基础，对全军资源点进行分析，以欠储状态作为资源点存在缺货风险的判断标准，以欠储数量作为需要进行调剂的数量参考，以欠储程度作为资源点对调剂的迫切程度研究装备维修器材的调剂供应决策问题。

O｛O1，O2，…，Om｝为保障体系内所有超储资源点的集合，U｛U1，U2，…，Un｝为所有欠储资源点的集合，各资源点的超储、欠储情况已知；S｛S1，S2，…，Sl｝为其他所有正常状态资源点的集合，所有资源点的库存数量及预测需求已知；资源点之间的运输路线已知。制定调剂方案，优化装备维修器材保障体系，提高器材的利用率、节约保障成本、提高保障效率。

3　装备维修器材调剂供应决策模型

3.1目标函数的确定

装备维修器材调剂供应的主要目标是在下一个供应周期之前提高装备维修器材的保障效率，保障效率主要体现在保障成本、保障时间、器材利用率三个方面。

（1）保障成本目标

从本次调剂之后到下一个供应周期之前这段时间所产生的保障总成本包括调剂成本、采购成本、运输成本、存储成本4个部分。

①调剂成本

装备维修器材调剂供应的物流方向是从超储资源点向需求点。设由超储资源点Oi向欠储资源点Uj调剂的数量为SRij，调剂后资源点的库存为：

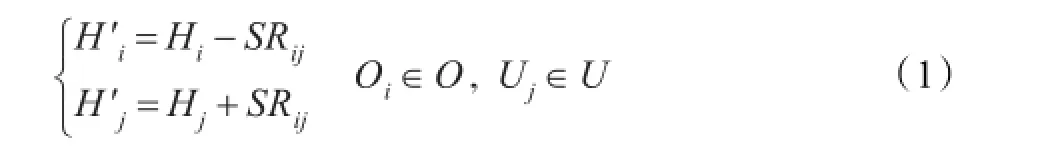
式中Hi为Oi的当前库存；Hj为Uj的当前库存。

设由超储资源点Oi向正常状态资源点Sk调剂的数量为SRik，调剂后资源点的库存为：

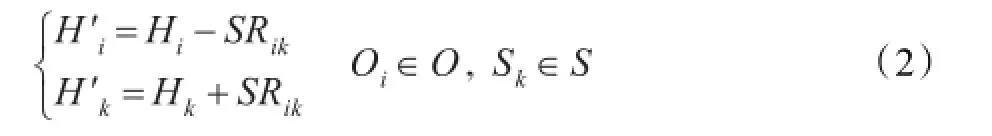
式中Hk为Sk的当前库存。

所有调剂结束后，各资源点的库存为：

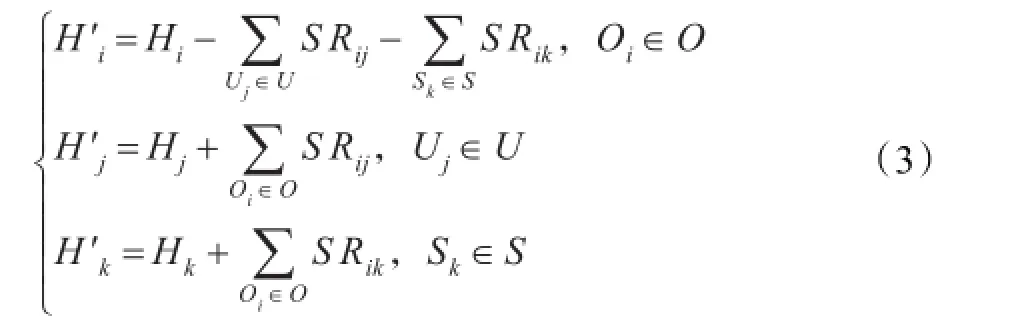
调剂过程所产生的成本TCR主要包括运输成本和调剂准备成本两个部分，即

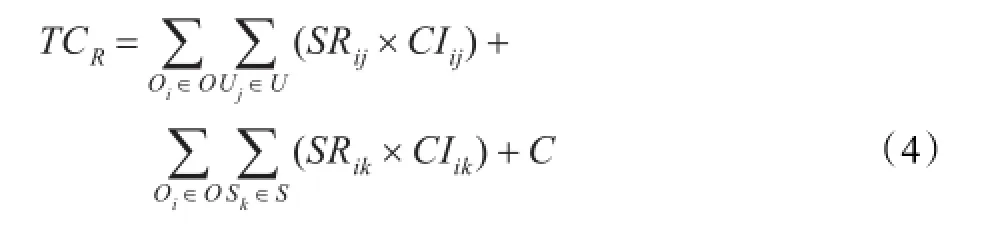
式中CIij为单位器材从资源点i到j的运输成本；CIik为单位器材从i到k的运输成本；C为调剂准备成本。

②采购成本

器材的累积采购成本为：

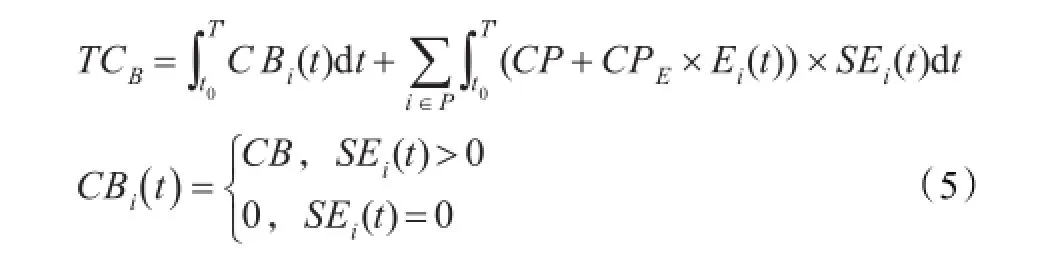
式中CBi（t）为t时刻向资源点i的固定订货成本；SEi（t）为i在t时刻的工厂订货数量；CB为工厂订货的固定成本（元/次）；CP为器材单价；CPE为紧急订货的单位器材附加成本；Ei（t）为订货是否为紧急订货的参数，如果是，则Ei（t）=1，否则Ei（t）=0；t0为当前时刻；T ′为从t0开始的下一个集中供应时刻；P为所有资源点的集合，P=｛O，U，S｝。

③运输成本

器材的累积运输成本为：

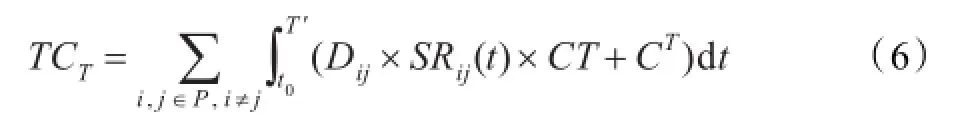
式中Dij为从资源点i到j的距离；SRij（t）为t时刻从i到j的器材供应数量；CT为单位器材的单位运输成本。

④存储成本

器材的累积存储成本为：

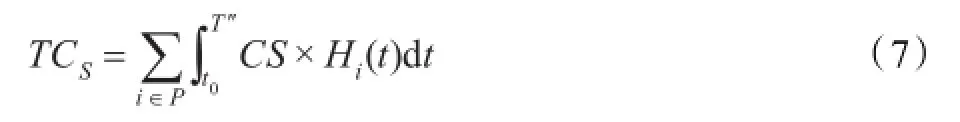
式中CS为器材的单位存储价格（元/天·件）；Hi（t）为t时刻资源点i的库存数量。

⑤保障成本目标

由于保障总成本的计算方法是累加从当前时刻到下一次集中订货前所产生的总成本，受起始时间的影响，本文以平均保障成本最低作为保障成本的目标。保障成本的目标函数为：

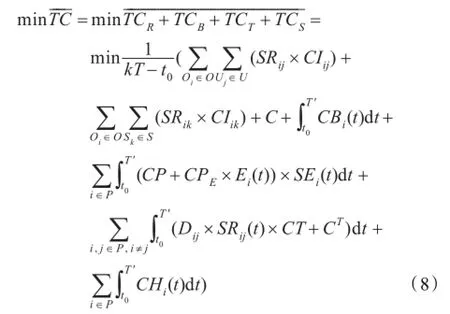
（2）保障时间目标

采用维修器材的平均保障时间作为衡量保障时间的指标。保障时间总量（单位：天/件）可由未满足需求量（单位：件）与时间所围成的柱状面积表示，则保障时间总量为：

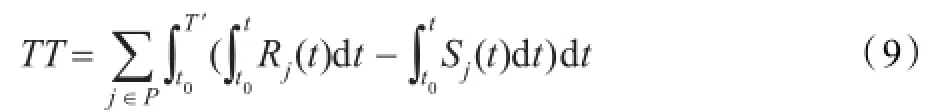
式中Rj（t）为t时刻需求点j的需求数量；Sj（t）为t时刻供应到达需求点j的器材数量。

模型以缩短保障时间为目标，同上分析，保障时间的目标函数为：

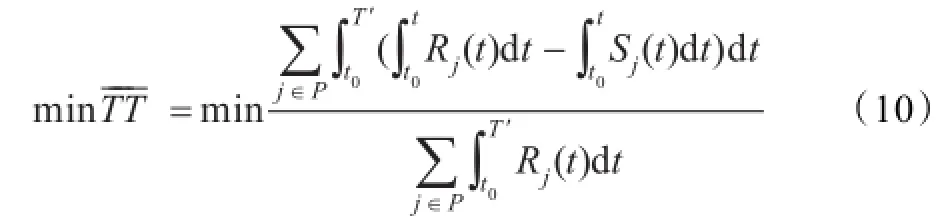
（3）器材利用率目标

器材的利用率亦器材周转率，即T时间内的器材消耗量与总库存量的比值。模型以提高器材利用率为目标，器材利用率的目标函数为：

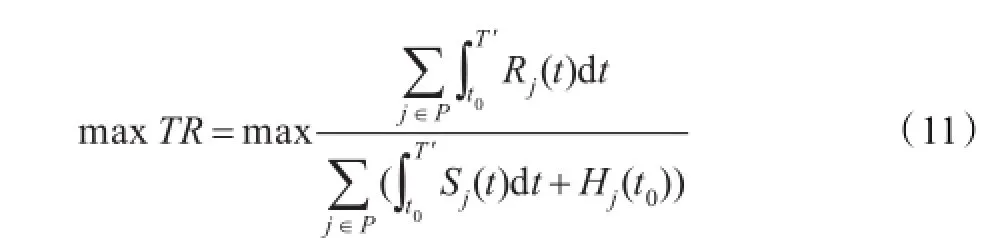
式中Hj（t0）为资源点j在t0时刻的库存量。

3.2约束条件的确定

模型的约束条件包括供应点约束、超储数量约束、供应数量约束3个方面。

（1）供应点的约束。只允许超储资源点向欠储资源点或正常状态资源点进行调剂，且调剂数量为非负整数，即

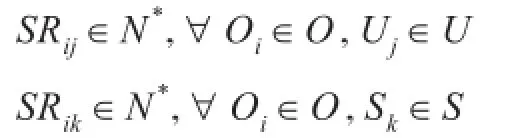
（2）超储数量的约束。任意超储资源点调剂供应数量不能超过该资源的超储数量，即

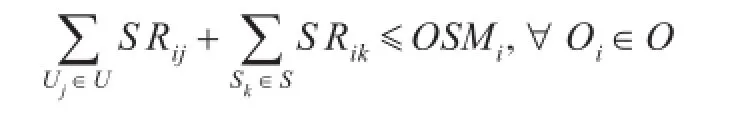
式中OSMi为Oi的超储数量。

（3）供应数量的约束。需求点获得调剂的器材后，其状态不能变为超储，即

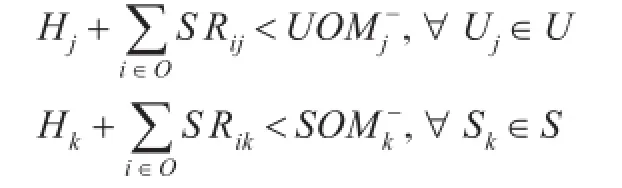
4　基于改进粒子群优化算法的模型求解算法设计

4.1模型的简化

模型包含保障成本、保障时间、器材利用率3个方面的目标，属于多目标优化问题。为简化模型求解，对模型目标进行简化处理。

（1）保障时间目标

ε-约束法是多目标优化方法中常用方法之一。ε-约束法从多目标中选择一个目标作为主目标，而将其他目标转化约束。

保障时间是体现保障能力的重要指标。如果维修所需的器材不能第一时间获得，会直接影响装备的完好率。如果平均保障时间为0，说明所有的需求通过本级资源点直接供应就可以满足，保障率为100%。然而，要使保障率达到100%，需要各级资源点牺牲库存成本为代价，存储大量器材以应对需求的随机性。为保证系统的保障能力，要求调剂优化后保障系统的保障率达到98%以上，在此基础上考虑保障成本等其他目标，则保障时间目标可以通过ε-约束法化简为约束条件。

保障时间总量与保障率的关系为：

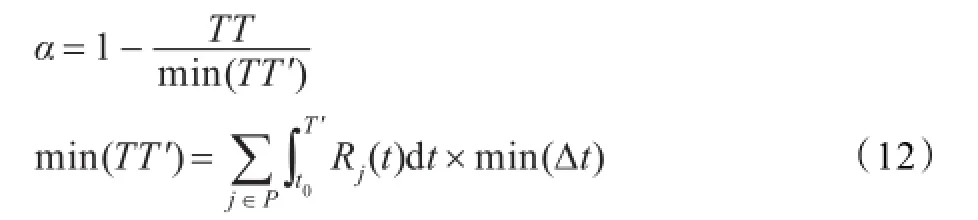
式中α为保障率；TT为实际的保障时间总量；min（TT′）为理论上的保障总时间最小上限。

要使α＞98%，结合式（9）、（10），则保障时间目标转化为约束条件，即

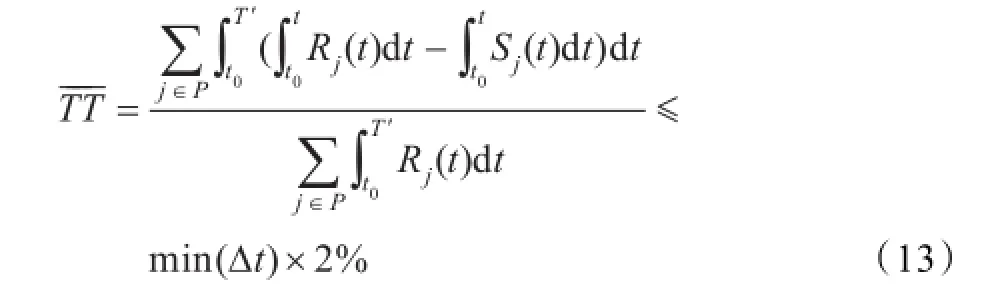
（2）器材利用率目标

器材的利用率只是器材保障效率的一种表象，器材的利用率低，表明保障过程中器材周转较慢，部分器材处于闲置状态，不仅造成空间存储资源的浪费以及人员管理成本的增加，同时也会影响器材的使用性能。这两方面均与器材的存储量和存储时间相关，为简化目标函数，将其并入存储成本的计算中，式（7）变为：

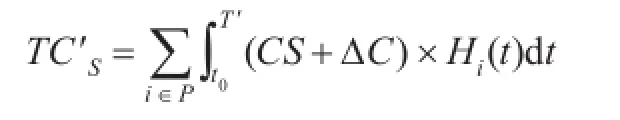
式中ΔC为单位器材在单位时间所消耗的空间存储资源、人员管理成本以及器材性能降低的代价。

综上，简化后的装备维修器材调剂供应决策模型为

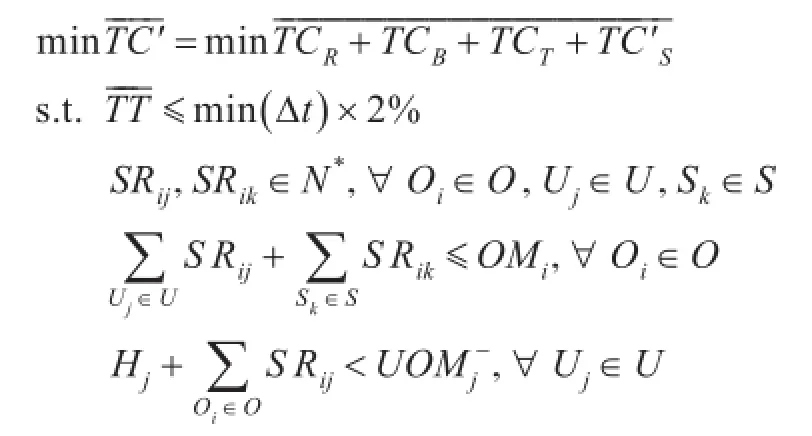
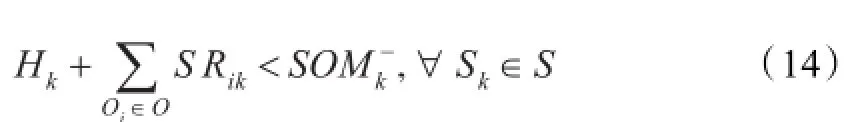
4.2基于粒子群优化算法的模型仿真求解思路

调剂供应决策模型的实质是针对当前保障系统的资源点超储/欠储情况，组织额外的器材调剂，即除逐级供应、越级供应外，在同级保障节点间快速实施资源的协调分配以优化保障系统的器材资源存储平衡状态，提高保障效率。分析式（14），只有TCR部分可以通过当前保障方案求得，而TCB、TCT、TC′S都是描述调剂后的保障产生的代价，传统的数学解析方法和智能搜索算法无法对调剂后的保障过程进行描述，因此无法对该模型进行求解。

粒子群优化算法（Particle Swarm Optimization，PSO）属于进化算法的一种，PSO算法的运行机理是对生物群体的社会行为进行模拟，它最早源于对鸟群觅食行为的研究［18-19］。它和遗传算法相似，也是从随机解出发通过迭代寻找最优解，通过适应度来评价解的品质，但它比遗传算法更为简单，它没有遗传算法的“交叉”和“变异”过程，但是每个“粒子”具有记忆，它通过追随当前搜索到的最优值来寻找全局最优［20-21］。本文将采用基于粒子群优化算法的仿真方法求解调剂供应决策模型，总体思路如图1所示。

（1）针对当前保障系统建立仿真系统模型。

（2）根据当前保障体系内资源点超储/欠储情况，提出初始的调剂供应方案（相当于初始粒子）。

（3）以一年为一个仿真周期，在每一轮仿真开始时，首先根据调剂供应方案执行一轮调剂供应，接下来继续仿真调剂供应后的保障过程。

（4）每轮仿真结束后，对仿真过程中的保障成本和保障时间等信息进行统计，求得本轮仿真的适应值（目标函数值）。

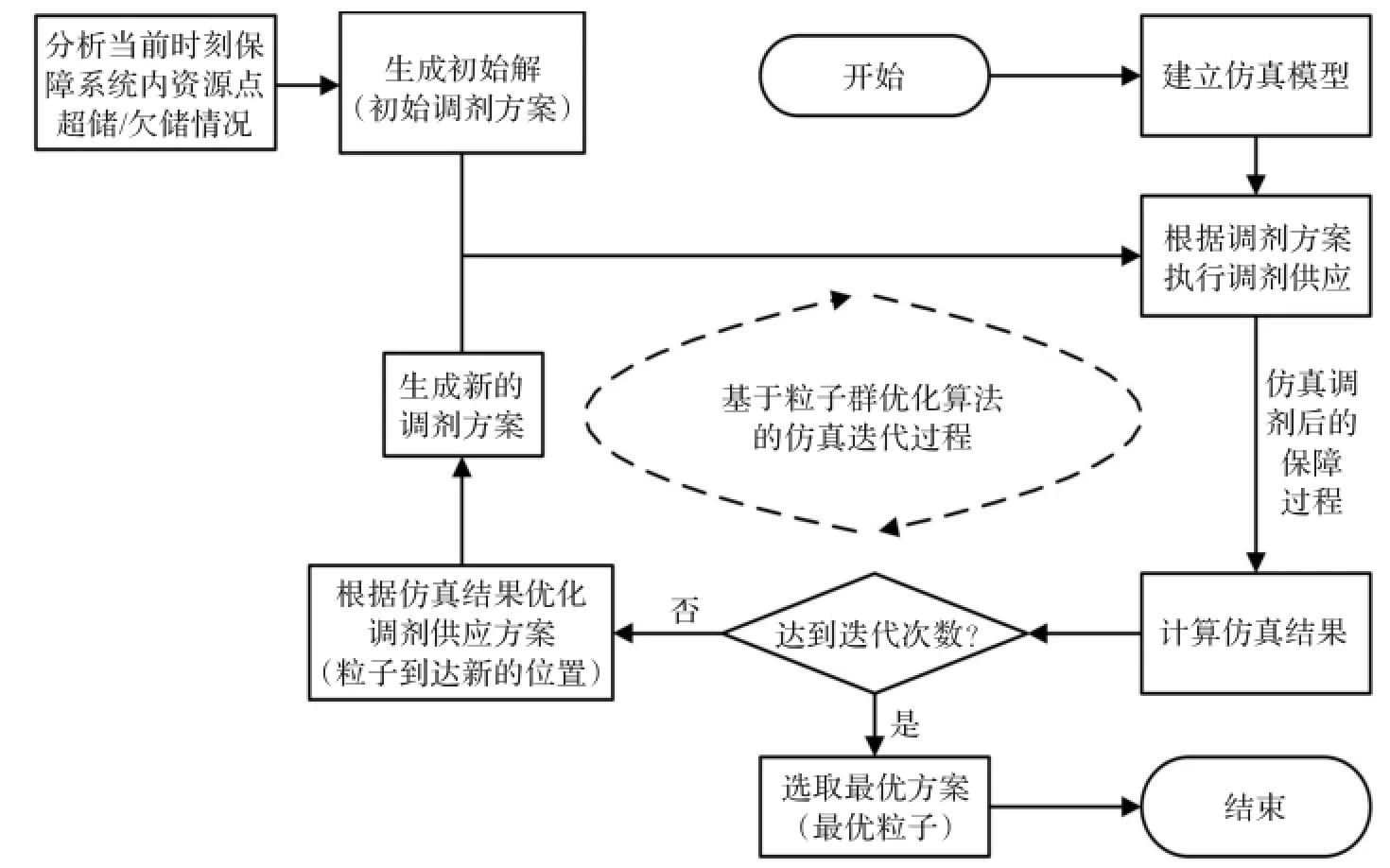
图1　基于粒子群优化算法的调剂供应决策模型求解思路

（5）如果没有达到迭代次数，则通过改进PSO算法，根据适应值调整调剂供应的决策方案（得到粒子的新位置），转入（3），进入下一轮迭代仿真。

（6）当达到迭代次数后，仿真结束，选取适应值最高的一轮仿真中的调剂供应方案作为最优方案。4.3改进粒子群优化算法设计

4.3.1PSO的基本原理与步骤

在PSO中，每个个体叫做“粒子”，每次迭代中，所有粒子在D维空间“移动”以搜索全局最优解。第i个粒子在第t次迭代中的位置为］，速度为。根据粒子的位置向量可以计算当前的适应值，作为衡量粒子优劣的标准。通过评价粒子的适应度，可得第t次迭代粒子i的个体最优位置，以及粒子的邻居搜索到的最优位置。在迭代过程中，粒子的搜索算法为：

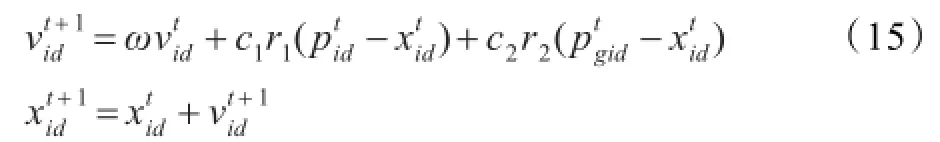
式中r1，r2为均匀分布在［0，1］区间的随机数；c1，c2为加速系数，c1控制粒子向自身个体最好位置方向移动的步长，c2控制粒子向位置最好的邻居方向移动的步长；d=1，2，…，D；ω为惯性权重，一般取值为0.9～0.4；i=1，2，…，Ng，Ng为种群的规模。

PSO的主要步骤如下：

（1）初始化参数和种群。设置位置上下限、速度上下限、最大迭代次数、粒子的维数、群体规模和加速系数、惯性权重等参数。确定初始种群的粒子位置和速度，t=0。

（5）如果达到迭代次数或满足终止条件，则输出最优解；否则，t=t+1，转入（3），进行下一次迭代。

4.3.2基于引导因子的改进粒子群优化算法设计

由于粒子的学习过程总是根据个体最优位置和邻居的最优位置进行更新，算法的收敛速度很快，但粒子的运动方向比较依赖于种群的总体趋势，难于发现和探索新的位置，如果初始种群的质量较低，则搜索容易陷入局部最优。

由于调剂决策目标的特殊性，本文采用基于PSO的仿真优化方法，每一个粒子代表一个调剂供应方案，粒子的适应值需要通过仿真调剂后的保障过程经统计得出。在每次仿真结束后，通过分析每个资源点的超储/欠储状态，可以对调剂方案的合理性进行反馈，并对调剂方案的调整进行引导，即对算法中的每个粒子进行引导。针对调剂模型的特点，基于引导因子对粒子群的搜索算法进行如下改进

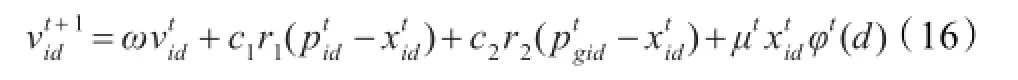
（1）φt（d）的确定

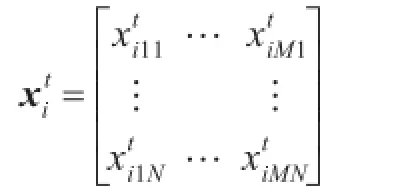
根据模型约定的调剂原则，由超储资源点向非超储资源点进行调剂，如果保障体系中共有M个超储资源点，N个非超储资源点，则调剂方案中最多有M×N个调剂过程，因此，粒子群算法的解空间的维度为M×N。为描述方便，每个粒子的位置用M×N矩阵表示。

在仿真运行结束后，重新对每个资源点进行超储/欠储分析，对于仍然处于超储/欠储状态的资源点，其超储/欠储数量可对粒子的下一次运动提供“引导”，即

①实施调剂的超储资源点m′，在调剂之后仍处于超储状态。因此，在下一次迭代时，需继续从该资源点向其他资源点调剂器材，对粒子的引导作用为：

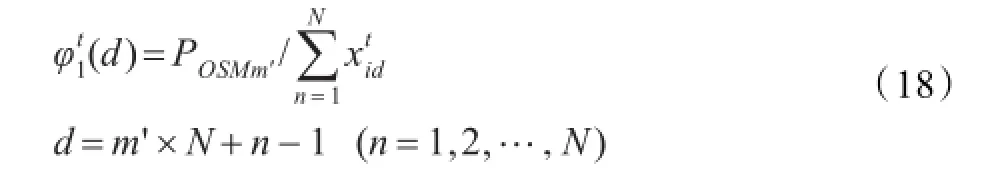
式中POSMm′为资源点m′的超储数量。所有与m′相关的维度d，都被该资源点的超储信息所引导，在粒子的下一次运动中将在这些维度上提高速度（增加调剂量）。

②实施调剂的超储资源点m′，在调剂之后处于欠储状态。因此，在下一次迭代时，需要适当减少从该资源点的调剂数量，对粒子的引导作用为：

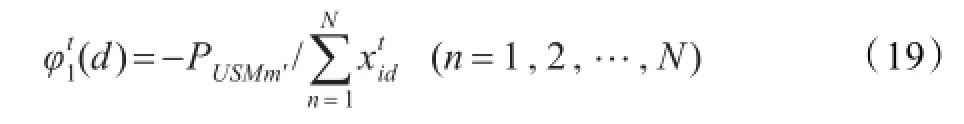
式中PUSMm′为资源点m′的欠储数量。

③接受调剂的资源点n′，在调剂之后处于超储状态。在下一次迭代中，适当减少向该资源点的调剂，对粒子的引导作用为：

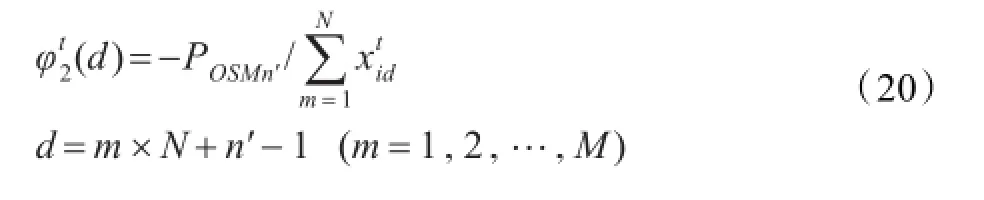
式中POSMn'为资源点n'的超储数量。

④接受调剂的资源点n′，在调剂之后仍处于欠储状态。在下一次迭代中，适当增加项向该资源点的调剂，对粒子的引导作用为：

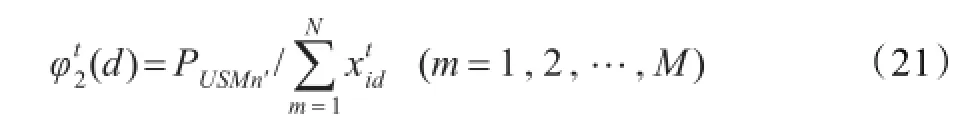
式中PUSMn′为资源点n′的欠储数量。

（2）μt的确定

一般情况下，保障体系的总体超储数量和欠储数量不会完全平衡，如果超储和欠储总数相差较大，上述引导过程可能会陷入死循环。因此，引入引导权重参数μt，随着迭代次数增加，引导的作用越来越弱。μt的计算方法为：

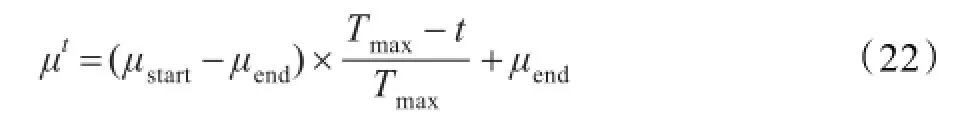
式中，μstart、μend分别为初始引导权重和算法停止时的引导权重；Tmax为算法的最大迭代次数；t为当前的迭代次数。

5　实例分析

5.1仿真实例

选取保障体系中超储/欠储情况较严重的C类器材X（器材X的单位采购成本为51元/件；单位运输成本为0.005元/件·公里；单位存储成本为2.5元/件·年）作为研究对象，该器材共涉及35个资源点使用，其中超储资源点15个，欠储资源点8个，结合器材保障业务数据库的历史消耗数据，根据文献［2］中的方法对其超储/欠储进行分析，可得各个资源点的库存信息及超储/欠储情况如表1所示。

针对当前保障体系，基于Microsoft Visual C#2010、.net平台、SqlServer数据库设计仿真系统，实验环境为IntelCorei7/2.80GHZ/4.00GB/Windows7，生成初代种群（初始的调剂方案），运行仿真，采用改进的PSO算法进行优化，求得最优的调剂方案，观察仿真优化过程并分析保障效果。

改进的PSO算法参数设置如下：系统中共有15个超储资源点（M=15），均可能向其他资源点（N=35-15=20）进行供应，则粒子的维数D为15×（35-15）=300，最大迭代次数Tmax为200次，初始粒子群的规模Ng为400，加速系数c1和c2为2，惯性权重ω=0.8，引导权重μstart=0.9，μend=0.3，引导基数φt（d）可由式（17）～（21）算得。

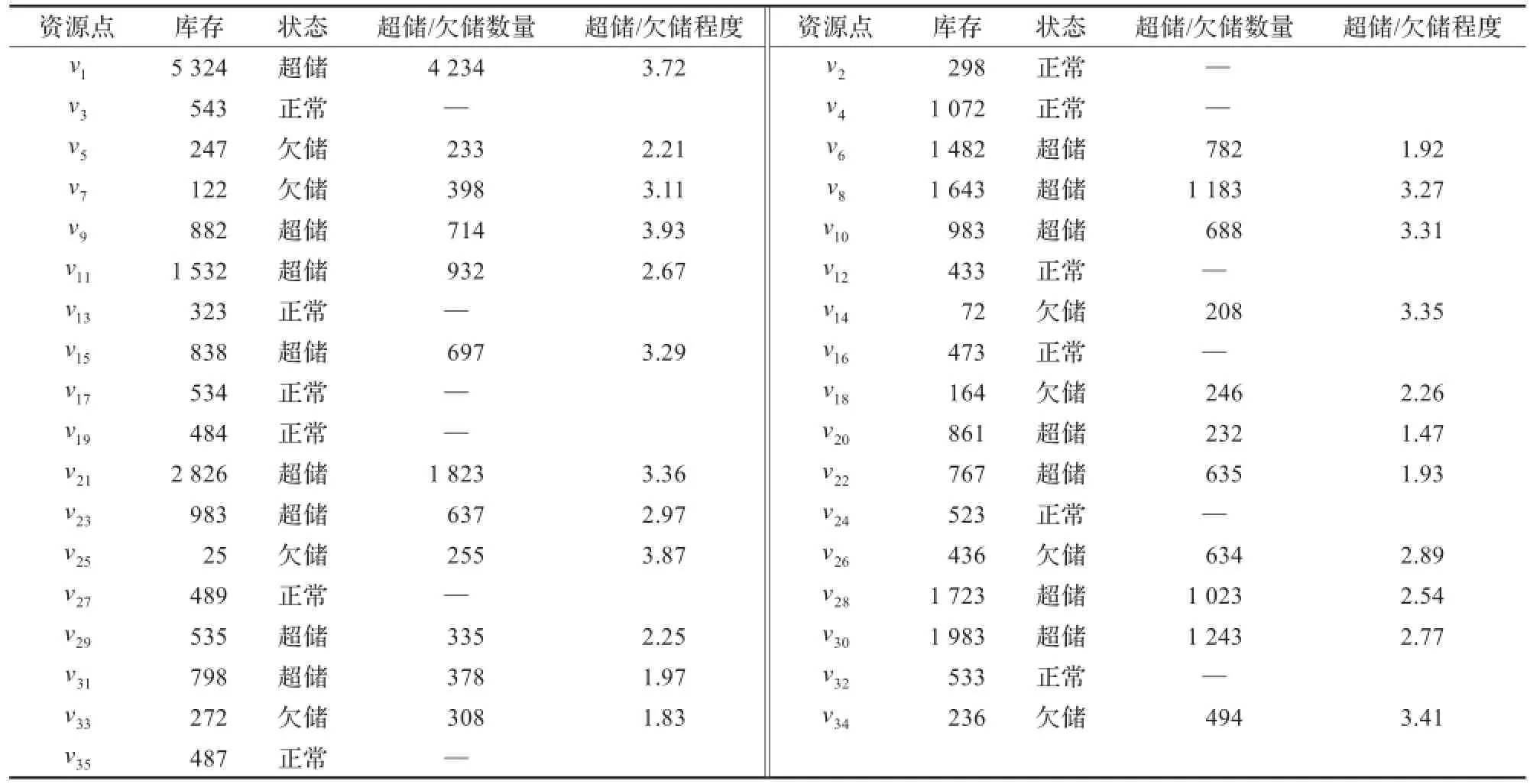
表1　资源点基本情况

5.2仿真优化结果分析

采用改进PSO算法，经200次仿真迭代后，仿真优化过程结束，历时65分钟。图2为仿真迭代优化过程中的成本曲线图。

由图2可知，在第1次迭代中，虽然调剂成本较低，但是采购成本及运输成本较高，使得保障总成本很高，说明初始种群的调剂方案不合理（调剂量偏低），调剂后仍存在较多的欠储资源点，导致后续的保障过程中频繁地进行申请、供应甚至部队自筹，消耗了较高的采购和运输成本，导致总体成本偏高；第2～50次迭代中，逐渐优化调整调剂的供应方案，增加了调剂量，虽然调剂成本随之增加，但是调剂后的采购、运输及存储成本都大幅减少，因此总的保障成本逐渐降低；第51～80次迭代中，采购、运输和存储这三部分的成本变化趋于稳定，说明调剂的调剂量基本确定，而调剂成本开始回落，说明此段仿真迭代过程开始对调剂的调度方案进行优化；第120次迭代时，优化方案趋于稳定；第150～200次迭代中，采购成本趋近于0，运输成本也降到最低，说明通过调剂，使得保障系统内的资源存储得到了有效的平衡，各级资源点不需要通过额外的器材采购满足需求。

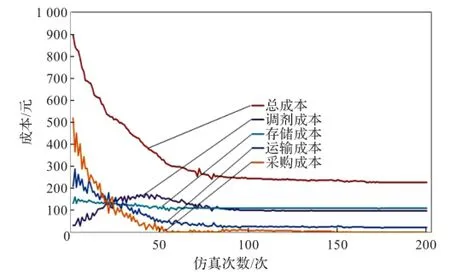
图2调剂成本与各项成本变化曲线

图3为仿真优化过程中的保障时间和保障率曲线图。随着仿真的优化，调剂的供应方案不断调整优化，保障率由原来的30%提高到98%以上，保障时间也由最初的1 000分钟以上缩短到30 min以内，保障效率得到了大幅提高。

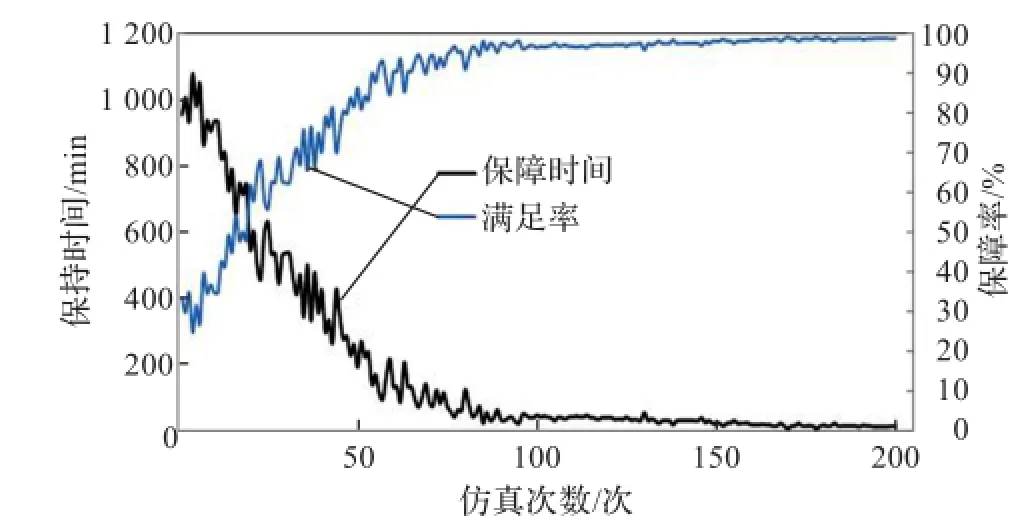
图3　保障时间与保障率变化曲线

表2为最优调剂供应方案。结合表1分析表2，实施供应的资源点为v8，v10，v11，v21，v28，v30，均为超储资源点，且相比其他超储资源点的超储程度较高，平均超储程度在3左右；需求点为v2，v5，v7，v13，v14，v18，v24，v25，v26，v33，v34，表1中所有欠储资源点都得到了一定数量的器材调剂，其中v2，v13，v24原为正常状态资源点，由于保障体系的整体资源数量偏高，也获得了一定数量的器材调剂；所有供应点实施调剂的器材数量都不超过本资源点的超储数量。

采用基本PSO算法对问题进行分析，基本参数的取值与改进PSO算法中的基本参数值完全相同，其运行结果与改进PSO算法的运行结果对比如下图4所示。

由图4可知：PSO算法在第193次仿真时才收敛到最优值，其最小总成本为275；而本文提出的改进PSO在第166次仿真时就寻找到了最优值，最小总成本为228，比PSO算法更快寻找到最优解，且最优解的值也要优于PSO算法的求解结果。

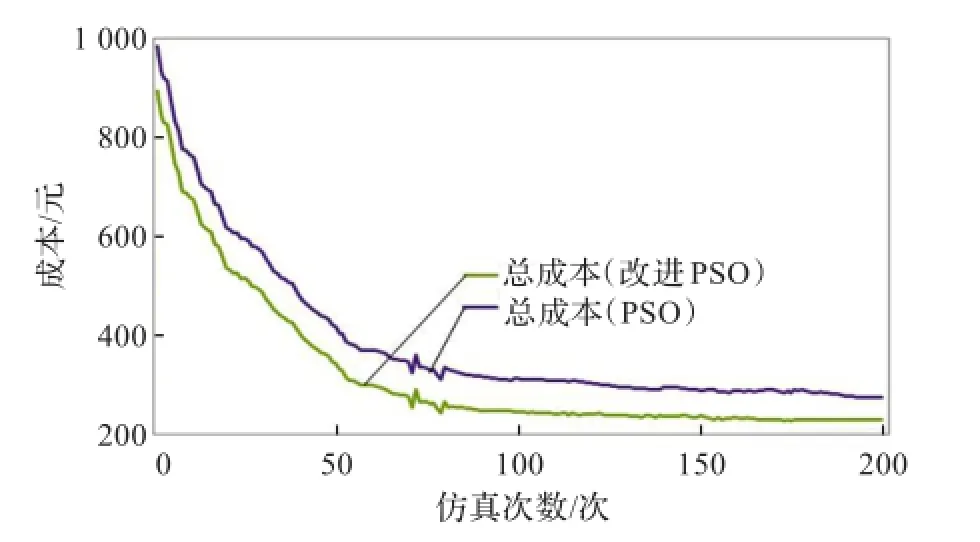
图4　改进PSO算法与PSO算法运行结果对比

6　结束语

本文对装备维修器材调剂供应的决策方法进行了研究，该方法以保障体系的资源点超储/欠储量化分析情况为数据支撑，以平衡保障体系资源存储状态、提高整体保障效率为目的，建立了调剂供应的多目标优化决策模型。针对模型的目标特点，引入引导因子设计了模型求解的改进粒子群优化算法。基于引导因子的改进PSO算法对粒子的寻优具有一定的指导作用，其收敛速度优于普通的粒子群优化算法，可应用于相关实际问题的求解。调剂供应决策是由被动的“提出申请——实施供应”转换为主动的、前瞻的供应保障。通过实施调剂，在当前装备维修器材保障体系下，可有效利用资源点超储/欠储情况进行器材资源的平衡，可有效降低保障成本、减少库存积压，从而进一步提高器材保障效率。

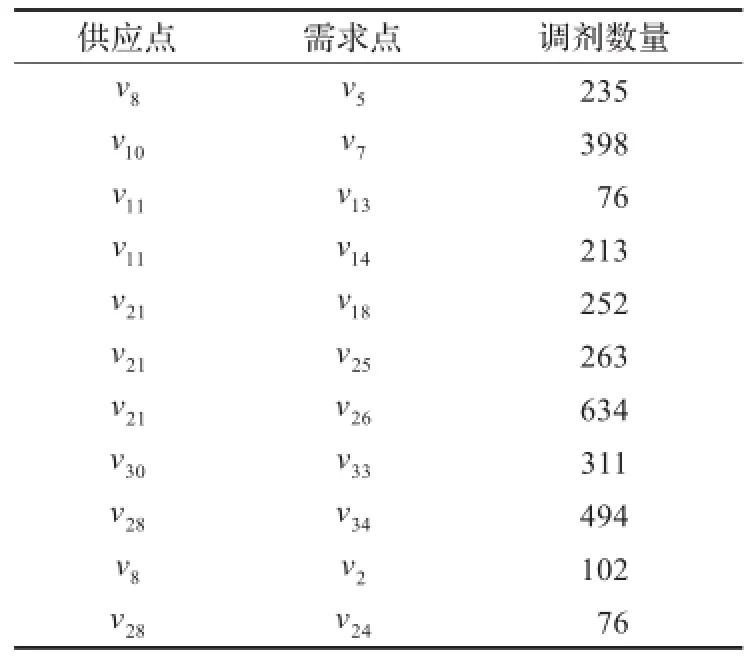
表2　调剂供应方案

［1］王铁宁.装备物流［M］.北京：国防工业出版社，2007：72-73.

［2］王铁宁，可荣博，于双双.装甲装备器材库存超（欠）储状态分析与程度评价［J］.装甲兵工程学院学报，2014，28（4）：13-18.

［3］王正元，曹继平，朱昱，等.考虑维修能力的战时备件资源配置方法研究［J］.兵工学报，2014，35（5）：719-724.

［4］孙宝琛，贾希胜，程中华.战时装备维修保障资源优化模型［J］.火力与指挥控制，2013，38（6）：159-162.

［5］朱文斌，许晓飞.基于混合粒子群算法的保障资源优化研究［J］.计算机工程与应用，2012，48（29）：210-213.

［6］张凯，赵国荣，姜静.粒子群算法在武器装备保障资源优化中的应用［J］.兵工自动化，2010，29（1）：20-23.

［7］Li Shi-Yong，Song Fei，Sun Wei.Fair resource allocation in multipath networks based on utility optimization［J］. Chinese Journal of Computers，2014，37（2）：423-433.

［8］Wu Jianshe，Chang Zhiyan，Yuan Lin.A memetic algorithm for resource allocation problem based on node-weighted graphs［J］.IEEE Computational Intelligence Magazine，2014，9（2）：58-69.

［9］牛天林，王洁，杜燕波，等.战时维修保障资源优化调度的μPSO算法研究［J］.计算机工程与应用，2011，47（9）：210-213.

［10］王涛，张伏龙，李广峰.基于多目标遗传算法的维修保障资源调度优化研究［J］.计算机测量与控制，2013，21（11）：3017-3020.

［11］高建军，蒋里强，郭强，等.基于战斗力的维修调度模型优化研究［J］.火力与指挥控制，2014，39（3）：95-98.

［12］魏国强，罗晓棠.应急资源布局与调度的模糊决策模型［J］.计算机工程，2011（22）：284-289.

［13］罗祎，阮旻智，袁志勇.多级维修供应下可修复备件库存建模与优化［J］.系统工程理论与实践，2013，33（10）：177-184.

［14］赵建忠，李海军，叶文.改进系统备件满足率约束下的备件优化配置建模［J］.兵工学报，2013，34（9）：133-138.

［15］王明亮，余勃彪.装甲装备器材仓库备件库存优化方法［J］.兵工自动化，2013，32（8）：25-28.

［16］黄照协，高崎，郝冰.三级备件保障系统下的备件库存优化模型［J］.数学的实践与认识，2014，44（1）：193-199.

［17］Gao Jindong，Zhang Yong，Zhou Fangjun.Research on control model for spare parts inventory based on the optimal replenishment cycle［C］//2013 International Forum on Computer and Information Technology，Trans Tech Publications，2014：1388-1392.

［18］Daniel M W，Ganesh K，Mohammed Y H.Position controlofelectro-hydraulicactuatorsystemusingfuzzy logic controller optimized by particle swarm optimization［J］.International Journal of Automation and Computing，2013，10（3）：181-193.

［19］杨龑亮.改进粒子群算法的无功优化［J］.黑龙江电力，2011，33（1）：33-36.

［20］Tan Guanzheng，Bao Ku.Richard Maina Rimiru.A composite particle swarm algorithm for global optimization ofmultimodalfunctions［J］.JournalofCentralSouth University，2014，21（5）：1871-1880.

［21］沈艳，郭兵，古天祥.粒子群优化算法及其与遗传算法的比较［J］.电子科技大学学报，2005，34（5）：696-699.

Decision-making of equipment maintenance materiel adjusting supply based on improved PSO.

YU Shuangshuang1，WANG Tiening1，KE Rongbo2，LI Ning3

1.Department of Technical Support，Academy of Armored Force Engineering，Beijing 100072，China
2.Unit 61377 of PLA，China
3.Unit 78416 of PLA，China

The existing problems in equipment maintenance materiel storage support is analyzed at first，then adjusting supply is put forward to alleviate the problem of imbalanced resource storage，in which the over-stocked materiel is well used to satisfy the units lack of materiel.The multi objective decision-making model of equipment maintenance materiel adjusting supply is established，and simplified adoptingε-constraint method；the improved Particle Swarm Optimization algorithm（PSO）is designed based on guiding factor to solve the model，and verified through simulation experiment.The result shows that through adjusting supply the storage resources in the support system can be balanced effectively and the support efficiency of equipment maintenance materiel is enhanced as well.

equipment maintenance materiel；adjusting supply；decision-making；improved Particle Swarm Optimization（PSO）

A

TP301.6

10.3778/j.issn.1002-8331.1502-0007

于双双（1987—），女，博士研究生，研究领域为装备信息管理与决策；王铁宁（1962—），男，博士，教授，研究领域为装备保障信息化、装备信息管理与决策、装备物流；可荣博（1985—），男，博士，研究领域为装备信息管理；李宁（1987—），男，硕士，研究领域为军事运筹学。E-mail：qingyueyingm@126.com

2015-01-30

2015-05-15

1002-8331（2015）22-0258-08

CNKI网络优先出版：2015-05-27，http://www.cnki.net/kcms/detail/11.2127.TP.20150527.1053.004.html