广义犹豫正态模糊信息集成及其多属性群决策

马庆功

常州大学怀德学院，江苏常州213016

广义犹豫正态模糊信息集成及其多属性群决策

马庆功

常州大学怀德学院，江苏常州213016

定义了犹豫正态模糊元及其运算法则、得分函数、Euclidean距离等概念；提出了广义犹豫正态模糊有序加权平均算子，并研究其性质，该算子不仅尽可能多地保留决策者的偏好信息，还可依据决策者的主观意愿选择不同的参数和属性权重，使得决策结果达到决策者的期望值；紧接着对属性权重和算子参数赋予不同的数值，获取广义犹豫正态模糊有序加权平均算子的若干种特殊算子，并探讨两个常用算子的大小关系；针对属性权重完全未知的多属性群决策问题，构建一种基于广义犹豫正态模糊有序加权平均算子的群决策方法。该方法利用同一属性下所有方案属性值间的距离求得最优权重，然后将同一方案下各属性值集结成为综合属性值，进而得到方案优劣排序。通过实例分析说明该方法的可行性和有效性。

犹豫正态模糊元；多属性群决策；信息集成算子；计算机网络系统

在管理决策分析中，由于社会的迅速发展，人们认知问题的思维和事物本身的复杂性、模糊性和不确定性，使得决策者在进行评判时，常常无法给出精确的数值。

自1965年Zadeh首先提出模糊集［1］概念之后，模糊集理论成为处理模糊信息的有效工具，并广泛地应用于风险投资、经济管理、模式识别、医疗诊断、控制理论等领域。之后，人们提出了模糊集的几种广义形式，包括：区间模糊集［2］、直觉模糊集［3］、区间直觉模糊集［4］、犹豫模糊集［5］、区间犹豫模糊集［6-7］、对偶犹豫模糊集［8］等等。Xu和Chen［9］提出了区间直觉模糊算数平均算子，并且将其应用于区间直觉模糊环境下的多属性决策过程中。徐泽水［10］研究了在直觉模糊信息环境下的各种集结算子，包括有序加权平均算子、有序加权几何算子、诱导有序加权平均算子及诱导有序加权几何算子等。Wei［11］在区间犹豫模糊环境下，提出了各种信息集成算子，并讨论了这些算子的性质。基于犹豫模糊集和直觉模糊集间的关系，Xia和Xu［12］提出了犹豫模糊信息集成算子。王坚强和李康健［13］构建了一种基于直觉正态模糊信息集结算子的决策方法，并将其应用于发动机零部件制造公司选择供应商的案例中。

随着社会的飞速发展，人们的生活中有大量的自然现象和社会现象是服从正态分布的［14］，并且运用正态模糊数表述决策信息可以更加客观准确地描述和反映现实中的数据信息。一方面，现有的模糊数的概念的论域大多是离散的，题型模糊数定义在某个确定的区间；另一方面，犹豫模糊信息将所有决策者的决策信息全面进行保留，能够防止因决策信息丢失而导致决策结果不准确的后果［15］。因此，研究定义在整个连续区间上的犹豫模糊信息及其信息集成方式具有十分重要的理论价值和现实意义。本文首先定义了犹豫正态模糊元的相关概念，然后提出了广义犹豫正态模糊信息集成算子，最后在犹豫正态环境下，基于提出的信息集成算子构建了一种新的多属性群决策方法，并以政府部门对计算机网络系统的选择为例，说明所提方法的有效性。

1　基本概念

本章首先回顾了正态模糊数的概念，然后给出犹豫正态模糊元的定义，最后提出犹豫正态元的运算法则、得分函数以及大小比较方法。

定义1.1［14］在实数域R上，称隶属函数为μA（x）=的模糊数A为正态模糊数，记为A=（a，σ）。令Ω为全体正态模糊数的集合。设Ai=（ai，σi）（i=1，2）∈Ω，则它们之间的距离公式［14］为：

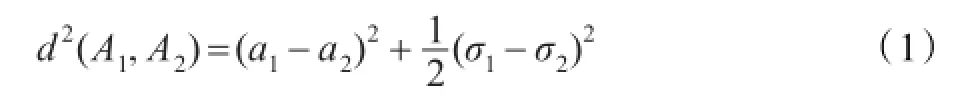
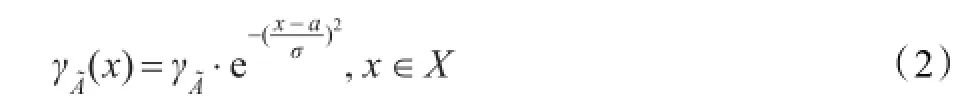
为了方便计算，记H˜为全体HNFE组成的集合。

与犹豫模糊元相比，HNFE增加了一个新的正态模糊数（a，σ），这使得其论域由离散扩展到整个连续区间，这样隶属度不再只是相对于一个模糊的概念，而是相对于该正态模糊数，能更加准确地反映决策信息，同时HNFE能全面地表达决策者们的不同决策信息，应用范围更加广泛。

接下来，将提出HNFE的运算法则，并研究它们间的运算性质。

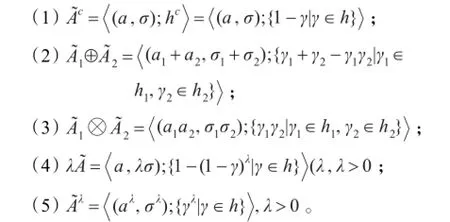
容易证明，上述定义的犹豫正态模糊运算法则满足以下性质：

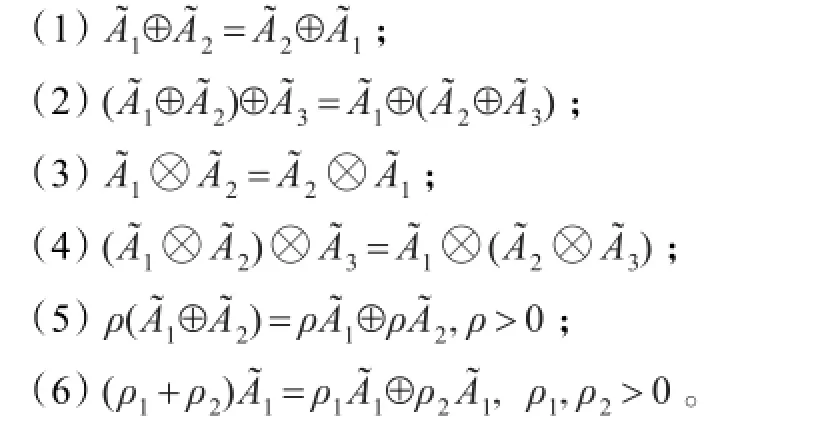
下面，将讨论HNFE的排序方法。先给出如下概念：

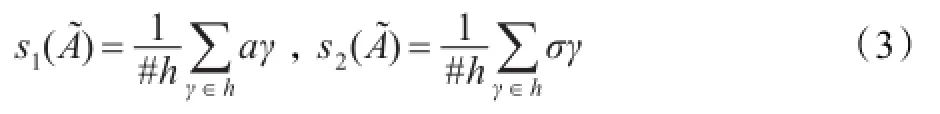
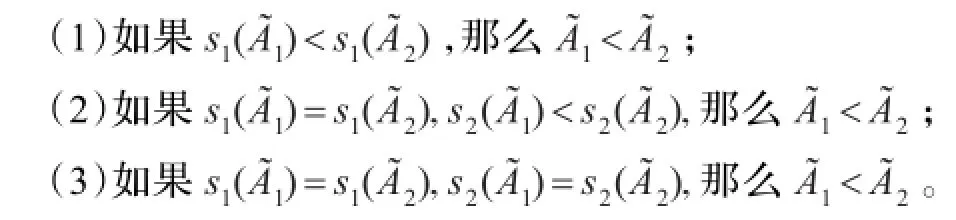
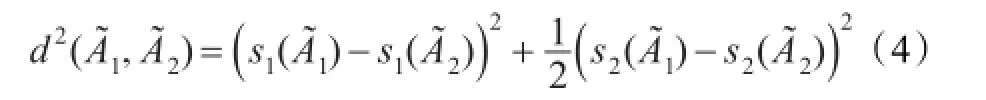
当HNFE退化为正态模糊数时，即h1=h2=｛1｝，则有，此时HNFE的距离公式也退化为正态模糊数的距离公式。

2　广义犹豫正态模糊有序加权平均算子

基于上一章定义的犹豫正态模糊运算法则，本章将提出一种广义犹豫正态模糊信息集成算子，并研究其优良性质，包括：单调性、有界性、幂等性、置换不变性。

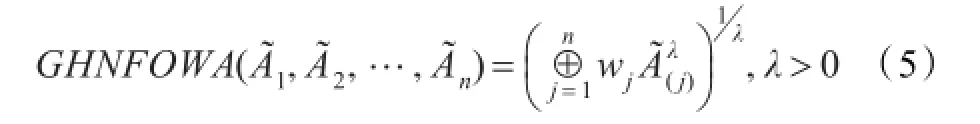
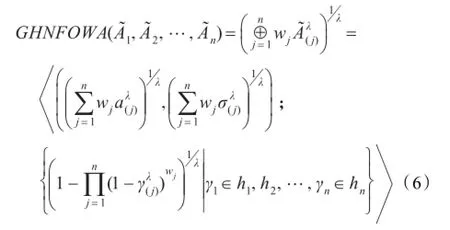
证明（1）先证明等式（6）成立。首先运用数学归纳法证明对于所有的正整数n，如下等式成立：

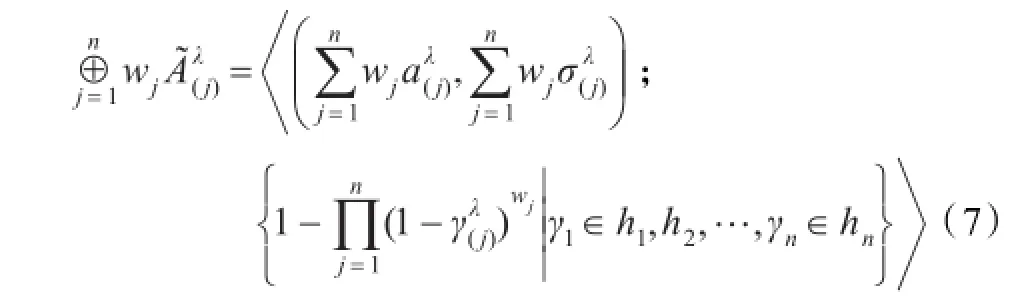
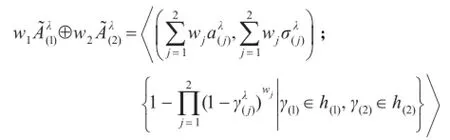
假设当n=k时，等式（7）成立，即

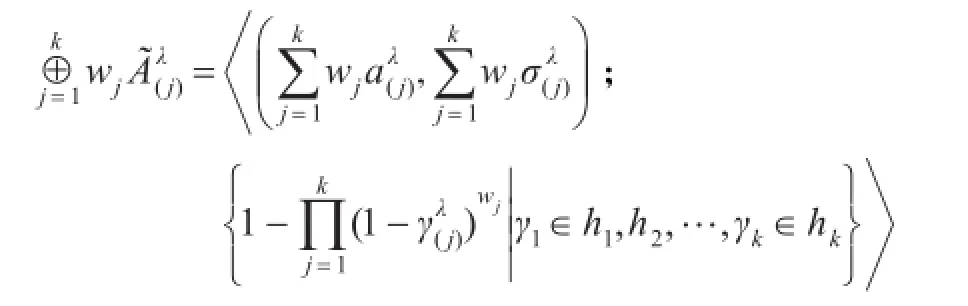
当n=k+1时，依据定义1.3，有

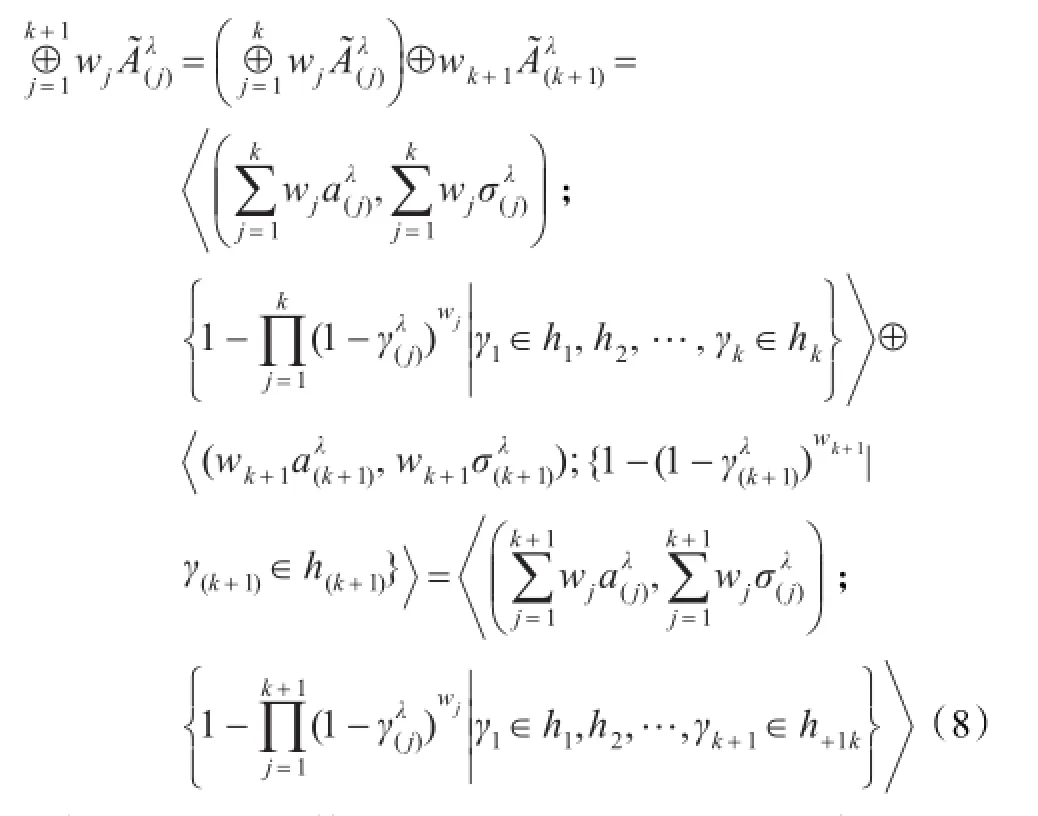
即当n=k+1时，等式（7）成立。因此，对于所有的正整数n，等式（7）成立。

由定义1.3的运算，则有

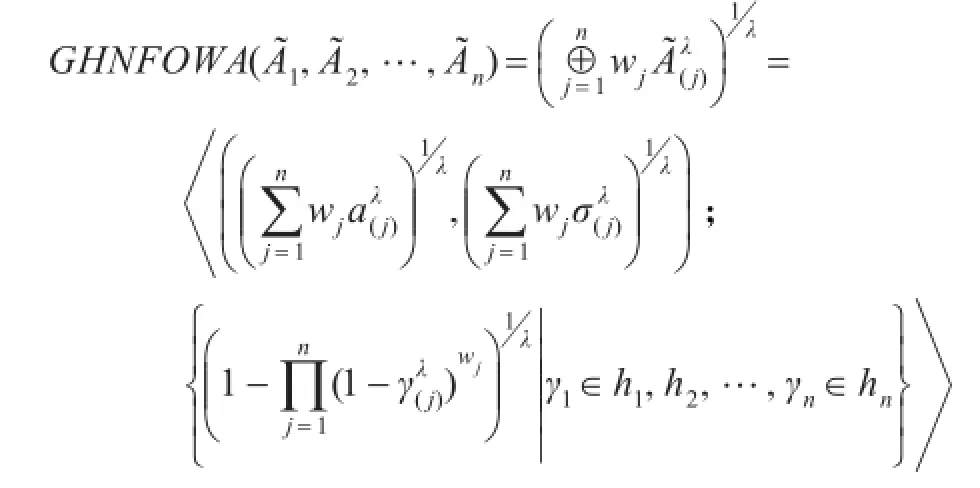
（2）接下来，需证明GHNFOWA算子的集成结果仍是一个HNFE，关键是证明对∀γ1∈h1，γ2∈h2，…，γn∈hn，有

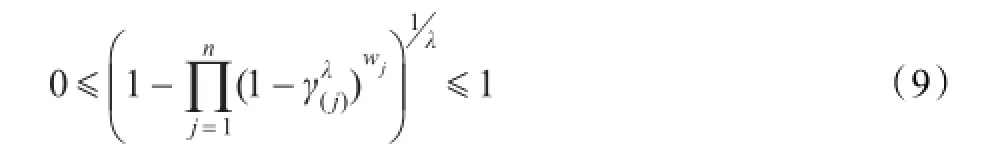
事实上，因为γ1，γ2，…，γn∈［0，1］，那么对于∀j=

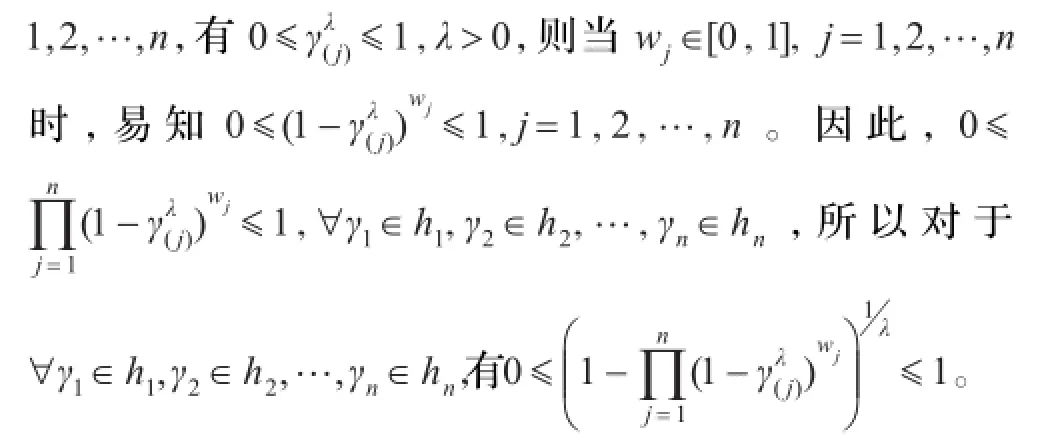
综上，定理2.1成立。

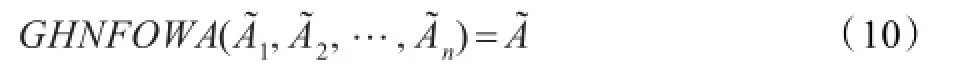
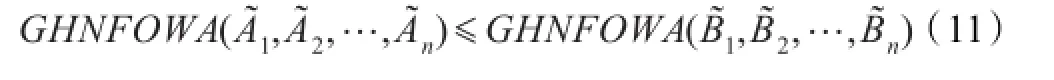
（4）置换不变性：设A˜φ（1），A˜φ（2），…，A˜φ（n）是A˜1，A˜2，…，A˜n的任意一个置换，则有

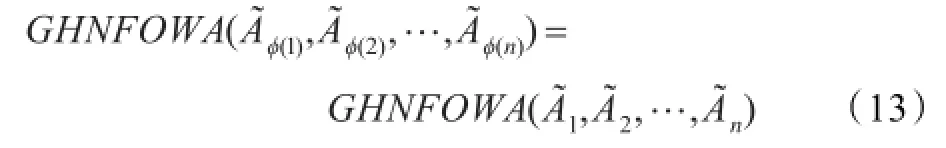
3　GHNFOWA算子的几种常见形式

首先依据权重向量w=（w1，w2，…，wn）T和参数λ取不同的数值，得到GHNFOWA算子的若干种特殊形式，然后探究其中两种常见算子的大小关系。

Case 1：权重向量w=（w1，w2，…，wn）T取不同的数值。

①若w=（1，0，…，0）T，GHNFOWA算子将变为犹豫正态模糊极大（HNF-MAX）算子，即：

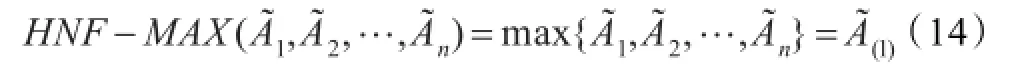
②若w=（0，0，…，1）T，GHNFOWA算子将变为犹豫正态模糊极小（HNF-MIN）算子，即：

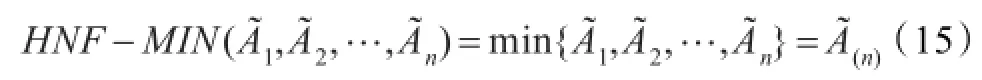
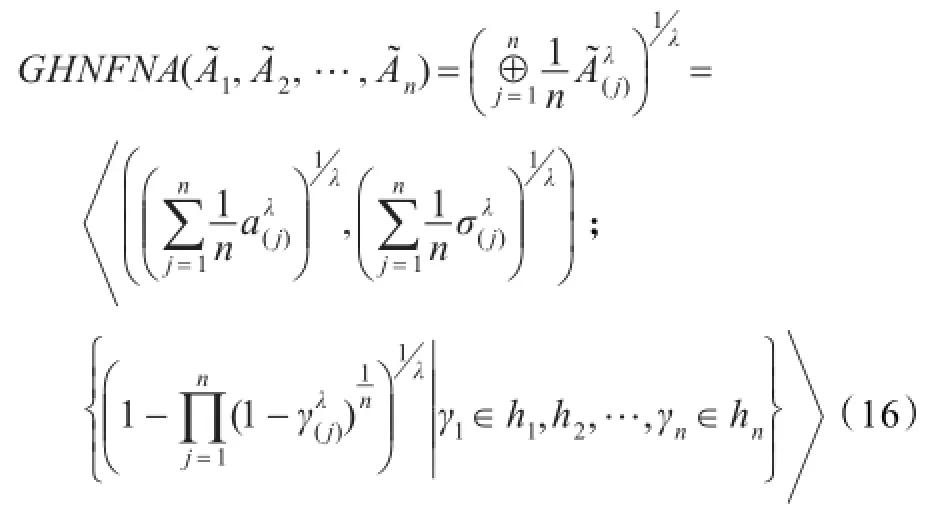
Case 2：参数λ取不同的数值。

如果λ=1时，GHNFOWA算子将会退化为犹豫正态模糊有序加权算术平均（HNFOWAA）算子：

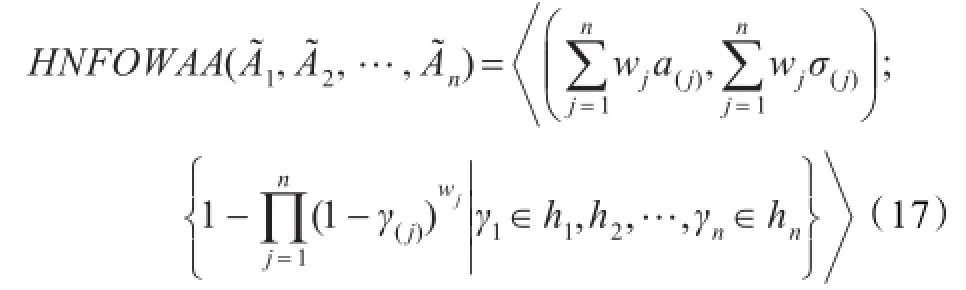
如果λ→0时，GHNFOWA算子将会退化为犹豫正态模糊有序加权几何平均（HNFOWGA）算子：

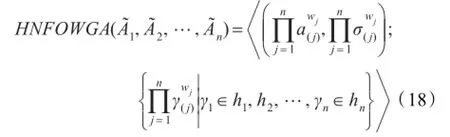
接下来将探究这两个常用的算子，即犹豫正态模糊有序加权算术平均（HNFOWAA）算子和犹豫正态模糊有序加权几何平均（HNFOWGA）算子之间的大小关系，为此，先引入以下引理：

引理3.1［15］假设xj＞0，λj≥0，j=1，2，…，n，并且，则有。当且仅当x1=x2=…=xn时，等号成立。

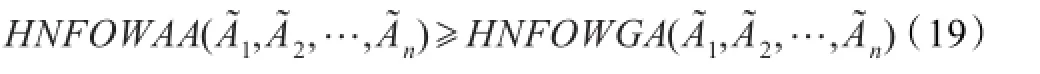
证明为了方便计算，令

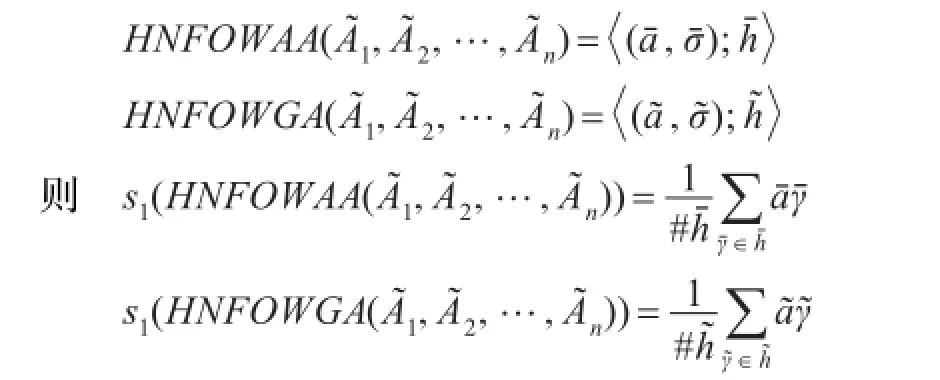
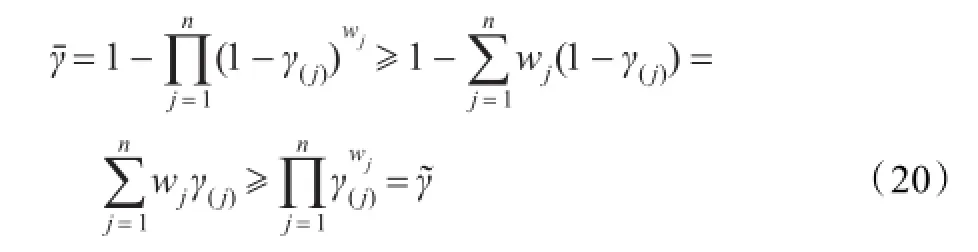
依据定义1.5，有：因此结论成立。

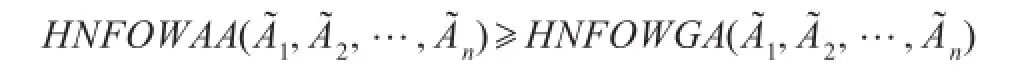
定理3.1表明运用HNFOWAA算子得到的犹豫正态模糊元不小于运用HNFOWGA算子得到的犹豫正态模糊元。

4　基于GHNFOWA算子的多属性群决策方法

基于GHNFOWA算子提出一种新的多属性群决策方法，其中的属性权重为实数，属性值以HNFE的形式表示。

考虑犹豫正态模糊多属性群决策问题，假设有m个可行方案Y1，Y2，…，Ym，伴随每个方案的属性集合为C=｛C1，C2，…，Cn｝，关联权重向量w=（w1，w2，…，wn）T完全未知，其满足。在决策过程中，每个决策者都给出可行方案Yi在属性Cj下的偏好信息。由于每个决策者提供的偏好信息不一定相同，因此这些偏好信息就构成了可行方案Yi在属性Cj下的HNFE，则所有决策者提供的可行方案集在属性集下的决策偏好信息可构成一个犹豫正态模糊信息决策矩阵。

针对上述问题，给出基于广义犹豫正态模糊信息集成的多属性群决策方法，具体步骤如下：

步骤1标准化处理

①当Cj为效益型属性时，，其中；

②当Cj为成本型属性时，，其中。

步骤2确定属性权重

在进行多属性决策时，如果某一属性下的所有方案属性信息差异越小，则说明该属性能够给决策者提供的决策信息量就越少，于是在决策过程中的重要性就越低，则应该赋予这个属性的权重就越小。反之，若所有方案在某一属性下的属性值有明显的差异，则表明该属性能够给决策者提供较多的决策信息，那么该属性在决策过程中就越重要，则应赋予其较大的权重。因此若属性Cj（j=1，2，…，n）的权重信息完全未知，则可通过以下方法确定权重wj：

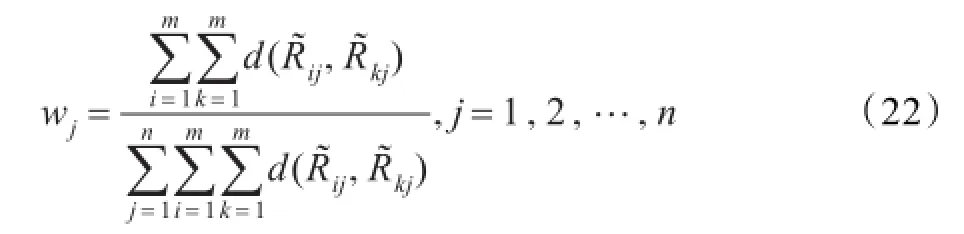
步骤3集结可行方案的综合属性值

依据标准决策矩阵R˜和提出的GHNFOWA算子，计算每个可行方案Yi（i=1，2，…，m）的综合属性值R˜i（i=1，2，…，m），即

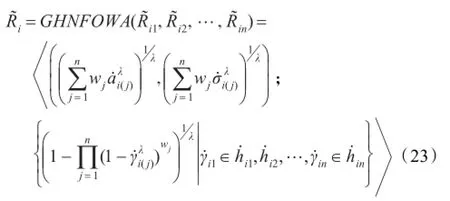
步骤4计算均值得分函数和标准差得分函数

步骤5可行方案优劣排序

运用定义1.5中的排序方法，对可行方案Yi（i=1，2，…，m）进行优劣排序，并选择出最优的决策方案。

表1　决策者提供的犹豫正态模糊决策矩阵˜=）4×4

表1　决策者提供的犹豫正态模糊决策矩阵˜=）4×4

C1 C2 C3 C4 Y1 Y2Y3 Y4＜（7.1，2.1），｛0.45，0.65｝＞＜（4.1，3.0），｛0.32，0.50｝＞＜（8.6，1.9），｛0.55，0.69｝＞＜（9.2，1.2），｛0.54，0.65｝＞＜（4.1，1.8），｛0.35，0.57｝＞＜（6.8，1.0），｛0.15，0.28｝＞＜（6.2，2.1），｛0.60，0.85｝＞＜（7.1，2.4），｛0.40，0.72｝＞＜（5.7，1.7），｛0.45，0.63｝＞＜（7.1，3.0），｛0.39，0.64｝＞＜（5.4，2.4），｛0.62，0.73｝＞＜（6.1，2.0），｛0.40，0.52｝＞＜（4.8，0.6），｛0.59，0.77｝＞＜（5.1，1.7），｛0.70，0.81｝＞＜（6.2，2.5），｛0.65，0.72｝＞＜（7.1，1.3），｛0.49，0.64｝＞

5　案例分析

考虑一个计算机网络系统选择问题。某政府机关欲通过计算机网络和通信等现代信息技术手段，实现政府组织结构和工作流程的优化重组，超越时间、空间和部门分隔的限制，建成一个精简、高效、廉洁、公平的政府运作模式，以便全方位地向社会提供优质、规范、透明、符合国际水准的管理与服务。该政府采购部门现将从现有4套计算机网络系统Yi（i=1，2，3，4）中选择一套计算机网络系统进行安装。为了选择一套性能最优的计算机网络系统，该政府采购部门将对四套系统分别在以下四个性能指标下进行综合评估，即C1网络速率；C2系统利用率；C3带宽；C4硬件设施，最终选择性能一套最优的计算机网络系统。为了保证决策评估的客观性和权威性，该政府采购部门邀请了不同领域的专家，依据自身的专业知识和实际经验，并结合四套计算机网络系统在测试过程中的表现出对这四套系统在上述4个属性指标下进行性能满意度测评，给出了表1所示的犹豫正态模糊决策矩阵。下面依据本文提出的犹豫正态模糊多属性群决策方法，遴选出综合性能最强的计算机网络系统。

步骤1标准化处理

由于C1，C2，C3和C4都是效益型属性，则通过标准化方法（a）对犹豫正态模糊决策矩阵D˜进行处理，得到标准化决策矩阵，如表2所示。

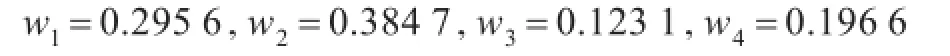
步骤3运用GHNFOWA算子分别计算出每套计算机网络系统Yi（i=1，2，3，4）的综合属性值以备选系统Y2为例，令λ=1，计算综合属性值为：

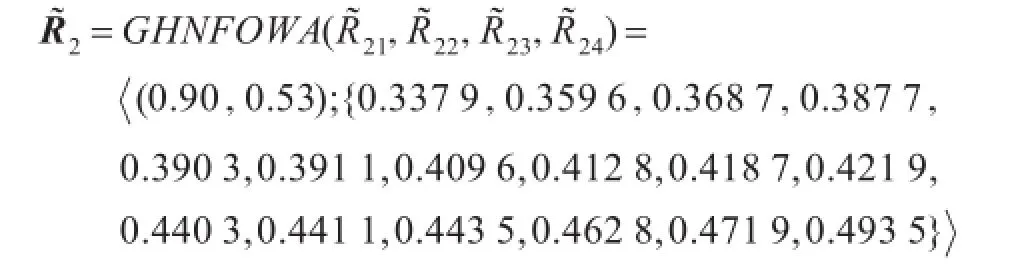
步骤4计算在不同参数下每套计算机网络系统的综合属性值R˜i（i=1，2，3，4）的均值得分函数1，2，3，4），结果见表3。

步骤5依据定义1.5，在不同的参数下对四套计算机网络系统Yi（i=1，2，3，4）进行优劣排序，排序结果见表3。从表3可知，当参数λ取不同的数值时，排序结果基本一致，且综合性能最优的计算机网络系统均为Y3。

为了说明本文提出群决策方法优良性能，将本文的决策方法与文献［12］中的决策方法进行对比分析。依据文献［12］中的犹豫模糊决策方法处理上述问题。

首先，构建犹豫模糊决策矩阵D=（hij）4×4，其中hij为表1中每个HNFE除去均值和标准差后的犹豫模糊元。

然后利用文献［12］中的公式（27），将每套计算机网络系统在各个属性指标下的属性值集结成为综合属性值hi（i=1，2，3，4）（同样地，计算当λ→0，λ=1，λ=2，λ=5，λ=10时的综合属性值），由于hi由16个数值组成，因篇幅的限制，故在此省略。

接着，依据犹豫模糊元的得分函数公式，计算不同参数下每套计算机网络系统综合属性值hi（i=1，2，3，4）的得分函数值s（hi）（i=1，2，3，4），见表4。

表2　标准化的犹豫正态模糊决策矩阵˜=）4×4

表2　标准化的犹豫正态模糊决策矩阵˜=）4×4

C1 C2 C3 C4 Y1Y2 Y3 Y4＜（0.6，0.6），｛0.45，0.65｝＞＜（1.0，0.4），｛0.32，0.50｝＞＜（0.5，0.6），｛0.55，0.69｝＞＜（0.4，1.0），｛0.54，0.65｝＞＜（0.6，0.7），｛0.35，0.57｝＞＜（0.9，0.4），｛0.15，0.28｝＞＜（0.9，0.9），｛0.60，0.85｝＞＜（1.0，1.0），｛0.40，0.72｝＞＜（0.8，0.6），｛0.41，0.63｝＞＜（1.0，1.0），｛0.39，0.64｝＞＜（0.8，0.8），｛0.62，0.73｝＞＜（0.9，0.7），｛0.48，0.52｝＞＜（0.7，0.4），｛0.59，0.77｝＞＜（0.7，0.7），｛0.70，0.81｝＞＜（0.9，1.0），｛0.65，0.72｝＞＜（1.0，0.5），｛0.49，0.64｝＞

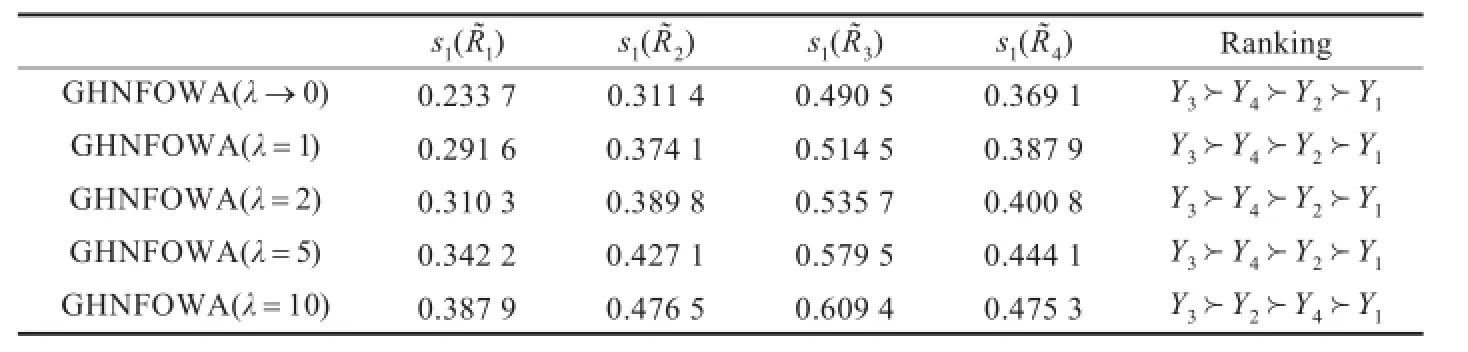
表3　利用GHNFOWA算子计算四套计算机网络系统的均值得分函数值和优劣排序

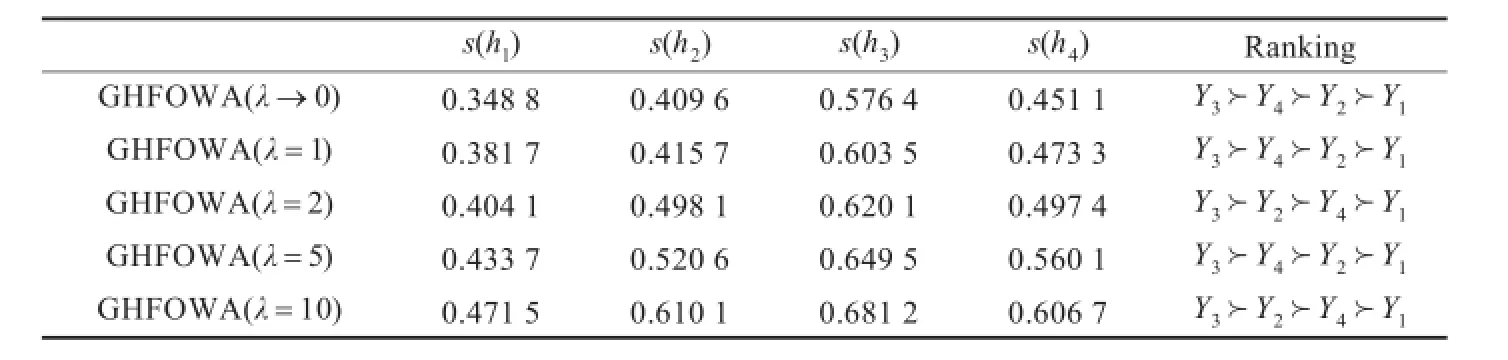
表4　利用GHFOWA算子计算四套计算机网络系统的得分函数值和优劣排序

根据得分函数值的大小对这四套计算机网络系统进行优劣排序，结果如表4所示。分析比较发现，运用本文方法得到的结果与文献［12］中方法得到的结果一致，表明本文提出的群决策方法是可行的和有效的。但是本文提出的决策方法相对于文献［12］中的决策方法有以下优势：首先，正态分布广泛存在于各种自然现象、社会现象和生产实践活动中，运用犹豫正态模糊元表述决策信息可以更加客观准确地反映现实中的数据信息；其次，犹豫正态隶属函数具有高阶导数连续的性质，而其他几种模糊数都不具有这种性质［16］；再次，本文提出的决策方法使用范围更为广泛，由于文献［12］中提出的几何算子其实是本文提出的GHNFOWA算子的一种特殊形式，因此本文的决策方法实用性更强，拓展了犹豫模糊理论的应用范围；最后，本文提出用HNFE刻画模糊概念更能贴近人类思维，尽可能多地保留了决策者的偏好信息，并且利用本文提出的决策方法进行决策时，决策者可以依据自身的偏好和乐观态度选择不同的参数进行信息集成，从而使得决策过程更具有一定的灵活性，而且能有效的体现决策者的决策意愿。

6　结论

本文首先将离散空间上的犹豫模糊元推广到连续空间，给出了HNFE及其相关概念，并且定义了犹豫正态模糊运算法则；其次，基于这些运算法则，提出了广义犹豫正态模糊有序加权平均算子，并研究了其相关优良性质；接着给出了GHNFOWA算子的一些常用形式；针对属性权重完全未知的犹豫正态模糊多属性群决策问题，构建了一种基于GHNFOWA算子的决策方法。该决策方法利用HNFE间的距离确定属性权重，再基于提出的GHNFOWA算子计算得到各方案的综合属性值，进而确定方案的优劣排序。最后将提出的决策方法应用于政府部门对计算机网络系统的选择过程中，并将本文方法与现有的决策方法进行比较分析，以验证提出的决策方法是可行的和有效的。因此，本文的研究成果具有一定的理论价值和现实意义。

［1］Zadeh L A.Fuzzy sets［J］.Information and Control，1965，8（3）：338-356.

［2］Turksen I B.Interval valued fuzzy sets based on normal forms［J］.Fuzzy Sets and Systems，1986，20：191-210.

［3］Atanassov K T.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20（1）：87-96.

［4］Atanassov K，Gargov G.Interval-valued intuition-istic fuzzy sets［J］.Fuzzy Sets and Systems，1989，31：343-349.

［5］Torra V.Hesitant fuzzy sets［J］.International Journal of Intelligent Systems，2010，25：529-539.

［6］Chen N，Xu Z S，Xia M M.Interval-valued hesitant preference relations and their applications to group decision making［J］.Knowledge-Based Systems，2013，37：528-540.

［7］Chen N，Xu Z S，Xia M M.Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis［J］.Applied Mathematical Modelling，2013，37：2197-2211.

［8］Zhu B，Xu Z S，Xia M M.Dual hesitant fuzzy sets［J］. Journal of Applied Mathematics，2012，32（5）：317-386.

［9］Xu Z S，Chen J.Approach to group decision making based on interval-valued intuitionistic judgment matrices［J］.Systems Engineering-Theory and Practice，2007，27：126-133.

［10］Xu Z S，Intuitionistic fuzzy aggregation operators［J］.IEEE Transactions on Fuzzy Systems，2007，15：1179-1187.

［11］Wei G W，Zhao X F，Lin R.Some hesitant interval-valued fuzzy aggregation operators and their applications to multiple attribute decision making［J］.Knowledge-Based Systems，2013，46：43-53.

［12］Xia M M，Xu Z S.Hesitant fuzzy information aggregation in decision making［J］.International Journal of Approximate Reasoning，2011，52：395-407.

［13］王坚强，李康健.基于直觉正态模糊集结算子的多准则决策方法［J］.系统工程理论与实践，2013，33（6）：1501-1508.

［14］Wang J，Zhou P，Li K，et al.Multi-criteria decision-making method based on normal intuitionistic fuzzy-induced generalized aggregation operator［J］.TOP，2014：1-20.

［15］Torra V，Narukawa Y.Modeling decisions：information fusion and aggregation operators［M］.［S.l.］：Springer，2007.

［16］李德毅，刘常昱.论正态云模型的普适性［J］.中国工程科学，2004，6（8）：28-34.

Generalized hesitant normal fuzzy information aggregation and their application to multi-attribute group decision making.

MA Qinggong

Changzhou University Huaide College，Changzhou，Jiangsu 213016，China

Hesitant normal fuzzy elements（HNFEs）as well as their operational laws，score functions and Euclidean distance are defined.Then，the generalized hesitant normal fuzzy ordered weighted averaging（GHNFOWA）operator is proposed and some desirable properties of the GHNFOWA operator are studied.The GHNFOWA operator not only preserves the decision maker’s preference information as much as possible，but also the values of the parameter and attribute weights can changes on the base on decision makers’attitude to make the results fix the expected values of decision makers. Furthermore，some special cases of the GHNFOWA operator are given when the weight vector and operator parameter takes different values，and the relationship between two common operators is studied.Finally，for multi-attribute decision making problems with the information of attribute weights is completely unknown，a method based on the GHNFOWA operator is investigated.The optimal weights are calculated by the distances of each alternative under an attribute，and then aggregate all the attribute values into the overall attribute values，which is followed by the ranking of the alternative. An example is given to demonstrate the developed method is practicality and effectiveness.

hesitant normal fuzzy elements；multi-attribute group decision making；information aggregation operator；computer network systems

A

O22

10.3778/j.issn.1002-8331.1503-0068

江苏省科技支撑计划（工业）重点项目（No.BE2013005-3）；靖江市科技局产学研项目（No.CDHJK1501001）。

马庆功（1980—），男，硕士研究生，工程师，研究方向：电子技术及应用。E-mail：2985390216@qq.com

2015-03-08

2015-05-06

1002-8331（2015）22-0134-07

CNKI网络优先出版：2015-05-27，http://www.cnki.net/kcms/detail/11.2127.TP.20150527.1053.001.html