平头塔机起重臂下主弦杆设计计算方法的研究

范开英，沈兰华，史海红

（山东丰汇设备技术有限公司，山东 济南 250200）

平头塔机起重臂下主弦杆设计计算方法的研究

范开英，沈兰华，史海红

（山东丰汇设备技术有限公司，山东 济南 250200）

随着建设项目对起重量和幅度越来越高的要求，平头塔机应用越来越广泛。在对整机影响最大的起重臂设计时，精确的设计计算结果对节约成本意义重大。本文为平头塔机局部理论设计特别是起重臂下主弦杆总结了清晰的计算思路，分析了理论计算与有限元分析结果的差异性，并提出了一些优化控制方法。

平头式塔式起重机；起重臂；下主弦杆；设计

与传统带塔帽和拉杆的平臂塔机相比，平头塔机因其构造的不同有着得天独厚的优势［1］：它可以降低拆装塔机对所需起重设备的要求；因塔群交叉作业总体高度可大大降低，尤其适合于群塔交叉作业；吊臂钢结构寿命长、安全性高。平头塔机目前在电站建设等大型项目上应用越来越多，对其构造的经济性分析也十分重要。

平头塔机起重臂自重对平衡臂和塔身设计有较大影响，如果起重臂自重增加10%，则一般平衡臂增加10%，塔身增加5%，导致整机重量大幅增加。每减少1t起重臂重量，大约可减少0.5t平衡臂、1t平衡重、3～5t塔身材料。因此起重臂的精确设计在平头塔机设计中非常重要。然而在对起重臂进行设计计算时，发现起重臂下主弦杆有限元软件分析结果与手工计算结果相差较大，往往手工计算合格时，有限元分析结果却不满足要求。

1 起重臂下主弦设计计算

采用倒三角结构，小车在起重臂的下主弦杆工字钢上行走。起重臂为桁架悬臂结构，下主弦杆设计校核分为三种工况。

1）起升载荷在起重臂最大幅度，下主弦杆轴力由自重弯矩和起升载荷弯矩组合而成。

式中 MGj——计算节数j节的自重力矩；

MQj—— 计算节数j节的起升载荷力矩，Q70对应的为远端载荷，此MQj为起升载荷能产生的最大力矩；

Gi——计算节数i节的自重载荷；

Li——计算节数i节的自重重心；

Lj——计算节数j节的计算位置；

Nj——计算节数j节的下主弦杆载荷。由起升特性可知，各幅度起升载荷对塔身产生的力矩相同，即

起重臂在任意载荷作用下的各处弯矩为

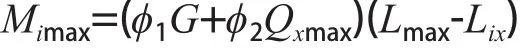
由此可知对起重臂各位置，力矩最大值为最大幅度起升载荷产生力矩。因此在取起升载荷的力矩时统一选取最大幅度的起升载荷在各处引起的弯矩即可。通过对应力的控制，可计算出下主弦杆的截面积。

2）小车在下主弦杆节间某处，下主弦杆承受自重弯矩引起的轴压力，节间跨中弯矩引起的工字钢上翼缘板的局部弯曲应力共同作用。

3）小车在下主弦杆节点处时，小车局部轮压引起的工字钢下翼缘板的局部弯曲应力最大值为

起重臂下主弦杆工字钢为左右对称结构，在设计时共有6个未知参数。腹板高度由车轮高度决定，下翼缘板宽度由车轮间距决定；当起重臂腹杆截面确定后，腹杆在上翼缘板布置时，为避免焊缝集中，通常会错开焊接，上翼缘板最小宽度确定。由工况一可计算出下主弦杆的总截面积，由工况二可校核出上翼缘板的厚度是否满足上翼缘板局部抗弯要求；由工况三可校核出下翼缘板的厚度是否满足局部轮压要求；对选择好的截面，还要校核翼缘板和腹板的构造稳定性要求；至此下主弦杆工字钢截面确定。

2 起重臂下主弦杆有限元分析

起重臂为桁架结构，建模时选用Beam188单元［2］，它适合于分析从细长到中等粗短的梁结构，该单元基于铁木辛哥梁结构理论，并考虑了剪切变形的影响。由于起重臂各节工字钢截面的型心高度不一致，在手工计算时通常忽略这一问题。另外由于上翼缘板的宽度很小，起重臂各节腹杆的交点并不在同一条直线上。为保持与设计计算统一，选取斜腹杆交点在同一条中心线上，起重臂下主弦杆根据实际情况调整高度，使下翼缘板上表面在同一水平面上。在梁单元偏心设置时，调整量为下翼缘板厚度和一半腹板高度之和。

QTZ1200塔机起重臂根部梁高3 000mm，最大幅度70m，起升性能13.1t，小车吊钩及钢丝绳重量共计5.5t，按规范计算得起升载荷为21.5t，在起重臂下主弦杆70m小车作用处加载。根据起重臂实际重量设置密度为9 360kg/m3。起重臂根部约束按Y向铰接，其余固定约束计算。计算结果如图1、图2所示。

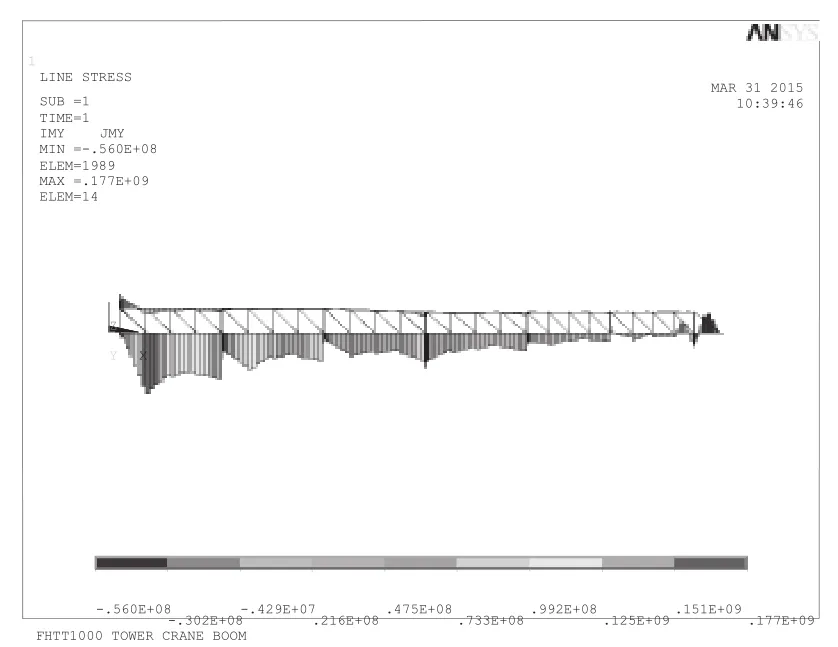
图1 起重臂Y轴方向局部弯矩图

图2 起重臂Von应力结果图

3 理论计算和有限元结果比较

从计算表中可以看出，设计校核计算的结果“下主弦杆理论轴力”与Ansys建模计算的结果“模型计算轴力”基本相同，误差在3%以内，这是因为实际局部情况与模型结构均匀的自重情况略有差异，这些误差可以忽略。

考虑第四强度理论-形状改变比能理论，Ansys模型计算出来的冯氏应力即表格中的“模型综合应力”与轴应力比较则大很多，一般在10%～15%左右，而传统的设计计算方法目前则无法计算此项。通过另一种有限元分析软件SAP84的分析，此弯矩是确实存在的，而且两种有限元软件分析的结论基本相同，所以只靠传统设计计算方法存在设计隐患。

表1 起重臂理论计算与有限元结果对比

4 局部弯矩影响的优化

根据起重臂下主弦杆设计计算可知，起重臂各节截面积差距较大，为统一车轮，上下翼缘板面积也各不相同，形心差从节1到节6依次为 2.5，-18.6，-15.5，-12.4，-22，-48，局部弯矩引起的应力误差与形心分布没有明显的关系，但形心下移似乎对减小应力有好处。

经模型反复调整比较，桁架高度减少60mm，下主弦杆结构向桁架中心线以下调60mm，此时下主弦杆的轴力虽有增大，但局部弯矩显著减少，综合应力略有下降。

5 结 论

本文总结了平头塔机起重臂下主弦杆设计计算中应注意的问题，明确了工字钢截面各参数的设计和校核原则。综合上述分析，起重臂下主弦杆的设计要考虑的因素如下。

1）工字钢截面积为求解参数，下翼缘板宽和腹板高度为公共结构参数；上翼缘板宽度、厚度为腹杆构造要求和局部弯矩校核参数；下翼缘板厚度为局部轮压校核参数。

2）传统的设计计算结果不能完全体现起重臂下主弦杆的受力情况，设计之初应预留15%的余量，以保证在局部弯矩的影响下起重臂强度仍能满足要求。

3）有限元建模时应考虑形心位置的影响，虽然实际中形心变化是不可避免的，但可以利用腹杆对桁架高度的变化减少其对局部弯矩的影响。

［1］常晓华，王春华.塔式起重机起重臂危险点的确定［J］.建筑机械化，2006，（10）：21-23.

［2］任会礼，李江波，高崇仁.基于ANSYS的塔式起重机臂架有限元参数化建模与分析［J］.起重运输机械，2005，（9）：11-13.

［3］张志文.起重机设计手册（第一版）［M］.北京：中国铁道出版社，2001.

（编辑 贾泽辉）

Research of design and calculation method of main chord member under the fl at head tower crane boom

FAN Kai-ying， SHEN Lan-hua， SHI Hai-hong

TH212；TH213.3

B

1001-1366（2015）08-0039-03

2015-05-09