平头式塔机起重臂预翘度的设计研究

李 斌，李宏乾

（沈阳建筑大学 交通与机械工程学院，辽宁 沈阳 110168）

平头式塔机起重臂预翘度的设计研究

李 斌，李宏乾

（沈阳建筑大学 交通与机械工程学院，辽宁 沈阳 110168）

针对平头式塔式起重机起重臂在工作中产生的下挠问题，研究起重臂预翘度确定的理论和方法。通过研究起重臂在自重载荷和起重载荷的共同作用下，起重臂的下挠曲线和下挠量的计算分析方法，给出了起重臂挠曲线和下挠量的计算表达式。依据最大下挠量最小的原则确定了起重臂预翘度的设计方法和计算表达式，为平头式塔式起重机的起重臂预翘度的设计奠定理论基础。

平头式塔式起重机；下挠曲线；设计方法；预翘度

平头式塔式起重机在起重作业时，塔机起重臂在自重载荷和起重载荷共同作用下会出现不同程度的下挠。过大的下挠会减少塔机的实际起升高度，并使载重小车由大幅度向小幅度变幅过程中出现爬坡现象。

为解决这一问题，塔机设计者在设计时都使起重臂各节臂架的上弦杆长度略小于下弦杆的长度，以实现起重臂具有一定的预翘量，来抵消起重臂的下挠。但是这种设计还仅仅是基于经验的基础上，并没有理论依据。为解决这一问题，本文运用结构在载荷作用下的弹性变形理论，研究起重臂在自重载荷和起重载荷共同作用下所产生的变形曲线和各节臂架端部的转角和位移计算方法。并以相对水平轴线最大下挠量最小为原则确定了起重臂预翘度设置的理论和方法。以实现起重臂在合理的预翘度下使起重小车的最大爬坡度最小。这对减少起重小车的驱动功率，提高整机造型的和谐程度具有实际意义。

1 起重臂位移状态分析

1.1 单节臂架受力与位移的关系

对于平头式塔机起重臂，可将其力学模型简化为悬臂梁。当起重臂受自重载荷和起重载荷共同作用时，可将其受力情况转化为悬臂梁受均布自重载荷和集中起重载荷作用。设起重臂由n节臂架组成，选取任意一节臂架i（i=1，2，……，n）作为研究对象，分析其受力状态。第 节臂架的受力情况如图1所示，起重载荷作用于点A。均布自重载荷为qi，集中起重载荷为PQ，臂架长度为li。

图1 第i节臂受力情况

参照图1中的臂架受力情况可知，Pi为第i+1节臂架至第n节臂架的自重之和，Mi为分别将各节臂架的自重转移到第i节臂架的端部B处，相应产生的附加力矩之和，起重载荷PQ与臂架根部的距离为x（x∈［0，li］），梁的刚度为EI，则起重载荷作用点A处的垂直位移和转角位移分别为

式中的Pi和Mi取值如下

参照图1中的臂架受力情况，当起重载荷作用于A点时，求得第i节臂架的端部B处的垂直位移和转角位移分别为

起重载荷可以作用在任意一节起重臂臂架上的任意位置，端部集中载荷Pi和Mi以及起重载荷PQ都会有所不同，但载荷作用点和臂端位移计算方法不变。

上述的第i节臂架作用有起重载荷，第k节（k=1，2，…，≠i，i+1，i+2…，n）上没有作用起重载荷，第k节只有自重载荷和端部载荷作用，其端部载荷确定方法如下。

1）当k＞1时，

其中：j=k+1，k+2…，n-1；n为起重臂的节数。

2）当k＜i时，

则第k节端部的位移计算表达式如下

1.2 起重臂整体位移分析

前面分析了各节起重臂的位移状态，整个起重臂是由多节臂架组成的，并且处于根部的各节臂架位移都对处于端部的各节臂架的位姿有直接影响。以起重臂的前三节臂架AB、BC和CD为例（如图2所示），分析各节臂架在总体坐标下的垂直位移和转角位移。

图2 起重臂变形曲线

参照图2中的起重臂变形曲线可知，第一节臂架AB端部相对于臂根部有垂直位移Δ1，转角位移θ1；第二节臂架BC端部相对第一节臂架AB有垂直位移Δ2，转角位移θ2，则BC端部相对于起重臂臂根的垂直位移和转角位移分别为

根据变形曲线可知：Δh1=Δ1，y1=l2sinθ1，Δ2′=Δ2cosθ1

代入上式得两项位移如下

第三节臂架CD自身产生的垂直位移为Δ3，转角位移为θ3，则第三节臂架端部相对于起重臂臂根的垂直位移和转角位移分别为

根据变形曲线可知

代入上式得两项位移如下

由此可得任意第k节臂架端部相对起重臂臂根的两项位移均可以描述为

其中：k=1，2…，n。

起重载荷作用在第x节起重臂的点x处，则点相对臂根的两项位移可以描述为

其中：i=1，2…，n。

式（4）可以用来描述起重臂任意节端部的位移状态，而式（5）可以用来描述起重载荷在任意一点处的位移状态。

2 起重臂预翘度的研究

选取合理的预翘度既有利于塔机的整体造型，也有利于降低变幅降低驱动时的能耗。依据塔式起重机的起重特性，在超出额定最大起重量工作幅度后，不同的幅度具有不同的额定起重量。实际上塔机在日常工作时，任意幅度状态下施加的载荷是很难确定的，起重特性给定的只是额定载荷，在任意幅度施加任意载荷，起重臂各节都会产生与之相对应的位移，也就是垂直位移和转角位移，这些位移和转角均可以依据式（1）、（2）和（3）进行计算。

为了减少起重臂的下挠量，在起重臂设计时使其具有一定的上翘量，对下挠量进行一定程度的抵消。起重臂是杆系桁架结构，由于加工上的原因起重臂的上翘都是采用折线上翘的形式，即使起重臂在连接点处上翘一定的角度。其处理的方法就是使上弦杆的长度短于下弦杆，两节臂在连接点处就形成了一定角度的上翘。其上翘的角度可用如下方法分析计算。

设第k节起重臂末端上下弦杆长度差为δk，第k+1节与第k的连接处的上弦杆与下弦杆的长度差一般情况下也是δk，两者连接销轴间的距离为hk，得角度关系如图3所示。

图3 角度关系

参照如图3可得在连接处产生的预翘角θqk

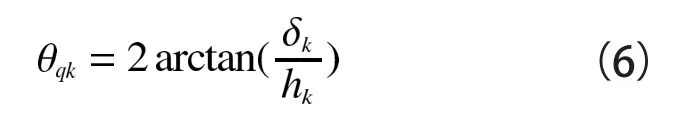
式（6）中关键的问题是如何确定起重臂末端上下弦杆长度差δk。如果δk确定了，则θqk就可以确定下来。

影响小车变幅阻力的实际上是起重载荷作用点的转角位移，而影响起重臂外观形态的是垂直位移变形，当然控制住了臂节端部的转角位移也可以控制起重臂的垂直位移量。尽管作用在起重臂上的载荷具有随意性，但塔机的起重特性曲线却规定了不同幅度状态下的额定起重载荷，不同幅度下的额定载荷也属于塔机正常状态下的极限载荷，这种载荷状态可以形成起重臂的最大位移值。依据式（4）和式（5）可以计算出各节臂端部的位移值和载荷作用点的位移值。依据起重特性曲线对起重臂进行全幅度加载，可以得出全部 节起重臂端部的极限位移值变化域，也就是极限垂直位移变化域和极限转角位移变化域，也就是由式（4）所计算结果的集合。还可以依据起重特性加载，得到沿全幅度变化的极限垂直位移变化值曲线和极限转角位移曲线，也就是式（5）沿全程所得最大值。

对于一般的平头式塔式起重机，起重臂的位移有两个因素产生，一是起重载荷使起重臂产生位移；二是自重载荷使起重臂产生位移。一般情况下起重载荷作用在第i节起重臂，考核第节起重臂臂端的位移。则第k节起重臂端部位移的两组参数域可以分别描述为［Δkmin， Δkmax］k≤i，［θkmin，θkmax］k≤i，其中，Δkmin和θkmin应该是k=i，且载荷作用点x=li时的取值，而Δkmax和θkmax应该出现在k与i差值最大的状态。即最大幅度的额定载荷在各节臂端产生的位移是最大位移，而载荷作用在本节臂臂端时产生的位移是最小位移。自重载荷在各节臂端产生的位移Δkq和θkq是恒值。

一般状态下Δkmax和θkmax都很难出现，可在介于两组参数域中，取一个当量常数值，并将其作为第k节起重臂的常态最大值，即

起重臂的预翘度要保证起重臂在工作状态和非工作状态下最大垂直位移量最小，但从垂直位移进行考核起重臂的预翘度难以控制，而臂端转角位移量实际上是与臂端垂直位移相对应的，而且小车运行阻力中包括爬坡阻力，取第k臂和第k+1节臂结合处形成的转角上翘的角θqk为

依据式（6）可得

δk分别为第k臂和第k+1节臂架接合处的上弦杆与下弦杆的长度差，也就是在这个接合处，两节臂架两侧的上弦杆比下弦杆分别短δk。

3 算例分析

现以PTT80（6010）型平头式塔式起重机起重臂为计算实例，研究起重臂的预翘度。起重臂整体为一个变截面结构，共由七节臂架组成，最大幅度为60m。

依据起重特性表可知，二倍率时平头塔式起重机在起重臂的最大幅度60m处起吊额定起重量1t时，在各节臂端部产生的转角位移为最大位移；而分别在各节臂的端部起吊相对应的额定起重量时，产生的转角位移为最小位移。

PTT80（6010）型平头式塔式起重机的吊钩重为1 920N，起重小车重为2 280N，二倍率起升钢丝绳重为700N，起重臂的臂头重为655N，臂头长度为0.289m，则各节臂架参数见表1。

依据表1中各节臂架的参数，结合二倍率起重特性表与式（1）、（2）和（3）即可求得当起重载荷作用时，各节臂端产生的最大转角位移θkmax和最小转角位移θkmin及当自重载荷作用时，各节臂端产生的θkq的值，将结果列于表2。

依据表2中所求得的数据，结合式（8）和（9）即可求得PTT80（6010）型平头式塔式起重机起重臂的各节臂架一侧的上下弦杆长度差值，并将结果列于表3。

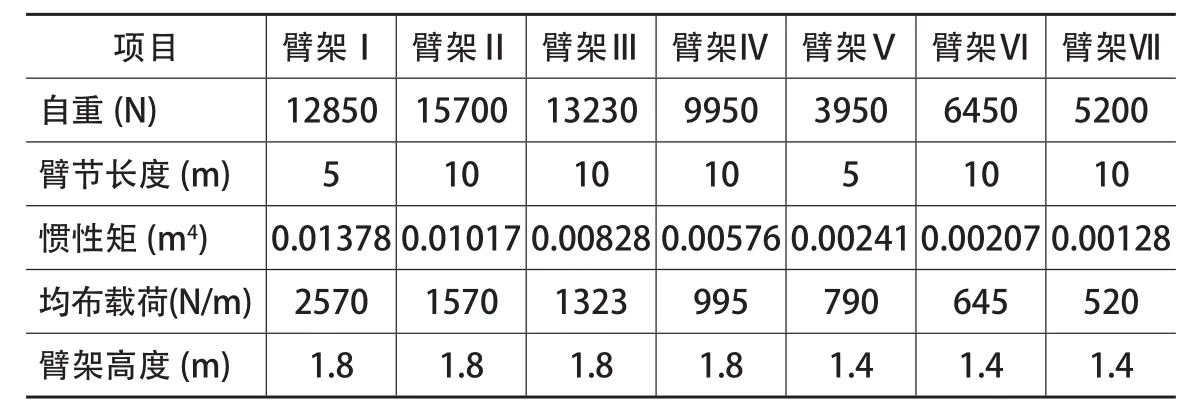
表1 臂架参数

表2 各节臂架转角

表3 上下弦杆一侧长度差

4 结 论

本文研究了平头式塔式起重机起重臂位移的计算方法，给出了在任意起重载荷作用下起重臂各节臂架端部的位移计算表达式和载荷作用点的位移计算表达式，分析了各节臂架端部的位移变化值域，确定了各节臂架接合处预翘角度的确定方法，并依据预翘角度给出了臂架接合处两侧上下弦杆应有的长度差。

［1］李廉锟.结构力学第5版［M］.北京：高等教育出版社，2011.

［2］袁尉卿，程海涛，赵 林.平头塔式起重机起重臂上翘量值探讨［J］.建设机械技术与管理，2014，（3）：87-89.

［3］郑奠一，杨 阳.塔机水平起重臂空载时上翘高度的确定［J］.建筑机械，1994，（1）：11-14.

［4］邹力生，王端秀.塔机小车起重臂端的预置起翘高度［J］.建筑机械化，1988，（10）：20-22.

（编辑 贾泽辉）

Research of hoist boom precast warpage design of the fl at type tower crane

LI Bin， LI Hong-qian

TH212；TH213.3

B

1001-1366（2015）08-0035-04

2015-05-09