基于PN的可重入医学检测调度系统优化研究

戴婉仪，张　梅*，胡跃明，陈广森

（1.华南理工大学自动化科学与工程学院，广州510641；2.精密电子制造装备教育部工程研究中心，广州510641）

基于PN的可重入医学检测调度系统优化研究

戴婉仪1，2，张梅1，2*，胡跃明1，2，陈广森1，2

（1.华南理工大学自动化科学与工程学院，广州510641；2.精密电子制造装备教育部工程研究中心，广州510641）

基于一类具有可重入特点的医学检测过程的设备调度问题，研究了具有约束条件的优化解.首先分析了调度约束条件和优化目标，建立了其Petri Networks（PN）形式化模型，并分析了其规则调度系统的稳定性和其他性能.然后利用PN模型和调度约束条件解出调度可行解结合对医学检测部分工序要求连续的基础上建立时间约束矩阵，对可行解进一步优化，最终得到满足所有约束条件的优化可行解.通过对实际医学检测系统的实例分析和CPN Tools仿真，结果表明所建立的模型和方法的有效性.

可重入系统；Petri网；医学检测；调度

可重入生产系统［1］有别于 Job-Shop和 Flow-Shop的第三类生产调度系统，由于具有可重入性特点，其调度过程更加复杂.目前可重入生产系统的调度研究主要集中在半导体、钢铁锻造等生产系统，已获得了较好的研究进展，并形成多种建模方法，如Kelly Networks模型、Queuing Networks模型、Brownian模型、Fluid Networks模型、Petri Networks模型和QBD模型等［2-10］.针对具有可重入特点的医学检测过程的调度问题研究甚少［11］.

本文所提出的可重入医学检测优化调度问题来源于实际医学检测过程.该问题可看成离散事件动态系统的优化问题，而PN模型是研究该类系统的重要建模工具，可较准确地描述调度过程的并发和并行等特性.本文在分析系统约束条件和优化目标的基础上，首先利用PN对调度问题进行建模研究，确定模型中库所的P集合和变迁T集合，借助它通过可达树和关联矩阵进行可重入医学检测调度优化系统稳定性及其他性能的分析和评价.并利用PN模型和约束条件得到一个可行调度方案，利用该可行调度方案与系统的时间约束矩阵相结合进一步获得更优的调度方案.

1　问题描述

图1为某医学生化指标检测过程，具有明显的可重入特性.整个检测过程将在全自动免疫分析检测设备上多次经过加样头、机械手、孵育振荡器、洗板机和分析仪等子模块而完成.当多个项目同时进行检测时，有效地调度这些资源将提高设备利用率，降低检测成本和提高检测时间周期.这类具有可重入性的优化调度问题是一类NP-hard优化调度问题［1］.

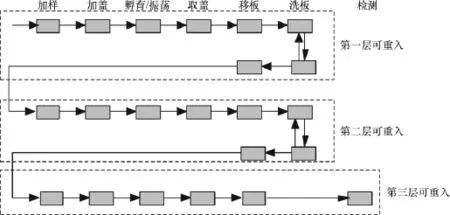
图1　某免疫检测项目可重入系统的工作流程图Figure 1　A medical and biochemical indicator testing process

一台检验设备中各子模块的个数可通过需求进行配备，子模块个数越多，可使用的检测资源越充足，但设备成本也将显著增大.因此，研究在一定数量的子模块下，建立调度优化模型，充分利用资源，降低检测成本，提高检测效率.

本文研究的调度系统检测设备子模块有5个，包括1个加样头、1个机械手、12个温育振荡器、2台洗板机、1台分析仪.把检验相同生化指标且放于同一检验板上的样本集合，定义为一个检验项目.每个检验项目均需经过若干检验步骤（称为工序）才能完成某项生化指标的检验.整个检测过程满足下列的基本约束:

①不同的检验项目间不存在优先级限制，且在零时刻所有的项目都可被检验；

②同一项目符合链式约束:同一检验项目l的工序必须按自然顺序；

③其中某些工序尽量满足连续性，最好无等待时间；

④设备使用的约束:对于某些设备不可同时使用，以免发生碰撞，但与其他设备可以同时进行，如加样头和机械手不能同时运动，以免相撞；

⑤设备资源是有限的；

⑥工序的不间断性:每台设备每个时刻只能执行一道工序，即某一道工序一旦在某设备上执行就不能中断直到该工序完成；

⑦每道工序的执行时间是固定的.

针对现有医学要求检验样本量大，为降低检测成本往往需要资源共享，要求一台检验设备同时进行多个项目的检测，而且要求在检验过程中以最小化最大完工时间为目标提高设备的工作效率，并且尽量减少检测误差，提高检验的准确性和检验过程的稳定性.因此，本文提出了该类医学检测过程的PN调度模型和求解调度方案的方法.

2　基于PN的建模与分析

为更清晰表述调度问题，定义如下的符号与变量:a表示需检验的项目数；Pl（l=1，2，…，a）表示单个的检验项目；Nl表示项目Pl的工序总数；k（k=1，2，…，Nl；l=1，2，…，a）表示各项目中的每一道工序；Plk表示第l个项目的第k道工序；表示第l个项目的第k道工序的固定执行时间；表示第l个项目的第k道工序的开始时间；表示第l个项目的第k道工序的完成时间；表示第l个项目的第k道工序的紧前工序集合；表示第l个项目的第k道工序与第k+1道工序的时间间隔；En表示第n类设备；AT表示在T时段内正在进行的项目及工序的集合；pi（i=1，2，…）表示库所；ρlk（k= 1，2，…）表示第l个检测项目的第k道工序变迁向量；ρT表示在T时段内工序变迁向量的集合.

针对调度系统以最小化最大完工时间为目标，目标函数表示为:

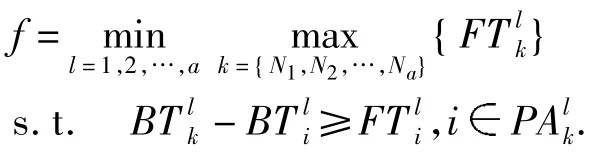
以某免疫检测项目（表1）为例进行PN建模.项目l=1，2，…，工序k=1，2，…，17，FTlk表示第l个项目的第k道工序的固定执行时间，单位为min，设备编号En（n=1，2，…，5；E1=加样头，E2=移板臂，E3=温育振荡器，E4=洗板机，E5=分析仪），用表示在工序进行中需要的设备号和执行时间.

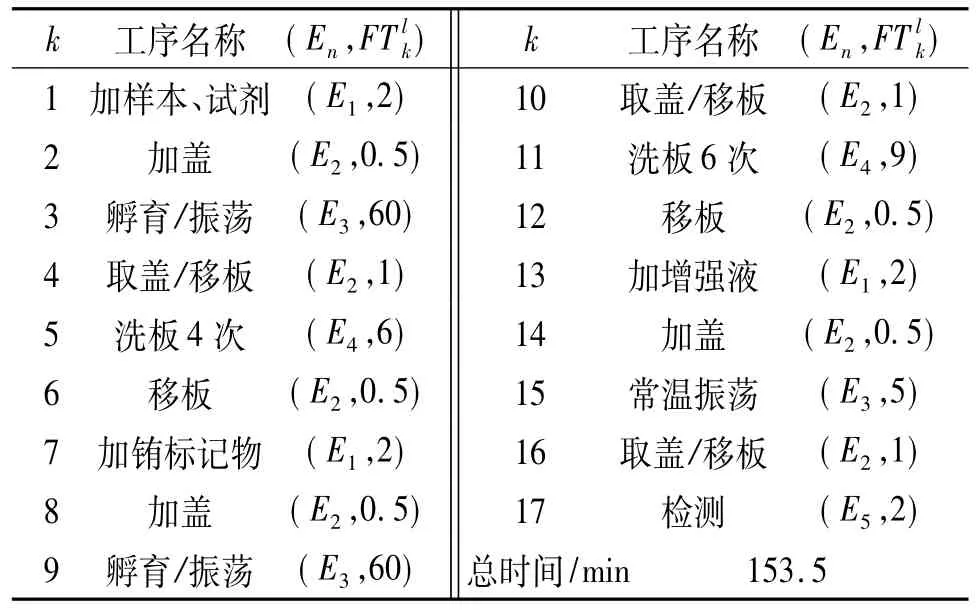
表1　某免疫检测项目工序过程及工序时间表Table 1　Testing process and its executing time for a biochemical indicator testing item

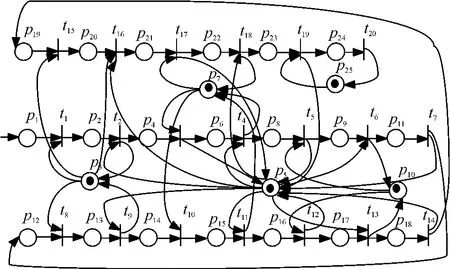
图2　可重入调度系统在FBFS下的PN模型Figure 2　PN model for reentrant scheduling system according to FBFS

为了建立该调度过程的PN模型，在每次可重入检测过程时，设立了3个虚拟缓冲区，待检验的样本将在缓冲区内等待资源进行下一步检测.可重入调度中的工序、设备状态等用库所表示，工序开始或结束用变迁来表示，图1所示的检测过程PN模型如图2所示，其中p1，p12，p19为虚拟的缓冲区库所，p3，p5，p7，p10，p25为设备组库所，其余的pi为正在进行的工序库所，而ti（i=1，2，…，20）表示工序开始或结束的变迁.在缓冲区p1中存在一定量的待检测的项目，可以允许有新项目的进入，（k=1，2，…，Nl；l=1，2，…，a）已知.为考虑缓冲区的优先级，项目开始时按调度规则FBFS（First Buffer First Served）进行，同时由于洗板机数量较少且工序执行时间相对较长，在调度过程中应优先对其进行调度.在明确了调度规则后，对系统的稳定性进行分析是十分必要的.

2.1调度的稳定性分析

根据文献［2］，生产系统的稳定性解释为:（1）缓冲区中的工件数目是有限的；（2）进入生产系统的工件在有限的时间内可以离开.基于图2所示的PN模型，得到它的关联矩阵

这里的行标代表25个库所，列标代表20个变迁，其中

设x=（x1，x2，x3，…，x24，x25）T，求解线性方程组xTA=0.由于Rank（A）=20，可得S-不变量［5］含有5个自由未知量λi（i=1，2，…，5），满足x，其中ξi（i=1，2，…，5）为基础解系.从 ξi（i=1，2，…，5）中发现，其各分量反映了5个设备在工序中的使用情况（ξi中的1表示第i种设备在该工序中被用，0表示不被用）和设备库所.如ξ1表示为:ξ1=（0，1，1，0，0，0，0，0，0，0，0，0，1，0，0，0，0，0，0，1，0，0，0，0，0）T；因而x可表示为

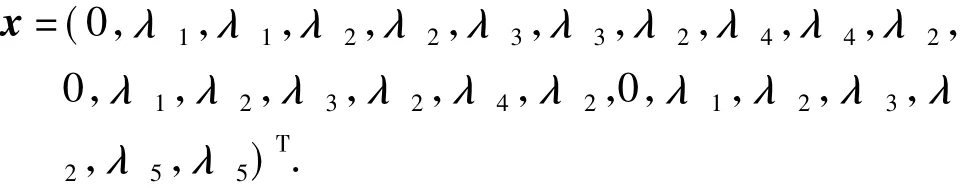
注意到在x中各分量，去除第1、12和19是3个缓冲区库所的位置和第3、5、7、10、25的设备的库所位置，剩下的各分量下标的顺序就是检验过程中设备的使用顺序.根据实际的意义，λi（i=1，2，…，5）应满足λ1≤1，λ2≤1，λ3≤12，λ4≤2，λ5≤1.根据S-不变量的性质［5］，还应满足:

其中，φ=（a1，a2，…，a25）T，ai（i=1，2，…，25）为库所pi（i=1，2，…，25）中的令牌数；φ0为最初的各库所的令牌数，即φ0=（a，0，1，0，1，0，12，0，0，2，0，0，0，0，0，0，0，0，0，0，0，0，0，0，1）T，这里a是要检测的项目数，允许进来新的检测项目.根据式（1）可得

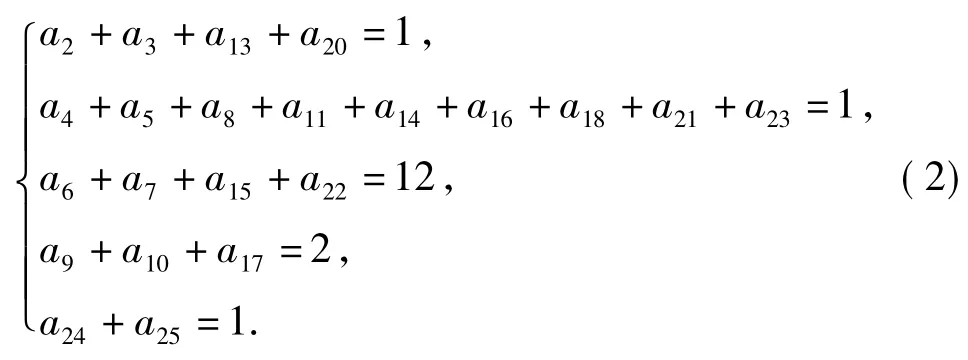
解式（2）得到

其中ki≥0（i=1，2，…，25），但根据检测项目的实际意义，ki（i=1，2，…，25）的取值应该满足下列的条件:k2，k3，k5，k7，k9，k10，k12，k14，k16，k17，k19，k20= 0，1；k4，k11，k18=0，1，…，12；k6，k13=0，1，2；由此可见，库所p2，p3，p4，p5，p6，p7，p9，p10，p11，p12，p13，p14， p16，p17，p18，p19，p20中的令牌数有界，而k1，k8，k15是缓冲区库所的令牌数，令k=max｛k1，k8，k15｝，故所有库所的令牌数有限，则PN是有界的.也就是说在FBFS调度规则下，图2所示的可重入式的调度问题是稳定的.

2.2在调度规则下，性能指标与模型参数的关系分析

在整个调度过程中，pi（i=2，…，25）中的令牌数变化可以通过PN的可达树来描述.令［ti，δi］（i=1，2，…，20），其中ti为当前被激发的变迁，δi为变迁ti发生所需的时间，也即当前工序的执行时间.变迁的过程即PN的可达树如图3所示，变迁中的第一个分量*代表检验项目的来源情况.

图3　PN可达树Figure 3　Reachability tree of Petri Net

图3的变迁时间表明时间间隔最小为0.5 min，于是把每类设备用时间按0.5 min的标准分割成一些点集.在同一个时间间隔［t，t+0.5］，必须满足下述不等式:

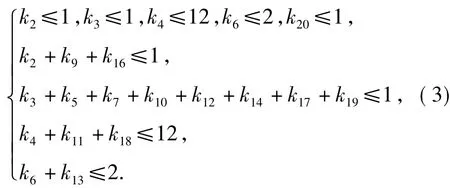
由于加样头和机械手采用一条导轨运动，所以还应该满足

如果把每一次的变迁用ρlk表示，其中缓冲区库所的令牌数和设备库所令牌数都用*代替.如使用E2的变迁包含:

其他设备的使用变迁类似.这些变迁在任意［t，t+ 0.5］时间段里，应满足:

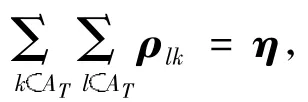
其中η=［*，t1，*，t2，*，t3，*，t4，t5，*，t6，*，t7，t8，t9，t10，t11，t12，*，t13，t14，t15，t16，t17，*］，且满足:t1+t2+t4+t6+t7+t8+t10+t12+t13+ t14+t16≤1；t3+t9+t15≤12；t5+t11≤2；t17≤1.

根据队列理论，把每一次的新进项目看成是队列的入队.项目检查完毕就是队列的出队.队列遵循先进先出原则，因此，此检测过程的工序的调度可看成队列排序，以队列理论可求出调度可行解.

3　实例分析

对表1的数据进行实例分析，根据PN模型图2，检测开始时项目在缓冲区处于等待状态，所有的设备都可使用.从表1知最小的工序执行时间是0.5 min，因此以［t，t+0.5］时间区间对检测过程进行划分，在每个［t，t+0.5］时间区间中调度需满足式（3）和式（4）的约束关系.假设有a个项目待检测，即项目l（l=1，2，…，a）的工序分别表示为Pl1，Pl2，…，Pl，17（l=1，2，…，a）.由于各检测项目具有链式约束，即满足式（5）:

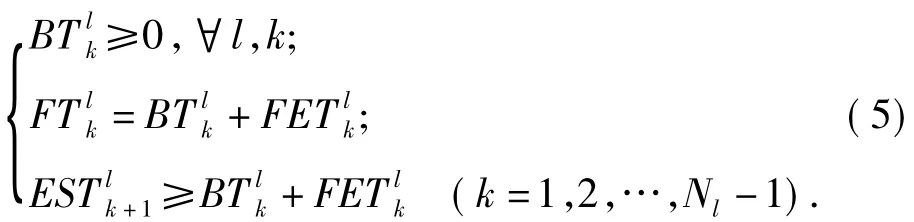
依据式（5）可得到一个满足链式约束的调度方案Pα11，Pα2β1，…，Pα3β2，Pα4，17，其中:若 α1=α2，则 β1=2；若α1≠α2，则β1=1；若α2=α3，则β1＜β2；若α3=α4，则β2=16；α3≠α4，则β2=17.而αi=1，2，…，a；βj=1，2，…，17.由此可见调度的可行解个数将出现组合爆炸，该调度问题是一个NP难问题.本文根据问题约束条件建立时间约束矩阵，将寻求最小完工时间问题变为最小化时间约束矩阵问题，利用易于求解的最小化时间约束矩阵求出最优检测过程调度方案.具体的算法及过程如下:

（1）首先根据约束式（3）和式（4）寻找一组调度可行解.

由于洗板机数量较少且工序执行时间相对较长，在调度过程中应优先考虑对其进行调度.加上检验项目的精确性要求，需在孵育工序后尽快进行洗板工序，即（k=3，…，5，9，…，11，15，16）尽量小.由于加样头和机械手采用一条导轨运动，假如首先P1进入调度队列，根据链式约束在完成P11和P12，即在［0，3］时间区间后，才可插入新的成员.若此时在［3，3.5］加入新成员P2，后续寻解过程如下:

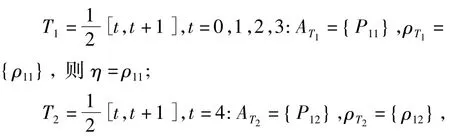
则η=ρ12；

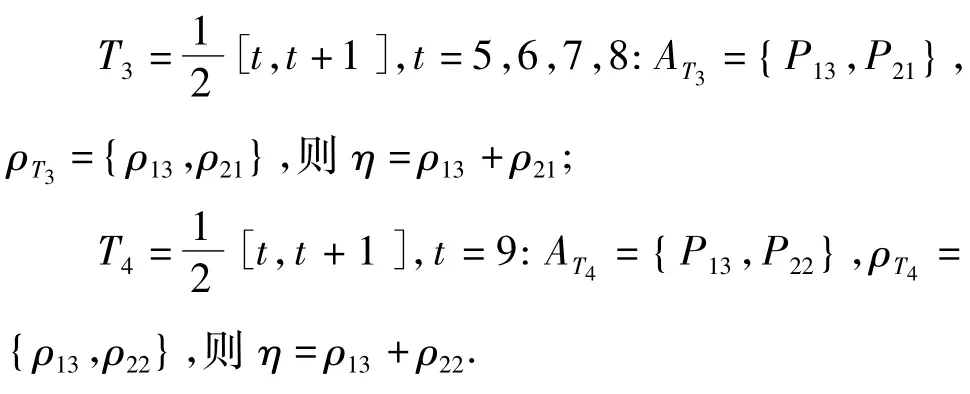
根据上述寻解过程及式（3）～（5）的调度约束条件，可以得到同时进行12个检测项目的工序开始时间向量yl（l=1，2，…，12）为:

y1=［0，2，2.5，62.5，63.5，69.5，70.5，73，73.5，133.5，134.5，143.5，144，146，146.5，152.5，153.5］；

y2=［2.5，4.5，5，65，66，72.5，74.5，78，78.5，138.5，139.5，148.5，150，152，152.5，162，163］；

y3=［5，7，7.5，67.5，70.5，76.5，78.5，82，82.5，146.5，147.5，156.5，158，162.5，163，168.5，169.5］；

y4=［7.5，9.5，10，73.5，74.5，80.5，82.5，86，86.5，149，150，160，163.5，163.5，167，173，174］；

y5=［10，12，12.5，77，78，84.5，86.5，90，90.5，157，158，167，169.5，176.5，177，183.5，184.5］；

y6=［12.5，14.5，15，81，82，88.5，90.5，94，94.5，160.5，161.5，171，174，179，179.5，187，188］；

y7=［15，17，17.5，85，86，92.5，94.5，98，99，167.5，168.5，177.5，179.5，184.5，185，190，191］；

y8=［17.5，19.5，20，89，90，96.5，99，102，102.5，172，173，182，185，189.5，190，195，196］；

y9=［20，22，22.5，93，94，100.5，104.5，106.5，107.5，178，179，188，191，194.5，195，201，202］；

y10=［22.5，24.5，25，97，98，104，107，109，109.5，182.5，183.5，193，196，198，198.5，203.5，204.5］；

y11=［25，27，27.5，101，102，109.5，110，112，112.5，188.5，189.5，198.5，199，202，202.5，208，209］；

y12=［27.5，29.5，30，104，105，112.5，113，115，115.5，193.5，194.5，204.5，205，207，207.5，213，214］.

则完成12个检验项目总时间是216 min.相比于12个项目按顺序完成（需要的时间是1 842 min）在效率上提高了8.5倍多，可见建立的调度方案具有较好的时间优越性，但不代表是较好的可行调度解，因此需要对其进行可行解的进一步分析.

（2）可行解的进一步优化和调整.

如果只做一个检测项目，根据工序的链式约束及工序工作时间，可得该项目的工序开始时间向量为y0=［0，2，2.5，62.5，63.5，69.5，70，72，72.5，132.5，133.5，142.5，143，145，145.5，150.5， 151.5］，则=0（k=1，2，…，16）是最理想的检验状态.12个检验项目的可行调度方案与它的图形用图4表示，可见每条项目检测曲线与理想检测曲线是基本相似的.

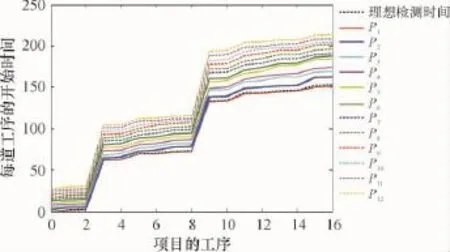
图4　12个检测项目时间与理想检测时间曲线图Figure 4　Process time of 12 testing items and idea testing time

下面讨论所得到的12个调度方案与理想状态的差异.令:

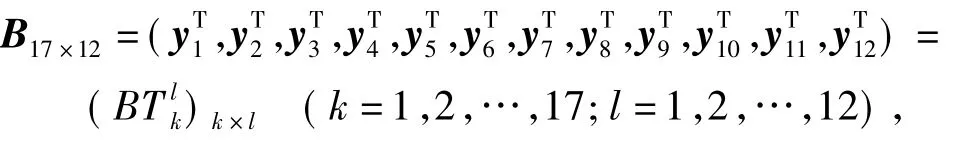
称为项目工序开始时间矩阵.

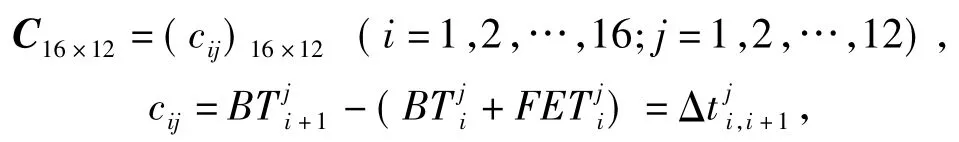
称C为各项目工序检测等待时间矩阵.根据检验项目的精确性要求，需在孵育工序后尽快进行洗板工序，即（k=3，4，5；9，10，11；15，16）尽量小.特别地，若C满足，，则记为C*，称为工序时间约束矩阵.所以所有得到的可行调度方案，不仅在时间上要提高效率，也要在时间约束上满足时间约束矩阵的要求.根据矩阵 B可以得到相应的矩阵 C，其中.再计算.发现P2，P5，…，P12都不满足时间约束的要求，所以根据所得矩阵C在时间上作调整，寻求更优解.步骤如下:

（1）根据最初矩阵C，对工序开始时间调整，满足:

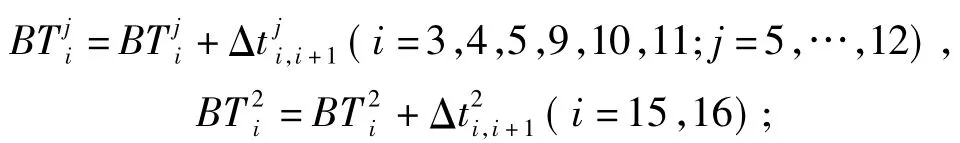
（2）重新得到一个新的项目工序开始时间矩阵B1；

（3）重新计算得到一个新的矩阵C，并与C*做比较；

（4）判断是否满足，否者重复从第（1）步开始.经过计算都满足了C*的要求，说明全部项目的检验时间都满足检验的时间约束.调整后的时间需验证各时间段是否满足η检验过程要求.因此，可以考虑对所有的工序开始时间进行排列，得到按一个满足约束关系含有204个数据的调度方案 Pα11，Pα2β1，…，Pα3β2，Pα4，17进行分析.根据数据排列，用MATLAB软件可以找回每一个时间点相应项目工序.如利用［i，j］=find（U=5），可找5的位置是P32和P13，这样下去，就可以列出所有工序的排列情况，再利用前面的队列和ρlk（l=1，2，…，12；k=1，2，…，17），可以验证调度方案是可行的，且此时得到的调度方案同时在工作效率和满足连续性上都达到了实际的要求.

3）模型的仿真分析.针对上述的12个相同的项目的研究，用CPN Tools进行模型仿真（图5）.

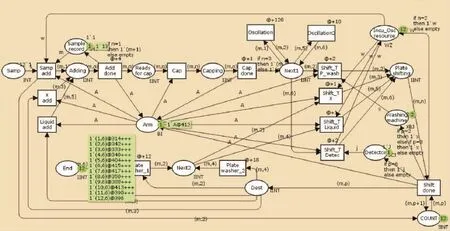
图5　CPN Tools的仿真截图Figure 5　Simulation of CPN Tools screenshot

因为里面的仿真时间只能为整数仿真，所以模型里面的所有变迁时间全部加倍，因此实际的总花费时间为仿真时间的一半.每次经过336步的多次仿真结果显示，最好的总的工序时间为206.5 min.这个运行结果与通过PN模型得出的结果几乎是一致的，总的时间减少了9.5 min，这说明PN模型建立的有效性.

4　结束语

本文对一类可重入的医学检测过程建立了Petri网模型，利用其关联矩阵和可达树分析了模型的稳定性态及其他性能.根据PN模型和约束条件，找到一个在工作效率上提高了8.5倍多的可行调度方案，再通过时间约束矩阵的要求，调整某些工序的开始执行时间，最终得到较优的调度方案，且利用MATLAB软件验证所得到的调度方案满足了问题的约束要求，最后，利用CPN Tools进行模型仿真，结果显示总的工序时间几乎是一致的.本文的研究结果在一定程度上扩充了可重入调度研究问题的领域，符合医学的实际生化免疫检测的需要.为了适合实际的免疫检测，对不同工序的不同检测项目的建模分析，仍需要进行进一步的理论研究和探讨.

［1］Kumar P R.Re-entrant lines［J］.Queuing Systems，1993，13（1-2）:87-110.

［2］Lu S H，Kumar P R.Distributed scheduling based on due dates and buffer priorities［J］.IEEE Transaction on Automatic Control，1991，36（12）:1406-1416.

［3］Zhou M C，Jeng M D.Modeling，analysis，simulation，scheduling，and control of semiconductor manufacturing system:A Petri Net approach［J］.IEEE Transaction on Semiconductor Manufacturing，1998，11（3）:333-357.

［4］Lin M H，Fu L C.Modeling，analysis，simulation，scheduling，and control of semiconductor manufacturing system:A generalized stochastic colored timed Petri Net approach，systems，man，and cybe-rnetics［J］.IEEE SMC’99 Conference Proceeding，1999（3）:769-774.

［5］任艳频，张佐，吴秋峰.一类规则调度系统的Petri网研究方法［J］.计算机集成制造，1999，5（2）:58-61. Ren Y P，Zhang Z，Wu Q F.Research on a class of rulebased scheduling system using Petri net［J］.Computer Integrate Manufacturing Systems，1999，5（2）:58-61.

［6］吕文彦.党延忠.基于Petri网与遗传算法的可重入生产系统调度［J］.计算机工程与应用，2005，19:226-228；232. Lv W Y，Dang Y Z.Scheduling reentrant lines based on Petri Net and GA［J］.Computer Engineering and Applications，2005，19:226-228；232.

［7］赵丽娜.可重入生产系统的调度优化与性能分析［D］.北京:中国科学院自动化研究所，1999. Zhao L N.Scheduling optimization and performance analysis of reentrant lines［M］.Beijing:Institute of Automation Chinese Academy of Sciences，1999.

［8］ 郑应平，赵丽娜，王利存.可重入生产系统的QBD型模型［J］.自动化学报，2001，27（5）:593-605. Zheng Y P，Zhao L N，Wang L C.Quasi-birth-and-death type models of reentrant lines［J］.Acta Automatica Sinica，2001，27（5）:593-605

［9］陈晓慧，张启忠.可重入式生产车间调度的计算机仿真与优化研究［J］.计算机科学，2009，36（9）:297-299；302. Chen X H，Zhang Q Z.Production scheduling simulation and optimization of reentrant produce jop shop［J］.Computer Science，2009，36（9）:297-299；302.

［10］钱省三，郭永辉.多重入芯片复杂制造系统生产优化与控制［M］.北京:电子工业出版社，2008:1-130.

［11］高臣杰，张梅，胡跃明.基于改进的遗传算法的链式约束排序问题的研究［EB/OL］.（2011-12-23）［2014 -03-12］.北京:中国科技论文在线，http://www.paper.edu.cn/html/releasepaper/2011/12/680/. Gao C J，Zhang M，Hu Y M.Research of sequencing with chain constraints based on improved genetic algorithm［EB/OL］.（2011-12-23）［2014-03-12］.Bei Jing: Sciencepaper Online，http://www.paper.edu.cn/html/ releasepaper/2011/12/680/.

【中文责编：庄晓琼英文责编：肖菁】

Research on PN-Based Scheduling Optimization for Reentrant Medical Testing System

Dai Wanyi1，2，Zhang Mei1，2*，Hu Yueming1，2，Chen Guangsen1，2
（1.College of Automatic Science and Engineering，South China University of Technology，Guangzhou 510641，China；2.Engineering Research Centre for Precision Electronic Manufacturing Equipments of Ministry of Education，Guangzhou 510641，China）

The optimal solution to the scheduling problem to reentrant medical devices testing process for the constraint conditions is studied.Firstly，a formal Petri Net（PN）model is built by analysis of scheduling constraints，optimization objectives，system stability and other system properties.Furthermore，based on the PN model and its scheduling constraints，a feasible scheduling solution is calculated.It combines with continuous recycling constraint of medical test and established time constraint matrix.The feasible solution is eventually optimized.Finally，the practical analysis of medical testing systems and CPN Tools simulation method turn out the result for the established models and methods are valid.

reentrant system；Petri net；medical testing；scheduling

TP301

A

1000-5463（2015）03-0151-08

2014-07-10《华南师范大学学报（自然科学版）》网址:http://journal.scnu.edu.cn/n

广东省产学研重点项目（2011A090200047）；广州市科技重大专项计划-产学研专项（2012Y5-00004）；中央高校基本科研业务费专项资金资助（2014zz0033）

张梅，副教授，Email:zhangmei@scut.edu.cn.