弱耦合三种群反应扩散模型的全局渐近稳定性

吴楚芬

（佛山科学技术学院信息科学与数学系，佛山528000）

弱耦合三种群反应扩散模型的全局渐近稳定性

吴楚芬*

（佛山科学技术学院信息科学与数学系，佛山528000）

近年来，随着入侵种的增加，多种群的反应扩散模型开始应用于入侵生态理论的研究.多种群的反应扩散模型可将空间、种群间相互作用过程融合进入侵速率的预测之中，且模型中连续参数的使用不受尺度限制，适用空间尺度较广.该文研究了一类非线性三种群弱耦合食饵-捕食者反应扩散模型的初边值问题，通过构造合适的常数上下解以及相应的迭代方式，得到了该系统在齐次Neumann边值条件下平凡解和非负半平凡解的全局渐近稳定性的充分性条件.所得结果揭示了通过控制种群自身的出生率、种间、种内相互作用率来达到某些种群消失、某些种群持续生存的现象.这些稳定性条件易于验证且与扩散系数无关，因此，该结论也适用于某个di=0或所有di=0的相应的抛物-常微分系统.

三种群；反应扩散系统；非负半平凡解；全局渐近稳定性

生物入侵的机理与控制是当前生态学关注的重点和研究的热点问题.外来物种由于自然因素或人为原因被引入新的生境，随后建群、扩散并入侵本土物种，造成本地物种绝灭、生物多样性丧失.基于数学生物学的角度，构建合适的数学模型，对模型进行定性与定量的分析，不仅有助于解释自然界的一些复杂现象，发现入侵问题的机制，而且有利于实现生态入侵过程中的预测与控制［1］.近年来，随着入侵种的增加，多种群的反应扩散模型开始应用于入侵生态理论的研究.这些模型可将空间因素、种群间相互作用过程结合进简单的预测框架，并对个体模拟元素的空间位置进行跟踪，使模型的预测可与地域联系起来进行更深入的研究［2］.为了模拟2类外来物种入侵本地物种，Kim与Lin［3］提出了一类非线性三种群弱耦合食饵——捕食者反应扩散模型:

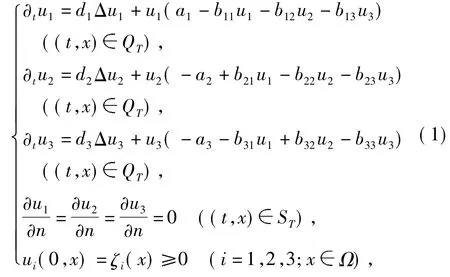
其中QT=（0，T）×Ω，ST=（0，T）×∂Ω，0＜T≤+∞，Ω为N中的有界区域，其边界∂Ω光滑，∂/∂n为边界∂Ω上的单位外法向量.在系统（1）中，ui（t，x）表示在t时刻处于x位置第i个种群的空间密度，di≥0表示第i个种群的扩散速率，ai＞0表示第i个种群的内禀增长率或死亡率，bii表示种内竞争系数，b12、b21表示种群1、2之间的捕食关系，b23、b32表示种群2、3之间的捕食关系，b13、b31表示种群1、3之间的竞争系数，bij≥0（i，j=1，2，3）.齐次Neumann边值条件指3类种群在边界上没有迁移.在系统（1）中，种群2与种群3为入侵种，种群3是比种群2更具有竞争优势的外来物种，它捕食种群2但与种群1竞争当地生态资源；种群2捕食种群1.

若b13=0、b31=0且考虑时滞对种群动力学行为的影响，则系统（1）变为:

2004年，林支桂［4］应用上下解方法结合迭代技巧，研究了系统（2）解的渐近行为；Chen与Wang［5］通过改造上下解，减弱对初始函数的限制，得到了类似的结论.2007年，Wang［6］进一步构造新的上下解，完整地得到了系统（2）在不同参数下解的渐近行为.对于完整系统（1），即bij＞0（i，j=1，2，3），Kim与Lin［3］利用Harnack不等式、解的先验估计结合Liapunov函数法研究了其正平衡态的存在唯一性.但关于完整系统（1）其平凡解（0，0，0）和非负半平凡解的全局渐近性态，据作者所知，尚未有文献报道.其实，随着自然界资源被过度开发以及外来物种的入侵，越来越多的物种走向灭绝，而稳定的平凡解（0，0，0）或稳定的非负半平凡解对应的生态学含义恰恰表示所有种群或某些种群最终绝灭.

本文利用构造合适的常数上下解以及结合混拟单调抛物系统解的一般理论［7］，研究完整系统（1）在不同参数下平凡解和非负半平凡解的全局渐近稳定性条件，进而提供调控生物入侵的若干数学理论依据.这些稳定性条件与扩散系数无关，因此，本文的结论也适用于某个di=0或所有di=0的相应的抛物-常微分系统.

1　预备知识

下设bij＞0（i，j=1，2，3）.显然，系统（1）与下述系统等价:

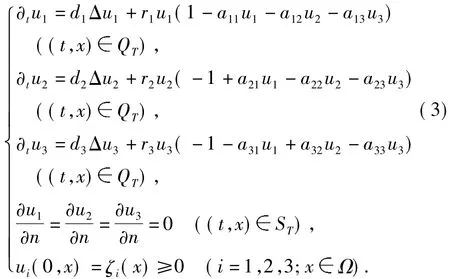
令w1=a11u1，w2=a12u2，w3=a13u3，则系统（3）可化为:

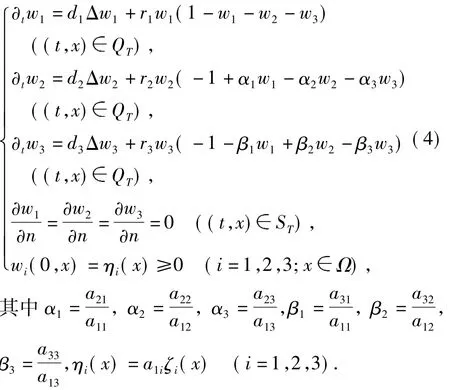
则系统（4）存在一个正平衡态（w*1，w*2，w*3），其中

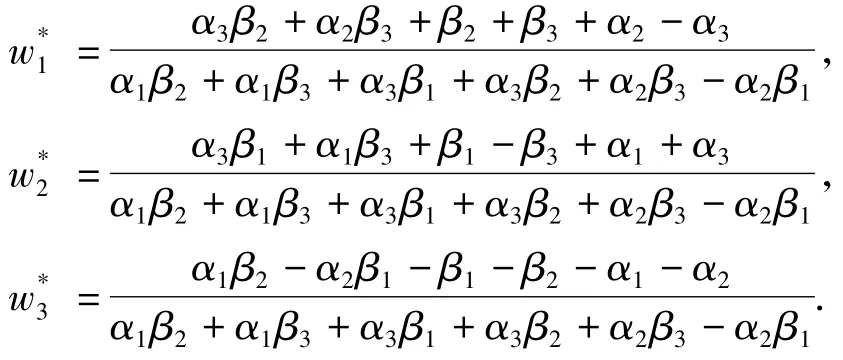
为简单起见，令

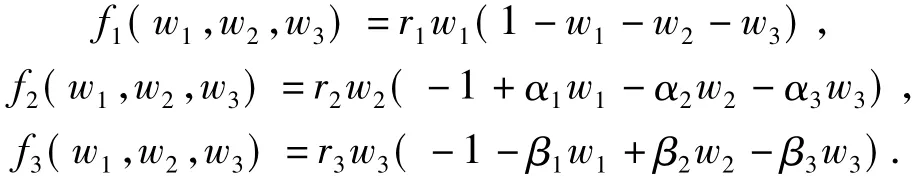
首先引入系统（4）上下解的定义:

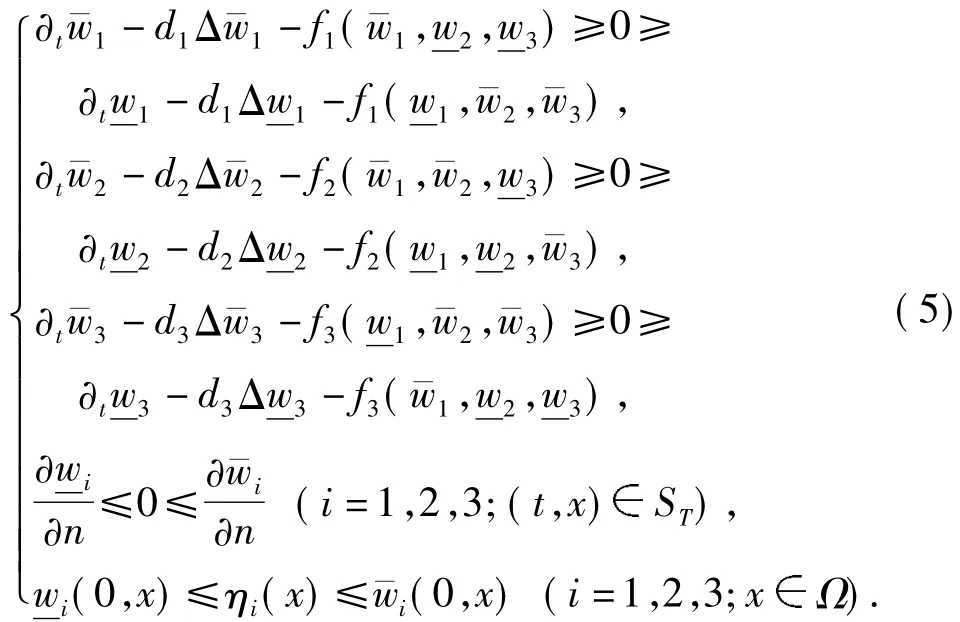
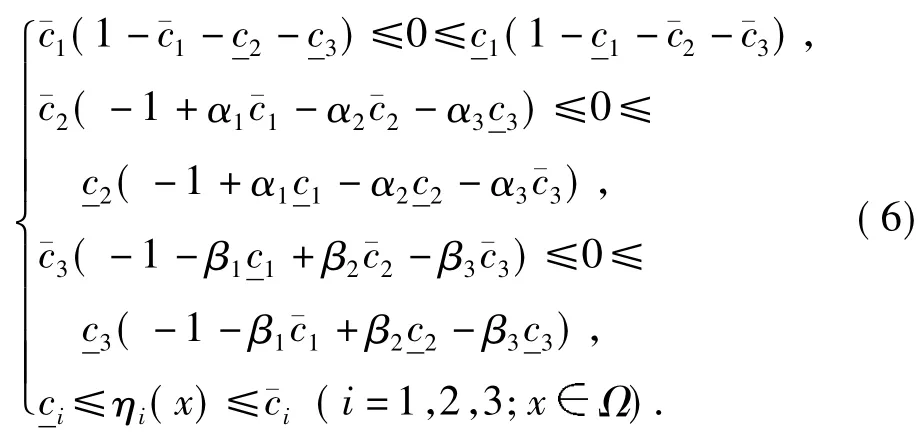
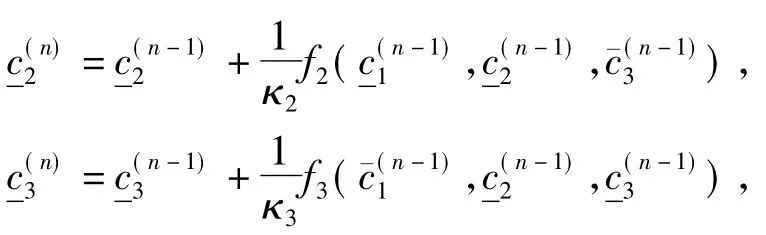
其中κ1=r1（21+2+3），κ2=r2（1+2α22+α33）及κ3=r3（1+β11+2β33）.根据文献［7］的定理

4.2，易证如下3个引理:

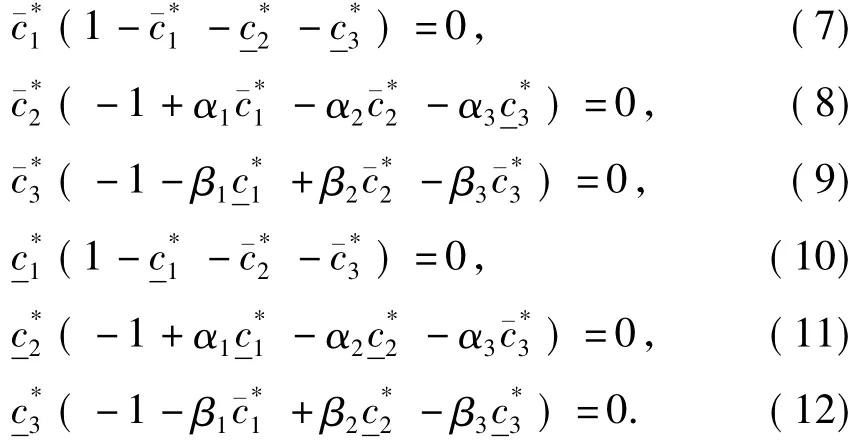
引理3设引理2的条件满足，w（t，x）为系统（4）相应于任一非负初值函数η（x）的一个解.若 c*=*且存在t0≥0使得，则limt→∞w（t，x）=c¯*在Ω一致成立.

下述定理表明系统（1）解的最大存在区间T= +∞.

定理1对于任意非负的初值函数（η1，η2，η3），系统（4）存在唯一的全局解（w1，w2，w3）满足0≤wi（t，x）≤Mi，对所有的（t，x）［0，∞）×成立，其中（i=1，2，3），m1=1， m2=α1/α2，m3=（α1β2）/（α2β3）.

证明注意到正常向量（M1，M2，M3）和零向量（0，0，0）为系统（4）的一对耦合上下解.由引理1，结论成立.证毕.□

2　主要结果

定理2设（w1（t，x），w2（t，x），w3（t，x））为系统（4）相应于任一非负初值函数（η1（x），η2（x），η3（x））的唯一解，则如下结论成立:

（a）若η1（x）≡0，，则当t→∞时，有（w1（t，x），w2（t，x），w3（t，x））→（0，0，0）在一致成立.

（b）若η2（x）≡0，η1（x）≢0，∀x，则当t→∞时，有（w1（t，x），w2（t，x），w3（t，x））→（1，0，0）在一致成立.

（c）若η3（x）≡0，η1（x）≢0，η2（x）≢0，∀x且α1≤1，则当t→∞时，恒有（w1（t，x），w2（t，x），w3（t，x））→（1，0，0）在一致成立.

（d）若η1（x）≢0，η2（x）≢0，η3（x）≢0，∀x且α1≤1，则当t→∞时，恒有（w1（t，x），w2（t，x），w3（t，x））→（1，0，0）在一致成立.

（e）若η3（x）≡0，η1（x）≢0，η2（x）≢0，∀x且α2＞α1＞1，则当t→∞时，有（w1（t，x），w2（t，x），w3（t，x））→在一致成立.

（f）若η1（x）≢0，η2（x）≢0，η3（x）≢0，∀x，α2＞α1＞1且α2+β2＞α1β2，则当t→∞时，有（w1（t，x），w2（t，x），w3（t，x））→0）在一致成立.

（g）若η1（x）≢0，η2（x）≢0，η3（x）≢0，∀x，α1＞1，α2+β2≤α1β2≤α2β1+α1+β1+α2+β2且α2（β3-β1）＞α1（β3+β2）+α3（β1+β2），则当t→∞时，有（w1（t，x），w2（t，x），w3（t，x））→，0）在一致成立.

证明（a）若η1（x）≡0，∀xΩ，则由解的存在唯一性，知w1（t，x）≡0，∀（t，x）（0，∞）×Ω.此时，系统（4）可约化为，则易证（ρe-γt，ρe-γtβ2/β3）和（0，0）为系统（4）的一对耦合上下解.由引理1，有（0，0）≤（w2（t，x），w3（t，x））≤（ρe-γt，ρe-γtβ2/β3）.令t→∞，则（w1（t，x），w2（t，x），w3（t，x））→（0，0， 0）在一致成立.

记γ=min｛r2，r3｝及

（b）若η2（x）≡0，∀x，则w2（t，x）≡0，∀（t，x）（0，∞）×Ω.另一方面，η1（x）≢0，∀x，由强极值原理知w1（t，x）＞0，∀（t，x）（0，∞）×Ω.故系统（4）可约化为

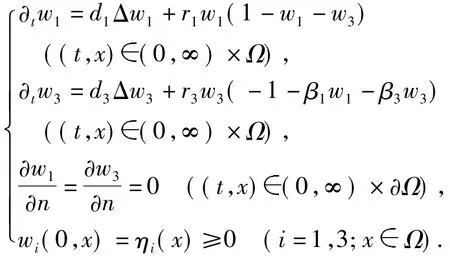
由比较原理，有

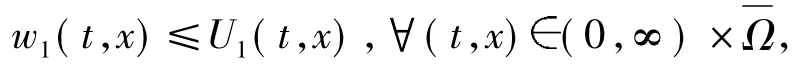
其中U1满足下述初边值问题

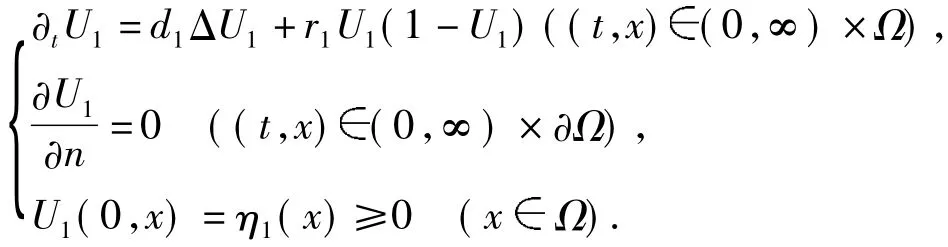
由于η1（x）≢0，∀x，故当t→∞时，有U1（t，x）→1.因此，对∀ε1＞0，存在t1＞0，使得w1（t，x）≤1+ε1，∀（t，x）［t1，∞）×.

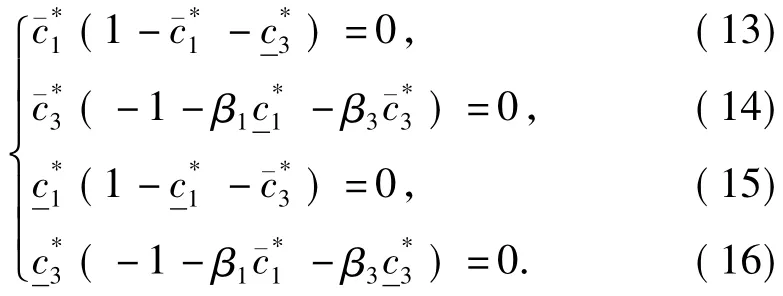
及

（c）证明过程与情形（b）类似，故省略之.

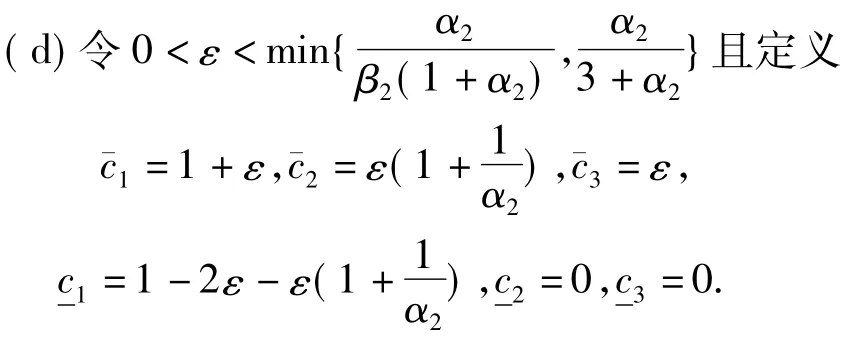
注意到α1≤1，知

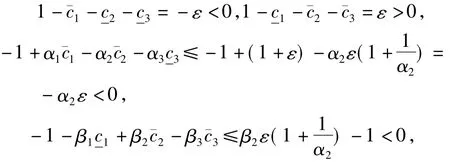
故式（6）成立.由情形（b）的证明过程，知存在t1＞ 0使得

由上述估计式且注意到α1≤1，有

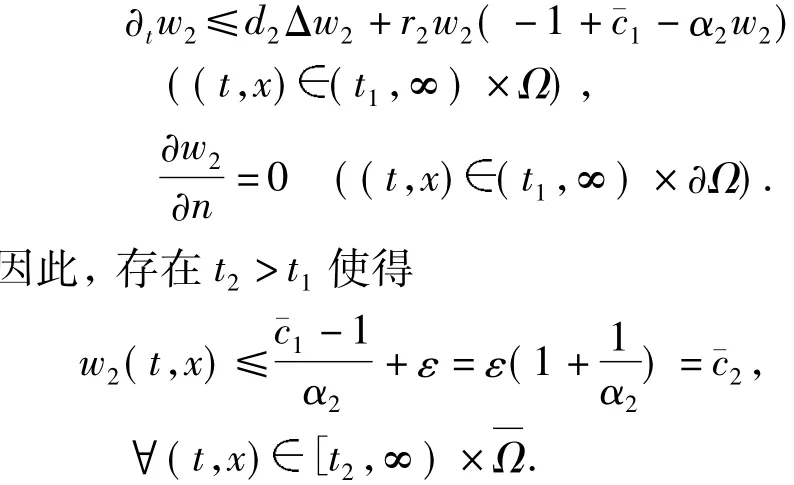
将上述估计式应用到系统（4）的第3个方程，有

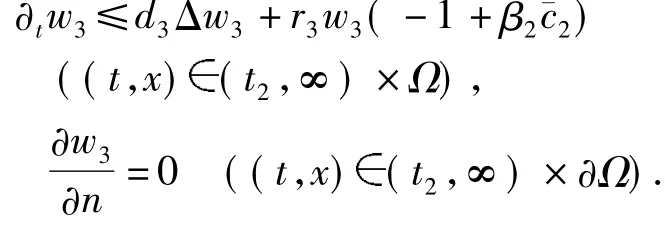
由于-1+β22＜0，故存在t3＞t2使得

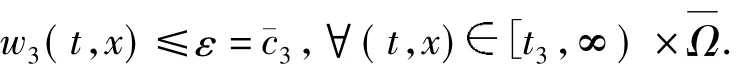
将w2，w3的估计式应用到系统（4）的第1个方程，有

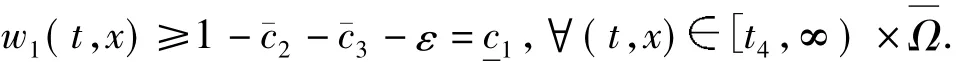
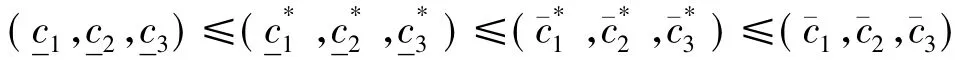
（e）证明过程与情形（d）类似，故省略之.

（f）令

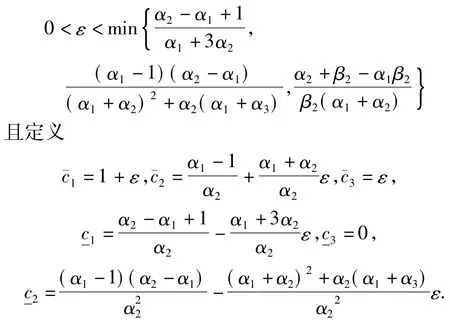
易证式（6）成立.类似于情形（d）的证明过程，知存在t5＞0使得

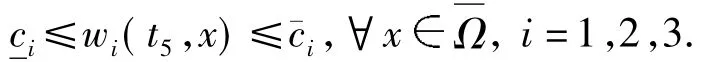
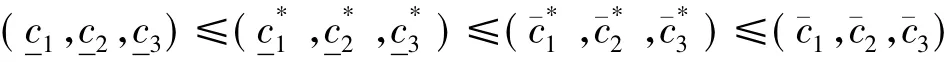
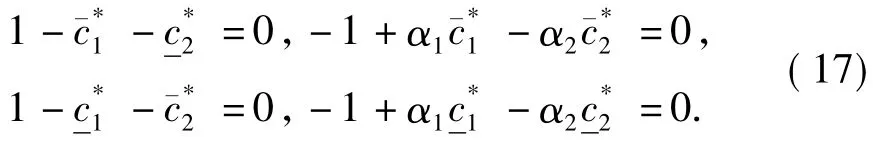
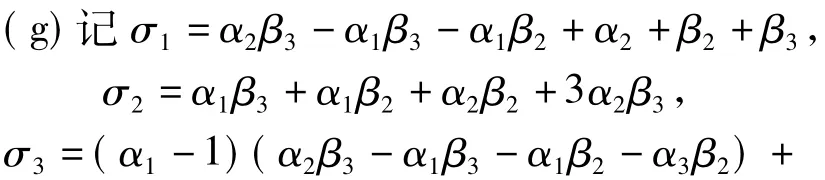
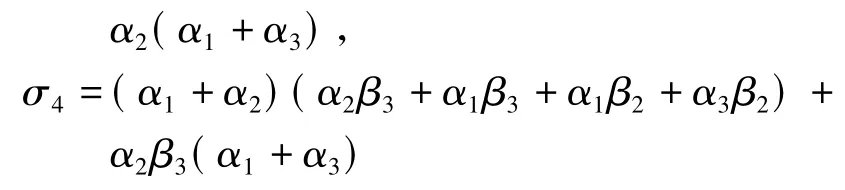
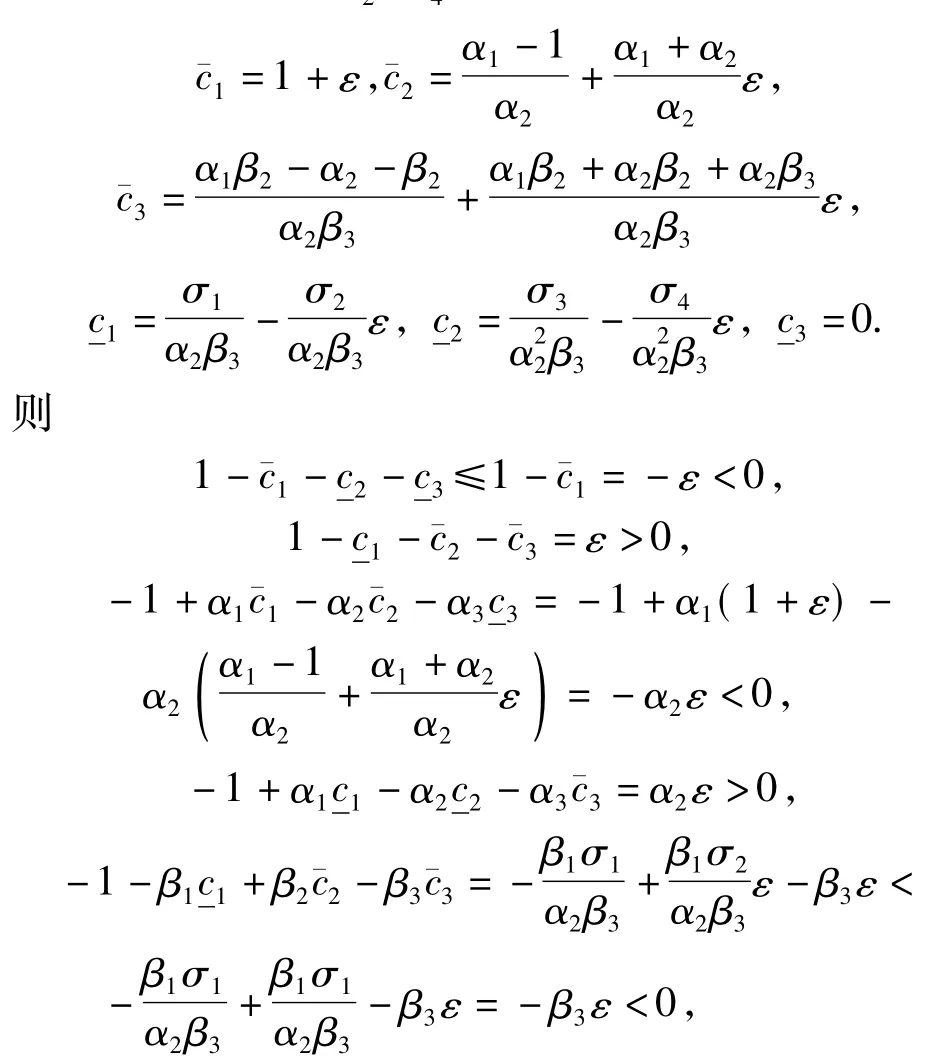
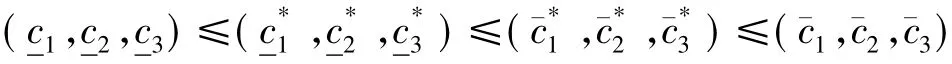
这表明式（6）满足.类似于情形（d）的证明步骤，知及式（7）～（12）成立.注意到，若，则式（7）～（12）可约化为

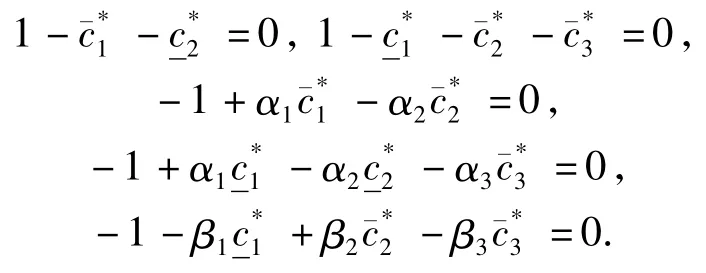
对上式求解，得

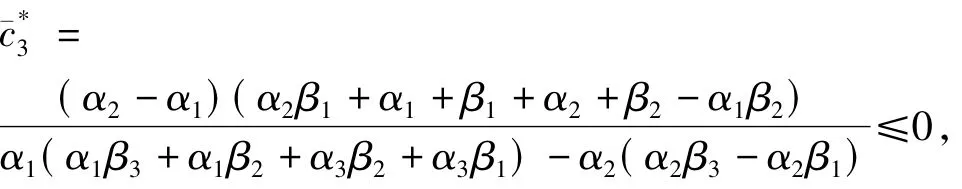
注1在定理2中，平凡解与非负半平凡解的全局渐近稳定性条件不依赖于各个种群的扩散率，因此，定理2的结论同样适用于某个di=0或所有di=0的抛物-常微分系统.

注2由定理2知，若本土物种u1的初始密度不恒为零，则有下述暗示:

（1）只有与u1构成竞争关系的单个外来物种u3入侵，则u3绝灭，u1持续生存；

（2）只有与u1构成捕食关系但捕食率足够小的单个外来物种u2入侵，则u2绝灭，u1持续生存；

（3）若u2与u3同时入侵u1，u3仅靠捕食u2存活，u2仅靠捕食u1存活且捕食率足够小，则u2与u3绝灭，u1持续生存；

（4）只有与u1构成捕食关系的单个外来物种u2入侵，捕食率无需足够小但小于u2的种内竞争率，则u2与u1均持续生存；

（5）若u2与u3同时入侵u1，u3的种内竞争率足够大但对u2的捕食率不大，u2对u1的捕食率小于u2的种内竞争率，则u3绝灭，u2与u1持续生存.

［1］王勤龙，李百炼.生物入侵模型研究进展［J］.科技导报，2011，29（10）:71-79. Wang Q L，Li B L.Progress in modeling biological invasion［J］.Science，Technology&Review，2011，29（10）:71-79.

［2］张林艳，叶万辉，江洪.利用反应-扩散模型预测生物入侵［J］.生态环境学报，2009，18（4）:1565-1572. Zhang L Y，Ye W H，Jiang H.The application of biological invasion prediction-illustrated reaction-diffusion model［J］.Ecology and Environmental Sciences，2009，18（4）:1565-1572.

［3］Kim K I，Lin Z G.Coexistence in the three species predator-prey model with diffusion［J］.Applied Mathematics and Computation，2003，145:701-716.

［4］林支桂.三种群捕食-被捕食模型中具时滞的抛物系统［J］.数学学报，2004，47:559-568. Lin Z G.Time delayed parabolic system in the three species predator-prey model［J］.Acta Mathematica Sinica，2004，47:559-568.

［5］Chen Y L，Wang M X.Asymptotic behavior of solutions of a three-species predator-prey model with diffusion and time delays［J］.Applied Mathematics Letters，2004，17: 1403-1408.

［6］Wang Y M.Asymptotic behavior of solutions for a class of predator-prey reaction-diffusion systems with time delays［J］.Journal of Mathematical Analysis and Applications，2007，328:137-150.

［7］Pao C V.Global asymptotic stability of Lotka-Volterra 3-species reaction-diffusion systems with time delays［J］. Journal ofMathematicalAnalysisandApplications，2003，281:186-204.

【中文责编：庄晓琼英文责编：肖菁】

Global Asymptotic Stability of a Weakly-Coupled Reaction Diffusion System in the Three-Species Model

Wu Chufen*
（Department of Mathematics，Foshan University，Foshan 528000，China）

Recently，with the increase of the invasive species，multi-group reaction diffusion model has been used in invasion ecology theory.The multi-group reaction diffusion model can combines the spatial and population process within the prediction of invasion rate，also the use of continuous parameters in the model made it free to broad spatial scale.This paper is concerned with the initial boundary value problem of a weakly-coupled prey-predator reaction diffusion model.By using the method of upper and lower solutions as well as iteration，sufficient condition are obtained for the global asymptotic stability of the trivial solution and the nonnegative semitrivial solutions with the homogeneous Neumann boundary condition.The results reveal by means of controlling the birth rate，interspecific，intraspecific interaction rate of populations to achieve the goal of certain population disappearance or certain population persistence.These conditions are easy to check and independent of the diffusion rates and thus the conclusions are also appropriate for the corresponding parabolic-ordinary differential system（di=0 for some or all i）.

three species；reaction diffusion system；nonnegative semitrivial solution；global asymptotic stability

O175.21；O175.26

A

1000-5463（2015）03-0142-06

2014-12-31《华南师范大学学报（自然科学版）》网址:http://journal.scnu.edu.cn/n

国家自然科学基金项目（11326123，11401096）；佛山科学技术学院优秀青年人才培育项目

吴楚芬，讲师，Email:chufenwu@126.com.