驱动滚珠的弧面分度凸轮运动轨道实体建模及仿真分析

杨春花

（云南机电职业技术学院机械工程系，昆明 650203）

驱动滚珠的弧面分度凸轮运动轨道实体建模及仿真分析

杨春花

（云南机电职业技术学院机械工程系，昆明 650203）

当前对弧面分度凸轮实体建模的研究方法有多种，研究的凸轮实体不仅变形比较严重，而且运动过程中振动也相对严重，导致转盘的角位移、角速度及角加速度实际值与理论值偏差较大，不能很好满足设计要求。对此，文章提出了驱动滚珠型弧面分度凸轮实体建模方法，采用Matlab软件对凸轮从动件的运动规律进行选择，然后编程运动规律曲线程序计算出运动轨迹的坐标点，导入到建模软件UG中，通过扫略切除凸轮毛坯基体，最后对弧面分度凸轮与转盘装配体进行运动仿真，并与其它建模方法及运动仿真进行了比较。通过比较可知，该方法不仅建模时间特别短，建模周期至少缩短了50%，而且运动仿真精度特别高，与以往建模方法相比，转盘运动仿真的角位移、角速度及角加速度实际值与理论值差别特别小，为弧面分度凸轮实体建模的研究提供了一种全新方法。

弧面分度；实体建模；仿真分析

0 引言

当前机械化设备种类层出不穷，有些机械化设备结构也相当复杂，这些机械化设备在生产加工过程中，根据产品加工的现实需要必须要周期性的停歇运动及分度运动。常见的间歇运动机构［1-2］主要有以下7种：①棘轮机构；②槽轮机构；③针轮机构；④不完全齿轮机构；⑤共轭盘形分度凸轮机构；⑥圆柱分度凸轮机构；⑦弧面分度凸轮机构。在以上几种间歇机构中，弧面分度凸轮机构因具有高精度、高性能、小体积、长寿命、低噪声等很多优点，被应用在加工中心、包装机械、印刷机械、装配自动生产线等各种机械。

目前对弧面分度凸轮实体建模的方法有很多种，大部分研究人员都是采用驱动滚子弧面分度凸轮实体建模与运动仿真，如图1所示。例如：文献［3］利用点—线—面法对弧面分度凸轮进行实体建模，把驱动滚子比作铣刀来切削凸轮毛配。文献［4］利用UG和VC++对弧面分度凸轮实行参数化建模与运动仿真。文献［5］对双凸轮联动自动换刀技术进行了研究。大部分研究的凸轮实体变形比较严重，导致转盘运动过程中振动相对严重，运动精度特别低。对此，本文提出了驱动滚珠型切除弧面分度凸轮毛坯基体方法，采用Matlab和UG两种软件，创建弧面分度凸轮实体模型，然后对弧面分度凸轮与转盘装配体进行运动仿真，最后将此方法与其它建模方法及运动仿真进行了比较，从而为弧面分度凸轮实体建模的研究提供了一种全新方法。

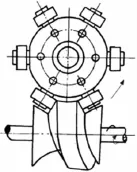
图1 弧面分度凸轮机构

1 弧面分度凸轮设计流程分析

为了能够对弧面分度凸轮精确建模，必须理解和掌握弧面分度凸轮的构造，从整体上把握和分析弧面分度凸轮的整个设计流程，如图2所示。

图2 弧面分度凸轮设计流程图

首先，要对弧面分度凸轮的运动过程进行分析，确定出弧面分度凸轮的分度期凸轮所旋转的角度，停歇期凸轮所旋转的角度。其次，比较凸轮从动件运动规律曲线在运动过程中有没有发生突变，尤其是比较凸轮从动件的角位移、角速度、角加速度及跳跃度四个参数，选择出最佳的凸轮从动件运动规律曲线，编写相应的凸轮曲线程序，输入到Matlab软件中计算出空间曲线的三维坐标点，把所得结果输入到UG三维软件中得到曲线，在曲线的垂直平面上画一个圆形，半径大小等于滚珠半径，通过扫略切除毛坯实体。最后，对弧面分度凸轮进行装配和仿真，仿真结果如果满足设计者的要求即可停止，否则重新设计，直到获得满意的结果为止。

2 转盘运动规律的选择

转盘运动规律在选择过程中，必须考虑转盘的角位移、角速度、角加速度及角跃度四个参数值的变化情况，从理论上要求后三个参数值的最大值在转盘运动过程中保持最小，即角速度最小、角加速度最小及角跃度最小，但是现实运动过程中很难找到这样的运动规律曲线。常见的转盘（凸轮从动件）运动规律曲线主要有以下六种［6-8］：①余弦加速度运动规律；②正弦加速度运动规律；③3-4-5次多项式运动规律；④改进等速度运动规律；⑤改进梯形加速度运动规律；⑥改进正弦加速度运动规律。通过综合比较六种运动规律曲线的最大值，得到改进正弦加速度运动规律曲线性能比较良好，最后选择改进正弦加速度运动规律作为转盘的运动规律。结合Matlab编写相应的程序，得到如图3所示。

图3 转盘与凸轮分度期运动规律曲线

从图3可以看出转盘的角位移、角速度角、加速度及跳跃度并没有发生突变，符合运动的要求。

3 弧面分度凸轮实体建模

3.1 弧面分度凸轮实体建模原理

弧面分度凸轮实体建模需要运动参数和几何参数，在这里就不详细阐述了，参数如表1所示。

表1 弧面分度凸轮设计的主要参数值

打开UG软件，在草图中画一个半径为92mm的圆和另一个半径为34mm的圆，通过拉伸命令拉伸86mm，然后在凸轮毛坯基体中间切除一个键槽，即可得到弧面分度凸轮毛坯基体，如图4所示，采用文献［5］所得到的弧面分度凸轮毛坯基体和本文一样。

图4 弧面分度凸轮毛坯基体

3.2 弧面分度凸轮空间坐标值计算

本文对凸轮从动件的运动规律进行了分析，最终选择改进正弦加速度运动规律作为弧面分度凸轮建模轮廓曲线，把无量纲时间 T、S、V和滚珠转盘建立联系。由弧面分度凸轮的工作曲面轮廓方程式［9-10］式可以编写计算空间坐标点程序，计算式子程序如下所示。

（1）滚珠1分度期程序

（2）滚珠2分度期程序

转盘滚珠2程序与转盘滚珠1程序相似，将φ1=0改成φ1=-pi/3就可以得到滚珠2分度期的整个程序。

（3）滚珠1停歇期程序

将滚珠1的分度期、停歇期程序及滚珠2的分度期程序，输入到Matlab软件中可以得到三维坐标点，然后将三维坐标点保存为文本形式导入到UG软件中，如图5所示。采用文献［5］方法所得结果如图6所示。

图5 本文凸轮运动理论轮廓曲线

图6 文献［5］凸轮运动理论轮廓曲线

3.3 弧面分度凸轮实体模型创建

选择图5中的一条曲线，在曲线的垂直方向上创建一个平面，在平面上画一个半径为20mm的圆，然后通过扫略切除即可得到凸轮实体模型，如图7所示。采用文献［5］所得弧面分度凸轮实体模型如图8所示。转盘的整个建模过程相对简单，此处不展开叙述。最后分别对两种建模的弧面分度凸轮与转盘进行装配，如图9，图10所示。

图7 本文凸轮实体模型

图8 文献［5］凸轮实体模型

图9 本文凸轮与转盘装配体

图10 文献［5］凸轮与转盘装配体

从图5和图6中可以看出，本文建模过程所需要的计算程序明显减少，只需要建立1条轮廓曲线，而文献［5］建模过程所需要的计算程序量明显增加，需要建立2条轮廓曲线程序，每条轮廓曲线所需要的计算程序也高于本文。通过对比可得，本文建模过程计算程序量至少减少了50%，建模速度特别快，从而提高了效率。

4 弧面分度凸轮装配及运动仿真分析

弧面分度凸轮设计的最后一步就是运动仿真，运动仿真结果可以直接反应出凸轮实体建模的好坏［5］。仿真结束后可以查看滚珠的角位移、角速度及角加速度随时间的变化状况，把仿真结果和理论值形成对比。如果差别较小，说明弧面分度凸轮实体建模精度较高，如果差别较大，就返回凸轮从动件运动规律重新选择，直到设计出优良的弧面分度凸轮为止。弧面分度凸轮装配完成后，就进行运动仿真，仿真结果的角位移、角速度及角加速度如图11、图12及图13所示。采用文献［5］仿真结果如图14、图15及图16所示。

图11 本文凸轮运动角位移曲线

图12 本文凸轮运动角速度曲线

图13 本文凸轮运动角加速度曲线

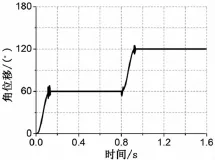
图14 文献［5］凸轮运动角位移曲线

图15 文献［5］凸轮运动角速度曲线

图16 文献［5］凸轮运动角加速度曲线

表3 弧面分度凸轮运动仿真参数值

通过图11、图12、图13和图14、图15、图16比较可知，采用驱动滚珠型建立的弧面分度凸轮实体仿真的角位移、角速度和角加速度在旋转5 结束语

运动过程中没有发生突变情况，振动比较小，运动相对平稳；而采用滚子型建立的弧面分度凸轮实体仿真的角位移、角速度和角加速度的在旋转运动过程中有发生突变情况，振动比较大，运动相对不平稳。运动仿真的角位移、角速度及角加速度与理论计算的最大值数据如表3所示。由表3数据可得，本文和文献［5］研究的角位移变化和理论值基本一致，没有太大的变化，本文研究的弧面分度凸轮驱动滚珠运动的角速度和角加速度与理论值几乎没有差别，而采用文献［5］研究的弧面分度凸轮驱动滚子运动的角速度和角加速度与理论值相差比较大。通过仿真结果可以证明，本文研究的弧面分度凸轮建模精度较高。

针对弧面分度凸轮建模过程的多样性与复杂性，本文采取驱动滚珠型切除弧面分度凸轮实体建模的方法，借助计算软件Matlab和三维建模软件UG完成弧面分度凸轮实体的创建。该方法不仅建模过程比较简单，建模周期至少缩短了50%，而且根本不需要了解编程语言。同时，转盘的运动仿真精度也特别高。此种建模方法为弧面分度凸轮深入的研究设计提供了参考价值。

［1］俞高红，陈志威，叶秉良，等.一种新型非匀速间歇机构的研究［J］.中国机械工程，2013，23（12）：2778-2782.

［2］尚继发.精密间歇运动机构智能测试系统［D］.大连：大连理工大学，2000.

［3］张文光，王大镇，弓清忠，等.单头弧面分度凸轮实体建模新方法及运动仿真［J］.组合机床与自动化加工技术，2014（2）：45-48.

［4］胡新蕾.基于UG的弧面分度凸轮机构的参数化设计及仿真分析［D］.青岛：青岛大学，2009.

［5］刘静.双凸轮联动自动换刀技术的研究［D］.大连：大连理工大学，2008.

［6］侯喜林，刘涛.弧面分度凸轮的三维实体建模与仿真加工［J］.现代制造工程，2012（9）：71-72.

［7］葛文杰，张王全.基于Pro/E的弧面分度凸轮机构参数化设计与仿真［J］.机械设计，2005（1）：12-14.

［8］周明贵，曹西京，曹巨江，等.弧面凸轮三维图形软件的开发［J］.工程图学学报，2005：151-154.

［9］刘建慧，邹慧君.加工中心自动换刀装置类型综述及设计特点［J］.机械设计与研究，2001，17（3）：49-52.

［10］丛明，刘静，李全普.复杂弧面分度凸轮精确建模的新方法［J］.中国机械工程，2009，10（6）：669-673.

（编辑 赵蓉）

Solid Modeling and Simulation Analysis of Globoidal Indexing Cam Trajectories of Driving Ball

YANG Chun-hua
（Department of Mechanical Engineering，Yunnan Vocational College of Mechanical&Electrical Technology，Kunming 650203，China）

Currently a variety of methods are proposed for researching solid modeling of globoidal indexing cams.The investigated solid cams not only suffer from serious deformation，but are also subject to relatively serious vibrations during motion，leading to a large deviation between the actual and theoretical values of the angular displacement，angular velocity，and angular acceleration of the turntable，making it fail to meet the design requirements.In this regard，this paper presents a solid modeling method for driving ball-type globoidal indexing cams and uses Matlab software for selection of cams in accordance with the motion law of the parts.Afterwards，the coordinates of the trajectories are calculated by programming the curve of movement rule，and then imported to the modeling software UG.By sweeping and removing the cam’s blank base，and lastly conducting motion simulation of globoidal indexing cam and turntable assembly，a comparison is made with other modeling methods and motion simulation.It can be found by comparison that this method not only features very short modeling time and 50%reduction of the modeling cycle，but also has particularly high motion simulation accuracy.Compared with the previous modeling methods，there is an extremely small deviation between the actual and theoretical values of the angular displacement，angular velocity，and angular acceleration of the turntable motion simulation，which displays a brand new method for the research of solid modeling of globoidal indexing cam trajectories of driving ball.

globoidal indexing；solid modeling；simulation analysis

TH132；TG659

A

1001-2265（2015）04-0083-04 DOI：10.13462/j.cnki.mmtamt.2015.04.021

2014-11-28；

2014-12-25

杨春花（1980—），云南建水县人，云南机电职业技术学院讲师，硕士，研究方向机械及其自动化，（E-mail）ych20141128@163.com。