多色集合与模糊遗传算法的机械产品概念设计研究*
杜 轩,吴 龙,张 屹
(三峡大学机械与动力学院,湖北宜昌 443002)
多色集合与模糊遗传算法的机械产品概念设计研究*
杜 轩,吴 龙,张 屹
(三峡大学机械与动力学院,湖北宜昌 443002)
针对机械产品概念设计中的优化问题,提出了基于多色集合与模糊遗传算法相结合的方案推理及优化方法。首先运用多色集合理论,建立了描述复杂结构机械产品各组成元素间的层次结构和复杂约束关系的信息模型,以进行有效的方案推理。然后,将多色集合推理模型与模糊遗传算法相结合,实现了方案的评价及优化方案的搜索。以工业机械手的概念设计为例对该方法进行了验证,结果表明,该方法能有效地实现概念设计过程中的方案推理及优化,为复杂机械产品概念设计提供了一定的理论基础。
机械产品;概念设计;多色集合;模糊遗传算法
0 引言
概念设计是产品设计中最重要的环节之一,也是提高产品质量、降低成本和提高企业竞争力的主要手段。概念设计的结果是产品设计方案,具体设计阶段很难甚至不能修改概念设计阶段的设计缺陷和错误[1-2]。机械产品的制造复杂、成本较高,因此机械产品概念设计在机械产品设计制造的过程中作用尤为重要。
对于机械产品的概念设计,许多学者进行了大量的研究。文献[3]将约束功能模型引入到机械产品的概念设计中,提出了基于机构映射的概念设计方法;文献[4]提出了基于功能方法树模型的包装机概念设计方法,文献[5]提出了基于多色集合的机械产品建模方法,建立了形式统一的数学推理模型;文献[6]在方案的优选中引入了模糊理论和遗传算法,为方案的优选提出了一种高效适用的方法。以上的文献从不同的角度对机械产品概念设计进行了研究,为机械产品概念设计的建模推理和方案评价等方面提供了较好的方法,但是这些研究都只针对机械产品概念设计的某一方面,机械产品的概念设计是需要将产品的建模和方案推理以及方案的优选结合,最后得出最优方案。
有鉴于此,本文提出了基于多色集合与模糊遗传算法相结合的机械产品概念设计方案推理及优化方法,在机械产品的建模中引入多色集合理论[5]建立产品的多色集合约束模型[5],同时运用该模型推理得出可行性方案集。在可行性方案的优选中,运用模糊理论[6]将评价指标量化,将多色集合约束模型与遗传算法的编码相结合,最后运用遗传算法完成机械产品方案的优选。为复杂机械产品的概念设计提供一种新的方法。
1 机械产品概念设计过程模型
一般认为,概念设计是指以设计要求为输入、以最佳方案为输出的系统所包含的工作流程。通常,概念设计输入功能要求输出结构方案,因此,它是一个由功能向结构的转换过程[7]。

图1 机械产品概念设计流程
图1描述了机械产品概念设计的工作流程,它主要由综合和评价两个基本过程组成。在综合部分,通过功能分析,将系统的总功能分解成相对独立的子功能单元,再找出可以实现该功能的所有方案元,最后将这些方案元进行组合,形成总的方案集。评价部分就是在得到的方案集中根据机械产品的功能指标,对方案进行定量评价,筛选出最优方案。其中,一般运用TRIZ理论[8]作为创新理论。
综合部分是由设计要求推理生成方案集,是一个发散的过程;评价则是从方案集中选择出最优方案,是一个收敛过程[7]。
2 基于多色集合的产品模型推理
2.1 多色集合理论简介
多色集合(Polychromatic Sets,简称PS)是俄罗斯的V.V Pavlov教授在2000年提出的[9]。PS的核心思想就是使用相同的数学模型仿真不同的对象,描绘元素间的层次结构和复杂关系在集合层和逻辑层组织和处理信息,在数量层解决底层数量大小问题[10]。
将集合A=(a1a2…ai…an)中的元素ai涂上颜色,形成的颜色集合F(ai)=(f1,…,fi,…,fn)称为元素ai的个人颜色。F(a)是所有个人颜色的集合。颜色集合F(S)=(F1,…,Fj,…,Fm)成为集合A的统一颜色,颜色Fj对应集合A的第j个性质。
在多色集合中,应用矩阵A×F(A)来描述个人颜色和统一颜色的关系,并且可以用布尔矩阵来表示[10]。

其中,若Fj∈F(ai),则aij=1,否则为0。

用矩阵[F(a)×F(S)]表示个人颜色与统一颜色的关系[10]。
式中如果个人颜色影响到统一颜色的存在,则cij=1,否则为0。
2.2 建立机械产品的多色集合模型
对机械产品进行功能到结构的逐层分解,并分析组成的部件之间存在的约束关系。产品在上一层的功能用多色集合的统一颜色表示,该功能分解的子功能或是实现该功能的结构用多色集合的个人颜色表示。
利用多色集合层次结构模型建立机械产品的多色集合模型的步骤为:
(1)对建模的对象进行分析,将需求功能进行逐层分解,如果分功能可以直接实现,或者有成熟的零部件相对应,则停止分解,否则,需要进一步划分下层的子功能。
(2)通过对组成部件之间的实现原理、尺寸、功能等进行分析,找出所有可能存在的约束关系[11]。
(3)详细定义各层的统一颜色Fi(A)和个人颜色Fi(a)。Fi(A)是第i层要实现的功能,Fi(a)是下一层需要实现的功能,即下一层的输入。
(4)建立推理矩阵和约束矩阵[(F(A),F(ai))×(F(A),F(ai))],用推理矩阵实现从上一层需求功能到下一层需实现功能的搜索过程,约束矩阵用于排除无效方案。
2.3 基于多色集合模型的方案推理
在多色集合中,一个推理矩阵就表示一层推理关系。在布尔矩阵(2)中,如果个人颜色fj影响到统一颜色Fj的存在,那么cij=1,否则cij=0。个人颜色和统一颜色之间的关系可以用析取(∨)和合取(∧)来表示[11]。即
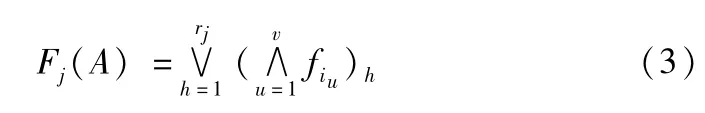

图2 基于多色集合的推理模型
图2为多色集合的推理模型,左上的布尔矩阵表示第一层推理关系,其中有●的元素表示为1的元素,否则元素为0。
3 基于模糊遗传算法的方案优选
引入模糊理论,将机械产品的评价指标量化,并将量化后的各个元件的评价值作为适应度函数。此处可以参照文献[6]中的方法。
利用遗传算法对可行性方案进行优选的步骤如下:
①染色体的编码
在多色集合的约束模型中,根据产品的功能需求,按照析取和合取的运算法则,推理出满足要求的元件,并对元件进行二进制多参数级联编码,产品每个部分的组成机构为一个基因片段,每个部分的染色体长度就是该部分满足要求的元件个数。每个部分只能选择一种机构,所以每段只能有一个基因值为1,其它基因值全部为0。
②评价指标的量化
利用模糊理论,将每个组成元件交由专家系统评分,根据公式将评价指标进行量化。
③确定适应度函数
根据组合优化取最大值。
④选择控制参数
由于可行性解集中已经去掉了无意义的接,种群的质量和遗传算法的效率有了很大的提高,所以在选择控制参数时,可以更偏重于考虑求解质量,故可以将算法执行的遗传代数M、交叉概率Pc和变异概率Pm都相对设置偏大。
4 工程实例
工业机械手概念设计的基本参数和要求如下:①工件性质为:质量较重、尺寸较大、形状为管状,非导磁材料;②方位调整要求是:绕z轴回转;③空间位置调整为:定位精度较高、灵活性较好。产品要求在经济性、机械性能、可维护性和通用性四个方面实现最优。
4.1 建立多色集合模型
首先要进行工业机械手的功能分解,并将功能要求和组成元件用多色集合中的元素代替如下:F11:工件质量轻,F12:工件质量较重,F13:工件质量重,F14:工件尺寸小,F15:工件尺寸较大,F16:工件尺寸大,F17:工件为圆柱形,F18:工件为方形,F19:工件为细小棒形,:工件为球形,F111:工件为管状,F112:工件为不规则图形,F113:上下调整,F114:左右调整,F115:旋转,F116:横向移动,F117:定位精度高,F118:定位精度较高,F119:定位精度低,F120:灵活性好,F121:灵活性较好,F122:灵活性差;F21:滑槽杠杆,F22:连杆杠杆,F23:弹簧杠杆,F24:斜楔杠杆,F25:齿轮齿条,F26:平面移动杠杆,F27:内卡传力,F28:V型指,F29:平面指,F210:细长指,F211:内卡指,F212:特型指,F213:回转液压缸,F214:齿轮齿条缸,:单作用活塞缸,F216:轴线垂直双回转液压缸,F217:齿轮齿条与单作用活塞组合,F218:两自由度链轮锥齿传动,F219:两自由度链轮锥齿传动,F220:链轮回转缸,:直角坐标式,F222:圆柱坐标式,F223:球式坐标,:关节式。其中表示第1层分解中的第i个功能元,表示第2层分解中的第j个元件。因为机械手的功能分解只有两层,第二层即分解到实现功能的方案元,所以在此机械手的多色集合模型中,只需要用布尔矩阵A×F(a)来表示层次推理关系。
因为机械手手部、手婉和手臂的功能相对独立,所以可以将其分为三个部分分别建立多色集合模型。
为了表达方便,以上的推理矩阵和约束矩阵都画在同一张图上,如图3所示,其中①~⑤分别为Md1、Md2、Md3、Md4和Mc。

图3 推理矩阵和约束矩阵
4.2 基于多色集合的方案推理
通过多色集合的推理矩阵和约束矩阵,可以得出满足要求的方案元为:传力机构:6个;手指:4个;手婉:7个;手臂1个。排除掉存在约束的手部方案,满足要求的可行性方案一共有91个。
将91个可行性方案作为遗传算法解的空间,由于在方案的推理中去掉了无效解,显著减小了解的空间,从而减小早熟的可能性和改善遗传算法的收敛速度。
4.3 基于遗传算法和模糊理论的方案优选
工业机械手的评价指标为Y1:经济性,Y2:机械性能,Y3:可维护性,Y4:通用性,采用评语集{很好,较好,一般,差}来表示各元件所得的专家评价,每个元件对4个评价指标的模糊评价矩阵为:

各个评价指标的权重向量为:

加权后的评价指标向量变为

22个元件对以上4个评价指标的综合评价如下表1所示:

表1 备元件综合评价
对评价集中的评语量化,则量化向量为

则机械手的方案优选模型为

其中yij为元件i对评价指标j的隶属度,适应度函数为

其中g为初始种群的规模,zi为第i个个体的适应度值。
设置初始种群大小为10,交叉概率Pc=0.6,变异概率Pm=0.2,最大进化代数为100,采用Matlab编程实现,得到最优目标函数值为28.68,相应的组合为,收敛曲线如图4所示,从遗传算法的收敛曲线可以看出,在方案优选的过程中,算法的收敛速度比较快,而且模糊遗传算法的稳定性比较好。
运用多色集合和模糊遗传算法的机械产品概念设计方法能够用形式统一的数学模型描述复杂结构机械产品各组成元素间的层次结构和复杂约束关系的信息模型,在方案优选的过程中能够更好地便于最优方案的遴选。该方法适合计算机的编程,便于实现机械概念设计的自动化和智能化。

图4 遗传算法收敛曲线
5 结束语
本文在机械产品的概念设计中建立了多色集合的约束模型,并通过多色集合模型推理得到不含约束的可行性方案,保证了解的有效性,而且通过显著缩小方案优选中遗传算法解的空间而减少早熟收敛的可能性和改善收敛速度。在方案的决策优选过程中引入模糊理论,将定性的评价指标量化,将模糊理论与遗传算法融合用于方案的优选,并详细讨论了其具体的算法,为机械产品以及其他产品的概念设计提供了一种新的方法。
[1]尹碧菊,李彦,熊艳,等.基于概念设计思维模式的计算机辅助创新设计流程[J].计算机集成制造系统,2013,19(2):263-273.
[2]闫喜强,李彦,李文强,等.一种支持多利益相关者协商的复杂产品概念设计方法[J].四川大学学报,2012,44(9):226-232.
[3]高瞩,吉跷民,高峰.基于约束功能的机械产品概念设计方法研究[J].机械设计与制造,2013(5):256-259.
[4]张广军,唐敦兵.基于改进型功能方法树的产品概念设计[J].机械设计与制造,2009(1):13-14.
[5]周宪.基于多色集合的大规模产品定制形式化解决方法[J].计算机应用研究,2013,30(11):3362-3364.
[6]孔凡国,黄伟.基于模糊理论和遗传算法融合的机械方案优选方法的研究[J].组合机床与自动化加工技术,2006(5):35-38.
[7]张建明,魏小鹏,张德珍.产品概念设计的研究现状及其发展方向[J].计算机集成制造系统,2003,9(8):613-620.
[8]张建辉,檀润华,张鹏,等.计算机辅助创新驱动的产品概念设计创新设想产生过程模型[J].计算机集成制造系统,2013,19(2):284-292.
[9]Pavlov V V.Polychromatic sets and graghs for CALS in machine building[M].Moscow:Stank in Press,2002.
[10]李宗斌,高新勤,赵丽萍.基于多色集合理论的信息建模与优化技术[M].北京:科学出版社,2010.
[11]高新勤,李宗斌,赵珊珊.基于多色集合理论的概念设计建模和推理技术研究[J].中国机械工程,2006,17(3):255-259.
(编辑 赵蓉)
Research Study on the Conceptual Design of Mechanical Products Based on the Combination of Polychromatic Sets and Fuzzy Genetic
DU Xuan,WU Long,ZHANG Yi
(College of Mechanical&Power Engineering of China Three Gorges University,Yichang Hubei443002,China)
Aiming at solving the optimization problems in the conceptual design of mechanical products,proposal reasoning and optimization approach are proposed based on the combination of polychromatic sets and fuzzy genetic algorithm.To describe the hierarchy and complicated constraints relationship among different components of complex structure mechanical products,the polychromatic sets theory is applied to carry out the proposal reasoning effectively.The proposal evaluation and the searching of optimization approaches are achieved based on the combination of polychromatic sets theory reasoning model and fuzzy genetic algorithm.An instance of industry manipulator is illustrated to verify the effectiveness of the proposed methods. The results show that the proposed methods can achieve the effective proposal reasoning and optimization during the process of conceptual design,which lays some foundation for conceptual design of complex mechanical products.
mechanical products;conceptual design;polychromatic sets;fuzzy genetic algorithm
TH122;TG506
A
1001-2265(2015)04-0015-04 DOI:10.13462/j.cnki.mmtamt.2015.04.004
20104-07-28;
2014-09-03
国家自然科学基金项目(51275274);湖北省自然科学基金项目(2014CFC1141)
杜轩(1972—),男,湖北宜昌人,三峡大学副教授,博士,研究方向为复杂制造系统建模、仿真、分析及优化,(E-mail)xdu@ctgu.edu.cn。

