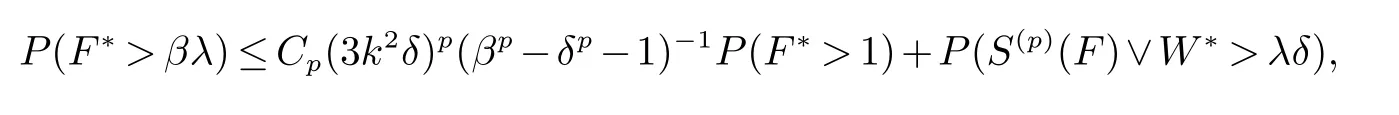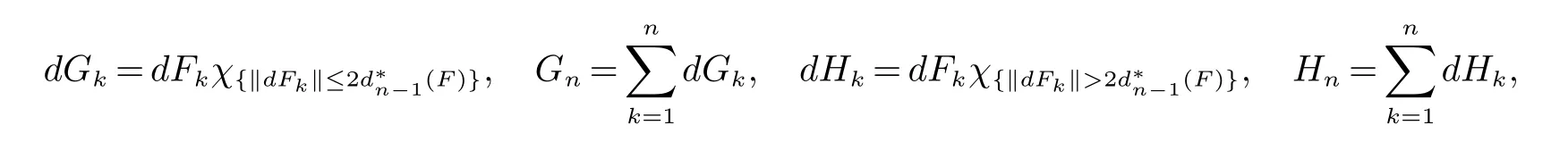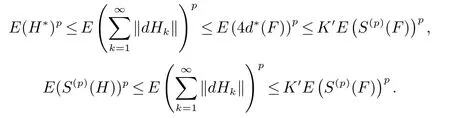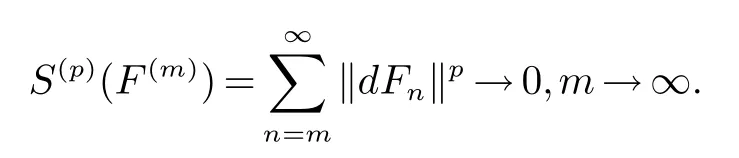关于三角鞅和Banach空间的TP光滑性的注记∗
陈亮,黄永峰,赵新科
(1.昌吉学院数学系,新疆昌吉831100;2.新疆大学学报编辑部,新疆乌鲁木齐830046)
众所周知,Banach空间值鞅理论有不同于实值鞅的独立价值且Banach空间值随机过程的概率性质与Banach空间的几何性质之间是相互依存、相互制约的.刘培德[2,3]首先对Banach空间值鞅引入了p均方算子p条件均方算子,并以此为工具研究了一系列基本的Banach空间值鞅不等式和鞅空间,揭示了Banach空间值鞅不等式和鞅空间的相互嵌入关系与在其中取值的Banach空间的一致凸性和一致光滑性之间的密切联系.贾正智,龚小兵[1]定义了TP一致光滑Banach空间和TP一致凸Banach空间,并利用三角鞅不等式对这两种几何性质进行了刻画.
1 定义及引理
文章利用三角鞅的收敛性、三角鞅的具体的Luxemburg范数不等式以及三角鞅的大数定律来刻画Banach空间的TP一致光滑性.若非另加说明,本文中X均指实Banach空间.
设X是Banach空间,是T中定义的X值p次可积函数的空间,满足:中的一个n次三角多项式是指记这种三角多项式生成的子空间.
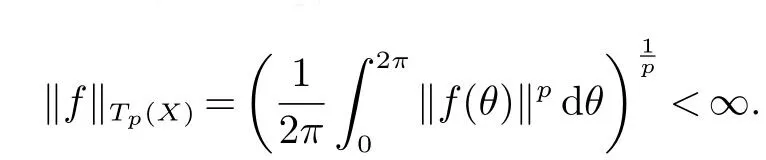
定义1设T=[0,2π],Ω=T N(N为正整数). 记θ ∈T N为θ=(θ1,θ2,···,θN),Ω 上定义的测度为乘积测度P,以BN记(θ1,θ2,···,θN)生成的σ代数,一个定义在 Ω 上的X值随机变量序列F:=(Fn)(n≥0)称为三角(多项式)鞅(简称为三角鞅或TP鞅),若F满足:
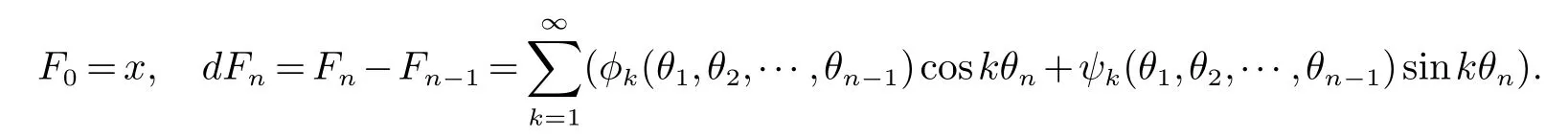
这里φk,ψk是仅与θ1,θ2,···,θn−1有关的关于Bn−1可测的X值函数.记A为X值三角鞅全体.
定义2设(Ω,Σ,µ)是概率空间,(Bn,n≥0)是Σ的递增子σ代数序列,与(Bn)适应的X值鞅记为F=(Fn,Bn,n≥0)或者F=(Fn).设dFn=Fn−Fn−1,F−1=0,B−1={∅,Ω}序列dF=(dFn)是鞅F=(Fn)的鞅差序列,对于F=(Fn),记
定义3对τ>0,(0<τ<1)定义X的TP 光滑模为
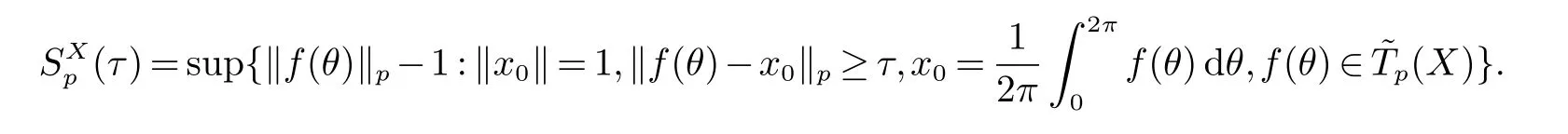
称X为一致TP光滑的,若称X是p一致 TP 光滑的,若使得
关于X的一致TP光滑性与一致光滑性有以下基本结论.
引理1[4]设X是Banach空间,则当X是p一致TP光滑空间时,X必是p一致光滑的.
引理2[4]若Banach空间X是p一致光滑的(1 引理3[4]Banach空间X是p一致可光滑的(1 利用三角鞅的收敛性、三角鞅的具体的Luxemburg范数不等式以及三角鞅的大数定律,给出Banach空间的 TP一致光滑性的四种等价刻画. 定理1设X是Banach空间,1 证明(=⇒)由Pisier不等式及Lp(µ,X)易证.事实上,给定n≥0,对于任意的其中则由于因此Fn依Lp(µ,X)范数收敛. (⇐=)由蕴含Fn依Lp(µ,X)范数收敛,知Fn依概率收敛.由定理2.6.2[5]可以证明X是p一致可光滑空间,从而由引理2知X是p一致TP可光滑空间. 定理2设X为Banach空间,1 (i)X是p一致TP可光滑空间. (ii)∀F∈A,若S(p)(F)∈L∞,则Fn a.e.收敛. (iii)∀F∈A,若E(d∗(F)p)<∞,则{S(p)(F)<∞}⊂{Fn收敛}a.e. 证明由定理1及定理5[6]234易证. 定理3(Banach空间的TP光滑性与三角鞅不等式) 设X为Banach空间,1 (i)X是p一致TP可光滑空间. (ii)若φ(t)=tp(t∈R),则存在Cφ>0,使得∀F∈A满足F∗ φ≤Cφ S(p)(F)φ,其中·为φ(t)=tp诱导的Luxemburg范数. 证明(i)=⇒(ii)由引理3 知,∀λ>0,存在Cp>0使得定义停时其中(Wn)是(dfn)的可料强函数序列.由定理3[6]230证明可得 进而由引理4[6]225知,存在K>0使得E(F∗)p≤KE(S(p)(F)∨W∗)p.对F作Davis分解F=G+H,这里G=(Gn),H=(Hn)满足 (ii)=⇒(i)设F=(Fn)是满足S(p)(F)<∞的X值三角鞅,对于∀m≥1,定义鞅则 定理4设X为Banach空间,1 (i)X是p一致TP可光滑空间. (ii)∀F=(Fn)∈A,若则 证明(ii)=⇒(iii)是显然的.(iii)=⇒(i)设∀F=(Fn)∈A,若依概率收敛于0,由定理2.6.3[5]可以证明X是p一致可光滑的.从而由引理2知X是p一致TP可光滑空间. (i)=⇒(ii)由X是p一致TP可光滑空间知,存在X上的等价范数记为|·|使得X在此范数下是p一致TP光滑的.由引理3知X在|·|下是p一致光滑的(从而p一致可光滑),再由定理3[6]200即可得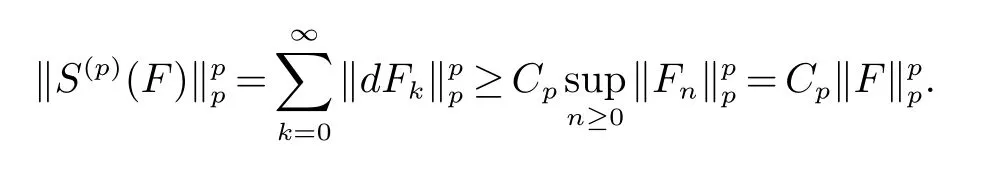
2 主要结论