指派问题匈牙利解法的注记∗

李智明

(新疆大学数学与系统科学学院，新疆乌鲁木齐830046)

0 引言

指派问题是一种特殊的整数规划问题[1,2]，指在满足特定分配要求的条件下，使分配方案总体效果最佳.如：N项任务分配给N个人完成，并且指定每人只能完成一项任务，每项任务只能交给一个人，应如何分配，使得费用最低[3,4].此类问题为最小化指派问题，匈牙利法是求解这类问题的常用方法之一，通过效率矩阵产生独立零元素，当独立零元素的个数等于矩阵阶数时，独立零元素对应的决策变量为1，其他元素对应的变量为0，得到了指派问题的最优解矩阵.下面给出一个实例.

例1[5]设A,B,C,D四个队员参加4×100米接力赛跑，由于各队员的心理素质、交接棒技术、起跑以及冲刺速度等原因，所跑不同棒次所用时间不尽相同(见表1).请给出各队员所跑棒次的最优排序.

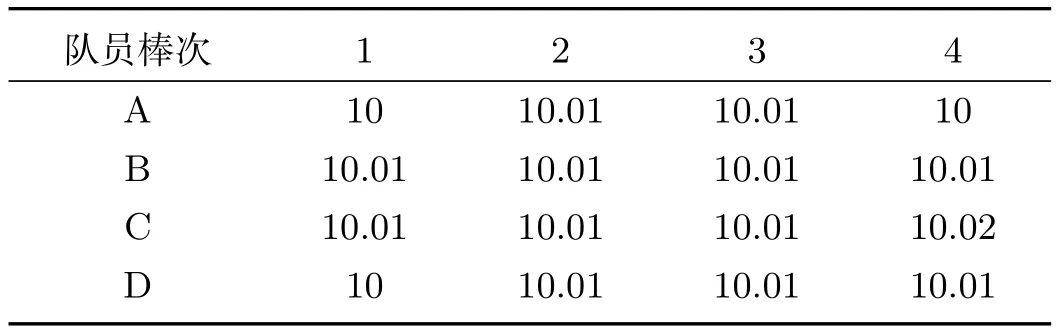
表1 队员接力赛所用时间（单位：s）

原解利用匈牙利法求解，求解过程为效率矩阵

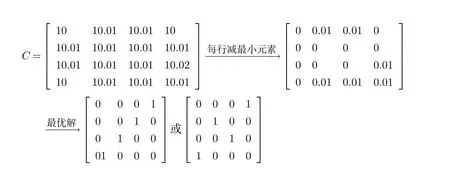
对于最大化问题，一般是先找出效率矩阵中的最大值，分别用这个值减去矩阵中的每一个元素，转化为最小化问题，再使用匈牙利法求解.观察例1中的效率矩阵，不难发现此效率矩阵每行有最小值，使得它们存在不同行不同列，称这些最小值为独立最小元素.对于这类效率矩阵，或者对于最大化指派问题的效率矩阵存在独立最大元素，即每行有最大值并且它们存在不同行不同列，能否不通过上述处理方法而直接得到最优解矩阵，这个问题在现有教材及文献中未见提起或者没有强调[6].

本文针对这两种情况，通过证明得到如下结论：将效率矩阵的独立最小元素或独立最大元素对应位置的决策变量取值为1，其他位置决策变量取值为0，得到最优解矩阵.尤其对于最大化指派问题的求解，不必再转化成最小化问题，这样就大大简化计算过程，更快找到最优解.

1 最小化问题效率矩阵存在独立最小元素

求解N个资源、N个活动的指派问题，使总效能最小.设cij>0表示分配资源i到活动j的效率，则决策变量

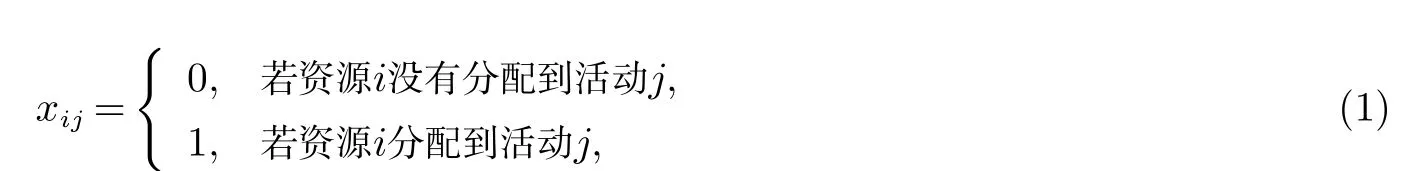
其中i,j=1,2,...,N.最小化指派问题的数学模型为

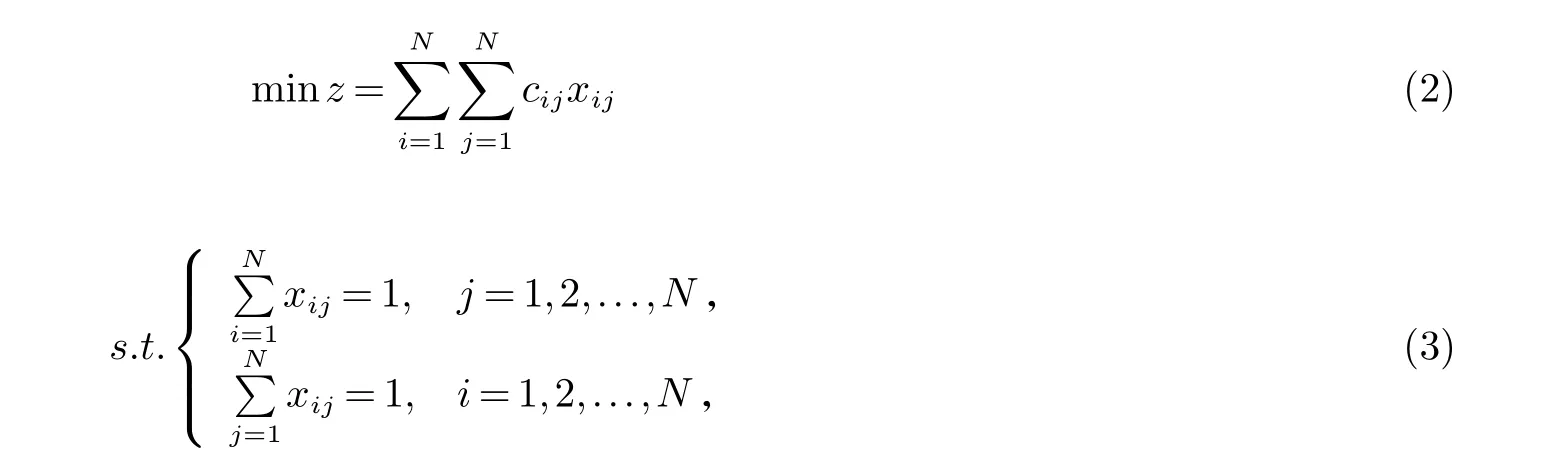
其中C=(cij)N×N为效率矩阵，其最优解矩阵用X=(xij)N×N表示.

定理1若式(2)中效率矩阵C=(cij)N×N存在独立最小元素，则这些元素对应的变量xij=1，其他元素对应的变量xij=0，矩阵X=(xij)N×N就是最小化指派问题的最优解矩阵.

证明因为效率矩阵C=(cij)N×N中每行的最小元素位于不同列，说明这些最小元素位于不同行不同列.根据匈牙利法，从矩阵C的每行元素减去该行的最小元素，就在对应的位置产生了不同行不同列的零元素.因此，在这些位置上令变量xij=1，其他元素对应的变量xij=0，就得到了最小化指派问题的最优解.

定理1说明当效率矩阵C=(cij)N×N中有独立最小元素时，不需要通过行或列变换产生独立零元素，只需要将这些最小元素对应的位置令xij=1，其他位置令xij=0，就得到了问题的最优解，省去了中间产生独立零元素的过程.由此可见，在产生独立零元素之前，先对效率矩阵进行观察其是否有“独立最小元素”，若有，通过定理1直接就可以得到问题的最优解矩阵.若没有，再由效率矩阵的行及列来产生独立零元素即可.下面对例1给出新解法.

例1新解由表1可知，每行对应的最小值分别为10,10.01,10.01,10，并且有两种方式使得这些最小值位于不同行不同列（用括号()表示）：

根据定理1，可得上述两个最优解.所以该队接力赛跑可以有两种最优指派方案：

（1）D→B→C→A；（2）D→C→B→A.所用总时间为10+10.01+10.01+10=40.02.

2 最大化问题效率矩阵存在独立最大元素

对于最大化指派问题模型的建立，只需要将(2)式中的目标函数改为

式(1),(3),(4)就组成了最大化指派问题的数学模型.

定理2若式(4)中效率矩阵C=(cij)N×N中存在独立最大元素，则这些元素对应的变量xij=1，其他元素对应的变量xij=0，矩阵X=(xij)N×N就是最大化指派问题的最优解矩阵.

证明若效率矩阵C=(cij)N×N中每行的最大元素位于不同列，不妨设为c1j1,c2j2,...,cNjN，其中j1,j2,...,jN∈{1,2,...,N}且它们均不相等.取

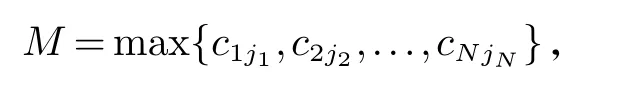
则M一定是效率矩阵C=(cij)N×N的最大值.用最大值M减去矩阵中的每一个元素，可知M−c1j1,M−c2j2,...,M−cNjN必为矩阵C每行中最小元素且这些元素位于不同列，由定理1可知，在这些最小元素对应的位置上，即最大元素的位置上令决策变量xij=1，其他元素对应的变量xij=0，就得到最大化指派问题的最优解矩阵.

对于最大化指派问题的求解，类似与最小化问题，首先观察效率矩阵是否有“独立最大元素”，若有，通过定理2直接就可以得到问题的最优解矩阵.若没有，可用匈牙利法的一般处理方法求解即可.

例2若一页文档被切割成4个条状碎片，序号分别为1,2,3,4，令

其中i,j=1,2,3,4.当i=j时，由于第i个碎片的一边无法与自身匹配，故xii=0,i=1,2,3,4.设cij(i,j=1,2,3,4)为第i个碎片的左边与第j个碎片右边的匹配度且cii=0，其匹配度矩阵为C=(cij)4×4如表2.

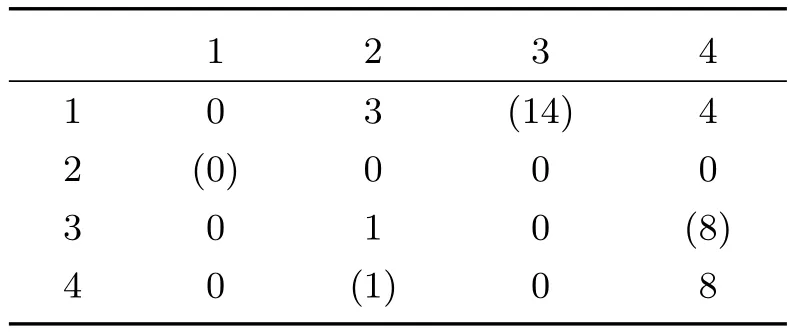
表2 碎片之间的匹配度

其中序号为1及2的碎片分别为碎片复原的左边界与右边界.易知，碎片匹配模型的目标函数为式(4)，约束条件为式(3)，匹配矩阵（或效率矩阵）C=(cij)4×4由表2决定，这个模型为最大化指派问题.

通过表2观察可知，匹配矩阵C中有独立最大元素(用括号()标记的元素)，根据定理2可知此模型的最优解矩阵为

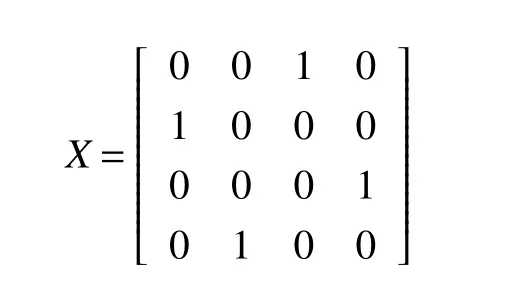
注意，通过表2已知最优解中x21并不表示序号2与1中匹配，只是为了凑成4个“独立的元素1”，故它的取值用括号()标注.从最优解矩阵中可以看出碎片的匹配顺序为：1,3,4,2，并且利用最优解可计算最大总匹配度为

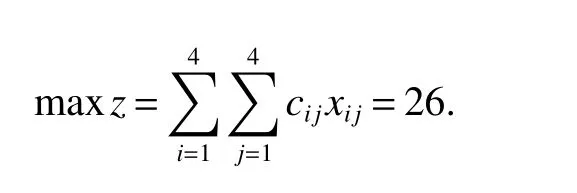
3 结论

对于最小化或最大化指派问题，首先要观察效率矩阵中是否存在独立的最小或最大元素.当效率矩阵具有这种特点时，仅需在最小或最大元素对应的位置取决策变量为1，其他位置取值为0，直接得到了指派问题的最优解矩阵.当然，若效率矩阵没有独立的最小或最大元素，指派问题仍然利用匈牙利法去寻找效率矩阵的独立零元素来求最优解矩阵.