M矩阵与非负矩阵Hadamard积最小特征值的界*

李艳艳，蒋建新

(文山学院 数学学院，云南文山663000)

1 预备知识

令 N={ 1 ，2，…，n }表示自然数集，Cn×n(Rn×n)表示 n×n 复 (实)矩阵集，

下面给出将要用到的一些基础知识.

设 A=(aij)∈Rn×n，若 aij≥0，则称 A 为非负矩阵(A≥0);若 aij≤0，i≠j，则称 A 为 Z 矩阵;进一步如果 A为Z矩阵，且A－1≥0，就称A为非奇异M矩阵，并用Mn表示非奇异M矩阵的集合;若A是不可约非负矩阵，则存在正向量u使A u=ρ(A)u，其中u称为A的右Perron特征向量;A是不可约非奇异M矩阵，则存在正向量v使A v=T(A)v，其中v称为A的右Perron特征向量.

矩阵 A=(aij)，B=(bij)∈Rn×n的 Hadamard 积为 A·B=(aijbij)∈Rn×n.

令q(A)=min{Re(λ):λ∈σ(A)}表示矩阵A的最小特征值，ρ(A)表示矩阵A的谱半径，σ(A)是Z矩阵A的特征值的集合.

若 A，B∈Mn，Fiedler M［1］证明了 A·B－1∈Mn.

2 主要结果

引理 1［2］设 A，B，C，D∈Rn×n，其中 C，D 是对角矩阵，则

一方面设矩阵 B－1·A 不可约，那么 A，B－1也不可约，令 D=diag(d1，d2，…，dn)，di＞0，因为 D－1B－1D 为非负不可约矩阵，则存在正向量 u=(u1，u2，…，un)，使得(D－1B－1D)u=ρ(D－1B－1D)u=ρ(B－1)u ，若写成分量形式，有

再设 U=diag(u1，u2，…，un)，令 C=(DU)－1B－1(DU)，则

G·B－1也为不可约非奇异 M 矩阵，又由引理 1 知，(FV)－1(A·B－1)(FV)=(FV)－1A(DU)·B－1=G·B－1，即q(A·B－1)=q(G·B－1)= λ，又由引理 2 知存在 i，使得

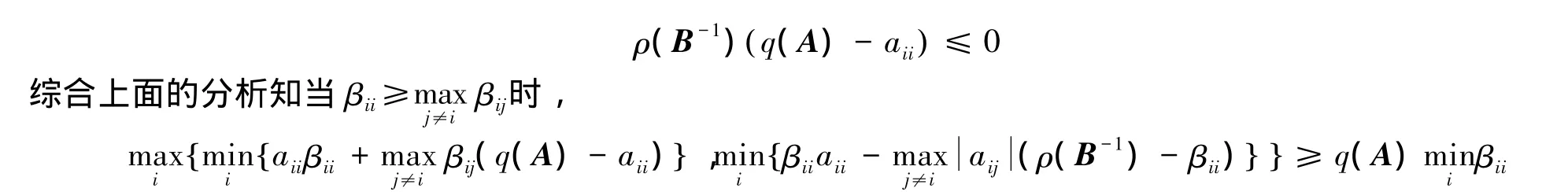
此处的估计式一定情况下提高了经典估计式q(A·B－1)≥q(A)miniβii.

3 数值算例

算例说明此处估计式提高了现有的结果.

［1］FIEDLER M，MARKHAM T.An Inequality for the Hadamard Product of an M-matrix and Inverse M-matrix［J］.Linear Algebra Appl，1988(101):1-8

［2］陈景良，陈向晖.特殊矩阵［M］.北京:清华大学出版社，2000

［3］黄荣.Some Inequalities for the Hadamard Product and the Fan Product of Matrices［J］.Linear Algebra and Its Applications，2008(428):1551-1559

［4］HORN R A，JOHNSON C R.Topics in Matrix Analysis［M］.New York:Cambridge University Press，1991

［5］CHEN SC.A Lower Bound for the Minimum Eigenvalue of the Hadamard Product of Matrix［J］.Linear Algebra Appl，2004(378):159-166