积分算子的线性性和有界性*
耿立刚,曾 静
(重庆工商大学数学与统计学院,重庆400067)
在泛函分析中,积分算子T又称积分变换是具有(Tf)(u)=(t,u)f(t)d t形式的变换.此变换把函数映为函数,是把函数空间映到函数空间上的变换.其中的K(t,u)是个确定的二元函数,称为此积分算子的核函数或核,f(t)称为象原函数,Tf(u)称为象函数.当选取不同的积分域或核函数时,就得到不同的积分变换.积分变换常用来处理微分方程的问题,常见的积分变换有Fourier变换、Laplace变换、Mellin变换、Abel变换及Hilbert变换等.此处将对积分算子的一些代数性质如线性性、有界性等进行研究.
1 积分算子的线性性
定理1 设算子T是从函数空间X到函数空间Y上的算子,如果对于任意的f,g∈X以及常数α都有式(1)(2)成立:

则称算子T是从X到Y的线性算子.
定理2 积分算子T:X→Y是线性算子.
证明 设f,g∈X,α是任一常数,则对于积分算子T,根据积分的性质有
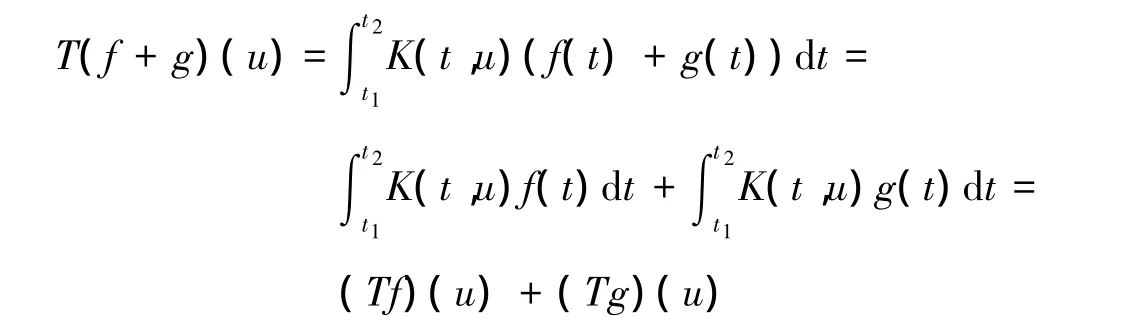
即T(f+g)=Tf+Tg.

即T(αf)=α(Tf),即证积分算子T是线性算子.
2 积分算子的有界性
算子T的范数指的是算子范数,定义为

对于算子T,如果 T<∞,则称算子T是有界算子.根据积分的性质,易知积分算子是否有界与核函数K(t,u)及积分域有关.
定理3 如果一个积分算子的积分域是有界集,并且核函数是有界函数,那么这个积分算子是有界算子.

由此可得 TfY≤M1fX,则 T≤M1<∞,即积分算子T是有界线性算子.
定理4 如果一个积分算子T的积分域是有界集,并且核函数是有界函数,那么这个积分算子T是连续的.
证明 因线性算子的有界性和连续性是等价的,由定理3,积分算子在所假设条件下是有界的,故积分算子T在定理假设条件下是连续的.
3 单位圆盘上的积分型算子

根据积分的性质,易知Jg的有界性.
定理5 积分算子Jg是有界的线性算子当且仅当g(z)是上的有界函数.
证明 充分性:由Jg的定义,积分域是有界的,根据定理3可得积分算子Jg是有界算子.
必要性:由算子范数定义

积分算子在泛函分析领域的研究中具有广泛的应用,并且在一些具体的理论研究中起着关键性的作用.根据Schwarz核定理,如果核函数是个广义的函数,所有的线性算子都是积分算子.Frodholm理论就是对一般积分方程理论的研究,在Frodholm理论中,核一般是Banach函数空间上的紧算子.在此情形下,核有时也称为Frodholm算子、核算子及Frodholm核等.
[1]欧阳光中,朱学炎,金福临,等.数学分析[M].3版.北京:高等教育出版社,2007
[2]POLYANIN A D,MANZHIROV A V.Handbook of Integral Equations[M].CRCPress,Boca Raton,1998
[3]MANZHIROV R K,THAMBYNAYAGAM.The Diffusion Handbook:Applied Solutions for Engineers[M].McGraw-Hill,New York,2011

