借助典型试题，加强回顾反思

☉安徽省马鞍山市二中实验学校　汪宗兴

☉安徽省马鞍山市薛镇初级中学　李道华

借助典型试题，加强回顾反思

☉安徽省马鞍山市二中实验学校汪宗兴

☉安徽省马鞍山市薛镇初级中学李道华

中考数学复习离不开解题，提高解题教学效果、提升复习效率是一项很有价值的议题.波利亚在《怎样解题》一书中，把解题的思维过程分解为四个步骤，包括：“弄清问题”→“拟定计划”→“实现计划”→“回顾与反思”.其中回顾与反思是最易被忽略的环节.解题教学中，及时引导学生进行解题反思，提炼规律，优化解题过程，有益于养成精益求精的学习习惯，发展思维能力，有效提高解题技能.下面笔者以在马鞍山市初中数学教师QQ群中讨论的一道典型题为例，谈谈实践的体会.

一、原题呈现

如图1，在正方形ABCD中，取AD、CD边的中点E、F，连接CE、BF交于点G，连接AG，试判断AG与AB是否相等，并说明道理.

图1

图2

该题以我们熟知的正方形为背景，条件简洁，问题明确，解法多样，是活化学生思维的极好素材，选作中考复习题用，是一道上佳的题目.

二、思路呈现

思路1：利用直角三角形斜边上的中线等于斜边的一半证明.

证明1：如图2，延长BA、CE交于点H.

由E是正方形ABCD的边AD的中点，得AE=DE.又∠EAH=∠D=90°，∠AEH=∠DEC，则△AEH≌△DEC（ASA）.

则AH=DC=AB.

思路1是学生1提供的，他首先考虑全等法，很快被否定；又利用等角对等边证明，但证角相等没有成功；再根据条件得CE⊥BF，得直角三角形HGB，利用直角三角形斜边上的中线的性质得证.根据解题经验，证明线段相等的方法还有很多，学生2巧用垂直平分线的性质证，见思路2；证明△ABG是等腰三角形，考虑到大多数学生未学“四点共圆”知识，笔者本着为优等生进一步发展服务，给予了点拨提示，见思路3.

图3

图4

图5

思路2：利用垂直平分线的性质定理证明.

证明2：如图3，作BC的中点H，连接HA，交BF于M.

则AE∥CH，AE=CH.

则四边形AECH是平行四边形.

则CE∥AH.

由证明1得BF⊥CE，则AH⊥BF.又BH=HC，则BM= MG，即AM是BG的垂直平分线.

则AG=AB.

思路3：构造辅助圆，利用等角对等边证明.

证明3：由∠BAD+∠BGE=180°，得A、B、G、E四点共圆，如图4所示，连接BE，则BE是该圆的直径.

则∠AGB=∠AEB.

由E是正方形ABCD的边AD的中点，正方形是轴对称图形，根据轴对称性可得∠DEC=∠AEB.

由证明1可得：∠CFB=∠DEC.

则∠AGB=∠CFB.又∠CFB=∠ABG，则∠AGB=∠ABG.

则AG=AB.

学生3利用勾股定理，将“几何证明”转化为“几何计算”，通俗易懂，见思路4.

思路4：利用勾股定理，求AG的长度，利用计算法证明（限于篇幅，过程从简）.

证明4：如图5所示，作GH⊥AD于H，不妨设AB=2a，则由勾股定理，得

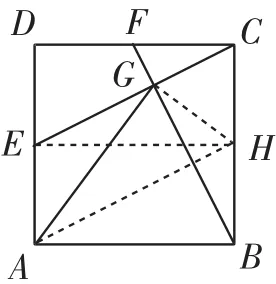
图6

图7

图8

学生4受图3的启发，构造如图6所示的图形，直接证AG=EH，于是想到证明四边形AEGH是等腰梯形，见思路5；许多同学开始另辟蹊径，“创造”新的证法，利用相似证明，见思路6.

思路5：利用等腰梯形的对角线相等证明.

证明5：如图6所示，取BC的中点H，连接HA、HE、HG.

易知EH=AB.由证明2得四边形AECH是平行四边形，观察图6，AG、EH都是梯形AEGH的对角线，只要证明梯形AEGH是等腰梯形即可，即证GH=AE.

由证明1得BF⊥CE.

思路6：利用三角形相似证明.

分析：由证明3得A、E、G、B四点共圆，则∠BAG=∠BEC.易知△ABG∽△EBC，反过来，能否通过证明△ABG∽△EBC，△EBC是等腰三角形，得到AG=AB呢？

证明6：如图7所示，连接BE.

由正方形ABCD的轴对称性，得∠ABE=∠CBF，EB= EC.

由∠ABE=∠CBF，得Rt△ABE∽Rt△GBC.

又∠ABE+∠EBG=∠CBF+∠EBG，即∠ABG=∠EBC，则△ABG∽△EBC.

事实上，采用证明6的方法，如图8，利用△ABG∽△FBA亦可证明结论，这两个三角形有一个公共角，只要证，而AB=CB，即证，利用基本图形“双垂图”易得.

图9

图10

图11

笔者将此题放入马鞍山市初中数学教师QQ群，很快群内有老师也利用相似证出，见思路7；本题可否用三角形全等直接证明呢？笔者也作了尝试，获得了成功，如图10，见思路8.

思路7：利用四点共圆、三角形相似证明.

分析：证明△BFE∽△ADG，利用△BFE是等腰三角形证AG=AD.

证明7：如图9所示，连接BE、EF、DG.

由证明1得BF⊥CE，则∠EDF+∠EGF=180°，即D、E、G、F四点共圆.

则∠FEG=∠FDG，∠EFG=∠EDG.

则△CFE∽△CGD.

由正方形及其对称性，得AD=CD，CE=BE=BF.

又∠EFG=∠EDG，则△BFE∽△ADG.

则△ADG是等腰三角形，即AG=AD=AB.

思路8：利用三角形全等证明结论.

分析：以AG、AB为边构造全等三角形.

证明8：如图10所示，构造矩形GBHK，且使H、A、K共线，E是GK、AD的交点.

由∠H=∠CGB，AB=CB，∠ABH=∠CBG，得△ABH≌△CBG（ASA）.

则AH=CG，HB=GB，即矩形GBHK是正方形，下面只要证A是KH的中点即可.

事实上，如图11，作DK⊥CE于K，作AH⊥CE于H，连接DH、DG，易证△CBG≌△DCK，△EHA≌△FGC≌△EKD（AAS），得AH=DK=CG，则△HAD≌△GCD，得△HDG是等腰直角三角形，则∠DHG=∠DGH=45°，所以△DHK也是等腰直角三角形，即HK=DK，所以HG=HK+ KG=DK+KG=CG+KG=KC=GB，从而△AHG≌△CGB，故AG=CB.这种构造三角形全等的方法，要严谨地表述过程，还是比较烦琐的.过程虽“漫长”，但可以欣赏到“美丽的风景”，如证明过程中可知△HDG是等腰直角三角形，即∠DGE=45°，这说明DG平分∠EGF.

几何问题代数化，利用代数方法解决几何问题，数形结合，是解数学题的常用“法宝”，本题中的正方形为平面直角坐标系的建立创造了有利条件，解析法新颖独特，大大开阔了学生的视野，见思路9.

思路9：利用解析法将证明线段相等转化为求两点之间的距离问题.

分析：建立平面直角坐标系，利用解析法，将几何证明问题转化为函数计算问题，求出G的坐标，而G是直线BF、CE相交产生的.

证明9：如图12所示，分别以AB、AD所在直线为x轴、y轴，建立平面直角坐标系，不妨设AB=2，则A（0，0）、B（2，0）、C（2，2）、D（0，2）、E（0，1）、F（1，2）.

图12

三、反思呈现

1.教师方面

在解题教学中，题目是载体，解题是过程，方法和规律的揭示、策略和思想的形成是目的，因此，解题教学切忌就题论题，片面追求容量，忽视教学功能的发掘、开发.初三数学总复习时，学生已经有了较多的知识储备，教学中应不失时机启示学生融会贯通，综合运用所学知识、方法，从新的视角开辟解题通道，引导学生进行解题后的回顾与反思，是一项很有意义的思维活动.教学实践中，我们发现很多教师把解题教学片面地理解为习题讲解，在教学实践中缺少了解题思路的引导发现，缺乏对学生数学素养的培养.

2.学生方面

（1）解题层面的回顾反思.

反思计算是否准确，推理是否合理，思维是否周密，解法是否还有更多和更简单的等.

（2）学会解题层面的回顾与反思.

解题中用到了哪些知识？解题中用到了哪些方法？这些知识和方法是怎样联系起来的？自己是怎么想到它们的？困难在哪里？关键是什么？遇到什么障碍？后来是怎么解决的？是否还有别的解决方法、更一般的方法或更特殊的方法、沟通其他学科的方法、更简单的方法？同样的方法能用来处理更一般性的命题吗？命题能够推广吗？条件能减弱吗？结论能加强吗？这些方法体现了什么样的数学思想？调动这些知识和方法体现了什么样的解题策略？

3.对该典型试题的反思

从解题层面看，证明1～证明9说明本题证明方法多样，对学生的思维要求也不尽相同，有的仅利用熟知的初等知识，有的需要利用学生陌生的知识解决.

从学会解题层面看，证明1～证明9应用的数学知识有三角形全等、等腰三角形、相似三角形、垂直平分线、勾股定理、直角三角形斜边上的中线的性质、平行线等分线段定理、两点之间的距离、一次函数、求直线交点的坐标、图形变换、四点共圆等.本题的实质是证明线段相等，采取的方法有全等法、等角对等边、等腰梯形的对角线相等、三角形相似、计算法、解析法等；证明9建立平面直角坐标系，不添加其他辅助线，利用代数方法求解，通俗易懂，渗透了数形结合思想；涉及的基本图形有相似形中典型的“双垂图”等.初中数学许多核心知识、数学方法等，该题均有涉及，足见它强大的教学载体功能，对培养学生数学思维的灵活性很有好处.如何想到上述诸多思路？如图13所示，构造网格正方形，或许能给你一些启发！过A、D、C作BF的平行线，再过B、A、D作CE的平行线，根据平行线等分线段定理易证图中每个网格都是正方形，观察图形，AG和正方形ABCD的边长均为1×2型网格矩形的对角线长，上面的证明方法显然都是与图13相通的，受图13的启发，也可以AG、AD为斜边构造全等直角三角形证明.有的证明方法可能困难重重，如利用图11，证明△AHG≌△CGB，观察图13，就知道这种思路能够成功.对学生来说，想到一种思路时，他可能并不知道这种方法的烦琐程度，教师唯有鼓励他们坚持“走下去”，直至成功解决.待回顾反思、想出其他方法时，再进行方法的优化.图12坚持几何问题代数方法解的思路，加强了代数、几何知识间的联系，证明1～证明8将几何中各类核心知识融于一题，增强了知识间的联系，这样的做法，对改变学生固有的思维定势、拓展思维方式很有益处！

图13

四、结束语

波利亚指出，即便是相当优秀的学生，在得到了题目的解答，并将整个论证简洁地写下来以后，也会合上书，去找别的事做.一个好的教师必须理解这些，并使他的学生深刻地认识到：没有任何一个题目是彻底完成了的，总还会有些事情可以做.通过解题后的回顾与反思来改编、引申和推广问题，有利于发现数学问题与问题之间、方法与方法之间、概念与概念之间、体系与体系之间的包含关系、相似关系、相联关系等，并进一步发现数学内部之间各种各样的有机网络结构.解题之后进行推广引申，不仅可以培养学生的创新能力，还能帮助学生洞察本质，提高认识，居高临下，跳出题海！

1.［美］G.波利亚.怎样解题［M］.上海：上海科技教育出版社，2007.

2.徐彦辉.数学解题后的“回顾与反思”与数学问题的提出［J］.数学教育学报，2015（1）.

3.印冬建.一题多解的教学指向：激趣，理知，得法［J］.中学数学（下），2013（6）.

4.唐绍友.初三数学教学中渗透初、高中衔接的实践与思考［J］.中学数学（下），2015（3）.

5.钱云祥，蔡蓉.让解题思路来得更自然些——基于有效解题的教学策略研究［J］.中学数学（下），2014（11）.Z