球体切面投影评定深孔轴线直线度误差研究*

李少敏，于大国，王继明，郝永鹏

（1.中北大学　机械与动力工程学院，太原 030051；2.山西省深孔加工工程技术研究中心，太原030051）

球体切面投影评定深孔轴线直线度误差研究*

李少敏1，2，于大国1，2，王继明1，2，郝永鹏1，2

（1.中北大学机械与动力工程学院，太原 030051；2.山西省深孔加工工程技术研究中心，太原030051）

提出球体切面投影评定深孔轴线直线度误差方案，将球体切面作为搜索路径，建立了以最小包容区域原理为基础，以网格逐次逼近为寻优手段的评定深孔轴线直线度误差的数学模型；利用点集投影将空间直线度评定问题转化为平面内最小外接圆的求解，以球体切面垂线为基础对点集进行坐标变换搜索最优解，通过球体表面网格化逐次缩小寻优范围；球体切面投影评定方案可以为任意方向直线度误差的评定提供参考。

深孔；轴线直线度；网格逐次逼近；投影；球切面

0 引言

在机械行业形状误差评定是产品质量管控的重要环节，误差值的大小直接影响了产品的性能及使用寿命。制造行业将孔长径比大于5的孔称为深孔［1-2］。深孔零件形状误差的主要评定对象包括圆柱度误差、圆度误差、孔轴线直线度误差等。轴线直线度误差是深孔零件的重要检测对象，对零件正常工作有较大影响［3］。国家标准（GB/T11336—2004）介绍的直线度误差评定方法有两端点连线法、最小二乘法以及最小包容区域法。在三种评定方案中两端点连线法计算较为简便，但评定结果的原理性误差较大，最小二乘准则以残差平方和最小为标准评定直线度误差，但是最小二乘法并与形状误差评定的最小条件原则不完全一致，故该方法与实际误差值存在偏差。最小包容区域法以最小条件原则为指导，从待测工件形状切入进行直线度误差的评定，最小包容区域法是直线度误差检测的理想方案，但是由于方法实现困难，实际工程环节的运用较少。针对此状态，科研工作者提出了直线度误差评定的遗传算法，粒子群算法及量子算法［4-6］。

文章在最小包容区域法的基础上提出一种深孔轴线直线度误差评定的投影判别方案，以部分球面区域作为寻优路径，搜索深孔轴线直线度误差的最优解，将研究对象从空间问题转化到平面内求解，以提高误差计算精度。

1 球切面投影寻优评定模型

直线度误差按照空间位置分类有给定平面、给定方向和任意方向三种形式。深孔轴线直线度误差的评定为任意方向的直线度误差评定，按照最小条件原则其实质是依据深孔轴线的空间坐标求解其相对于评定基线的位置变动。最小包容区域法的核心是求解最大偏差的最小值，重点是符合条件的评定基线方程的求解。最小包容区域法的评定过程如下；

（1）检测深孔零件孔轴线上的离散点空间坐标信息，得到空间点集A如下；

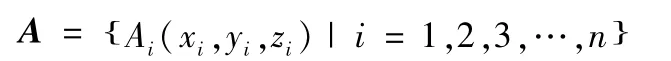
（2）依据得到的空间点集A，确定空间评定基线集合B如下；

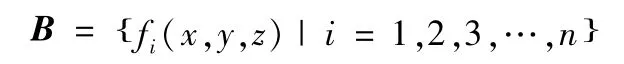
（3）依据得到的空间点集A及评定基线集合B，求解点集A中元素到评定基线fi（x，y，z）的最大距离ei，得距离集合ri，那么直线度误差值δ为；

对最小包容区域法可作如下描述；

最小包容区域法求解评定基线过程复杂，由于深孔轴线直线度误差在微米级别波动，可在某区域对评定基线进行寻优操作。寻优操作在圆心角为θ的圆球面上进行，球切面投影寻优评定评定模型如图1所示，将该方法称为投影面最小外接圆法，最小外接圆即为包含所有采样点且直径最小的圆。

图1 球切面投影寻优评定模型

投影面最小外接圆法优于基于最小包容区域法的最小外接包容圆柱。以直线fi（x，y，z）作为评定基线，方向向量为；

M为直线fi上一点，那么

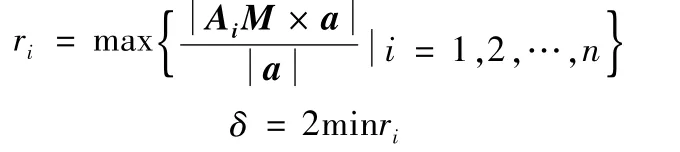
过直线fi上一点作垂面，沿直线fi方向向垂面Ⅰi投影所有点，在投影面Ⅰi内对所有点集计算其最小外接圆直径r′i；

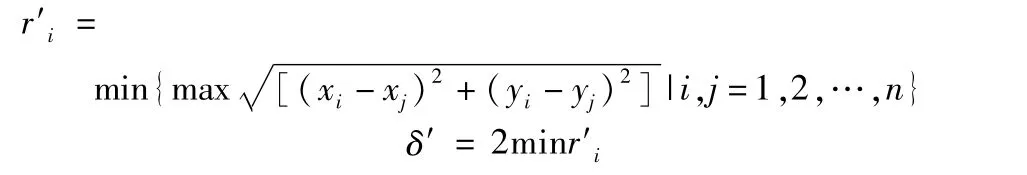
由上述分析知空间直线度评定的最小包容区域法基于一条直线及直线外点到直线的距离确定直线度误差δ，投影面最小外接圆法基于点集A中两点的距离求解最小外接圆直径δ′。而只有当投影面最小外接圆圆心处于评定基线上时有；

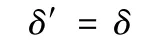
由于最小外接圆柱的评定原理，其求解原理是先确定评定基线再确定误差项，故在同一空间状态下（即同一坐标系下，评定基线，投影面已确定）有关系式（如图3所示）；

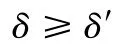
分析上述推理可知，同一空间状态下，投影面最小外接圆搜索最优解的速度要优于最小外接圆柱。直线度误差评定的最小包容区域法没有提出可行的寻优方案，球面寻优给出了合理的搜素范围，以球切面作为寻优搜索范围，球面切面垂线包含了连续的方向向量，投影面的方向在空间上具有连续性，便于寻优操作。

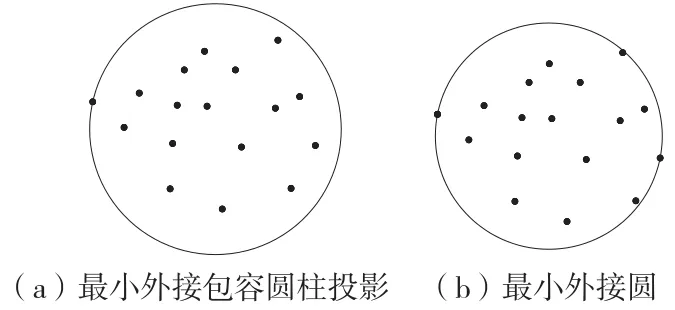
图3 球切面投影寻优评定模型

2 球切面投影寻优评定算法

球切面投影评定深孔轴线直线度主要研究以下方面的内容；

（1）网格逐次逼近方案

求解点集A相对于投影面的不同空间姿态，该操作有两种实现方案。其一，点集A保证静止，以球面为轨迹调整坐标系空间姿态；其二，坐标系保证静止，以球面为轨迹调整点集A空间姿态。为便于求解采用第一种方案，坐标变换点集A后得到点集Ak；

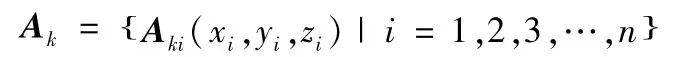
点集A空间姿态的调整有三种变换形式，分别为绕不同轴的旋转，正方向的确定；以右手定则为依据确定旋转方向，使大拇指指向与旋转轴正方向同向，则旋转的正方向为其余手指的指向，从旋转轴方向看，旋转的正方向为逆时针。绕x轴旋转α角的变换矩阵为Rx（α），绕y轴旋转β角的变换矩阵为Ry（β），绕z轴旋转γ角的变换矩阵为Rz（γ），变换矩阵如下；

搜索范围由首尾两点的距离L与角度θ进行确定。如图4所示，球体半径为R；

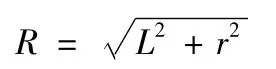
搜索球面所对应的角度θ为；

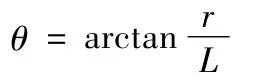
孔一侧的端点坐标为A1（x1，y1，z1），那么球面搜索区域ψ为；

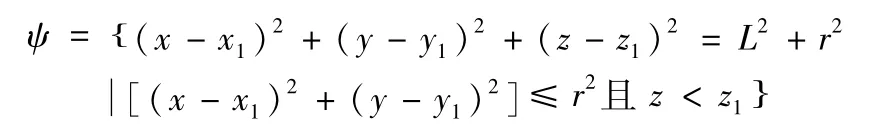
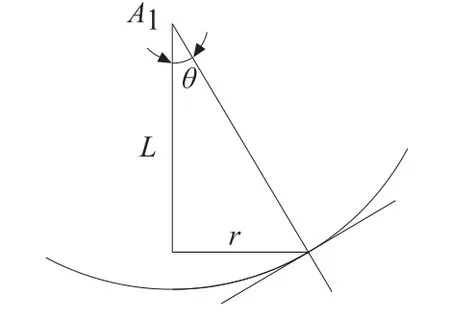
图4 搜索范围的确定

采用网格逐次逼近法确定最优解搜索路径。将确定的搜索球面平均划分为网格，网格端点集合记作D；

连接点集A首末两点有向量；

该向量绕z轴旋转γ角，绕y轴旋转β角，变换后的向量与z轴平行，由变换矩阵求得向量与角度间数值关系如下；

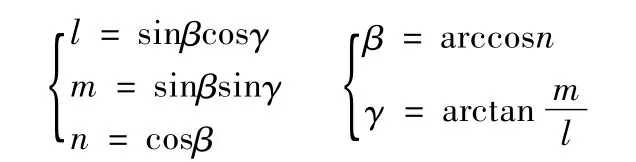
网格逐次逼近算法描述如下；

按照以上旋转方式对点集A预处理得A′，以A′为基础进行网格逐次逼近，记网格集合为W；

向量DiA1为网格端点与球心连线，该向量与过Di（xi，yi，zi）的球体切面垂直。每个点Di（xi，yi，zi）对应一个向量DiA1，以每个向量为基础，进行一次点集A的坐标变换，根据DiA1对点集A′进行变换，使AnA1其与DiA1平行。进而得到点集A′不同的空间姿态A′k及相应条件下对平面xy投影点的最小外接圆直径。

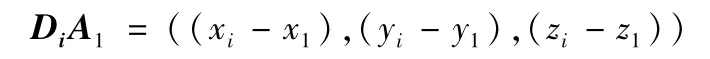
当满足以下条件时选取Wp作为下一次网格细分对象，对该网格区域进行细分（如图5及图6所示）即；

图5 网格化思想示意图

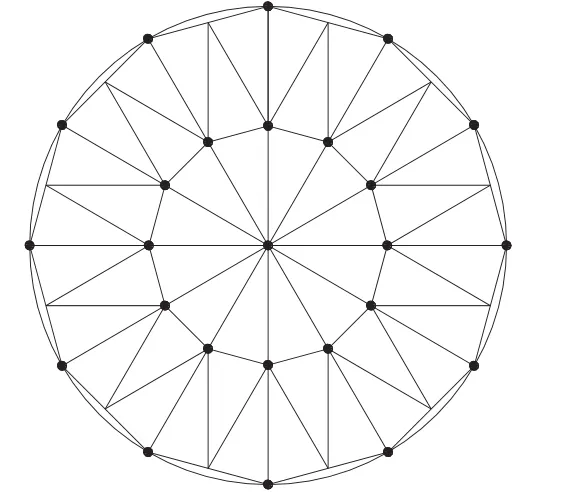
图6 球面网格化示意图

依照以上方法得到的每一个网格的各点对应的深孔轴线直线度误差为rWi；

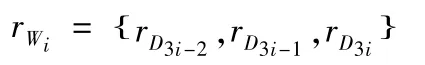
当满足以下条件时停止搜索，将求得的最小外接圆作为直线度误差最终值，否则继续搜索。

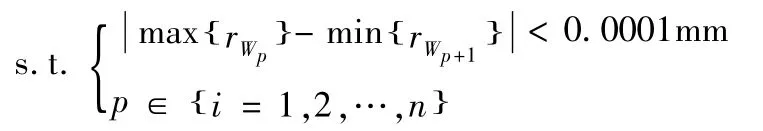
（2）将点集A′k向xy面投影

求解点集A′k在xy面上的投影，得到点集A″k，其变换短阵为T。

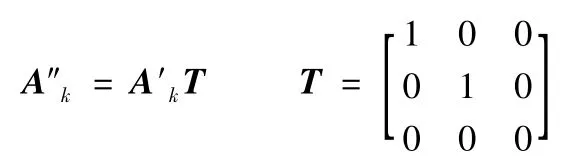
（3）求解点集A″k的最小外接圆

凸壳为包含点集A″k的最小凸多边形，确定最小外接圆的点必然位于凸壳上，将凸壳上的点定义为有效点，有效点是确定最小外接圆的重要参考点，其余为可去除点［7］，凸壳上点的集合为C；

为了减小计算量，选择x，y方向上的四个极值点即连接（xmax，y）、（xmin，y）、（x，ymax）、（x，ymin）绘制凸壳，然后验证是否点集C的所有点都在凸壳内，如果存在点位于凸壳外，则改变凸壳连线，将该点增加到凸壳点集内。

最小外接圆的计算步骤如下［8-9］；

①以最小二乘法确定凸壳的初始圆心O1，记凸壳上点C1与圆心O1的最大距离为r1，以O1为圆心r1为半径作圆得到初始最小外接圆；

②沿O1C1方向移动圆心，半径逐渐减小直至点集C与圆的位置关系满足以下条件；

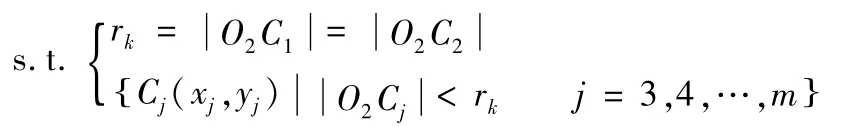
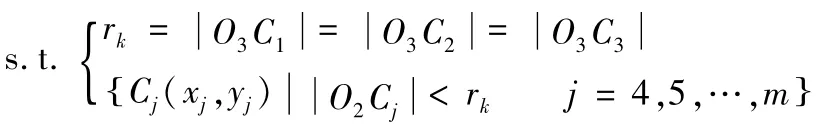
④判断C1、C2、C3的位置关系；

舍去钝角顶点，将其他两点定义为C1、C2，继续步骤③至搜索到满足条件的点。

（4）完成球面投影搜索后，依据最小条件原则对不同姿态下的点集投影的最小外接圆进行评估，确定深孔轴线直线度误差。

3 实验分析

文章以文献［10］中的数据作为参照进行直线度误差的评定，通过MATLAB编程运行评点方法，数据如表1所示。

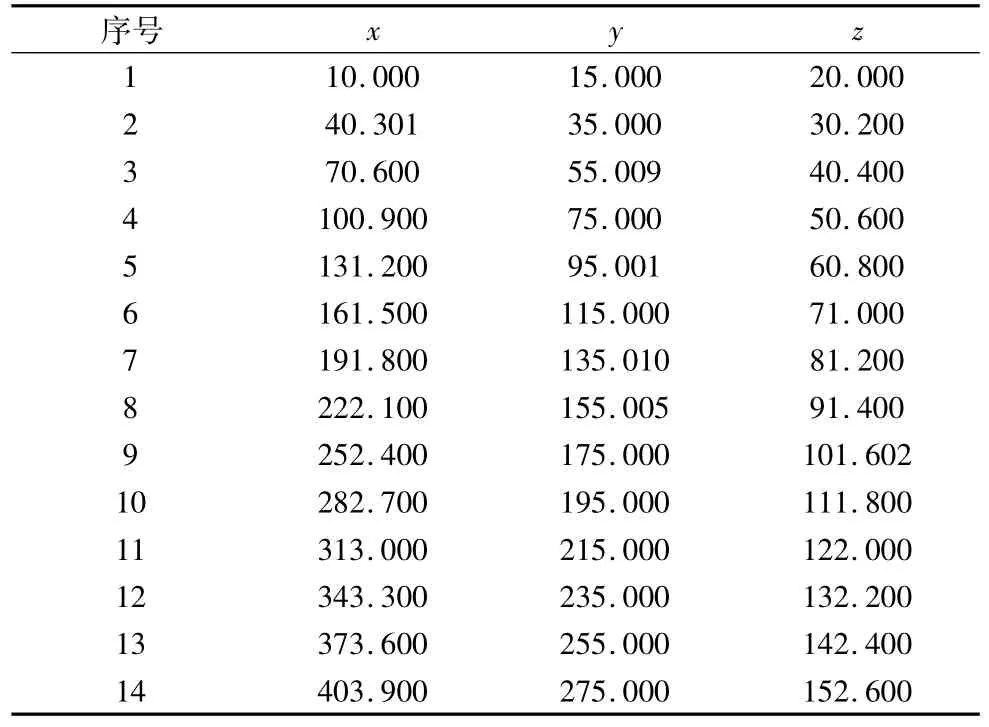
表1 空间离散点信息　单位：mm

取θ角为10°，依据以上数据得到球面方程f球面如下；

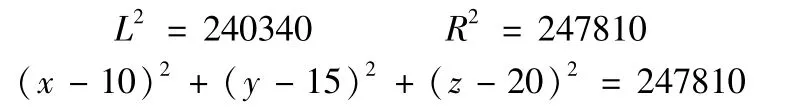
表1中14个点集的两端点连线的方向向量如下；

与两端点连线相垂直的空间平面f平面方程如下；393.9（x-403.9）+260（y-275）+132（z-152.6）=0

联立两个方程得到球面与平面相交圆f交圆，依据此圆求解网格细分点。

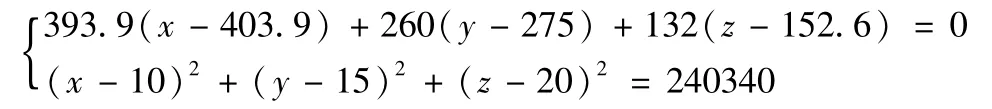
经计算平面f平面内过f交圆圆心的一条直线方程f直线如下；

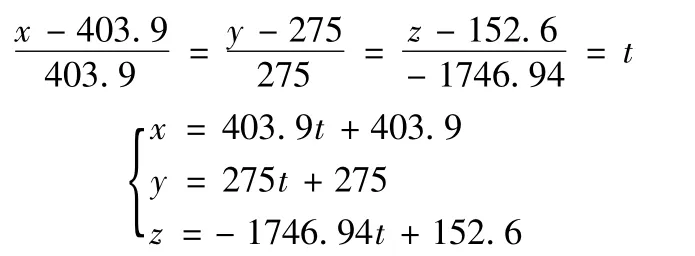
直线f直线与f交圆的两个交点坐标如下；

在f平面内过f交圆圆心且与f直线垂直的直线方程f垂线为；

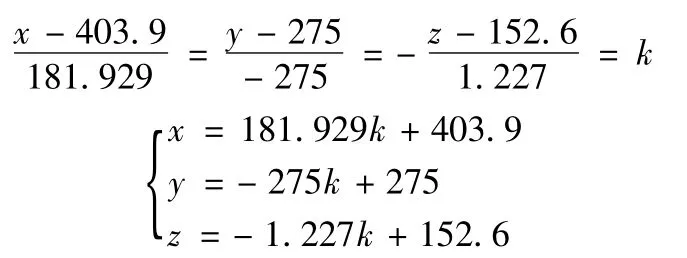
直线f垂线与f交圆的两个交点坐标如下；

依照以上方法对球面网格化，求得初始计算的球面上的8个点，其坐标如表2所示。

网格化过程依照上述8个点为基础依次求取球面上两点的中点进行投影求取深孔轴线的直线度误差，计算结果如表3所示［10-12］。最终求得的评定基线如下；

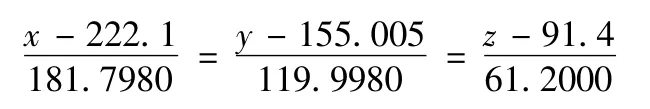
表2 网格化初始点　单位：mm

表3 各算法计算结果　单位：mm

依据计算结果可知球切面投影评定深孔轴线直线度误差的精度相较其他算法有一定的提高。

4 小结

球切面投影寻优评定深孔直线度误差与其他方案相比其特点如下；

（1）以直线度误差的评定基线的确定作为直线度误差评定的切入点，提高寻优效率，确定深孔直线度误差；

（2）将空间几何问题向平面转化，降低了直线度误差评定的检测对象的维度，减少了求解运算量，有利于计算速度的提高；

（3）利用网格逐次逼近法搜索最优解，相比遗传算法等智能算法不会丢失最优解，提高了搜索效率；

（4）最小外接圆的求解过程满足形状误差评定的最小条件准则，评定方案的理论误差小。

［1］王峻.现代深孔加工技术［M］.哈尔滨；哈尔滨工业大学出版社，2005.

［2］王世清.深孔加工技术［M］.西安；西北工业大学出版社，2003.

［3］米粮川，史玉彬，王鹏飞.身管直线度误差对弹丸初速跳角散布的影响［J］.弹道学报，2013（1）；94-98.

［4］廖平.基于遗传算法的形状误差计算研究［D］.长沙；中南大学，2002.

［5］郭松，李天毅，梅雪松，等.基于矩阵理论的直线度评定算法［J］.机械设计与制造，2004（1）；66-67.

［6］罗钧，王强，付丽.改进蜂群算法在平面度误差评定中的应用［J］.光学精密工程，2012，20（2）；422-430.

［7］张春阳，雷贤卿，李济顺，等.基于几何优化的圆度误差评定算法［J］.机械工程学报，2010，46（12）；8-12.

［8］林家春，石照耀.基于力学思想的最小外接圆度误差评定［J］.仪器仪表学报，2010，31（6）；1405-1410.

［9］郭仁忠著.空间分析［M］.北京；高等教育出版社，2001.

［10］廖平，喻寿益.基于遗传算法的空间直线度误差的求解［J］.中南工业大学学报，1998，29（6）；586-588.

［11］茅健，曹衍龙.基于粒子群算法的空间直线度误差评定［J］.工程设计学报，2006，13（5）；291-294.

［12］胡仲勋，杨旭静，金湘中.LSM算法评定空间直线度误差的分析与改进［J］.湖南大学学报（自然科学版），2010，37（2）；27-31.

（编辑 李秀敏）

Research on the Projection of Tangent Plane of Sphere for the Evaluation of Deep Hole Axis Straightness Error

LIShao-min1，2，YU Da-guo1，2，WANG Ji-ming1，2，HAO Yong-peng1，2
（1.School of Mechanical and Power Engineering，North University of China，Taiyuan 030051，China；2.Research Center of Deep-hole Machining Engineering Technology，Taiyuan 030051，China）

；A deep hole axis straightness errors assessment is proposed based on projection of tangent plane of sphere principle，tangent plane of sphere as the search path，the establishment of mathematical model of assessment deep hole axis straightness errors based on least contain are a method and mesh successive approximation；by point set projection，the space straight line evaluation is transformed into solve minimum circumscribed circle in the plane，by point set coordinate transformation to search for the optimal solution based on the line which perpendicular to the tangent plane of sphere，through sphere surface mesh successive narrow optimization range；the projection of tangent plane of sphere could provide a reference for determining straightness errors in any direction.

；deep hole；axis straightness；mesh successive approximation；projection；tangent plane of sphere

TH122；TG65

A

1001-2265（2015）05-0062-04 DOI：10.13462/j.cnki.mmtamt.2015.05.017

2014-12-19；

2015-01-24

国家自然科学基金资助项目（51175482）；山西省发明专利转化项目（141004）；中北大学科学基金资助项目（2012111）

李少敏（1988—），男，山西大同人，中北大学硕士研究生，研究方向为深孔加工及检测，（E-mail）lishaominmail@163.com。