曲轴随动磨削中误差建模与变形影响因素研究*

曹成真，姚振强，张雪萍，覃建芳，潘赐钰

（1.上海交通大学机械与动力工程学院，上海 200240；2.上汽通用五菱汽车股份有限公司，广西柳州 545027）

曲轴随动磨削中误差建模与变形影响因素研究*

曹成真1，姚振强1，张雪萍1，覃建芳2，潘赐钰2

（1.上海交通大学机械与动力工程学院，上海 200240；2.上汽通用五菱汽车股份有限公司，广西柳州 545027）

结合随动磨削过程中曲轴和砂轮的运动特点，通过理论分析建立了连杆颈直径尺寸的误差分析模型。同时利用有限元仿真和MATLAB计算，分析随动磨削中连杆颈的受力变形规律和影响连杆颈直径尺寸的因素，从而实现对连杆颈磨削精度的控制。理论计算表明，在力的综合作用下，连杆颈的变形呈现出以360°为周期的周期性；磨削力和中心支架力是影响连杆颈直径尺寸的因素，顶尖力不影响连杆颈的直径。最后通过随动磨削实验验证了误差分析模型和理论分析的正确性。

随动磨削；连杆颈直径；误差建模；力的影响

0 引言

曲轴是发动机中六大关键零部件之一，其加工精度直接影响发动机的压缩比和摩擦功等性能［1］。在对曲轴连杆颈进行加工时，现在的加工工序主要包括随动铣削、随动磨削、抛光、清洗等［2］。其中，随动磨削过程完成连杆颈的精加工，是决定连杆颈加工精度的关键工序。

在曲轴的加工中，影响加工精度的因素比较多。杨宪等［3］研究了中心支架压力和顶尖力对曲轴主轴颈直径、圆度和圆跳动的影响；丁利强等［4］研究了中心架支撑位置对主轴颈磨削精度的影响；周志雄等［5］对连杆颈随动磨削过程中曲轴的刚度误差进行了分析，并在恒磨除率条件下给出了曲轴刚度误差补偿公式；田应仲［6］分析了影响曲轴连杆颈随动磨削精度的因素，并对机床伺服跟踪误差、砂轮磨损等因素对连杆颈磨削精度的影响进行了理论分析；周杰等［7］研究了砂轮架直线电机的插补周期、工件转速和工件最小分度角对连杆颈圆度的影响。但以上的分析与研究主要针对实际生产中影响主轴颈磨削精度的误差因素和理论中影响连杆颈磨削精度的误差因素，对实际生产中影响连杆颈磨削精度的误差因素连杆颈受力变形规律的研究较少。

以某厂生产的四缸曲轴为研究对象，通过理论分析建立连杆颈直径尺寸的误差分析模型；同时利用有限元仿真和MATLAB计算，分析随动磨削中连杆颈的受力变形规律和影响连杆颈直径尺寸的因素，为曲轴的实际生产提供指导。

1 连杆颈随动磨削直径尺寸误差分析模型

曲轴连杆颈的磨削过程是随动磨削过程，磨削过程中曲轴和砂轮按照一定的规律运动。在随动磨削过程中，曲轴会受到重力、磨削力、中心支架力、顶尖力、卡盘力的综合作用。由于曲轴形状复杂，再加上曲柄半径的存在，使得随动磨削过程中曲轴容易变形，其在磨削过程中的装夹如图1所示。

图1 随动磨削过程中曲轴装夹示意图

在力的综合作用下，连杆颈的受力变形如图2所示。连杆颈的轴心由Ow点移动到Ow′点，设Ow点的坐标是（x，y），Ow′点的坐标是（x′，y′）。不考虑砂轮进给误差，并在砂轮是刚体的假设前提下，受力前后砂轮中心 Os点的坐标保持不变，设为（a，0）。在△OOw′Os中，利用三角形的正余弦定理，可以求得磨削切点N′至连杆颈中心Ow′的距离，即线段Ow′N′的长度。

图2 连杆颈在磨削过程中的受力变形示意图

随动磨削过程中，在图2所示的OXY坐标系下，连杆颈理论位置的轴线中心坐标为；

其中，R为曲柄半径理论长度。

曲轴受力变形后，连杆颈实际位置的轴线中心坐标为；

其中，Δx、Δy是连杆颈轴线中心相对于其理论位置的在X轴和Y轴方向的变形量。

则在△OOw′Os中，边OOw′的长度为；

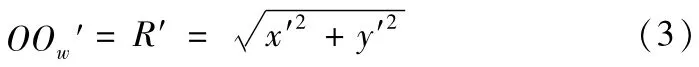
边Ow′Os的长度为；

边OOs的长度为；

∠Ow′OOs的大小为；

∠OOsOw′的大小为；

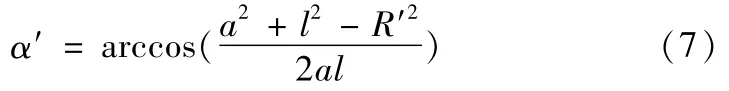
∠B′Ow′Os的大小为；

线段Ow′N′的长度为；

其中，Rs为砂轮半径。

为了分析影响连杆颈直径尺寸的因素，需要建立以连杆颈实际位置的轴线中心Ow′为坐标原点的Ow′mn坐标系，如图3所示。

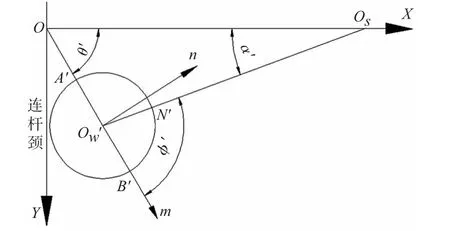
图3 以Ow′为坐标原点建立的局部坐标系

在局部坐标系Ow′mn中，实际磨削切点N′的坐标是；

这样，就建立了连杆颈实际磨削切点N′的坐标与曲轴转角θ之间的关系，结合有限元仿真计算得到的曲轴在力的综合作用下的变形数据，就可以利用最小二乘法对影响连杆颈直径尺寸的因素进行理论分析。

2 随动磨削中连杆颈受力变形的仿真计算

随动磨削过程中，曲轴受到磨削力、顶尖力、中心支架力、重力和卡盘力的作用，连杆颈轴线的变形比较复杂，故采用有限元仿真的方法对连杆颈的变形进行计算。

利用Solidworks软件建立曲轴的三维模型；在Hypermesh软件中对曲轴的三维模型进行网格划分；最后利用Abaqus软件对已经完成网格划分的曲轴模型进行力和位移的边界条件的加载，并计算连杆颈在随动磨削过程中的受力变形。

在随动磨削过程中，磨削切点N的位置随曲轴转角θ的改变而发生变化，如图4所示。同时，磨削力的大小和方向也是随着曲轴转角θ而周期性变化的。在对随动磨削过程中连杆颈的受力变形进行有限元仿真计算时，曲轴转角每隔30°建立一个仿真计算模型，在曲轴转动一周，即360°，的过程中，共建立12个仿真计算模型。在这12个仿真计算模型中，随着曲轴转角θ的不同，施加不同的力的边界条件，来模拟随动磨削的动态加工过程。

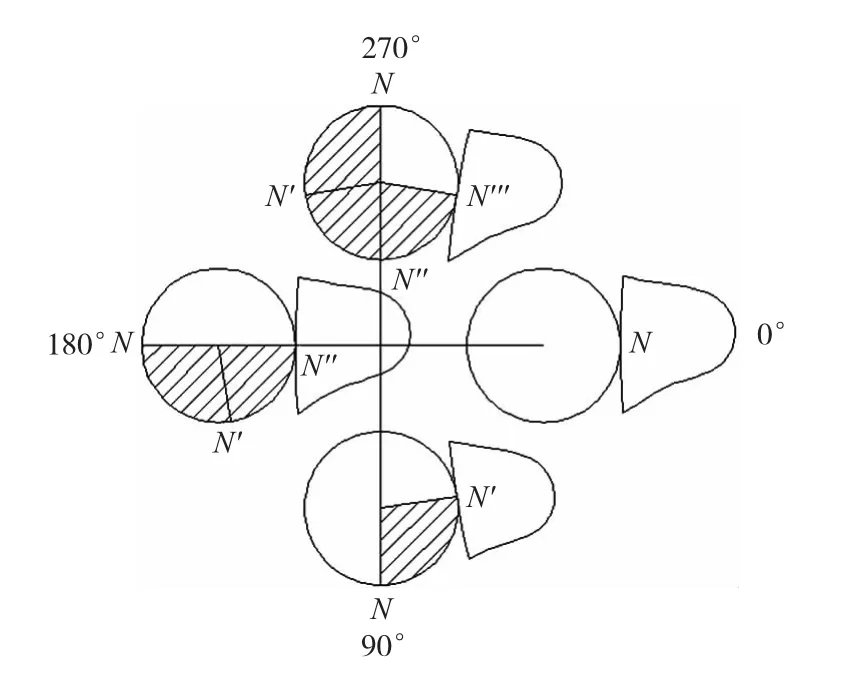
图4 随动磨削过程中磨削切点变化示意图

为了在不同的曲轴转角θ下能够更准确地施加力的边界条件，利用该四缸曲轴的几何参数，计算出磨削切点处法向磨削力与水平方向的夹角，如图5所示。通过运动分析的方法得到了磨削切点在连杆颈表面和砂轮表面的运动速度的表达式［8］；利用Hertz弹性变形理论对砂轮和磨粒在磨削过程中的变形进行分析，得到了磨削过程中的接触弧长的表达式［9］；通过利用布氏硬度值的测量原理对单颗磨粒的受力进行计算［10］，结合接触弧长和切点跟踪磨削法中磨削切点在连杆颈表面和砂轮表面的运动速比，建立的切点跟踪磨削法磨削力计算模型计算得到不同曲轴转角θ下的法向磨削力和切向磨削力，如表1所示。

图5 随动磨削切点处磨削力接触角示意图

中心支架、顶尖、每只卡爪（四爪卡盘）均是采用液压驱动，利用压强乘以液压缸作用的面积可求得三个力的大小为；Fzhijia=113.66N，Fdingjian=142.55N，Fkapan=1544.71N。重力始终指向地面。

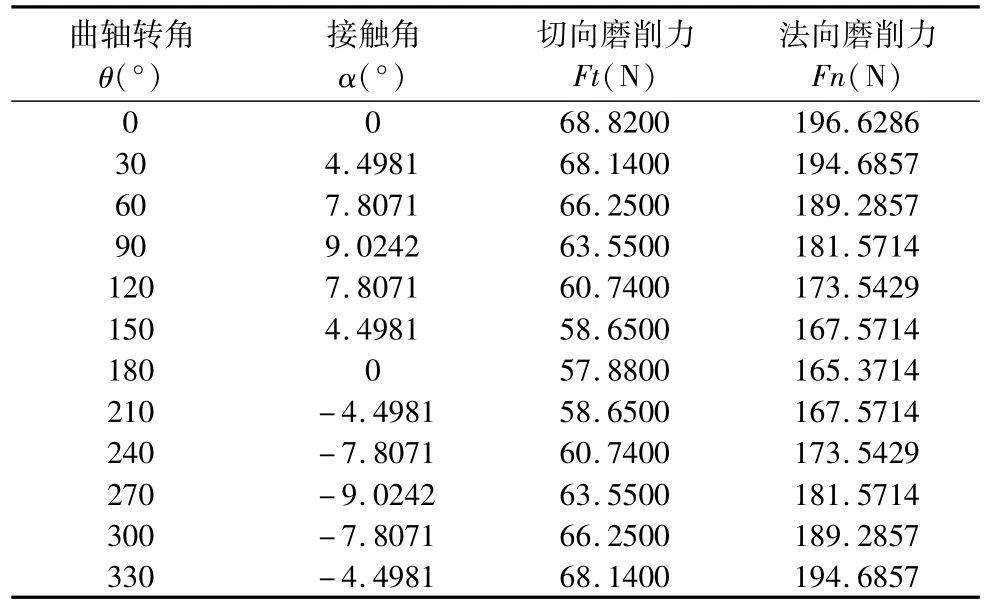
表1 不同曲轴转角下的磨削力

针对所研究的曲轴，在有限元模型中，曲轴的材料和特性参数的取值如表2所示。

表2 曲轴的材料和特性参数

将材料的特性参数赋予有限元模型，并将磨削力、中心支架力、顶尖力、卡盘力和重力按照不同的曲轴转角θ施加到相对应的位置上，在曲轴法兰端约束3个移动自由度，在曲轴芯轴端约束2个移动自由度，所建立的有限元分析模型如图6所示。

图6 曲轴的有限元分析模型

利用Abaqus软件计算所有力作用下的连杆颈的径向变形和切向变形如图7、图8所示。

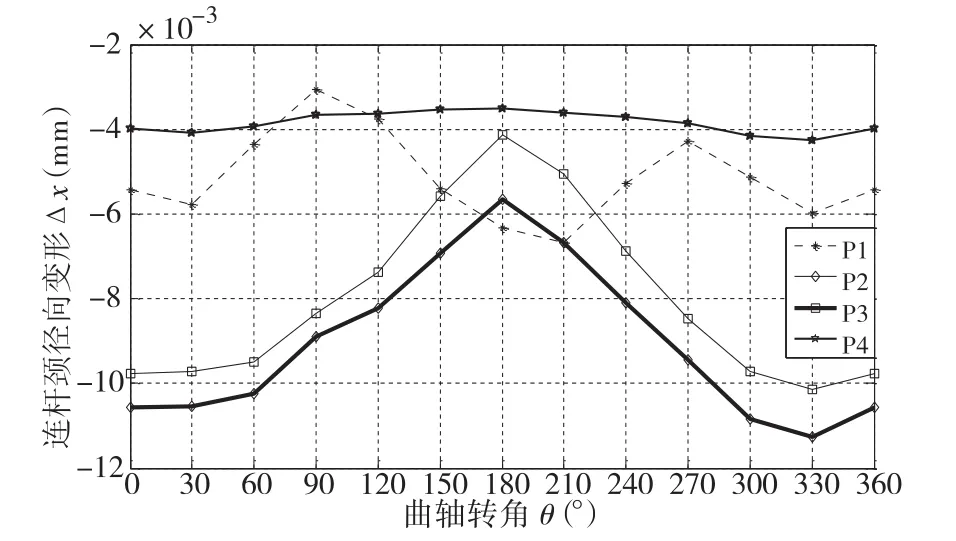
图7 力综合作用下连杆颈的径向变形Δx

图8 力综合作用下连杆颈的切向变形Δy

从图7和图8中可以看出，在力的综合作用下，连杆颈的径向变形和切向变形均呈现出以360度为周期的周期性特点；连杆颈径向变形规律较为复杂，在曲轴转角θ为180°时，径向变形量较小；切向变形规律呈现出正弦特征。

采用傅里叶级数对仿真数据进行拟合，可以得到在力的综合作用下各个连杆颈的径向变形量Δx与曲轴转角θ之间的关系式，同理可得切向变形量Δy与曲轴转角θ之间的关系式。将Δx、Δy的数值带入到连杆颈直径误差分析模型中，可以分析随动磨削过程中影响连杆颈直径的因素。

3 理论分析影响连杆颈直径的因素

以第二连杆颈P2为例，将有限元仿真计算得到的P2的径向变形值Δx和切向变形值Δy的拟合数值带入到连杆颈直径尺寸的误差分析模型中，每间隔1°取点，并将变形值放大100倍，可以得到P2的实际磨削轨迹如图9所示。

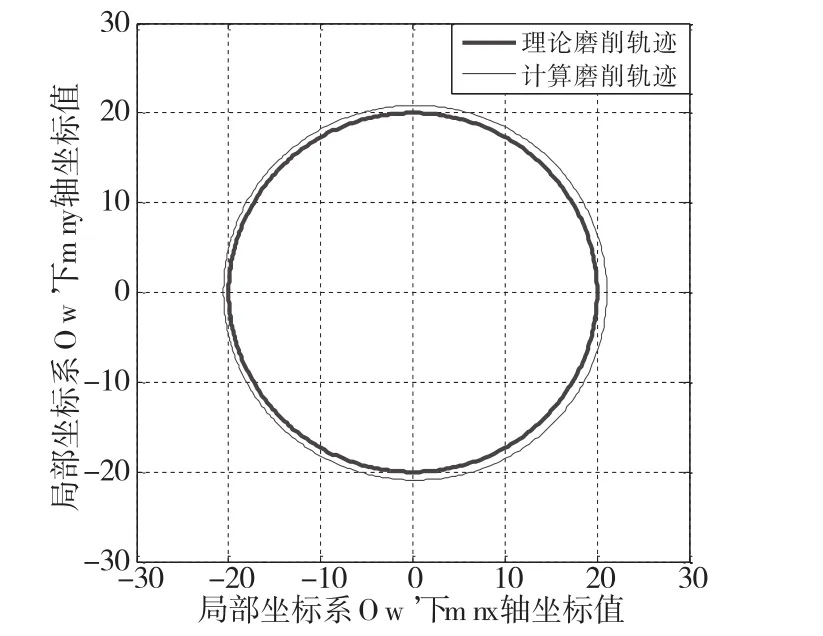
图9 变形值放大100倍后的连杆颈磨削轨迹

从图9中可以看出，在力的综合作用下，连杆颈的计算磨削轨迹发生了改变，连杆颈的直径变大，且随着曲轴转角的改变连杆颈直径增大的值并不一致。

结合有限元仿真计算得到的变形数值，利用最小二乘法计算连杆颈的直径，并在MATLAB程序中先后将磨削力、中心支架力、顶尖力减小20%，计算得到的连杆颈的直径的变化如图10所示。

图10 不同力边界条件下P2直径的变化

当磨削力减小20%时，P2直径减小6.2μm；当支架力减小20%时，P2直径增大2.8μm；当顶尖力减小20%时，P2直径不变。在磨削过程中重力和卡盘力不能改变，故不予进行对比。

由此可见，磨削力、中心支架力是影响随动磨削中连杆颈直径尺寸的主要因素。

4 影响连杆颈直径尺寸因素的实验验证

为了对随动磨削过程中连杆颈直径尺寸的误差分析模型及理论分析进行验证，设计了一个以磨削力和中心支架压力为变量的实验，实验中两个变量各取三个水平。由于磨削力不能直接改变，故通过改变磨削过程中的砂轮的线速度来改变磨削过程中的磨削力的大小。针对所研究的曲轴磨削时的条件，计算得到砂轮线速度与随动磨削过程中的平均磨削力之间的关系如图11所示。

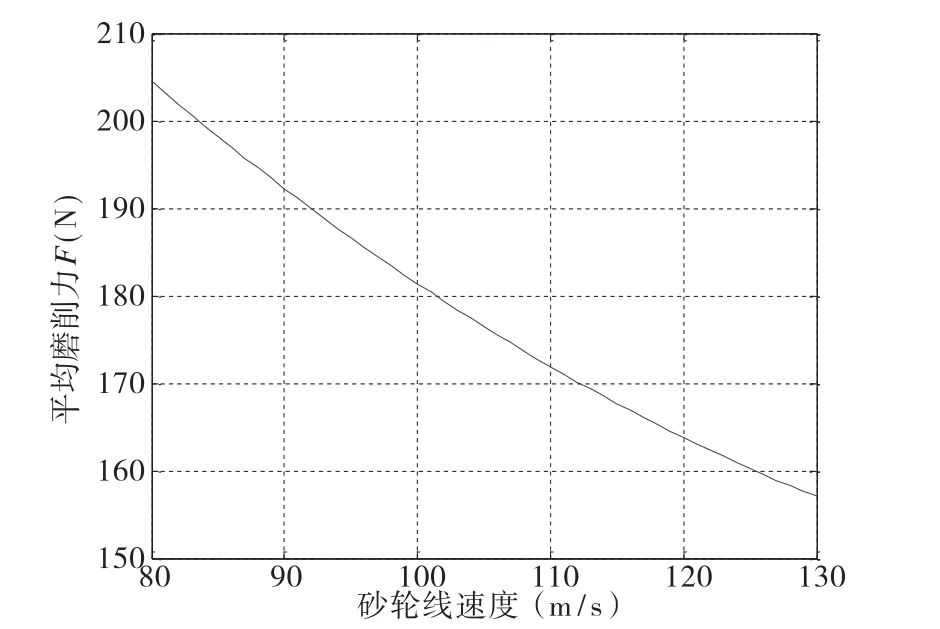
图11 计算得到的砂轮线速度与磨削力的关系

不考虑两个变量间的交互作用，所设计的实验的具体参数如表3所示。

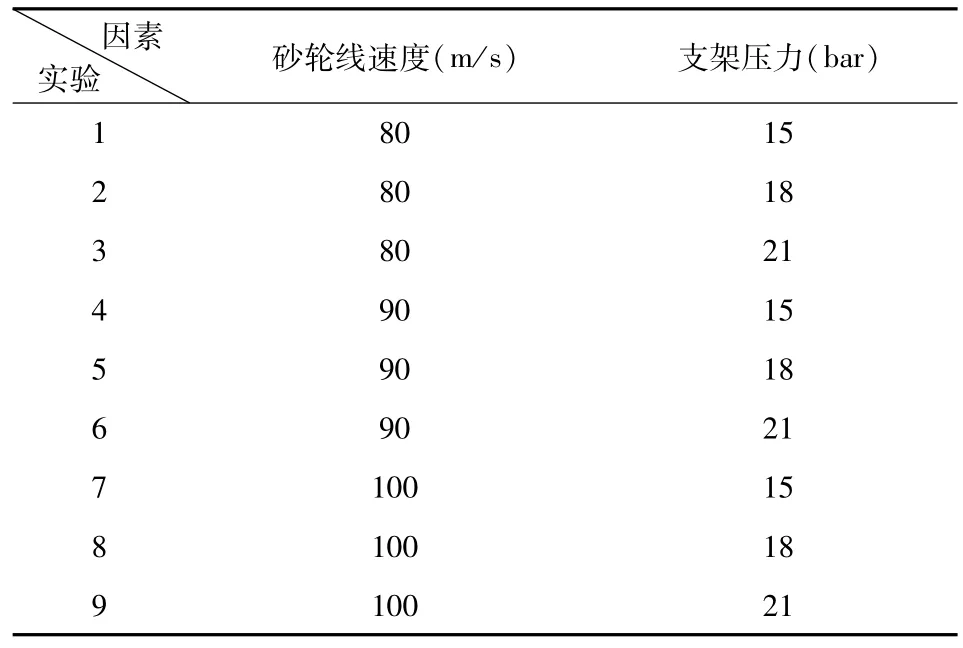
表3实验参数表

采用MARPOSS测量装置对磨削后的连杆颈的尺寸进行测量，并提取P2的直径尺寸进行分析。用Ai表示砂轮线速度（m/s）（i=1，2，3），用Bj表示中心支架压力（bar）（j=1，2，3），用Xij表示磨削后的第2连杆颈直径（mm），则实验结果如表4所示。

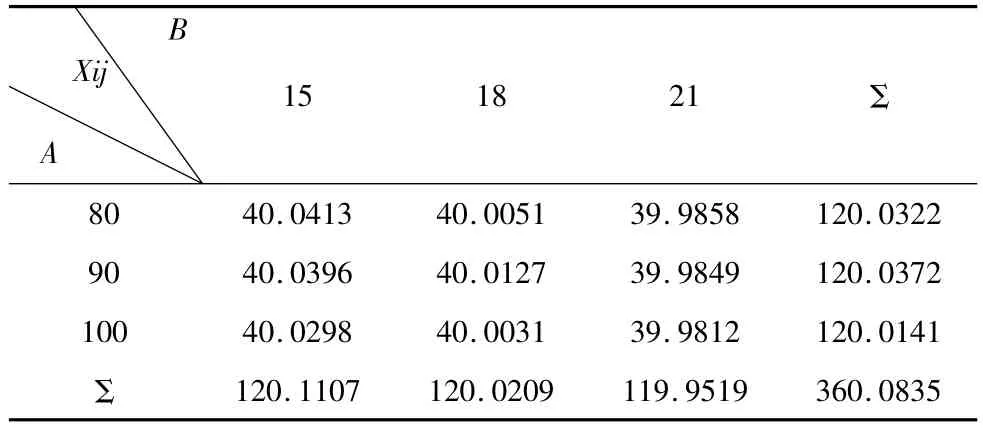
表4 第2连杆颈直径尺寸测量结果

通过双因素方差分析，计算得到砂轮线速度的检验统计量FA=4.72，中心支架压力的检验统计量FB=202.59。取显著性水平α=0.1，F0.1（2，4）= 4.32。通过两个因素的检验统计量与F0.1（2，4）的值的比较，可以得到，砂轮线速度和中心支架压力都是影响随动磨削过程中连杆颈直径尺寸的因素。

5 结论

（1）结合随动磨削过程的特点，通过理论分析建立了随动磨削过程中连杆颈直径尺寸误差分析模型，用于对实际磨削过程中曲轴受力后影响连杆颈直径尺寸的因素的理论分析。

（2）利用有限元仿真计算的方法，结合随动磨削过程中曲轴和砂轮的运动特点，对随动磨削过程进行仿真。由于随动磨削是一个动态的过程，采用每隔30°建立一个有限元计算模型，并根据曲轴和砂轮的接触位置的不同施加力的边界条件，计算不同曲轴转角下连杆颈的变形。变形数据显示，在力的综合作用下，连杆颈的径向变形和切向变形均呈现出以360°为周期的周期性特点；连杆颈径向变形规律较为复杂，在曲轴转角θ为180°时，径向变形量较小；切向变形规律呈现出正弦特征。

（3）利用仿真计算得到的连杆颈在随动磨削过程中的变形数据进行数据拟合，通过连杆颈直径尺寸误差分析模型理论分析了影响连杆颈直径尺寸的因素，并通过实验对理论分析进行了验证。验证结果表明，磨削力和中心支架压力是影响连杆颈直径尺寸的因素，证明了连杆颈直径尺寸误差分析模型和理论分析的正确性，对曲轴连杆颈磨削精度控制具有指导意义。

［1］钟明明.发动机制造精度与性能关系研究［D］.上海；上海交通大学，2012.

［2］郭力，李东超.国内外曲轴磨削加工工艺发展趋势［J］.精密制造与自动化，2013（1）；48-51.

［3］杨宪，姚振强，宋凤敏，等.曲轴磨削误差分析与精度控制方法［J］.机械设计与研究，2014（4）；99-103.

［4］丁利强，张雪萍，姚振强.汽车曲轴的磨削精度控制［J］.机械设计与研究，2013（6）；66-69.

［5］周志雄，罗红平，许第洪，等.切点跟踪磨削法中工件的刚度误差分析及其补偿［J］.机械工程学报，2003（6）；98-101.

［6］田应仲.曲轴非圆磨削表面几何形状误差及其在线测量方法的研究［D］.上海；上海大学，2007.

［7］周杰，刘学平，段广洪，等.曲轴切点跟踪磨削法控制误差分析研究［J］.机械设计与制造，2012（12）；7-9.

［8］T.Fujiwara，S.Tsukamoto，M.Miyagawa.Analysis of the Grinding Mechanism with Wheel Head Oscillating Type CNC Crankshaft Pin Grinder［J］.Key Engineering Materials. 2005，291-292；163-170.

［9］W B Rowe，H SQi，M N Morgan，et al.The real contact length in grinding based on depth of cut and contact deflections，in；Proceedings of the Thirtieth International MATADOR Conference［C］.UMIST，New York；Macmillan Press，1993.

［10］R L Hecker，S Y Liang，Xiao Jian Wu，et al.Grinding force and power modeling based on chip thickness analysis［J］.International Journal of Advanced Manufacturing Technology，2007，33；449-459.

Error Modeling and Force Effects Analysis on Crankshaft Pin Diameter in Path Controlled Grinding

CAO Cheng-zhen1，YAO Zhen-qiang1，ZHANG Xue-ping1，QIN Jian-fang2，PAN Ci-yu2
（1.School of Mechanical Engineering，Shanghai Jiao Tong University，Shanghai 200240，China；2.SAIC GM Wuling Automobile Cooperation Ltd.，Liuzhou Guangxi545027，China）

；Under the kinematic analysis in path controlled grinding process，an error analysis model on crankshaft pin diameter is established through theoretical analysis.The deformation pattern caused by forces during path controlled grinding process and the factors which affect the grinding precision of crankshaft pin diameter are analyzed with finite element simulation and MATLAB calculation methods，in order to achieve accurate control of crankshaft pin in path controlled grinding process.The theoretical calculation results show that the deformation of crankshaft pin occurs at360 degree cycle，it is the grinding force and work rest pressure that affect the diameter of crankshaft pin，and the top pressure does not affect the diameter of crankshaft pin.The model and the theoretical calculation results are validated by the experiment of crankshaft pin′s path controlled grinding.

；path controlled grinding；crankshaft pin diameter；error modeling；force effects

TH161；TG65

A

1001-2265（2015）05-0050-04 DOI：10.13462/j.cnki.mmtamt.2015.05.014

2014-08-09

汽车发动机制造精度控制的″两微米″工程（2012BAF06B03）

曹成真（1989—），男，山东菏泽人，上海交通大学硕士研究生，研究方向为汽车发动机曲轴随动磨削工艺，（E-mail）mengxiangchengzhen01@126.com。