基于EMD的主轴振动信号去噪方法研究*
籍永建,王红军
(北京信息科技大学a.现代测控技术教育部重点实验室;b.机电工程学院,北京 100192)
基于EMD的主轴振动信号去噪方法研究*
籍永建a,b,王红军a,b
(北京信息科技大学a.现代测控技术教育部重点实验室;b.机电工程学院,北京 100192)
主轴的振动信号中包含了大量与主轴运行状态相关的信息,由其合成的轴心轨迹具有很高的研究价值。合理的去噪方法能够得到更加有效的信号成分,有助于对主轴的工作性能做出正确的判断。与传统的去噪方法对比,基于EMD的去噪方法具有较强的自适应性。介绍了EMD去噪的基本原理并将其与传统的小波去噪方法进行对比,结果表明EMD的去噪效果更好。将EMD运用到主轴振动信号的降噪中,得到主轴去噪后的轴心轨迹。
主轴;振动信号;轴心轨迹;EMD去噪;小波去噪
0 引言
主轴的振动位移信号中包含了大量的信息,通过振动位移信号合成的轴心轨迹可以判定主轴的运行状态以及对数控机床做进一步的深入研究。然而在采集信号的过程中不可避免的会掺杂着噪声信号,去噪效果的好坏直接影响着对主轴工作状态的评价以及后续的研究。传统的去噪方法主要是通过滤波器滤掉噪声频率部分,但这类方法在处理混有白噪声、非平稳的信号时存在一定的局限性,对信号进行降噪处理实际上是抑制信号中的无用成分,重构信号中的有用部分[1]。EMD在去噪方面具有较强的自适应性,可以从数据中自适应的得到基函数,避免了小波去噪方法中由于基函数的选取不当对降噪效果的影响。
1 经验模态分解(EMD)
1.1 EMD简介
EMD算法将复杂信号分解成若干本征模函数(IMF)之和。IMF分量必须满足两个条件[2]①对于该分量信号,其极值点和过零点数目必须相等或至多相差一个;②在任意点处,局部最小值的包络线和局部最大值的包络线平均值为零[3]。其具体分解步骤[4]如下所述。
(1)找出信号中所有的局部极大值点,用三次样条插值将所有极大值点连接起来形成上包络线,同理将所有极小值点形成下包络线。
(2)求出上、下包络线的平均值m(t),原始信号x(t)与m(t)的差值记为h(t),如果h(t)满足IMF的条件,则h(t)是原始信号x(t)的第一个IMF,否则把h(t)作为原信号,重复步骤(1)、(2),直到得到的差值满足IMF条件。利用标准差sD确定分离过程的结束条件[5],sD一般取0.2~0.3。
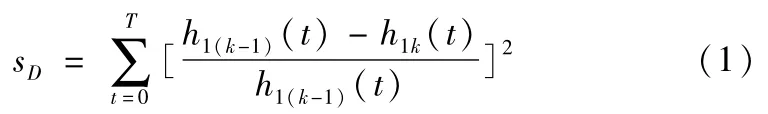
(3)将得到的第一个IMF分量记为c1,将c1从原始信号x(t)中分离出来,得到r1=x(t)-c1;
(4)将r1作为新的原始数据重复上述步骤,依次得到c2,c3...,直到rn呈单调趋势或非常小时停止。原始信号分解为
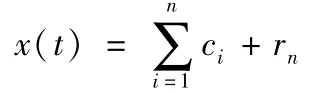
rn为残余函数。
1.2 EMD降噪原理
经过EMD处理后得到的一系列IMF分量中,随着分解阶数的增加,IMF的频率逐渐减小[6],信号的噪声部分主要集中在高频段,即前几个IMF中。原始信号经EMD处理后,可以通过选择合适的IMF分量进行重构以达到去噪的效果。但是,把某几个频段的IMF分量完全去除,属于强制去噪方法,这样会去除原信号中的有效成分,信号的完整性遭到破坏。在实际应用中,噪声与信号的频带往往是交互存在的,例如白噪声存在于整个频域内,此时便不能单纯地依靠重构某几个IMF分量达到去噪目的,运用门限去噪方法,对每一个IMF分量做阈值门限处理,然后再把处理后的信号进行重构。
EMD阈值滤波的思路是为每一个IMF分量设定一个阈值,利用该阈值对各IFM分量进行去噪处理。然后对去噪后的IMF分量进行重构,得到去噪信号。
2 EMD去噪在实际工程中的应用
2.1 数据的采集
采用美国Lion公司生产的主轴误差分析仪(SEA)采集某数控机床运行时主轴的振动位移信号。设置采样频率4096Hz。利用两个成直角布置的电容传感器采集主轴X,Y方向的振动信号。数据采集现场如图1所示。

图1 数据采集现场
2.2 信号的分解
对所采集的信号进行EMD处理,得到11个IMF分量和一个残余量,前7个IMF分量如图2所示。

图2 EMD处理后得到的IMF
由图2可以看出采集的信号经过EMD处理后,分解为一系列频率由高到底的IMF分量,前几个IMF为高频信号,其中含有大量的噪声信号,由上到下,IMF的频率依次降低。
2.3 信号的降噪处理
2.3.1 阈值函数的选取
为了验证EMD降噪方法的有效性。采用小波阈值降噪方法与其进行对比。选取的小波基函数为db6,分解层数为6。小波去噪选用的阈值函数如式(2)。

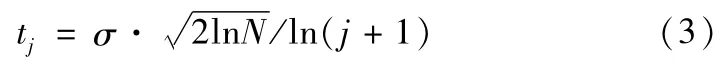
EMD阈值去噪方法选用的软阈值函数如式(4)。

2.3.2 信号处理
对每个IMF分量进行阈值去噪处理,然后再重构信号。由采集的振动位移信号合成的主轴原始轴心轨迹与降噪后合成的轴心轨迹如图3所示。

图3 轴心轨迹图
由图3可以看出,小波去噪方法与EMD去噪方法对采集的信号都起到了去噪的作用,但是哪种方法效果更好,需要用一些指标来评定。常用的去噪效果评价指标有均方根误差(RMSE)[9],其值越小去噪效果越好;信噪比(SNR)[10],信噪比高表明去噪效果好;平滑度(r)指标[11],其值越小去噪效果越好。评定结果如表1所示。
由表1可以看出,小波去噪方法的均方根误差值小于EMD方法,但是EMD方法的信噪比与平滑度指标均优于小波方法,总体看来,EMD的去噪效果优于论文中所用的小波阈值方法。

表1 两种方法对应的去噪效果评价指标
3 结论
介绍了经验模态分解(EMD)以及去噪原理,将其运用到主轴振动位移信号的去噪中,并利用小波阈值算法对同一组信号进行去噪处理,将两种去噪方法的去噪效果进行对比,结果表明EMD方法的去噪效果更好,能保证有用信号的完整性,更适合对采集的振动信号进行去噪处理。
[1]张翀.基于EMD去噪方法研究[J].电脑知识与技术,2010,6(35);10113-10115.
[2]万鹏.基于流形学习的主轴系统故障诊断方法研究[D].北京;北京信息科技大学,2012.
[3]胡劲松.面向旋转机械故障诊断的经验模态分解时频分析方法及实验研究[D].杭州;浙江大学,2003.
[4]杨志华,齐东旭,杨力华,等.一种基于HHT的信号周期性分析方法及应用[J].中山大学学报(自然科学版),2005,44(2);14-18.
[5]吴虎胜,吕建新,来凌红,等.基于EMD-SVD模型和SVM滚动轴承故障模式识别[J].噪声与振动控制,2011(2);89-93.
[6]Cherneva Z,Guedes Soares C.Local non-stationary properties of the wind wave groups[C].Proceedings of the conference on design and operation for abnormal conditions II.London;Royal Institution of Architects,2001;137-45.
[7]刘恒冰,韩世勤,刘晶.基于新阈值函数及最优尺度的小波去噪研究[J].计算机工程与应用,2007,43(24);72-74,113.
[8]赵雯雯,曾兴雯.一种新的EMD去噪方法[J].电子科技,2008(5);30-32,36.
[9]文鸿雁.基于小波理论的变形分析模型研究[D].武汉;武汉大学,2004.
[10]吴富梅,杨元喜.基于小波阈值消噪自适应滤波的GPS/INS组合导航[J].测绘学报,2007,36(2);124-128.
[11]陶珂,朱建军.小波去噪质量评价方法的对比研究[J].大地测量与地球动力学,2012(2);128-133.
(编辑 李秀敏)(编辑 李秀敏)
Research of Denoising Method for Spindle Vibration Signal Based on Empirical M ode Decomposition
JIYong-jiana,b,WANG Hong-juna,b
(a.Key Laboratory of Modern Measurement&Control Technology;b.School of Mechanic and Electric Engineering,Beijing Information S&T University,Beijing 100192,China)
;Plenty of information related to the main shaft running state is contained in the spindle vibration signal,and reasonable denoising method can retain more effective signal components.The denoising method based on EMD has strong self-adaptability compared with traditional denoising methods.The basic principle of EMD de-noising is introduced and meanwhile the same vibration signal of spindle is purified by EMD Denoising method and Wavelet denoising method respectively,experimental results show that EMD Denoising method has great advantages in denoising.
;spindle;vibration signal;axis orbit;the EMD denoising;wavelet denoising
TH165;TG506
A
1001-2265(2015)05-0035-03 DOI:10.13462/j.cnki.mmtamt.2015.05.010
2014-08-10
北京市自然科学基金(KZ201211232039);国家自然科学基金(51275052);北京市高等学校人才强教(PHR201106132);PXM2014-014224-000080
籍永建(1986—),男,河北沧州人,北京信息科技大学硕士研究生,研究方向为机电系统故障诊断及预测,(E-mail)yongjian8701@163. com。

