基于ANSYS的浮置板轨道结构模态分析

李贵阔 廖英英 李向国

（石家庄铁道大学　 河北石家庄 050043）

基于ANSYS的浮置板轨道结构模态分析

李贵阔 廖英英 李向国

（石家庄铁道大学 河北石家庄 050043）

为对浮置板轨道结构参数进行动态优化设计，采用ANSYS软件中的缩减法对结构进行模态分析，研究结构的振动特性。在此基础上，详细分析浮置板长度、密度和钢弹簧支承间距、刚度4个结构参数变化对固有频率的影响。由分析结果可知，在满足结构相应要求的前提下，可以适当增加浮置板的长度、密度和钢弹簧支承间距，或者适当降低钢弹簧的刚度。

浮置板轨道 模态分析 振动特性 ANSYS

据中国轨道交通网统计，截止2014年底，中国共有37座城市获准修建城市轨道交通，其中22座城市已经开通运营的线路总里程达2 933.26公里。轨道交通蓬勃发展的同时，也带来了日益严重地振动与噪声问题。浮置板轨道结构具有较高的减振效果，对其进行振动频率分析，有着重要的现实意义。孙晓静等［1］建立列车——轨道结构二维耦合模型，讨论了系统振动特性以及钢弹簧刚度和阻尼对乘车舒适度和地基反力的影响。丁德云等［2］采用MIDAS/GTS软件建立三维有限元模型，选用子空间迭代法进行模态分析，研究了浮置板轨道结构参数对系统振动频率的影响。曹宇泽等［3］建立“车辆——轨道——隧道”空间有限元模型，分析了减振设计关键因素，对比了不同工下固有频率和减振性能。

本文采用ANSYS中的缩减法进行模态提取，该法适用于提取小到中等模型（小于10000个自由度）的所有模态。计算过程就是通过缩减模型矩阵的大小以实现快速简便的分析。缩减法一般需要预先人为定义自由度，而所选择的主自由度是否合适对结果很重要［4］

1 模态分析有限元模型及实体模型的建立

根据参考文献［2，5，6］，浮置板轨道结构模态分析基本参数选择如下：

钢轨：质量m=60 kg/m；弹性模量E=210 Gpa；泊松比0.3；钢轨容重7 960 kN/m3。浮置板：长×宽×高=24 m×3.0 m×0.5 m；密度2 500 kg/m3；弹性模量E= 32 Gpa。扣件：刚度50 kN/mm；阻尼50 kN·s/m；间距0.6 m。钢弹簧：刚度10 kN/mm；阻尼75 kN·s/m；横向中心间距2 m；纵向中心间距2 m。

建立浮置板轨道系统有限元模型时，既要如实地反映浮置板轨道系统实际结构的重要力学特性，又要尽量采用较少的单元和简单的单元形态，以保证有较高的计算精度和减少计算工作量。其计算结果的可信度直接受分析模型、模态参数、网格划分、约束条件等与实际的轨道结构力学特性符合程度的影响［3］。本文采用的浮置板轨道模型示意图如图1所示。

图1 浮置板轨道结构有限元模型

实体模型的建立：用三维梁单元BEAM188模拟钢轨，两个扣件之间的钢轨划分为一个梁单元；用实体单元SOLID45模拟浮置板；用弹簧阻尼单元COMBIN14来模拟扣件和钢弹簧。浮置板轨道结构实体模型如图2所示。

图2 浮置板轨道结构实体模型

考虑到模型沿线路中心线的对称性，本文取一半结构建立有限元模型，并进行结构的模态分析。施加约束时，在对称面上施加对称的边界条件；约束钢轨纵向位移；考虑剪力铰的存在，约束剪力铰处的竖向位移；在钢弹簧下部节点进行全约束。

2 钢弹簧浮置板的振动特性分析

模态分析用于确定结构的振动特性，即固有频率与振型，它们是承受动态荷载结构设计中的重要参数。当存在激振力作用时，可以得出结构产生共振的频率和各阶频率下的振型。模态分析的优点是系统的振动特性在设计阶段便可预知，进而指导结构参数的优化设计。

2.1 钢弹簧浮置板的固有频率

浮置板轨道结构属于质量—弹簧隔振系统。尽管浮置板具有很多高阶振动模态， 但当列车通过时对隔振效果起关键作用的是浮置板轨道系统的固有振动频率， 尤其是低阶固有频率［7］。

为了研究不同浮置板结构参数对结构固有频率的影响，首先选取以长24 m、密度2 500 kg/m3、弹簧支承间距2 m和钢弹簧刚度10 kN/mm等参数为基本工况。得到前六阶固有频率（如表1所示）。

表1 基本工况的前六阶固有频率

2.2 钢弹簧浮置板的振型

振型属于结构固有的振动特性，并与固有频率相对应。它不随测试方法和测试条件而改变。依据基本工况得出的振型如图3所示。

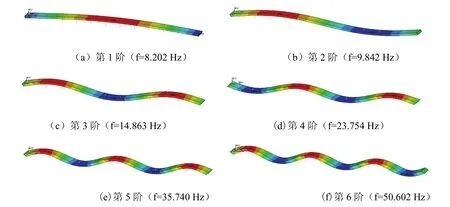
图3 浮置板在基本工况下的前六阶振型图

从图3可以看出，钢弹簧浮置板轨道结构的的前六阶振型主要以垂向弯曲为主。其中前两阶振型分别是由刚体平移和刚体转动而引起的振动形式。当浮置板轨道结构的参数发生变化时，系统的频率变化，但振型基本不变。图3中的振型揭示了系统的固有振动形态。

3 参数变化对浮置板轨道结构振动频率的影响分析

浮置板轨道振动频率主要受浮置板长度、密度和钢弹簧支承间距、刚度等结构参数影响，因此，有必要分析上述参数变化对浮置板轨道结构振动频率的影响。

浮置板长度和密度变化与系统固有频率的关系分别如图4、图5所示。

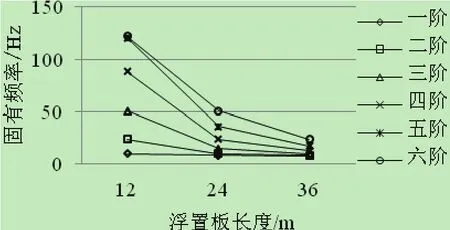
图4 浮置板长度与固有频率的关系

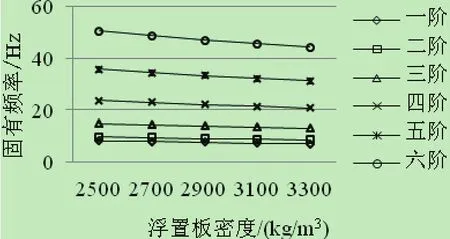
图5 浮置板密度与固有频率的关系

由图4知，当其他参数不变时，结构的振动频率随浮置板长度的增大而降低，高阶频率较低阶频率受到的影响更大。因此，在满足浮置板收缩变形前提下，可以适当增加浮置板的长度。

由图5知，当其他参数不变时，结构的振动频率随浮置板密度的增大而降低。因此，为了达到更好减振效果，在满足建筑限界的前提下，尽可能增加浮置板的密度。

钢弹簧支承间距和刚度变化与系统固有频率的关系分别如图6、图7所示。

由图6知，当其他参数不变时，结构的振动频率随钢弹簧支承间距的增大而降低。在满足变形协调条件以及其他安全性因素的条件下，可以适当增大钢弹簧支承间距。

由图7知，当其他参数不变时，结构的振动频率随钢弹簧刚度的增大而增大；低阶情况下减振效果相对高阶明显。因此，在满足结构动态变形限制下，可以适当降低钢弹簧刚度。

图6 钢弹簧支承间距与固有频率的关系

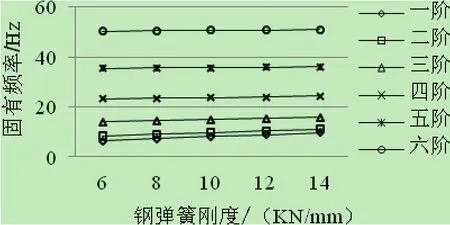
图7 钢弹簧刚度与固有频率的关系

4 结论

从模态分析的角度研究了浮置板结构的振动特性，分析了参数变化对浮置板轨道结构振动频率的影响规律，在以浮置板长度为24 m、密度2 500 kg/m3和钢弹簧支承间距2 m、刚度10 kN/mm等参数为基本工况的前提下，给出了浮置板轨道结构参数相应的取值建议：

（1）在满足浮置板收缩变形限值时，可以适当增加浮置板的长度；

（2）在满足建筑限界的前提下，尽可能增加浮置板的密度；

（3）在满足变形协调条件以及其他安全性因素的条件下，可以适当增大钢弹簧支承间距；

（4）在满足结构动态变形限制下，可以适当降低钢弹簧刚度。

［1］孙晓静，李术才，张敦福，等.车辆—钢轨—钢弹簧浮置板道床耦合系统振动特性分析［J］.山东大学学报，2011，41（3）：126～130

［2］丁德云，刘维宁，李克飞，等.钢弹簧浮置板轨道参数研究［J］.中国铁道科学，2011，32（1）：30～35

［3］曹宇泽，田苗盛，杨其振.隔离式橡胶浮置板减振性能研究［J］.铁道工程学报，2013（2）：34～38

［4］王新敏.ANSYS结构动力分析与应用［M］.北京：人民交通出版社，2014

［5］姚纯洁，郑玄东，肖安鑫.钢弹簧浮置板轨道结构静力学分析［J］.城市轨道交通研究，2012（2）：104～107

［6］赵留辉.地下线路浮置板轨道减振特性仿真分析［J］.铁道建筑，2014（8）：102～105

［7］梅早临，耿传智，梅早强，等.浮置板轨道结构振动模态分析［J］.城市轨道交通研究，2004（5）：54～56

Modal Analysis of Floating Slab Track Structure Based on ANSYS

LI Gui-kuo LIAO Ying-ying LI Xiang-guo

（Shijiazhuang Tiedao University Shijiazhuang 050043 China）

In order to optimize the floating slab track dynamic structure， the structure modal was analyzed with the help of the software of ANSYS and the reduction method and the vibration characteristic of the structure was studied. On the basis of this， the effects of the length and density of the floating slab and the spacing and stiffness of the steel spring on the natural frequency were analyzed. The results show that the length， density of the floating slab and steel spring bearing spacing should be appropriately increased or the stiffness of steel springs should be appropriately reduced with the demand of the floating slab track structure.

floating slab track modal analysis vibration characteristics ANSYS

文献标识码：A文章编号：1673-1816（2015）02-0067-04

2015-03-18

李贵阔（1986-），男，山东郓城人，硕士，研究方向轨道减振。

国家自然科学基金项目（11302137）；河北省自然基金项目（A2015210005）