新型混联式汽车电泳涂装输送机构多模型控制研究
高国琴,秦 天,方志明
(江苏大学 电气信息工程学院,镇江 212013)
0 引言
为克服现有汽车电泳涂装输送机采用悬臂梁结构的缺陷,本课题组研发了一种新型混联式汽车电泳涂装输送机构[1]。混联机构兼具串联机构和并联机构的优点,具有可控自由度高、工作空间大、速度快、刚性高等优点[2,3],但由于机构的复杂,提高了对其控制的要求和难度,为此,基于动力学模型的控制被引入到混联机构控制研究中[4,5]。然而,混联机构由于其闭链结构和运动学约束而使其整体动力学模型较为复杂,导致所设计控制系统往往难以满足其快速性要求[6]。
本文以本课题组最新研制的混联式汽车电泳涂装输送机构为研究对象,该混联机构的行走机构与升降翻转机构相对独立。升降翻转机构由翻转机构和升降机构组成。当翻转机构作用时,车体作翻转运动;当升降机构作用时,车体作升降运动。行走和升降运动复合使得车身在电泳槽中充分搅动,从而解决“空气包”问题,使车体100%表面都能泳涂上漆。车身在电泳液中的电泳时间是汽车电泳涂装的工艺参数之一,通常限定在2min~4min。在一定时间内,如果泳涂时间过长,涂膜则会增厚[7,8]。此外,汽车电泳涂装输送机构需实现进退、升降、翻转及其复合运动,因此具有多模式运动的特点。
针对上述新型混联式汽车电泳涂装输送机构的结构特点、多模式运动特点以及汽车电泳涂装的工艺要求,本文提出一种多模型控制方法,即将混联式汽车电泳涂装输送机构简化为不同工况的翻转系统和升降系统两个子系统,通过分别给两个子系统设计合适的控制器,以更好地满足该新型汽车电泳涂装输送机构的多运动模式要求,同时有效地提高混联式汽车电泳涂装输送机构在不同模式下运动控制的快速性。
1 运动学分析

图1 新型混联式汽车电泳涂装输送机构
新型混联式汽车电泳涂装输送机构如图1所示,该混联机构车体固定架与连接杆之间相互固定,车体通过夹具固定于车体固定架上。其升降翻转机构的结构简图如图2所示,该机构连接杆中心有两个主动输出,即一个移动输出和一个转动输出;其驱动运动副有六个,即四个移动输出和两个转动输出。
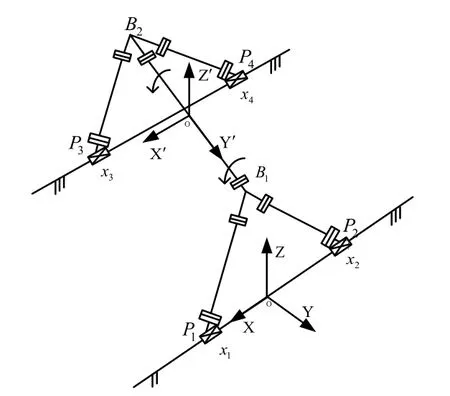
图2 升降翻转机构结构简图

图3 升降翻转机构运动学侧视图

图4 升降翻转机构运动学正视图
采用杆长长度约束方程,根据混联机构结构并结合冗余支链整理可得机构运动学逆解方程:

式中,L1为支杆长度,r1为从动轮半径,r2为主动轮半径,zi(i=1.2),βi(i=1,2)分别为升降翻转机构连接杆两端在静坐标系{B}的z轴位置和绕y轴逆时针转动的角度。
为了将广义力转化为关节驱动力,需求出雅各比矩阵。采用基于符号运算的微分变换法求解升降翻转机构的雅各比矩阵,即式(1)两端分别对时间求导并整理可得:
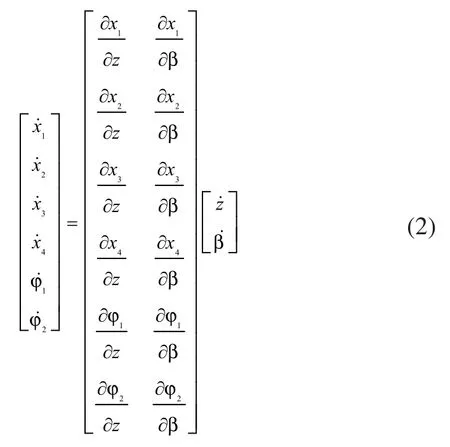
2 动力学分析
本文选择拉格朗日方法建立升降翻转机构的动力学模型。拉格朗日法是以系统动能和势能为基础建立动力学方程,推导过程比较简单,形式较为简洁,所建立动力学模型便于控制系统设计。拉格朗日函数L定义为系统的动能T和势能P之差,即L=T-P,其中T和P可以用任何方便的坐标系来表示,系统动力学方程[9,10],即拉格朗日方程为:

整理并建立标准动力学方程:

系统动能T包括车体动能TP、支链动能TL、传动动能TT以及滑块动能TS。即系统动能T为:

系统势能P包括车体势能PP、支链势能PL、传动势能PT以及滑块势能PS。即系统势能P为:

将式(5)和式(6)代入式(4)中并整理得升降翻转机构完整动力学方程为:
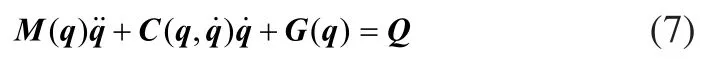
对机构整体动力学建模得完整动力学最终结果为:

式中,mp是被输送车体质量;ml1、ml2、ml3分别为连杆7、连杆11和连接杆16的质量;ml4是车体固定架17上支架的质量;m1、m2分别为第一滑块5和第二滑块9的质量;ma、mb分别为主动轮13与从动轮15的质量;a、b、c分别为车体长宽高;rl3为连接杆16的半径;r1、r2分别为从动轮15半径和主动轮13半径;L1、L2分别为连杆7和11的长度;L4为车体固定架17上斜支架的长度;θ为车体固定架17上两根斜杆之间的角度。
方程(7)具有以下性质:
1)M是对称且正定的;

考虑到汽车电泳涂装输送混联机构在实际工作过程中存在的各种外部干扰和摩擦力, 可得到如下形式的动力学模型:

从式(7)可见,新型混联式汽车电泳涂装输送机构具有较为复杂的动力学模型。为更好地实现新型输送机构实时动力学控制的工程应用,根据汽车电泳涂装工艺要求和输送机构特点,本文将复杂动力学模型简化为不同工况的两个子系统:翻转系统和升降系统。
翻转系统的动力学模型为:



升降系统的动力学方程为:
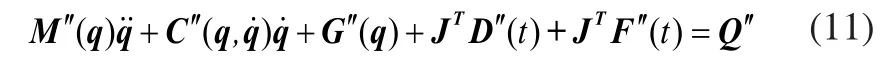

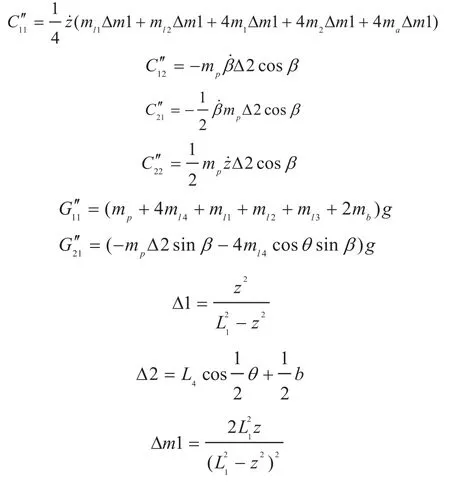
对新型混联式汽车电泳涂装输送机构,将其视为两个子系统分别建模,则子系统的动力学模型和整体动力学模型相比,其惯性矩阵和哥氏力、离心力项均得到了简化,为混联机构的动力学控制提供了简化的数学模型,并为进一步实现新型混联式汽车电泳涂装输送机构的高性能实际工程控制奠定了基础。
3 控制器设计
3.1 翻转子系统控制器设计
由于混联机构通过翻转运动输送车体进入槽液,在翻转过程中,被控对象的运动环境发生了较大变化,对于控制系统来说,若视其为外部扰动,则要求其具有较强的抗干扰能力,以保持翻转运动的平稳。滑模变结构控制具有响应速度快、对外部扰动不敏感、物理实现简单等特点[13],因此翻转子系统选用滑模变结构控制方法。
以混联机构连接杆中心点的位姿作为混联机构位姿,设其期望位姿为qd,以系统的位姿误差e和速度误差˙e作为状态变量,即:设计滑模面为:


基于动力学模型的滑模控制律设计如下:
首先对式(13)中的S求导,并将速度误差˙e和加速度误差˙˙e代入得:

由式(4)可得:

将式(15)代入式(14)得:
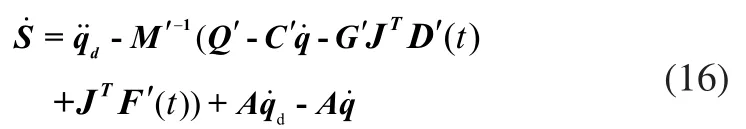

根据滑模控制基于函数切换控制的设计理论,设计翻转子系统控制律为:

下面证明所设计动力学滑模控制算法的稳定性。设Lyapunov函数为:

对式(19)求导可得:

其中:

将式(21)代入式(20)得:

根据Lyapunov稳定性定理,可见所设计动力学滑模控制算法稳定。
根据式(8),将广义驱动力转换为各关节驱动力F1为:

3.2 升降子系统控制器设计
汽车电泳涂装输送混联机构驱动白车身在电泳槽液里行走时,为消除其车顶气包,本课题组提出了驱动白车身进行小幅正弦轨迹运动的控制方案,因此需升降子系统驱动白车身作小幅度升降运动。在该运动过程中,控制的平稳性要求较高,而对控制的伺服精度要求并不高,因此本文研究采用基于动力学模型的计算力矩控制方式[14,15]。
计算力矩控制设计的基本思想是在控制回路中引入非线性补偿,使复杂的非线性控制系统化为更易于控制的线性定常系统,对于本系统而言,可以引入非线性补偿为:

消去非线性项后化为:

此外,设qd表示期望升降运动轨迹,定义跟踪误差为:

对式(26)求一次导为:

对式(26)求二次导为:


式中,Kd和Kp均为正定矩阵(为了计算方便可取为对角矩阵)。闭环系统方程为:

由Kd和Kp正定可知,是全局渐近稳定的平衡点,即从任何初始条件出发,总有,因此可实现全局稳定的轨迹跟踪。
最后,将式(30)代入式(24)后得到控制律为:
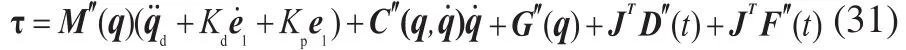
将广义驱动力转换为各关节驱动力F2为:

3.3 多模型控制策略
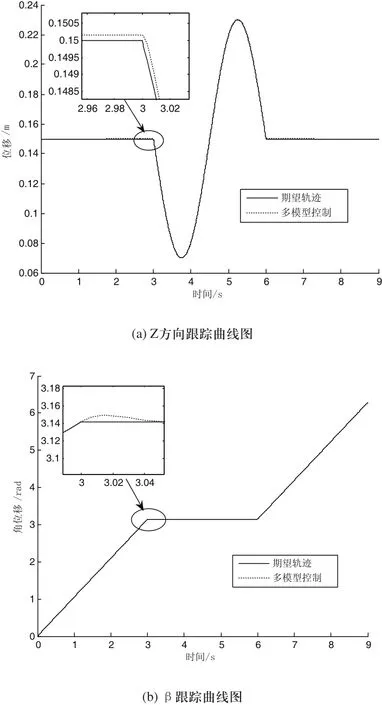
为满足汽车电泳涂装工艺要求并切合工程应用,本文设计了依据时间切换的多模型控制策略:当0≤t 图5 多模型控制流程图 为验证针对升降翻转机构所设计的动力学多模型控制策略的正确性和有效性,本文进行了MATLAB仿真。仿真模拟了汽车电泳涂装输送的完整工艺流程:车身在入槽前水平放置,在行走机构驱动下行进至槽体后,由升降翻转机构驱动车身逆时针翻转180°使车顶向下浸入槽液,之后,升降翻转机构和底盘小车配合,升降翻转机构作上下运动,底盘小车匀速向前,两种运动合成轨迹为正弦波浪式轨迹,电泳涂装过程结束后,由升降翻转机构驱动车身逆时针翻转180°,车身出槽。 期望运动轨迹qd如式(33)、式(34)所示,涂装输送运动时间为9s: 根据机构设计,升降翻转机构物理参数为:mp=17kg,ml1=3.5kg,ml2=1.5kg,ml3=3kg,ml4=0.5kg,m1=m2=2kg,ma=0.5kg,mb=0.25kg,a=0.65m,b=0.56m,c=1.125m,rl3=0.015m,r1=0.05m,r2=0.03m,L1=0.311m,L4=0.65m,θ=120°。根据工艺流程对升降翻转机构的运动要求以及所设计滑模控制器的特点,并根据文献[11,12]可知,确定升降子系统与翻转子系统的粘性系数矩阵Bc为diag(0.7,0.7,0.7,0.7,0.9,0.9),库仑摩擦力矩阵Fc为diag(3.5,3.5,3.5,3.5,4.1,4.1),外界干扰。仿真时,设置连接杆中心点的初始位姿为[0.15m, 0,0, 0]。通过仿真调试,选取滑模控制器参数分别为:a1=80,a2=20,K1=800,K2=100。计算力矩控制器参数分别为:Kd=[9980 0; 0 15110],Kp=[9050 0; 0 100100]。混联机构在所设计多模型控制器作用下的轨迹跟踪曲线如图6所示,其中图6(a)为连接杆中点位姿在z方向的跟踪曲线,图6(b)为连接杆中点位姿分量β的跟踪曲线,图7给出了在多模型控制器作用下混联机构连接杆中点位姿分量的轨迹跟踪误差曲线。 图6 连接杆中点位姿各分量的轨迹跟踪曲线 图7 连接杆中点位姿各方量的轨迹跟踪误差曲线 利用MATLAB中的“tic”、“toc”指令测试所建立动力学模型计算时间结果为,整体动力学模型计算用时0.103s,多模型控制时所建立翻转子系统动力学模型计算用时为0.082s,升降子系统动力学模型计算用时为0.096s。测试结果表明,采用多模型控制策略,有效缩短了计算时间,因此能有效提高控制系统的实时性。由图6可以看出,混联机构连接杆中心点位姿的跟踪轨迹在所设计动力学多模型控制器作用下具有较好的动态和稳态性能。由图7可见,在多模型控制器作用下,混联机构连接杆中心点位姿在z方向的最大绝对误差为2.067×10-3m,β的最大绝对误差为7.413×10-3rad。综合图6和图7可见,在所设计动力学多模型控制器作用下,混联机构具有良好的运动控制性能。 针对一种新型混联式汽车电泳涂装输送机构,为解决具有复杂动力学模型的控制系统难以实现动力学实时控制的问题,并针对该输送机构具有多模式运动的特点,提出一种多模型控制策略。 本文的主要贡献有: 1)建立混联机构动力学模型,然后将完整动力学模型简化为翻转系统和升降系统两个子系统模型。 2)提出一种多模型控制策略,并基于MATLAB/Simulink仿真平台进行测试和仿真试验。对完整动力学模型和两个子系统动力学模型的测试结果表明,采用多模型控制策略可有效提高控制系统的实时性;对多模型控制系统的仿真结果表明,在所设计动力学多模型控制器作用下,混联机构具有良好的运动控制性能。 论文下一步的工作是通过上位机和UMAC运动控制器的软件编程完成汽车电泳涂装输送混联机构的多模型控制试验研究。 [1] 刘辛军,陈祥,高国琴.一种三自由度汽车涂装输送机[P].北京:CN102817064A, 2012-12-12. [2] Qiang Zeng, Yuefa Fang.Structural synthesis and analysis of serial-parallel hybrid mechanism with spatial multi-loop kinematic chains[J].Mechanism and Machine Theory.2012,49:198-215. [3] 郭希娟,黄天宇,常福清.动态式连接的少自由度混联机构的运动学分析[J].机械工程学报.2013,49(1):1-7. [4] Aghili, F.A uni fi ed approach for inverse and direct dynamics of constrained multibody systems based on linear projection operator:applications to control and simulation[J].IEEE Trans. Robot.2005,21(5):834-849. [5] M. Honegger, A. Codourey,E.Burdet, Adaptive control of the Hexaglide,a 6-DOF parallel manipulator[A].Proceedings of the 1997 IEEE International Conference on Robotics and Automation[C].Albuquerque,NM,USA,1997,543-548. [6] 郝齐.一种两自由度并联机构优化设计及动力学控制研究[D].清华大学,2011. [7] 王锡春,李文刚.极电泳涂装工艺设备的精益优化[J].现代涂装.2012,15(3):35-39. [8] 冯德进,薛涛,钱东.浅谈汽车电泳涂装[J].现代涂装.2013,16(11):61-63. [9] 王跃灵,金振林,李研彪.球面3-RRR并联机构动力学建模与鲁棒-自适应迭代学习控制[J].机械工程学报,2010,01:68-73. [10] 钟英英,楼云江,徐毅.并联机构动力学建模及控制研究[J].机电工程,2009,26(4):5-8+21. [11] 尚伟伟.平面二自由度并联机器人的控制策略及其性能研究[D].合肥:中国科学技术大学,2008. [12] Alberto Isidori. Nonlinear Control System[M].Berlin: Spring-Verlag,1995. [13] Guoqin Gao,Juan Wen,XinJun Liu.Synchronous Smooth Sliding Mode Control for Parallel Mechanism Based on Coupling Analysis[J].International Journal of Advanced Robotic Systems,2013,10.1-10. [14] 谢宗武,孙奎,黄剑斌.基于模糊自整定PD控制器的机器人计算力矩控制[J].机械设计与制造,2009,6:178-180. [15] 吴军,李铁民,关立文.飞行模拟器运动平台的计算力矩控制[J].清华大学学报,2006,8:1405-1408.
4 仿真结果及分析



5 结论

