基于模型匹配原则的线性系统控制器设计

叶 倩

（无锡职业技术学院，江苏 214121）

0 引言

控制系统中不可避免地存在误差或不确定性，一方面由于被控对象难以用精确的数学模型进行描述而导致的模型误差或不确定性，另一方面由于控制过程的进行，被控对象本身的特性发生变化而导致的不确定性。经典控制理论虽然在一定程度上能处理相关单变量控制系统的不确定性问题，但存在明显的凑试性，且仅限于系统存在微小摄动的不确定性情况；状态空间方法能较好地解决多变量控制系统的分析和综合问题[1]，设计状态反馈控制器可获得较好的稳定裕度，但对于摄动的鲁棒性不够理想[2]。Zames于1981年首次提出了利用控制系统内某些信号间的传递函数的H∞范数作为优化指标的设计思想[3]。本世纪初，美国弗吉尼亚大学Iwasaki等[4,5]将H∞控制问题归结为求解线性矩阵不等式问题，提出了广义Kalman-Yakubovic-Popov（KYP）引理，从而将H∞控制问题转化为一个凸优化问题来处理。文献[6]提出了窗口H∞范数概念，给出了低频段PID控制器设计方法。

本文将从中频段角度考虑连续线性系统的新型PID控制器设计问题，利用广义KYP引理将频域进行分段，并基于模型匹配原则将PID控制器设计转化为求相应区域内H∞范数构成的不等式最优解问题，进一步地将问题转化为求解与系统状态空间参数相关的线性矩阵不等式可行解问题，最后给出一个数值例子来验证所提控制设计方法的有效性。

1 预备知识

1.1 近似模型匹配

图1 典型线性控制系统结构图

考虑图1所示控制系统结构。其中，z表示PID控制器；G(s)表示被控对象传递函数。根据模型匹配原则[7]，选择一个参考模型，其开环传递函数记作Gε(s)，则控制器D(s)的设计可通过求解下述不等式得到：

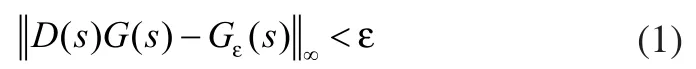
其中，ε是一给定的正实数。ε取值越小，模型匹配的效果越好。

1.2 KYP引理

对于矩阵M，其转置及共轭转置分别记作MT和M*。M是Hermitian矩阵, 即满足M=M*。对于矩阵Φ和P，它们的Kronecker乘积记作PΦ⊗。将2×2的Hermitian矩阵集记作ℍ。定义函数:σ×→ℂℝℍ为：

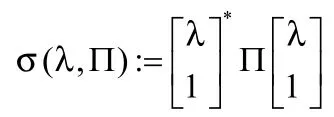
引理1（KYP引理, [5]）给定复矩阵A,B, Π= Π*和(Φ, Ψ)∈Ω，其中：

设(A,B)是能控的，并且A不含特征值λ使得σ( λ, Φ ) = 0 成立。那么以下陈述等价：

1）对于A的所有特征值λ∈Λ，下述不等式成立：

2）存在Hermitian矩阵P和Q，满足Q>0，且：

由引理1可知，通过选择合适的矩阵Φ和Ψ，Λ可表示频域范围内的某一特定区段。对于连续控制系统，可取，则，其中F是实数域的子集，其具体表示的频域范围可由Ψ的选取唯一确定。

2 控制器设计

下面将给出本文在不同频段控制器设计的主要结果。

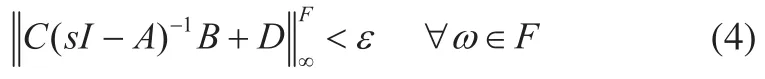
2）存在实对称矩阵P和Q，满足Q>0，使得：

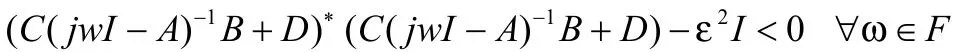
利用实矩阵M满足M*=MT的事实，将上式展开得：

其对应矩阵形式为：

令：

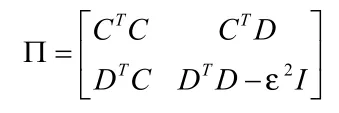
则根据引理1可得, 其成立的充要条件是存在P和Q，满足Q>0，使得：

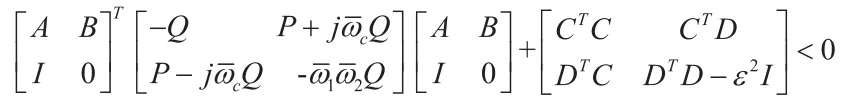
成立。 证毕。

定理1的对偶形式由如下推论给出。

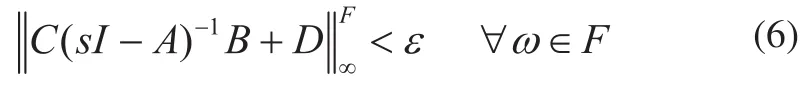
2）存在实对称矩阵P和Q，满足Q0＞，使得：

注意到定理1中矩阵不等式在仿真和实际应用中不方便求解，下面给出简便求解线性矩阵不等式的结果。

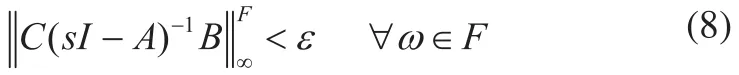
2）存在实对称矩阵P和Q，满足Q＞0，使得：

整理得：

将上面不等式左边第一项进一步矩阵相乘合并得：

3 数值仿真

我们需要设计PID控制器D(s)使得系统在单位阶跃输入下输出响应的中频段没有静态误差。控制器的传递函数和状态空间表达式的各项系数为：

根据传递函数与状态空间表达式之间的转换关系可得：

相应地，匹配模型的开环传递函数可表示为：

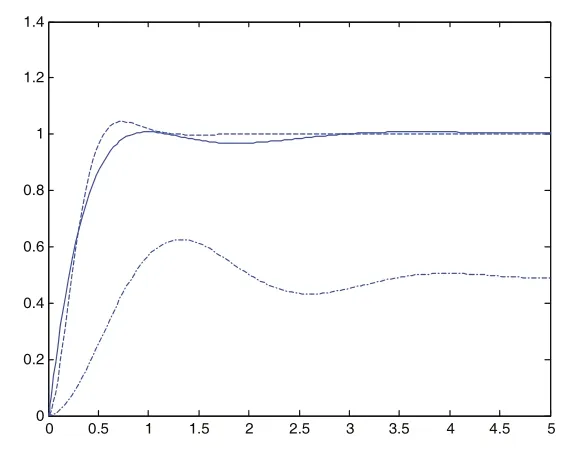
图2 阶跃响应曲线

图3 伯德图

4 结束语

本文提出了基于模型匹配原则的PID控制器新方法，文献[6]给出了低频段的设计方法，本文针对线性控制系统的中频段提出了普适性的定理和推论，应用这些定理及推论便可将PID控制器的优化设计转化为与系统状态空间参数相关的线性矩阵不等式可行解的求解问题，数值仿真例子验证了所设计方法在保证系统鲁棒稳定的情况下，能提高相应频段的性能，满足设计要求。

[1] 王娟,张秀华.基于LMI的一类不确定奇异系统的鲁棒控制[J].控制工程,2013,20(4):691-693+698.

[2] 褚健,俞立,苏宏业.鲁棒控制理论及应用[M].杭州:浙江大学出版社,2000.

[3] Zames G.Feedback and optimal sensitivity: model reference transformations, multiplicative seminorms and approximation inverses[J].IEEE Trans. Automatic Control,1981,26(2):301-320.

[4] Iwasaki T, Hara S.Generalized KYP lemma: unified frequency domain inequalities with design applications[J].IEEE Trans.Automatic Control,2005,50(1):41-59.

[5] Iwasaki T,Hara S.Generalization of Kalman-Yakubovic-Popov lemma for restricted frequency inequalities[C].Proc.of American Control Conference 2003,Denver,Colorado,June 4-6,2003,pp. 3828-3833.

[6] Ma G L, Chen Q, Hu W.Optimal design of PID controller based on window H∞ norm[J].Acta Automatica Sinica,2007,33(9):1000-1003.

[7] Dehghani A,Lanzon A, Anderson B D O. A two-degree-of-freedom H-in fi nity control design method for robust model matching[C].Int J of Robust and Nonlinear Control,2006,16(10):467-483.