提升系统起动过程振动的限制机理研究
李保元,赵 清,魏德印,马凤晨,曹 毅
(1. 河南科技大学 工程训练中心,洛阳 471003;2.河南科技大学 土木工程学院,洛阳 471003)
0 引言
提升系统不仅可以运输煤炭,还可以承载工人和设备上下煤矿,已在现代化矿井不可缺少的重要环节。其动力是通过钢丝绳来实现的,由于钢丝绳是粘弹性体,其具有弹性特性,在提升系统的起动过程中,钢丝绳会产生较大的弹性振动,导致钢丝绳内会形成很大的动张力,常常造成钢丝绳局部张力过大或过小,导致安全事故的发生[1~3]。因此,对提升系统起动过程中弹性振动机理的研究和振动限制是避免起动安全事故发生的关键。
本文通过建立并分析提升系统的弹性振动方程,推导出提升系统在不同激励加速度下的加速度响应方程,在对各加速度响应方程进行弹性振动特性研究后发现,提升系统起动时间T与钢丝绳的固有振动频率mω是决定提升系统起动过程钢丝绳弹性振动大小的两个关键参数。从避免共振的角度出发,提出了提升系统振动的限制机理。并用MATLAB软件对实例进行仿真计算,以验证提升系统起动过程弹性振动限制机理的正确性。
1 提升系统弹性振动方程
不同断面的钢丝绳在同一时间具有不同的速度和加速度,其运动学参数不仅是时间t的函数,也是所研究钢丝绳断面位置x的函数,即 ),( txuu= ,u表示钢丝绳断面x相对于均衡位置的变形[4],如图1所示。钢丝绳位置的坐标原点选在钢丝绳和滚筒的接触处,提升系统的振动偏微分方程为[5]:
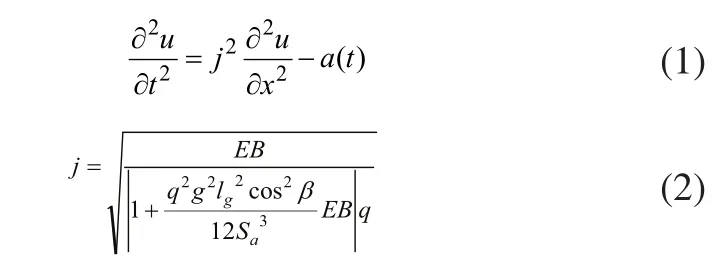
其中:a(t)为激励加速度;j为弹性波传播速度;E为弹性模量;B为钢丝绳直径;q为单位长度质量;β为倾角;S为平均张力。
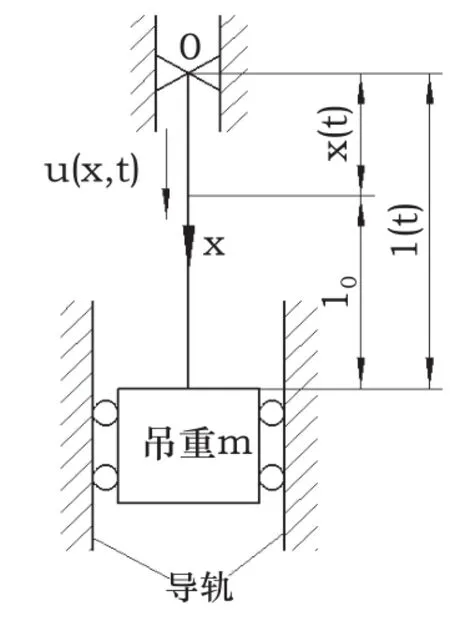
图1 提升系统工作简图
2 提升系统起动加速度响应特性
采用Duhamet原理对以上提升系统的振动偏微分方程进行求解。

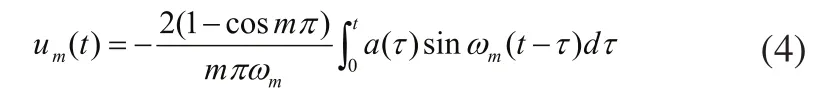
其加速度响应方程的通解为:
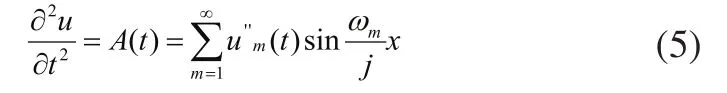
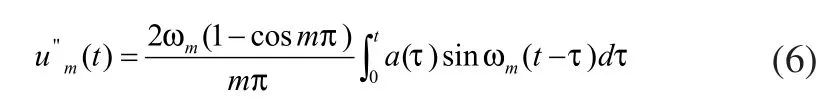
目前,提升系统在起动过程中开始采用S形曲线,其对应的起动激励加速度曲线有多种,我国常用的是抛物线形加速度控制曲线[6],激励加速度曲线计算公式为:
抛物线形加速度曲线:

代入式(4)可求出抛物线形加速度响应计算式为:

可以看出,提升系统起动时间T与钢丝绳的固有振动频率mω是影响加速度响应大小的两个关键参数。本文考虑从这两个参数入手进一步寻求可以限制提升系统起动过程中加速度响应弹性振动的方法。
3 弹性振动限制机理的研究
提升系统运行过程中钢丝绳存在着变化的固有振动频率,且钢丝绳的固有振动频率有无穷多个,且随着提升系统张紧装置的不同而变化。钢丝绳固有振动频率对应的固有振动周期为Tm,当提升系统起动时激励加速度的频率与钢丝绳的某阶固有振动频率相接近时,会产生共振,钢丝绳的弹性振动会加强,即提升系统加速度响应的弹性振动幅度增大。因此,为了限制提升系统系统起动过程中钢丝绳的弹性振动,起动的激励频率应远离提升系统的固有振动频率,即起动时间T应远离提升系统的固有振动周期Tm。
通过上述分析,我们提出了提升系统起动过程弹性振动限制机理:提升系统起动时间T与钢丝绳基波振动周期T1的比值N=T/T1≥X(某个数值)时,可以避免共振现象的发生,提升系统起动加速度响应的振动幅度都能降低激励加速度,在提升系统整个起动过程中,提升系统系统的弹性振动可以被有效地限制和消除。
4 仿真计算
为了验证本文提出的提升系统起动过程弹性振动限制机理的正确性,我们对提升系统抛物线形加速度控制作为激励加速度时,输送机在基波振动周期T1确定的情况下(取1ω=1.000),选择不同的提升系统起动时间T,对不同加速度响应曲线进行MATLAB仿真,得到了不同的加速度响应曲线图。图2为N(T/T1)为10时的抛物线加速度响应曲线图,其中波浪线为加速度响应的波动变化;表1汇总了抛物线加速度响应与N的关系。

图2 抛物线加速度响应曲线图

表1 抛物线加速度响应随N的变化值
其中:Amax为抛物线加速度响应A(t)的最大值。
由图2和表1可以看出,随N的增加,输送机起动抛物线加速度响应的最大值明显减小,曲线振动幅度明显减小。当N≥15时,加速度响应的振动幅度开始降低到激励加速度的4.1%以下,加速度响应曲线较平滑。因此,该仿真结果表明:当抛物线加速度控制曲线的起动时间T与基波振动周期T1的比值N=T/T1≥X(X=15)时,加速度响应的振动幅度降低到激励加速度的4.1%以下,加速度响应的弹性振动被很好的限制。仿真结果完全符合提升系统起动过程弹性振动限制机理。
5 结论
2)仿真计算结果验证本文提出的提升系统起动弹性振动限制机理是正确的,即提升系统起动时间T与钢丝绳基波振动周期T1的比值N=T/T1≥X(某个数值)时,可以避免共振现象的发生,提升系统起动加速度响应的振动幅度都能降低到激励加速度的4.1%以下,在提升系统起动过程中,提升系统系统的弹性振动可以被有效地限制和消除。
[1] 张媛,包继华,于岩,周满山.提升系统动态分析连续模型[J].山东矿业学院学报,1999,18(1):35-39.
[2] 宋玉德.矿井提升机的数字化技术改造[J].煤炭技术,2006,09:28-29.
[3] 张晓林,沈强峻.多绳摩擦提升钢丝绳纵向张力动态特性[J].煤矿机械,2013,12:49-51.
[4] 李玉瑾.提升系统的动态特性分析与起动设计[J].煤炭学报,2002,27(3):294-298.
[5] 刘英林,王彦凤.钢丝绳应力波传播速度[J].太原理工大学学报,1999,30(4):407-409.
[6] Lin C.T.A Neuro-Fuzzy Synergism to Intelligent Systems[J].Neural Networks and Fuzzy S.ystems,1996,16(8):56-58.

