浅谈PMSM无速度传感器速度估算

张 虎，孙安博，樊生文

（北方工业大学 电力电子与电气传动北京市工程中心，北京 100144）

0 引言

永磁同步电机（PMSM）是随着现代电力电子技术的迅速发展而逐渐兴起的一种新型电机。PMSM具有具有优越的调速性能，主要体现在控制性能好、调速范围宽、运行平稳、效率高等方面[1]。

永磁同步电机的定子是由对称绕组构成，转子则是2至8对永磁体按照N极和S极交替排列在转子周围构成的。永磁同步电机的定子和转子与传统直流电机类似，只是定子变为了转子，转子变为了定子，相比于直流电机，最明显的区别在于永磁同步电机没有换向器和电刷，取而代之的是位置传感器。这样，永磁同步电机的结构得以简化的同时又降低了电机制造和维护的成本，但是对电机控制器的要求提高了[2]。

在对永磁同步电机的控制过程中，需要实时监测电机的转速，而待测的转速可通过与电机同轴的速度传感器监测并计算出来。但是，有速度传感器的PMSM控制系统也有诸多弊端，增加了生产的成本；对传感器的安装位置要求极高，安装不当则会影响监测精度；增加了电机的转动惯量，对电机的损耗性增加，也增加了维护的成本等等。基于以上种种问题，迫使人们开始重视PMSM无速度传感器控制的研究，成为近年来的热点[3～5]。

无速度传感器的控制技术是指在不安装速度传感器的前提下，结合永磁同步电机的数学模型，人工整定出一套算法，估算转子的转速。无速度传感器的控制技术优势十分明显，降低了系统的制造和维护成本也避免了由传感器引起的转动惯量增大等弊端，以后必将广泛应用与生产生活中[6]。

早在1955年，以美国D.Harrison为首的科研团队就已经提出了用晶体管换相电路代替机械电刷的理论，并为此申请了专利，为以后PMSM的发展奠定了基础。而PMSM无速度传感器的研究始于20世纪70年代，多年来国内外学者的研究取得了显著的成果。美国的R.D.Lorenz教授于1993年提出了高频注入的方法，发表了多篇学术论文，并获得了多项专利。韩国的Seung-Ki Sul教授在无速度传感器的控制技术方面也颇有建树。此外，德国的Joachim Holtz教授和澳大利亚的M.F.Rachman教授等等都在从事着相关的研究，为PMSM无速度传感器控制技术的发展做出突出贡献[7]。

1 PMSM无速度传感器速度估算的几种方法

随着无速度传感器控制技术的逐步成熟，涌现出越来越多优秀的速度估算方法，本文将其简单分为线性系统算法和非线性系统算法两大类，方便对比研究。下面就这几种常用算法做简单的介绍。

1.1 线性系统算法

1.1.1 基于电压方程的直接计算法

当永磁同步电机的转子在旋转的过程中，永磁励磁磁场会产生反电动势，建立永磁同步电机的数学模型后，在反电动势的公式中包含转子位置角的信息，可依此估算出转子位置角，进而可求出转子转速。

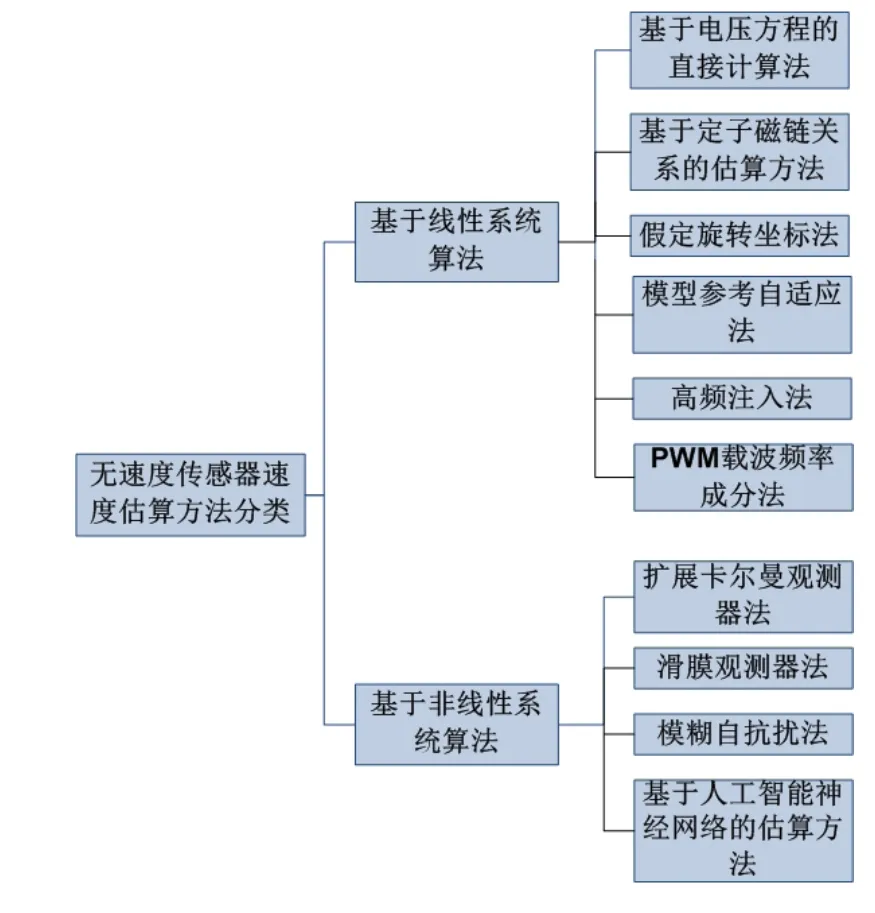
图1 无速度传感器速度估算方法分类示意图

永磁同步电机数学模型：

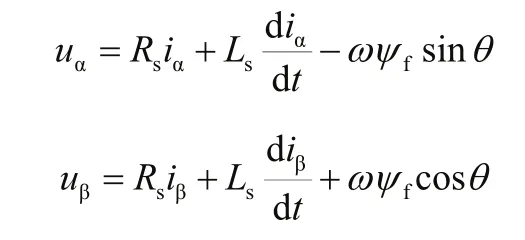
而反电动势：

据此可得：

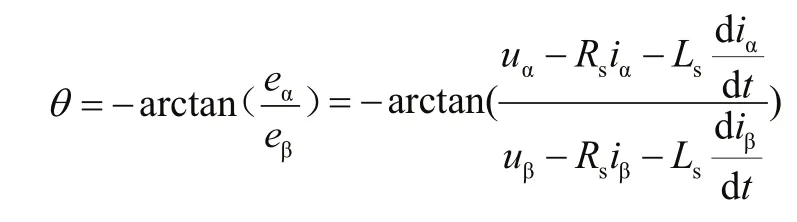
进而可得：

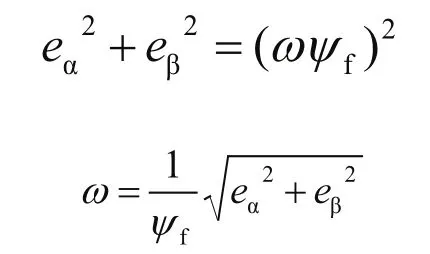
此算法的优点是所有变量都可直接测量得到，计算简单，且动态性能好，但是很依赖电机参数，属于开环计算，不能根据扰动的影响自行调整，所以抗干扰性较差。而在实际情况中，环境会对电机参数产生一些影响，这会使转速的估算产生偏差。应用此方法时，一般会结合电机参数在线辨识，会使准确性大大上升。此外，由于式中包含微分项，也会对计算准确性造成影响[8～10]。

1.1.2 基于定子磁链关系的估算方法

永磁同步电机转子旋转速度与磁链旋转速度同步，所以可以通过磁链旋转角度信息推算出转子旋转速度。

永磁同步电机旋转坐标系下电压方程为（忽略反电动势）：

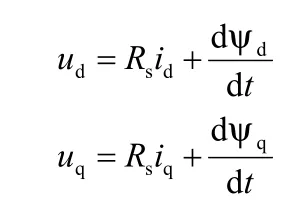
进而可得到定子磁链方程：

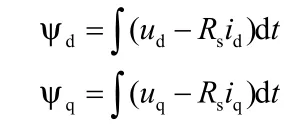
定子磁链旋转角度为：

这种方法的弊端有二：1）由于积分的作用会产生零漂、相移等现象，对转速估算准确性造成一定影响。2）鲁棒性较差，当环境变化时，磁路饱和会造成电机参数变化，也使转速估算的误差变大。种种限制，导致基于定子磁链关系的估算方法只能应用于对电机性能要求不高的场合[11]。

1.1.3 假定旋转坐标法

假定旋转坐标系类似于传统旋转dq坐标系，选择了以xy作为参考坐标系，y轴超前于x轴90电角度，所不同的是dq坐标系中d轴是由永磁励磁磁链方向确定的，而x轴是由估算的励磁磁链方向确定的（即估算的转子位置）。

其中，将θΔ定义为x轴与q轴的夹角，这样假定旋转坐标系可以通过控制Ux、Uy来控制旋转电流矢量is。

图2 假定旋转坐标系

假定旋转坐标法的最终目的是使假设转子位置与实际转子转子位置一致，以达到准确的转速估算。具体的实施方法为对θΔ或者可以反映θΔ信息的物理量进行PI运算，进而得到转速的修正值[12]。

假定旋转坐标法能够准确的估算出转子转速，算法相对简单易于实现，但仍然不能摆脱对电机参数变化的影响。而当θΔ处于某些角度时，电角度的误差不会收敛至零，会使转速的估算值一直处于震荡状态，对系统造成极大影响。

1.1.4 模型参考自适应法

模型参考自适应法是目前一种比较常用的转速估算技术，由C.Schauder于1989年首次应用到电机转速辨识当中。模型参考自适应系统的特点是采用参考模型规定系统所要求的性能，其结构如图3所示[13]。

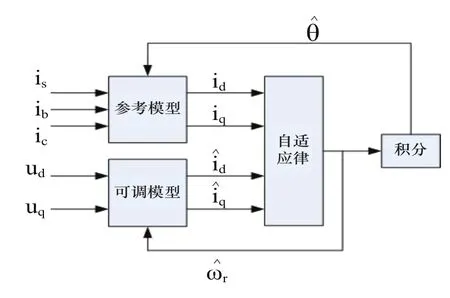
图3 模型参考自适应简图

外部输入同时激励参考和可调模型，两模型的输出具有相同的物理意义。参考模型输出量规定了一个给定的性能指标，这个性能指标与测得的可调模型输出比较后，利用其差值构造适当的自适应律，由自适应律来修改可调模型的参数，使可调模型的输出可以快速且稳定的跟踪参考模型的输出，即使差值逐步趋近于零[14,15]。

根据参考模型与可调模型选取的不同，可以构造不同的自适应系统。

其中一种方案是，采用以定子磁链矢量为参考模型的自适应系统，基于电压和电流方程计算出定子磁链，并以此为可调参数，之后通过自适应律可估算出转子转速。

而最常用的方法是基于定子电流模型的自适应系统，依据Popov超稳定性理论可得到此转速估算系统的自适应律[17～19]，从而可得到电机的转速。

模型参考自适应系统是一种闭环计算方法，相比于开环计算方法有了很大的改进，计算精度和抗干扰性得到了提升，然而由于参考模型一般都是选取电机稳态模型，导致在电机转速较低时，转速估算精度较低，具有一定局限性。

1.1.5 高频注入法

诸多方法都是适合于电机高转速时的速度估算，对于低速时的转速估算误差较大。为解决这一问题，美国的M.L.Corley教授和R.D.Lorenz教授于1993年首次提出了高频注入法来进行电机低速情况下的转速估算。

高频注入法的主要思想是将高频电压或者电流信号注入电机定子绕组，利用电机结构的不对称性检测对高频电压或电流注入所产生的响应信号，再通过信号处理能够获取转子位置信息进而可估算出转子转速[20]。

根据不同的高频注入信号，可将高频注入分为三种方法。

旋转高频电压注入法：旋转高频电压注入法是较为常用的一种方法，信号的注入较为容易实现，但其缺点是提取高频信号时需要较多的滤波器，无疑增加了信号处理的难度。其原理是在基波励磁上叠加一个三相平衡的高频电压信号，而后可在反馈中检测到高频信号响应，如下所示：

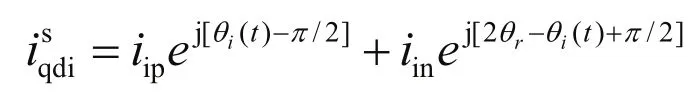
式中包含转子位置信息，可由此推算出转子转速。

图4 旋转高频电压注入法简图

旋转高频电流注入法：旋转高频电流注入法相比于电压注入法的优点在于高频信号响应的幅值大，但为了获得更好的效果需要对电流调节器进行改造。其原理是在基波励磁电流上叠加一个三相平衡的高频电流信号，在PWM逆变器输入端能够检测到高频电压响应，由此可推算出转子转速。

高频脉振电压注入法：高频脉振电压注入法类似于高频电压注入法，区别在于脉振电压注入法在d轴注入高频正弦电压信号。其优点在于产生电磁转矩脉动小而且应用场合广，不仅仅适用于凸极式永磁同步电机，还可以应用与隐极式永磁同步电机[21]。

由于高频注入法是采用外加高频激励信号来追踪凸极，与电机参数和转速无关，所以不仅鲁棒性好，而且能够在电机低速甚至零速的情况下较为准确的估算出转子位置和转子转速。高频注入法的缺点在于注入高频信号会产生转矩脉动，影响电机性能，而且滤波器的使用也会对动态响应产生影响。此外，高频注入法对电机的结构有一定要求，也限制了这种方法的应用场合[22]。

1.1.6 PWM载波频率成分法

高频注入法需要向电机中注入高频信号，注入的高频信号会引起转矩脉动，影响电机的动态性能。PWM载波频率成分法也是利用了电机的凸极性，相比于高频注入法拥有有一个显著优势：无需额外的注入信号。PWM载波频率成分法的主要思想是利用PWM电压型逆变器输出的固有谐波电压和相应的电流响应，结合最小二乘法获得反电动势参数，据此可推算出转子转速[23]。

PWM载波频率成分法具有很好的性能，在低速甚至零速时也能保证转速估算的精确性，而且不需要进行坐标变换，但是却需要大量的代数运算。此外由于PWM的电流响应变化很小，需要精度很高的电流传感器才能对信号进行处理[24]。

1.2 非线性算法

1.2.1 扩展卡尔曼观测器法

R.E.Kalman于1960年发表的论文阐述了一种离散线性数据滤波问题的递推方法，此后逐步完善成为卡尔曼滤波器的理论基础。如今，基于扩展卡尔曼观测器技术的无速度传感器矢量控制系统已广泛应用与电机控制之

中[25]。

扩展卡尔曼滤波器是卡尔曼滤波器在非线性系统中的推广，提供了一种迭代形式的非线性算法。卡尔曼滤波器由一个状态方程和一个观测方程构成，确定了初始状态后，依据状态方程可递推出下一个状态的初步预测，而后通过测量值和观测值的误差对状态量进行校正，根据误差协方差最小原则可以确定校正系数。若定义xk为状态矢量，，yk为观测矢量，，以上可用公式进行描述。

时间更新方程：

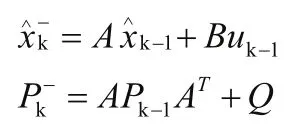
测量更新方程：

卡尔曼滤波器可分为时间更新方程和测量更新方程，时间更新方程通过当前时刻的状态估计和估计协方差估计更新下一步的初步估计值，测量更新方程通过反馈将初步估计换算到最终估计[26]。

扩展卡尔曼滤波器能够削弱随机干扰，还可以很好的预测噪音的影响，拥有较强的抗干扰性，因而对变量的估算比较准确。但是算法复杂，计算量庞大，对运算器的要求较高。同时对电机参数也有依赖性，配合电机参数在线辨识可获得更好的估算效果。

1.2.2 滑膜观测器法

滑膜观测器是基于滑模变结构理论构造的观测器。滑模控制本质上是一种特殊的非线性控制，这种控制策略特殊之处在于系统的结构可以处于动态过程中，根据当前系统状态变化而变化，这就呈现为系统按照滑动模态的状态轨迹运动[27]。

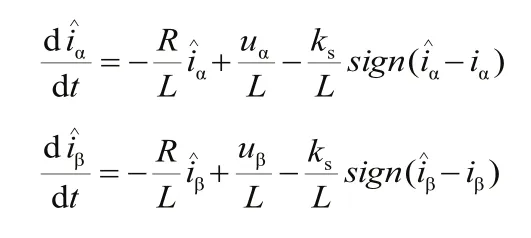
其中sign(x)为符号函数，ks为滑模增益。将以上方程两两相减可得：

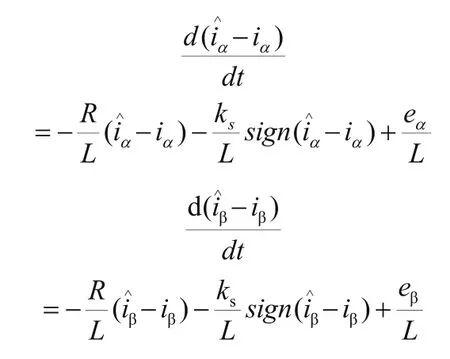
一阶滤波器会引起系统中的相位的延迟，此时需对角度进行补偿，补偿值可通过以下算式求得：

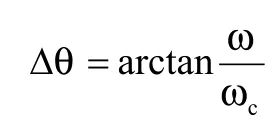
最终估计值为：

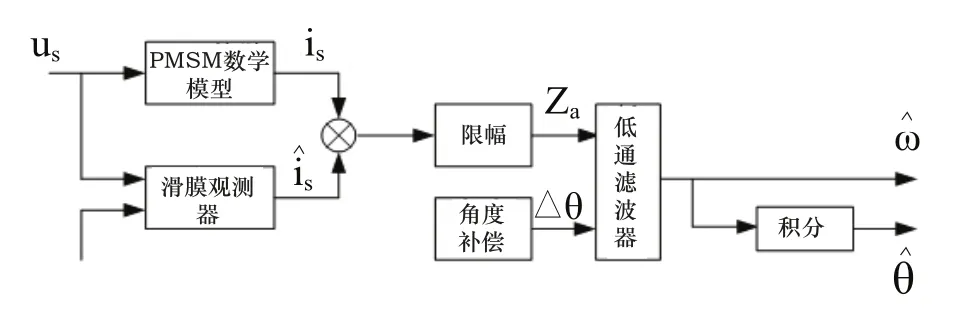
图5 滑膜观测器简图

反电动势式中含有转子位置信息，由此可得转子转速估算。滑模面方程的选择以及滑模增益的选取决定了滑模观测器的动态性能，既要保证滑模算法的收敛性以及收敛速度，也要保证由于滑模增益过大引起的电机转矩脉动。

滑模观测器的优点在于算法相对简单，易于实现，而且观测值具有良好的鲁棒性，这是由于滑膜观测器受电机参数变化以及外部扰动影响小。但是，由于滑模观测器是非连续性系统，导致系统会出现“抖振”的现象，而“抖振”现象只可抑制不可消除，这对滑模观测器的应用场合造成了一些限制。

1.2.3 模糊自抗扰法

由于诸多转速估算算法对电机参数有依赖性，导致抗扰能力受到影响。为提高系统的鲁棒性和自适应能力，有学者提出了自抗扰的永磁同步电机控制方法。在实际应用当中，针对于自抗扰控制器参数不便于整定以及实际操作的问题，引入了模糊控制的思想，总结出了一种基于模糊控制原理的改进型自抗扰控制算法，这就是模糊自抗扰法的雏形。

模糊自抗扰法的主要思想是：通过对永磁同步电机数学模型的分析，推导出模糊自抗扰转速环调节器，以转速和交轴电流对直轴电流环的耦合作用作为直轴电流环的扰动量，利用扩张状态观测器将其观测出来，进而估计出电机实际转速，以实现无速度传感器控制。

模糊自抗扰法是一种改进的非线性PID控制技术，它的优势在于不依赖电机的数学模型，将系统的内部扰动和外部扰动作用均当作对系统的扰动而自动估计并给予补偿，可以实现卓越的控制性能，并且算法相对简单，数字化易于实现。在不同的转速下，模糊自抗扰法表现出很强的自适应能力以及对系统扰动优越的鲁棒性，并且具有高精度的转速估计。经过大量实验可以证明，模糊自抗扰法在永磁同步电机无速度传感器技术领域的可行性以及优越性[28]。

1.2.4 基于人工智能神经网络的估算方法

人工智能神经网络是一种模仿生物神经网络行为特征，能够进行分布式并行信息处理，具有自组织、自学习、自适应以及很强的非线性函数逼近能力的新式算法。这种算法系统复杂，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的[29]。

智能控制技术的高速发展，使人工智能神经网络在工学方面的研究日趋深入，在无速度传感器技术方面也颇有成果。基本思想是构造神经网络模拟电机模型，对观测数据和实测数据之间的误差进行在线调节，使观测数据无线接近实际数据。

基于人工智能神经网络的转速估算技术具有优越的性能。首先，它完全依靠实际估算效果进行控制，不依赖控制对象的数学模型，在控制过程中可充分考虑系统的不确定性和误差进行优化调整。其次，它具有明显的非线性特征，在理论上具有任意逼近非线性有理函数的能力。然而，基于人工智能神经网络的转速估算技术尚处于研究阶段，其理论基础还在逐步完善，在生产生活中大规模应用还有距离，但可以预见的是这种方法具有广阔的前景[30～33]。

3 结束语

本文介绍了十种常用的PMSM转子转速估算方法，按照各自属性将算法分为线性系统算法和非线性系统算法，对每种方法的原理做了简要介绍，并指出个中优劣，为了解PMSM无速度传感器技术提供帮助。

[1] Md Enamul Haque,Limin Zhong,Muhammed Fazlur Rahman.A Sensorless Initial Rotor Position Estimation Scheme for a Direct Torque Controlled Interior Permanent Magnet Synchronous Motor Drive[J].IEEE Transactions on Power Electronics.2003,18(6):1376-1383.

[2] Fitzgerald A E,Kingsley C K,Umans S D.Electric Machinery[M].Fourth Ed.New York:McGraw-Hill,1983.

[3] L.A.Jone,J.H.Lang.A State Observer for the Permanentmagnet Synchronous Motor[J].IEEE Transactions on Industrial Electronics.1989,36(3):374-382.

[4] 李永东,朱昊.永磁同步电机无速度传感器控制综述[J].电气传动.2009.39(9):3-10.

[5] 潘萍,付子义,刘辉,曾咪.永磁同步电机无传感器控制技术研究现状与控制策略综述[J].工矿自动化,2007,29-31.

[6] 苏健勇,李铁才.PMSM中高低速段无位置传感器控制方法综述[J].技术纵横.2014.2(1):31-34.

[7] 戴永亮,孙力,张晓光,赵克.永磁同步电机无传感器控制技术综述[J].伺服控制.2011.4:23-33.

[8] 张虎.无速度传感器矢量控制和参数辨识技术研究[D].北京科技大学,2010:48-95.

[9] 谷善茂,何凤有,谭国俊,叶生文.永磁同步电动机无传感器控制技术现状与发展[J].电工技术学报,2009.14-20.

[10] 张文敏,李伟力,沈稼丰.永磁无刷直流电动机反电动势及定位力矩的计算与仿真[J].哈尔滨工业大学学报.2006.38(2):297-300.

[11] 王林翮.永磁同步电机无速度传感器矢量控制系统的研究[D].西南交通大学,2009.36-51.

[12] 纪历,徐龙祥.基于假定旋转坐标的高速永磁同步电机无传感器控制[J].电工技术学报.2012.27(11):55-61.

[13] 王元成,夏加宽,孙宜标.现代电机控制技术[M].机械工业出版社.2012.179-206.

[14] Wu R,Slemon G R.A Permanent Magnet Motor Drive Without a Shaft Sensor[C]//IEEE Industry Applications Society Annual Meeting,1990,1:553-558.

[15] 孟令欣.基于MRAS的永磁同步电机矢量控制系统的研究[D].东北大学,2013.35-43.

[16] Maiti Suman,Chakraborty Chandan. Reactive Power Based Speed Sensorless Controller for Permanent Magnet Synchronous Motor Drive[A].IEEE International Conference on Industrial Technology[C].ICIT,2006,1:247-252.

[17] 钟康.基于MRAS算法的永磁同步电机无速度传感器控制研究[D].华中科技大学,2009.22-45.

[18] 王飞.永磁同步电机无传感器矢量控制方法研究及仿真[D].上海交通大学.2008.29-61.

[19] 朝泽云.无速度传感器矢量控制系统的若干问题研究[D].华中科技大学,2006.59-87.

[20] 陈力.基于高频注入法永磁同步电机无传感器矢量控制的研究[D].天津大学,2009.23-57.

[21] 张仕平.高频注入法PMSM无传感器矢量控制的研究[D].湖南大学,2013.24-44.

[22] 王丽梅,郭庆鼎.基于多重凸极跟踪的永磁同步电动机转子位置估计[J].中国电气工程学报.2007.27(24):48-52.

[23] R.Krishnan,柴凤.永磁无刷电机及其驱动技术[M].机械工业出版社.2014:348-369.

[24] 于艳君.基于载波频率成分法的永磁同步电机无位置传感器控制研究[D].哈尔滨工业大学,2009.15-32.

[25] 李刚.内置式PMSM无位置传感器矢量控制技术研究[D].哈尔滨工业大学,2012:16-33.

[26] 姚卫忠.卡尔曼滤波器在永磁同步电机矢量控制磁同中的应用研究[D].浙江大学,2008.24-53.

[27]刘军.基于滑模观测器的PMSM无位置传感器矢量控制的研究[D].浙江大学,2014.17-28.

[28] 黄庆,黄守道,匡江传,张志刚,李孟秋,罗德荣.基于模糊自抗扰的PMSM无速度传感器控制[J].湖南大学学报,2012.37-43.

[29] 孙海军,郭庆鼎,高松巍,杨理践.系统辨识法永磁同步电机无传感器控制[J].电机与控制学报,2008.244-253.

[30] 王高林,张国强,贵献国,徐殿国.永磁同步电机无位置传感器混合控制策略[J].中国电机工程学报,2012.103-109.

[31] 王耀南,陈维.无速度传感器的感应电机神经网络鲁棒自适应控制[J].中国电机工程学报,2008.92-98.

[32] 杨金磊.基于无传感器的永磁同步电动机矢量控制系统的研究[D].哈尔滨理工大学,2009.15-17.

[33] 王菲菲.永磁同步电机无传感器矢量控制系统设计[D].哈尔滨工业大学,2008.20-25.