部分相干光在斜程和水平大气湍流中的光强与扩展

柯熙政，王婉婷

西安理工大学自动化与信息工程学院，西安710048

部分相干光在斜程和水平大气湍流中的光强与扩展

柯熙政，王婉婷

西安理工大学自动化与信息工程学院，西安710048

基于广义惠更斯-菲涅尔原理、交叉谱密度函数，利用修正von Karmon谱模型以及ITU-R颁布的大气折射率结构模型，首先推导出部分相干高斯-谢尔光束在大气湍流中斜程和水平传输时的光强分布以及光束扩展解析式，然后分别从归一化光强分布和相对束宽的角度讨论并对比了斜程和水平传输时天顶角、湍流强度、光束相干长度等参数对光束光强分布和扩展的影响，并给予相应的物理解释.研究表明：1）部分相干高斯-谢尔光束在自由空间中水平传输时的归一化光强与斜程传输时的光强分布相同；2）天顶角越小，光束的归一化强度分布越集中，峰值光强越强，同时所受湍流的影响也越小.3）在斜程传输情况下，天顶角、湍流强度、光束相干长度等参数对光束扩展的影响与水平传输几乎一致.

部分相干光；斜程传输；归一化强度分布；光束相对束宽

激光在大气中传输的理论和实验研究，对于激光通信、卫星遥感以及激光定位等方面具有重要意义.随着广义惠更斯-菲涅尔原理、Rytov相位结构函数平方近似以及维格纳分布函数等理论的发展，大气湍流中关于光束传输特性的研究也取得了不少进展.文献［1］通过对高斯-谢尔模型部分相干光大气传输理论的研究，发现部分相干光比完全相干光具有更强的抗湍流能力.文献［2］研究了大气湍流中部分相干光的均方束宽，发现部分相干光比完全相干光所受湍流影响更小.文献［3］给出了高斯光束的平均光强和光束短期扩展表达式，并研究了该光束等效半径与传输距离、初始半径与光波波长之间的关系.文献［4］研究了非傍轴多色部分相干拉盖尔高斯光束在自由空间中传输时的强度分布变化情况.文献［5］分析了光束的相干长度、波前曲率半径及波束宽度等参数在优化之后对系统性能的改善情况.由于在实际应用中经常涉及到斜程传输，研究斜程传输时大气湍流对光束光强分布和扩展的影响非常有意义［6］.当光束在大气湍流中传输时，由于大气折射率的随机起伏，光束的波前相位发生畸变，从而产生光束扩展、漂移及光强闪烁等现象.不同的大气湍流尺度对光束传输特性的影响不同，斜程传输和水平传输的主要差别在于大气折射率结构常数的不同.斜程传输路径上的大气结构常数随高度的变化而变化，同时受风速、温度、湿度及气压等因素的影响；水平传输时大气结构常数一般可取典型值，因此对斜程传输时的研究较为复杂.文献［7］以部分相干平顶光束为例，分析了光束在斜程传输时的光束阶数、空间相干度、天顶角等参数对光束束宽的影响.文献［8］研究了GSM光束在大气湍流中以上行、下行、水平3种不同路径传输时的平均强度和均方束宽，并发现在大气湍流中以下行链路传输时光束所受影响最小.然而，对于光束在大气湍流中斜程传输时的光强分布的相关研究还很少见，且对天顶角、湍流强度、相干长度等参数的研究大多局限于对相应参数取特定值的方式，而没有全面反映光束传输时各种参数对传输特性影响的变化情况.因此，本文针对天顶角、湍流强度、相干长度等参数对光束在大气湍流中传输时的影响情况进行全面系统的分析讨论.

本文以部分相干高斯-谢尔（Gaussian-Schell，GSM）光束为模型，利用广义惠更斯-菲涅尔原理、交叉谱密度函数以及束宽的定义式，推导了光束在大气湍流中斜程和水平传输时光强分布及光束扩展表达式，最后分别从归一化强度和相对束宽的角度系统分析了天顶角、湍流强度、光束相干长度等各项参数对光束光强分布和扩展的影响.

1　理论部分

部分相干GSM光束在z=0平面内的交叉谱密度［9］

式中，ρs1、ρs2分别为源平面两点的坐标矢量，参数A、σs、σg分别为光源的光强、束腰宽度、相干长度.

基于广义惠更斯-菲涅尔原理，GSM光束通过大气湍流后z处的交叉谱密度为［10］

式中，ρ1、ρ2分别为z平面两点的坐标矢量，为系综统计平均，其计算公式为

式中，Dφ（ρs1-ρs2，ρ1-ρ2）为波结构函数，斜程传输时可表示为［11］

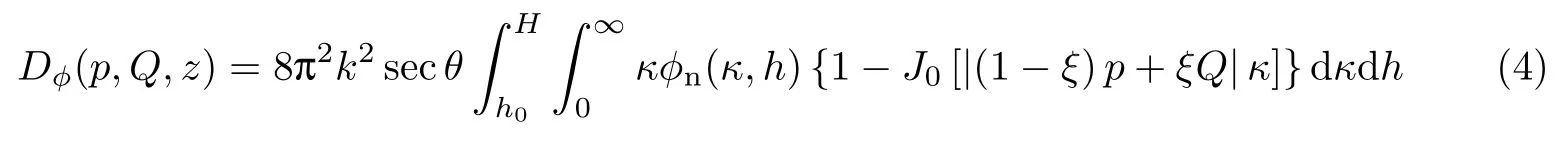
式中，p=ρ1-ρ2，Q=ρs1-ρs2，J0为第1类零阶贝塞尔函数，φn（κ，h）=φn（κ（h），φn（κ）为折射率功率谱，为大气折射率结构模型，两者相互独立.由于光束下行传输所受湍流的影响小于上行传输，本文仅研究上行传输的情况［12］，即，其中H为接收机距离地面的垂直高度，h0为发射机距离地面的垂直高度.

在强湍流条件下，式（4）中的贝塞尔函数可利用前两项来近似［13-14］，有

将式（5）代入式（4），经积分化简后可得

式中

将式（1）和（6）代入式（2），可得

令式（7）中的ρ1=ρ2=ρ，并对该式进行积分求解，即可得到GSM光束斜程传输时的强度分布式

式中

从式（8）～（8c）中可以看出，光束强度与大气折射率结构常数、光束相干长度以及束腰宽度有关.式（8）与文献［3］水平传输条件下所推导出的式（37）相似.对于湍流项M中的湍流功率谱模型［11］，本文采用将内外尺度均考虑在内的修正von Karmon谱，其表达式为

式中，κm=5.92/l0，κ0≈2π/L0，l0和L0分别为湍流的内外尺度；为大气折射率结构模型，这里采用ITU-R在2001年所提出的随高度变化的模型，可以表示为

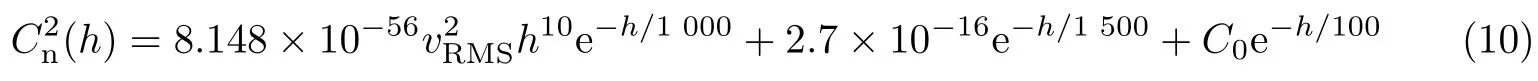
为了分析大气湍流对光束强度分布的影响，定义光束的归一化光强为［14］

式中，Its（ρ，z）为光束在大气湍流中斜程传输时的强度分布，为完全相干光束在自由空间中斜程传输时的轴上光强值.

通过计算可求得该光束的归一化光强

根据光束扩展均方根束宽定义［14］可知

将式（8）代入式（13）可得

该式的前两项表示由自由空间衍射引起的光束扩展量，第3项代表湍流引起的光束扩展量［2］.

为直观地分析湍流对光束扩展影响的大小，定义相对束宽为湍流中束宽与自由空间束宽之比，其表达式为

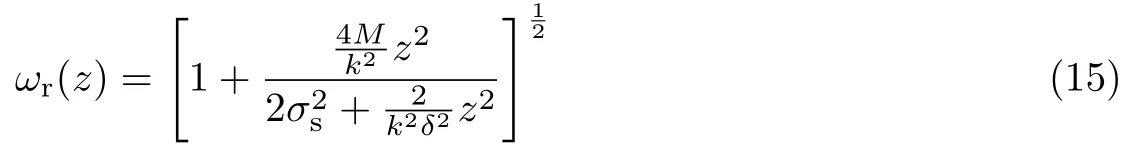
结合式（12）和（15），下面对GSM光束以斜程和水平方式在大气湍流中传输时的光强分布及光束扩展进行系统的分析与讨论.

2　GSM光束在湍流大气中传输的光强分布

完全相干和部分相干GSM光束在大气湍流中传输时的光强归一化分布如图1所示.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3［11］，近地面风速vg=2.8 m/s；水平传输时，大气折射率结构常数（2）=1.7×10-14m-2/3［11］，传输距离z=7 071 m.根据H=zcosθ+h0可知斜程传输时的高度约为5 000 m，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m，波长λ=650 nm.在图1中，和分别为光束在自由空间和湍流大气中水平传输时的归一化光强.由图1可以看出，无论是完全相干还是部分相干GSM光，在自由空间中以斜程传输和水平传输两种方式传输时的强度分布均相同，即光束在自由空间中传输时的强度分布与传输方式无关，这可从式（8）得到解释.当光束在大气湍流中传输时，湍流项M的表达式在斜程和水平两种传输方式下根据大气折射率结构常数的不同而不同；而在自由空间中传输时，强度并不会因传输方式的不同而不同.同时还可以看出，在大气湍流中传输时，斜程方式的光强分布比水平方式更集中；无论是在自由空间还是在大气湍流中传输，完全相干GSM光比部分相干GSM光的光强分布更集中.在湍流大气中传输时，对部分相干GSM光和完全相干GSM光的光强分布与其在自由空间中的光强分布进行对比可发现，部分相干GSM光的差别较小，由此可知部分相干GSM光的抗湍流特性优于完全相干GSM光，这与文献［3］中水平传输的结论一致.

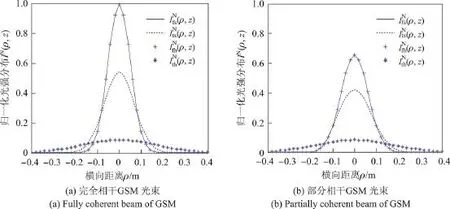
图1　完全相干和部分相干GSM光束在大气湍流中传输时的光强归一化分布Figure 1 Normalized intensity distribution of fully coherent and partially coherent beam of GSM transmitted in the turbulence

图2给出了不同天顶角条件下部分相干GSM光归一化光强的分布.计算选取参数如下：斜程传输时，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s；水平传输时，大气折射率结构常数（2）=1.7×10-14m-2/3.传输距离z=7 071 m，斜程传输时的高度为H=z cosθ+h0，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m，波长λ=650 nm.从图2中可以看出，天顶角越大，光强分布越分散；天顶角为0，即垂直传输时，光强分布最集中，光束扩展最小；水平传输时，光强分布最分散，扩展最严重.产生该结果的主要物理原因如下：当高度小于10 km时，大气折射率结构常数（h）随着高度的增加而减小；当高度大于10 km时，由于高空风速的影响会稍有增加再减小［7］，由此可知光束传输时的大气信道越靠近地面，受到的湍流影响越大，即天顶角越大，光束扩展就越严重，光强分布越分散.

图2　不同天顶角下部分相干GSM光在大气湍流中传输时的归一化光强分布Figure 2 Normalized intensity distribution of partially coherent beam of GSM transmitted in the turbulence with diferent zenith

图3给出了不同湍流强度下部分相干GSM光束传输时的光强归一化分布.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面风速vg=2.8 m/s，传输距离z=7 071 m，高度H=5 000 m，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m，波长λ=650 nm.由图3可以看出，在相同湍流条件下，光束斜程传输时的光强分布比水平传输时更集中，光强峰值更大，同时湍流强度越大，光束扩展越严重，光强分布越不集中.这是因为当光束在大气中传输时，大气折射率的随机起伏会导致波束出现相位畸变，使得光束在传输一定距离后产生光束扩展，从而导致光强分布更加分散，峰值光强也更弱，并且随机起伏越大，光束的扩展就更严重，光强会更弱.

在不同内、外尺度情况下，部分相干GSM光束在传输时的光强分布如图4所示.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s；水平传输时，大气折射率结构常数（2）=1.7×10-14m-2/3，传输距离z=7 071 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m，波长λ=650 nm.假设外尺度L0=10 m，对光束归一化光强分布进行分析，结果如图4（a）所示.从该图中可以看出，斜程传输方式的光强分布显然比水平方式更集中，光束扩展也更小，同时内尺度越小，强度分布越分散，光束扩展也越严重.同理假设内尺度l0=0.01 m，光束归一化光强分布如4（b）所示.由图4（b）可看出，在不同外尺度情况下，其归一化强度分布曲线非常接近，因此，在分析大气湍流对光束强度分布这一特性的影响时，可只考虑内尺度而忽略外尺度.产生该结果的主要物理原因如下：湍流内尺度越小，光束截面包含的小湍流漩涡越多，照射在这些漩涡上的光束会发生更严重的衍射，从而使光束的强度在空间和时间上出现的随机分布更严重，光强更分散.湍流外尺度越大，光束在接收面上的漂移越严重，而对扩展产生的影响很小.

图3　不同湍流强度下部分相干GSM光束传输时的光强归一化分布Figure 3 Normalized intensity distribution of partially coherent beam of GSM transmitted in diferent turbulence

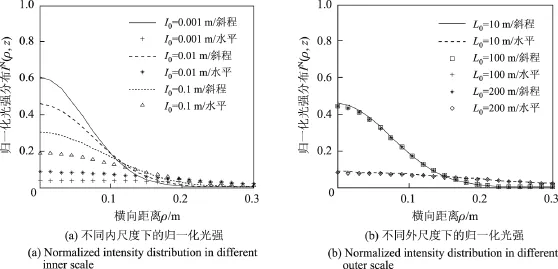
图4　不同内、外尺度下归一化光强分布情况Figure 4 Normalized intensity distribution of partially coherent beam of GSM transmitted in the turbulence with diferent inner and outer scale

在不同相干长度情况下，部分相干GSM光束在大气湍流和自由空间中传输时的光强分布如图5所示.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s，高度H=5 000 m；水平传输时，大气折射率结构常数（2）=1.7×10-14m-2/3，传输距离z=7 071 m，内尺度l0=0.01 m，外尺度L0=10 m，束腰宽度σs=0.05 m，波长λ=650 nm.从图5中可以看出，斜程传输时，相干长度越小，强度分布越分散，扩展越严重；在斜程传输时，相干长度越小，湍流中的传输曲线与自由空间中的传输曲线越接近，说明光束相干长度越小，光强受湍流的影响就越小.光强的强弱是受自由空间衍射和湍流共同决定的［15］，这里相干性越差，光强受湍流的影响越小，但光强变弱，这是由于光束受到的真空衍射的影响增大而导致的.

图5　不同相干长度下部分相干GSM光束在大气湍流中传输时的归一化光强分布Figure 5 Normalized intensity distribution of partially coherent beam of GSM transmitted in the turbulence with diferent coherence length

在不同湍流强度下，接收平面中心处部分相干GSM光束斜程传输时光强随束腰宽度的变化如图6所示.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面风速vg=2.8 m/s，传输距离z=7 071 m，高度H=5 000 m，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，波长λ=650 nm，横向距离ρ=0.从图6中可看出，斜程传输时，湍流强度越大，接收平面中心处的强度随着束腰宽度的变化幅度越大；随着束腰宽度的增大，强度先迅速减小，再逐渐增大，在束腰半径为0.019 m时光强最弱.观察式（8）可知，光强与束腰宽度有关，因此对其求偏导，可知存在一个极值点0.019，即可解释光强在该点时最弱.这一结论有助于在实际中针对不同应用选择光束束腰宽度大小.

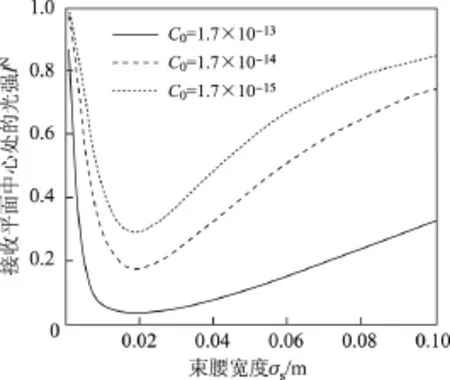
图6　不同湍流强度下部分相干GSM光束斜程传输时光强随束腰宽度的变化Figure 6 Normalized intensity distribution of partially coherent beam of GSM transmitted in diferent turbulence

图7给出了不同波长下部分相干GSM光束斜程传输时的光强归一化分布.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s，传输距离z=7 071 m，高度H=5 000 m，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m.从图7中可看出，斜程传输时光束的归一化光强随着波长的增大而变弱，说明光束波长越大，其归一化光强越弱，波长越短，光强越强.出现该结果可从两方面得到解释，1）大气对不同波长的光束有不同的吸收谱线，因此光束波长不同，在大气中传输时也会出现不同的衰减，其强度分布也不同.2）观察式（8）可知，光束归一化光强与波数k成正比，于是根据波数与波长的关系式可推出归一化光强与波长成反比.

图7　不同波长下部分相干GSM光束斜程传输时的光强归一化分布Figure 7 Normalized intensity distribution of partially coherent beam of GSM transmitted in the turbulence with diferent wavelength

3　GSM光束湍流大气中传输的光束扩展

图8给出了不同天顶角下相对束宽随传输距离的变化情况.计算选取参数如下：斜程传输时，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s；水平传输时，大气折射率结构常数（2）=1.7×10-14m-2/3，内尺度l0= 0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m；波长λ=650 nm.从图8中可以看出，在相同传输距离下，天顶角越大，相对束宽越大，即光束扩展所受湍流影响就越大；垂直向上传输时，相对束宽最小，光束的抗湍流能力最强，而水平传输时相对束宽最大，其抗湍流能力也最弱.这种情况可从大气折射率结构常数随高度的变化规律得到解释.

图9给出了不同湍流强度下部分相干GSM光束相对束宽随传输距离的变化情况.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面风速vg=2.8 m/s，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m，波长λ=650 nm.由图9可知，在不同湍流强度下，相对束宽随着传输距离的增大而增大，且湍流强度越大，其增长速度越快，光束扩展所受湍流的影响也就越大.这是因为光束受到大气折射率的影响，产生的波前相位畸变会随着传输距离的增加而严重，从而使得光束受到湍流的影响越大.同时还可以看出，在传输距离一定时，光束在斜程传输时的相对束宽总是比水平传输时要小，即光束以斜程方式传输时的抗湍流能力更强.这是因为斜程方式传输时的大气结构常数小于靠近地面的水平传输时的情况，所以光束斜程传输时受到的湍流影响较小.

图8　不同天顶角下光束相对束宽随传输距离的变化Figure 8 Relative beam width of the beam versus the transmitted distance with diferent zenith

图9　不同湍流强度下光束相对束宽随传输距离的变化Figure 9 Relative beam width of the beam versus the transmission distance with diferent turbulence

在不同内、外尺度条件下，相对束宽随传输距离的变化如图10所示.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s；水平传输时，大气折射率结构常数（2）=1.7×10-14m-2/3，相干长度σg=0.02 m，束腰宽度σs=0.05 m，波长λ=650 nm.假定外尺度L0=10 m，内尺度l0=0.01 m，光束相对束宽随传输距离的变化分别如图10（a）和（b）所示.对比图（a）和（b）可以看出，光束斜程传输时的相对束宽总是小于水平传输时的情况，即光束斜程传输的抗湍流能力总强于水平方式；内尺度越小，相对束宽越大，光束扩展受湍流的影响也越大，而外尺度对光束相对束宽的影响很小，可以忽略.

图11给出了不同相干长度下光束相对束宽随传输距离的变化情况.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s；水平传输时，大气折射率结构常数（2）=1.7×10-14m-2/3，内尺度l0=0.01 m，外尺度L0=10 m，束腰宽度σs=0.05 m，波长λ=650 nm.由图11可以看出，在相同传输距离下，相干长度越大，相对束宽越大，说明光束相干性越好，光束扩展受湍流影响越大，光束斜程传输时的抗湍流能力明显强于水平传输时的情况，这与图5所得结论一致.

图10　不同内、外尺度条件下相对束宽随传输距离的变化Figure 10 Relative beam width of the beam versus the transmission distance with diferent inner and outer scale

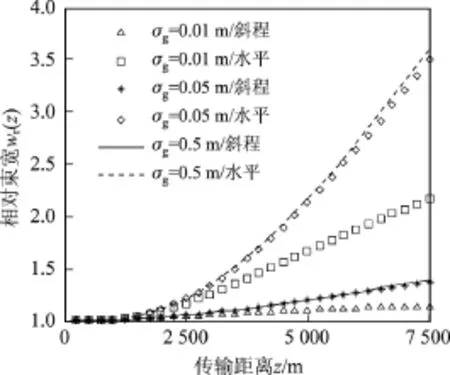
图11　不同相干长度下光束相对束宽随传输距离的变化Figure 11 Relative beam width of the beam versus the transmission distance with diferent coherence length

在不同湍流强度下，光束在斜程传输时相对束宽随束腰宽度的变化情况如图12所示.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2m，近地面风速vg=2.8m/s，传输距离z=z1=7 500 m，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，波长λ=650 nm.由图12可以看出，在相等湍流强度下，相对束宽随着束腰宽度的增大呈先增大后减小的趋势，且湍流越强，相对束宽峰值越大，相应的增加和减小速度也就更大.这里类似于图6，观察式（15）可知，相对束宽的大小与束腰宽度有关，于是对其求偏导，可知约在0.197处相对束宽达到最大.

在不同波长下，光束在斜程传输时相对束宽随传输距离的变化情况如图13所示.计算选取参数如下：斜程传输时，天顶角，发射机高度h0=2 m，近地面大气折射率结构常数C0=1.7×10-14m-2/3，近地面风速vg=2.8 m/s，内尺度l0=0.01 m，外尺度L0=10 m，相干长度σg=0.02 m，束腰宽度σs=0.05 m.由图13可以看出，在传输距离一定的条件下，波长越长，相对束宽越小，光束扩展受湍流影响越小，说明波长越长，抗湍流特性越强.该现象的产生是由于不同波长的光束在大气中传输时的衰减大小不同，对应的光束扩展则不同，进而相对束宽也会受到影响.同时由式（15）可知，光束的相对束宽ωr与波长λ成反比，因此波长越短，相对束宽就越大，所受湍流影响就越大.

图12　不同湍流强度下相对束宽随束腰宽度的变化Figure 12 Relative beam width of the beam versus the waist width with diferent turbulence

图13　不同波长情况下相对束宽随传输距离的变化Figure 13 Relative beam width of the beam versus the transmission distance with diferent lambda

4　结语

本文推导了斜程传输时部分相干GSM光束的归一化强度分布及相对束宽表达式，根据修正Von Karmon谱模型和ITU-R颁布的随高度变化的大气结构常数模型，对部分相干GSM光束在大气湍流中传输时的归一化强度分布和相对束宽进行数值计算与分析.结果表明：1）完全相干GSM光和部分相干GSM光在自由空间中的归一化强度分布与传输方式无关；2）部分相干光比完全相干光的抗湍流特性更好，同时斜程方式的抗湍流特性明显优于水平方式；3）光强随着湍流强度、天顶角、波长的增大而减弱，随着相干长度、内尺度的减小而减弱，从而导致束宽增大；4）相对束宽随着湍流强度、天顶角、相干长度的增大而增大，随着波长、内尺度的减小而增大，从而导致光束受湍流的影响变大.因此，在现实应用中应根据这些参数的影响状况来选取最优光束，这对于地空斜程路径的大气激光通信将具有重要的指导作用和现实意义.

［1］WU J.Propagation of Gaussian-Schell beam through turbulent media［J］.Journal of Modern Optics，1990，37（4）：671-684

［2］GREG G，EMIL W.Spreading of partially coherent beams in random media［J］.Journal of the Optical Society of America A-Optics Image Science and Vision，2002，19（8）：1592-1598.

［3］张逸新，王高刚.斜程大气传输激光束的平均光强与短期光束扩展［J］.红外与激光工程，2007，36（2）：167. ZHANG Y X，WANG G G.Average intensity and short-term beam spread of a laser beam propagating in a slant-path atmosphere［J］.Infrared and Laser Engineering，2007，36（2）：167.（in Chinese）

［4］ZHANG Y T，LIU L，WANG F，CAI Y J，DING C L，PAN L Z.Average intensity and spectral shifts of a partially coherent standard or elegant Laguerre-Gaussian beam beyond paraxial approximation［J］.Optical Quant Electron，2014，46：365-379

［5］李晓峰.星地激光通信链路原理与技术［M］.北京：国防工业出版社，2007：1-46.

［6］BORAH D K，VOELZ D G.Spatially partially coherent beam parameter optimization for free space optical communications［J］.Optics Express，2010，20（18）：20746.

［7］张晓欣，但有权，张彬.湍流大气中斜程传输部分相干光的光束扩展［J］.光学学报，2012，32（12）. ZHANG X X，DAN Y Q，ZHANG B.Spreading of partially coherent fat-topped beams propagating along a slant path in turbulent atmosphere［J］.Acta Optica Sinica，2012，32（12）.（in Chinese）

［8］DUAN M L，LI J H，WEI J L.Infuence of diferent propagation paths on the propagation of laser in atmospheric turbulence［J］.Optoelectronics Letters，2013，9（6）：1.

［9］李成强，张合勇，王挺峰，刘立生，郭劲.高斯-谢尔模光束在大气湍流中传输的相干特性的研究［J］.物理学报，2013，62（22）：224203. LI C Q，ZHANG H Y，WANG T F，LIU L S，GUO J.Investigation on coherence characteristics of Gauss-Schell model beam propagating in atmospheric turbulence［J］.Acta Physica Sinica，2013，62（22）：224203.（in Chinese）

［10］DAN Y Q，ZHANG B.Beam propagation factor of partially coherent fat-topped beams in a turbulent atmosphere［J］.Optics Express，2008，16（20）：15563.

［11］ANDREWS L C，PHILLIPS R L.Laser beam propagation through random media［M］.Bellingham：SPIE optical Engineering Press，2005：195.

［12］李晋红，吕百达.部分相干涡旋光束通过大气湍流上行和下行传输的比较研究［J］.物理学报，2011，60（7）：4205. LI J H，Lü B D.Comparative study of partially coherent vortex beam propagations through atmospheric turbulence along a uplink path and a downlink path［J］.Acta Physica Sinica，2011，60（7）：4205.（in Chinese）

［13］WEI L，LIU L R，SUN J F，YANG Q G，ZHU Y J.Change in degree of coherence of partially coherent electromagnetic beams propagating through atmosphere turbulence［J］.Optics Communications，2007，27（1）：1-8.

［14］TOMOHIRO S，ARISTIDE D，EMIL W.Mode analysis of spreading of partially coherent beams propagating through atmospheric turbulence［J］.Journal of the Optical Society of America AOptics Image Science and Vision，2003，20（6）：1094-1102.

［15］KOROTKOVA O，ANDREWS L C.PHILLIPS R L.Speckle propagation through atmospheric turbulence：efects of a random phase screen at the source［C］//Conference on Free-Space Laser Communication and Laser ImagingⅡ，2002：3-11.

（编辑：王雪）

Intensity and Expansion of Partially Coherent Beam Propagating in Slant and Horizontal Atmospheric Turbulence

KE Xi-zheng，WANG Wan-ting
School of Automation and Information Engineering，Xi'an University of Technology，Xi'an 710048，China

Based on the generalized Huygens-Fresnel principle，we derive the cross-spectral density function using the modifed von Karmon spectrum and atmospheric refractive-index structure constant issued by ITU-R.We also derive analytic expressions of intensity distribution and beam width of partially coherent Gaussian-Schell beam propagating in the atmosphere along slant and horizontal paths.The impact on the beam propagating in the two ways due to turbulence intensity，zenith，coherence length of the beam and other parameters are discussed.They are compared respectively from the perspective of normalized intensity distribution and relative expansion.The results show that the normalized intensity distribution of the beam in a free space along a horizontal path is the same as that along a slant path.The normalized intensity distribution is more concentrated，with the peak much stronger when zenith is smaller，while the efects of the turbulence becomeweaker.Impact on the zenith expansion，turbulence，coherence of the beam is almost consistent with the slant path.

partially coherent beam，slant path，normalized intensity distribution，relative beam width

O43

0255-8297（2015）02-0142-13

10.3969/j.issn.0255-8297.2015.02.004

2014-07-09；

2014-09-23

国家自然科学基金（No.61377080,No.60977054,No.61271110）；陕西省自然科学基础研究计划基金（No.2013JQ8011）；陕西省教育厅科研计划项目基金（No.2013JK1104）；陕西省工业攻关科技计划项目基金（No.2013K06-08）资助

柯熙政，教授，研究方向：无线激光通信，E-mail：xzke@263.net