面阵中降维Capon的二维DOA估计
蒋驰,张小飞,张立岑
南京航空航天大学电子信息工程学院,南京210016
面阵中降维Capon的二维DOA估计
蒋驰,张小飞,张立岑
南京航空航天大学电子信息工程学院,南京210016
提出了面阵中基于降维Capon的二维波达方向(direction of arrival,DOA)估计算法.先求得接受信号的协方差矩阵,再对其变换式进行谱峰搜索估计出一个参数,进而通过最小二乘估计出第2个参数.采用一维全局搜索实现二维DOA的联合估计,可避免二维Capon算法由二维谱峰搜索带来的巨大计算量,从而大大降低了计算复杂度,且角度估计性能非常接近于二维Capon算法.该算法既可以实现二维角度的自动配对,又可以精确地估计出相同方位角(或仰角)的信源,其优越性均可在文中得到验证.
面阵;波达方向估计;降维Capon
阵列信号处理在通信、雷达、声纳和医学等领域有着广泛的应用[1-5],并受到了高度重视.其本质是通过空间分散排列的传感器阵列和多通道接收可以获取信号的时域和空域等多维信息,同时利用这些信息来检测信号和提取参数,具有灵活、信号增益高、抗干扰能力强以及空间分辨能力好等诸多优点.在阵列信号处理中,波达方向(direction of arrival,DOA)估计无疑是一个非常重要的技术,已经成为研究的重点和热点.DOA估计方法主要包括多重信号分类(multiple signal classification,MUSIC)方法[6-7]、借助于旋转不变技术的信号参数估计(estimation of signal parameters via rotational invariance technique,ESPRIT)算法[8-10]、传播算子算法(propagator method,PM)[11]和Capon算法[12]等.
在DOA估计中,由于一维参数估计在实际应用中存在局限性,近年来二维DOA估计作为阵列信号处理的一个标志性方向成为学术界研究的热点[13-21],包含二维MUSIC算法[18]、二维ESPRIT算法[19]、二维PM算法[20]和二维Capon算法等.
二维Capon算法利用抑制噪声及非信源方向上的干扰,并根据信源方向上的信号功率不变的准则来准确估计二维DOA.该算法需要在二维参数空间中通过二维谱峰搜索过程估计DOA,计算量巨大,故在实际中难以应用.因此,本文对其进行改进,提出了一种适用于面阵情况下的降维Capon算法,以实现二维DOA的估计.该算法采用一维全局搜索实现二维DOA的联合估计,不但避免了二维Capon算法复杂的计算量,大大降低了计算复杂度,而且其角度估计性非常接近于二维Capon算法,此外还可以很好地实现二维角度的自动配对.本文推导了该算法的估计误差方差和克拉美罗界(Cramer-Rao bound,CRB).
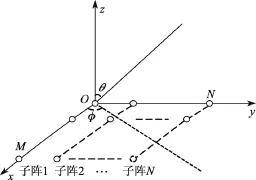
图1 均匀面阵的阵元结构[1]Figure 1 Structure of the uniform planar array[1]
1 数据模型
图1是一个M×N的矩形面阵,其中相邻阵元间距为d.考虑到远场信号的信源足够远,可以认为信号到达阵列时是平行波.假设噪声与信号独立,且为加性独立同分布的高斯噪声.假设有K个非相干信源,第k个信源对应的仰角和方位角分别表示为θk和φk,定义uk=sinφksinθk,vk=cosφksinθk.
矩形面阵中第1个子阵列的接收信号为x1(t)=Axs(t)+n1(t),其中Ax=[ax(v1),ax(v2),···,ax(vK)],而ax(vk)=[1,e-j2πdvk/λ,···,e-j2π(M-1)dvk/λ]T,[·]T表示转置,λ为信号波长. n1(t)为第1个子阵的加性高斯白噪声.s(t)∈CK×1为信源矢量.矩形面阵中第n个子阵的接收信号可以表示为xn(t)=AxΨn-1s(t)+nn(t),其中Ψ=diag(e-j2πdu1/λ,···,e-j2πduK/λ),diag(·)为对角化算子,nn(t)为第n个子阵的加性高斯白噪声.阵列的接收信号可以表示为
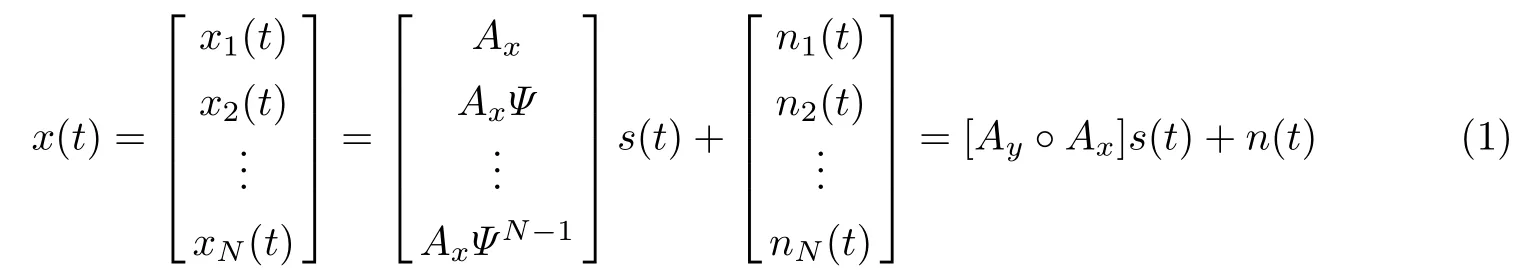
式中,Ay=[ay(u1),ay(u2),···,ay(uK)],ay(uk)=[1,e-j2πduk/λ,···,e-j2π(N-1)duk/λ]T,◦表示Khatri-Rao积,n(t)=[n1(t)T,n2(t)T,···,nN(t)T]T.Ay◦Ax=[ay(u1)⊗ax(v1),···,ay(uK)⊗ax(vK)].因此,式(1)也可以重新写为
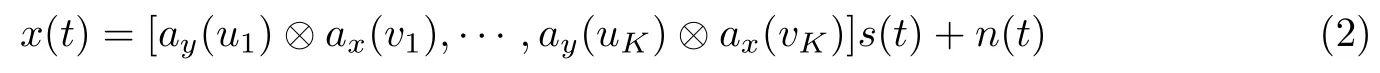
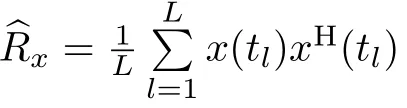
2 面阵下的二维DOA估计
2.1二维Capon算法
构造二维Capon空间谱函数为[1]

2.2降维Capon算法
降维Capon算法作为二维Capon算法的一种改进算法,采用一维全局搜索实现二维DOA的联合估计,可以大大降低计算复杂度[21].文献[21]针对二维Capon算法巨大的计算量,提出了一种应用于MIMO雷达系统的降维Capon算法.本文将降维Capon算法推广到面阵中实现二维角度的联合估计,并提出适用于面阵下二维DOA估计的降维Capon算法.
下面介绍本文提出的降维Capon算法的具体实现过程.定义
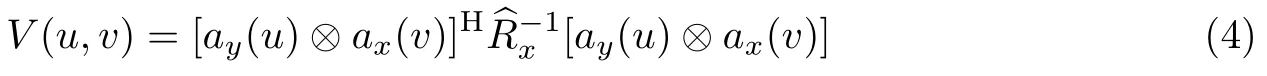
式(4)也可以表示为[21]

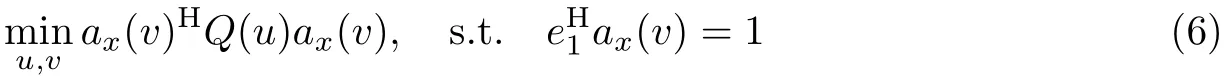
构造代价函数L(θ,φ)=ax(v)HQ(u)ax(v)-λ,其中λ为一个常量,对ax(v)求导,有
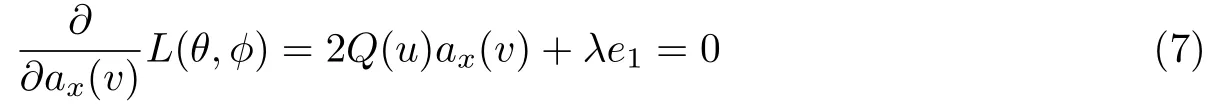
由式(7)可得ax(v)=µQ(u)-1e1,其中µ为一个常量.由于,结合ax(v)= µQ(u)-1e1,可得.代入求得ax(v)为


式(9)也可以写为
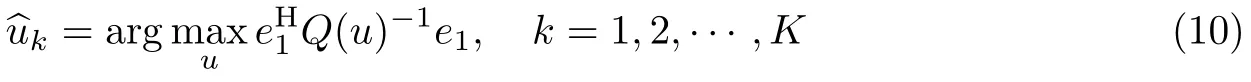
对u在u∈[-1,+1]内进行全局搜索,找到Q(u)-1第(1,1)个元素的最大值.根据式(8),通过最大的K个峰值对应的uk(k=1,···,K)得到K个矢量

式中,angle(·)为取复矩阵中每个元素的相位,可写成gk=[0,2πdvk/λ,···,(M-1)2πdvk/ λ]T=vkq,其中q=[0,2πd/λ,···,(M-1)2πd/λ]T,用最小二乘法估计vk.归一化导向矢量的估计值为,然后根据式(11)由归一化的得到
现在用最小二乘拟合去估计vk.最小二乘法为,其中表示F范数,P=[1M,q],ck=[ck0,vk]T∈R2×1是一个未知的参数矢量,ck0为参数误差估计值.通过最小二乘结果,可得信源方向的仰角和方位角分别为
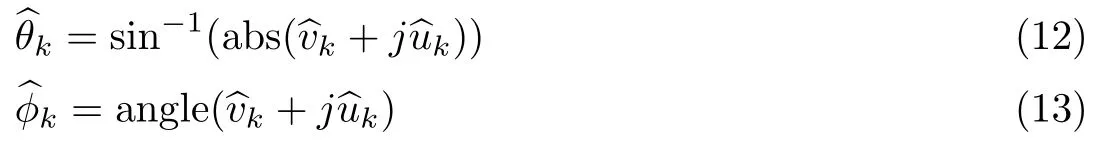
至此已明确给出了在面阵中使用降维Capon算法来进行二维DOA联合估计的方法.算法的主要步骤如下:
步骤2通过全局搜索,找到Q(u)-1第(1,1)个元素中最大的K个峰值,得到对应的uk(k=1,···,K)的估计值,根据式(8)得到,然后利用最小二乘得到vk(k=1,···,K)的估计值,其计算复杂度为O(M3N3+n1[N2(M+1)+2(M2N3+MN3+N3+N2+N)]).
2.3复杂度分析
相对于使用谱峰搜索方法的二维Capon算法,本文算法的计算复杂度很低.该算法的主要计算复杂度为O(LM2N2+M3N3+n1[N2(M+1)+2(M2N3+MN3+N3+N2+ N)]),其中n1为一维全局范围[-1,1]内搜索u的步数.二维Capon算法的计算复杂度为O,其中n2为全局范围[-90◦,90◦]内搜索θ和φ的步数.
2.4算法优点
1)可以实现自动配对的二维角度估计;
2)只需一维全局搜索,而二维Capon算法需要二维全局搜索;
3)角度估计性能接近于二维Capon算法;
4)可以在相同方位角(或仰角)的信源下有效地工作.
以上这些优点可以在下文的仿真结果分析中得到验证.
3 性能分析
本小节分析了本文算法的角度估计性能.建立本算法的二维DOA估计的大样本均方误差(mean-square error,MSE),同时推导二维DOA估计的CRB.本小节旨在寻找下面公式的最小值],其中限制ax(v)的第1个元素为1.

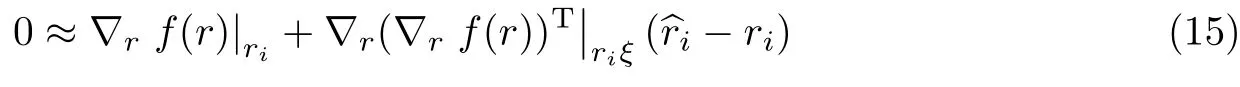
式中,riξ表示由ri和之间线段上的一些值组成的矢量.根据式(15)可得矢量ri的估计误差

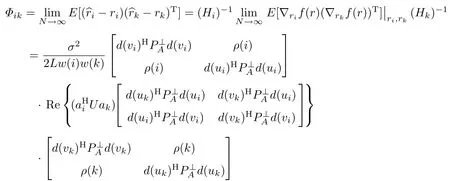
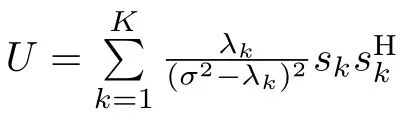
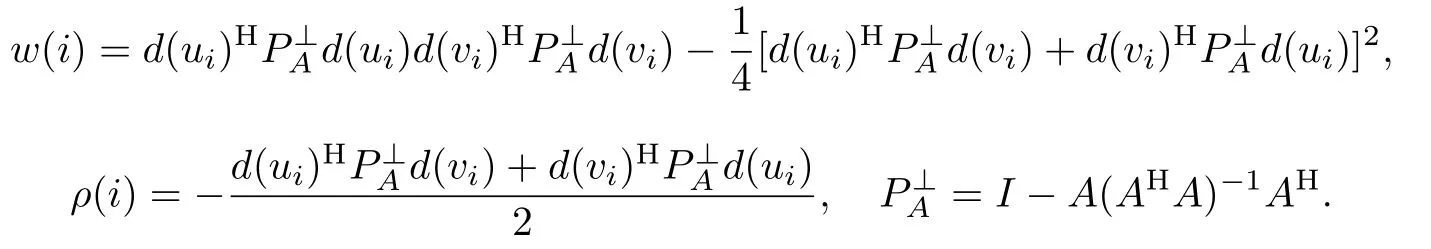
由式(17)可知变量uk的估计误差为=Φkk(1,1),而vk的估计误差为= Φkk(2,2).uk和vk的估计误差的协方差矩阵为E[∂vk∂uk]=Φkk(2,1).
根据式(12)和(13),得到方位角和仰角的MSE分别为
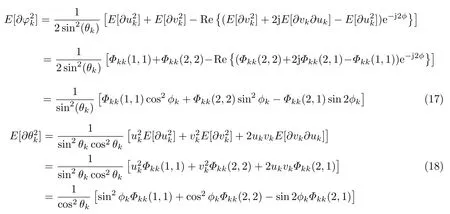
下面给出均匀矩阵下角度估计的CRB[22]

4 仿真结果分析
对降维Capon算法估计二维DOA进行仿真,并且用角度的求根均方误差(root mean square error,RMSE)清晰直观地反映本文算法的性能.至此,定义角度的RMSE为

式中,T为仿真次数,ωkm为第m次仿真中第k个信源仰角(或方位角)的估计值,K为信源数目,ωk为仰角(或方位角)的精确值.
为表述方便,定义目标数目为K,快拍数为L,面阵阵元数为M×N.不失一般性,以下仿真过程中均设N=8.
4.1确定信噪比(signal to noise ratio,SNR)的情况下3个不同信源的仿真
当SNR为5 dB时,3个不同信源的仿真结果如图2所示,其中M=8,3个不同信源的仰角和方位角分别为(10◦,20◦)、(20◦,30◦)、(30◦,40◦),可以看出该算法能有效地估计出仰角和方位角.
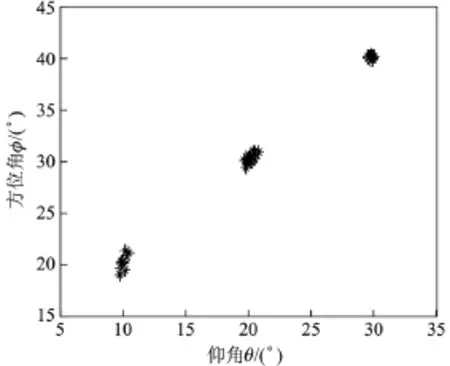
图2 降维Capon算法的二维DOA估计(L=100,M=8,K=3,N=8和SNR=5 dB)Figure 2 2D DOA estimation performance with RD-Capon algorithm(L=100,M=8,K=3,N=8 and SNR=5 dB)
4.2不同快拍数情况下的角度估计性能仿真
图3针对不同快拍数情况下的角度估计性能进行仿真.从图3中可以看出,仰角和方位角的σRMSE值随着快拍数的增加而变小,算法的性能也变好.因为采样数据随着快拍数的增加而增加,从而得到更加精确的协方差矩阵,所以得到的角度估计性能越好.

图3 不同L情况下的仰角和方位角的估计性能(M=6,N=8和K=3)Figure 3 Elevation and azimuth estimation performance with diferent L(M=6,N=8 and K=3)
4.3不同阵元数情况下的角度估计性能仿真
图4仿真了不同阵元数情况下的角度估计性能.从图4中可以看出,仰角和方位角的σRMSE值随着阵元数的增加而变小,算法的性能也得到提升,这是因为阵元数的增加而使分集增益增加的缘故.
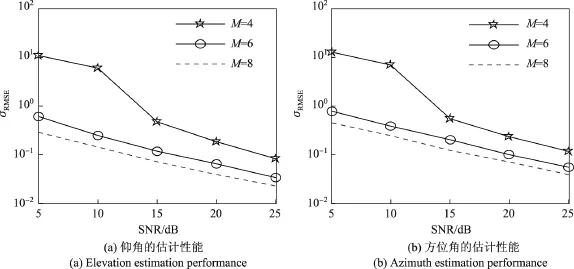
图4 不同M情况下的仰角和方位角的估计性能(L=100,N=8和K=3)Figure 4 Elevation and azimuth estimation performance with diferent M(L=100,N=8 and K=3)
4.4不同信源数情况下的角度估计性能仿真
图5展示了不同信源数情况下的角度估计性能.从图5中可以看出,仰角和方位角的σRMSE值随着信源数的增加而变大,算法的性能也变差.这是因为信源数增加会导致信源间的干扰变大,角度估计性能变差.
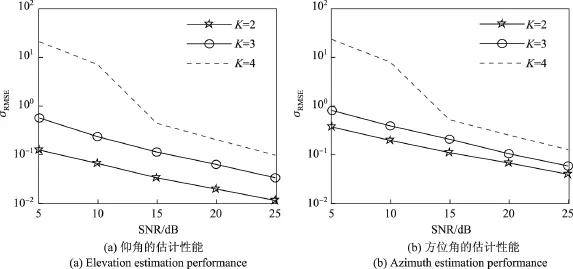
图5 不同K情况下的仰角和方位角的估计性能(L=100,M=6和N=8)Figure 5 Elevation and azimuth estimation performance with diferent K(L=100,M=6 and N=8)
4.5与二维Capon算法估计二维DOA的性能以及CRB的对比
图6是本文提出的降维Capon算法和二维Capon算法估计二维DOA的性能对比图,并把这两种算法的性能与CRB进行比较.显然,本文算法(RD-Capon)在同时估计仰角和方位角情况下的性能与二维Capon算法相近,且在较高信噪比情况下非常逼近于二维Capon算法.尽管该算法为了降低计算复杂度而牺牲了部分性能,但在图6中可以清晰地看出,只要信噪比稍大一些,该算法性能和二维Capon算法性能非常逼近,因此较二维Capon算法有更宽广的应用范围.
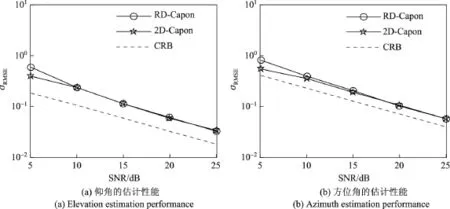
图6 不同算法的仰角和方位角的估计性能(L=100,M=6,N=8和K=3)Figure 6 Elevation and azimuth estimation performance with diferent algorithm(L=100,M=6,N=8 and K=3)
4.6相同仰角的信源进行角度估计的性能仿真
如图7所示,本文算法可以很好地估计出相同仰角的信源.
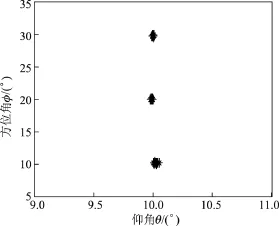
图7 相同仰角情况下信源的估计(L=100,M=8,N=8,K=3和SNR=30 dB)Figure 7 2D DOA estimation with the same elevation source(L=100,M=8,N=8,K=3 and SNR=30 dB)
4.7相同方位角的信源进行角度估计的性能仿真
如图8所示,本文算法可以准确地估计出相同方位角的信源.因为该算法是估计角度对(θk,φk)的综合信息uk和vk,即使θk(或φk)相同,本文算法依然能很好地工作.
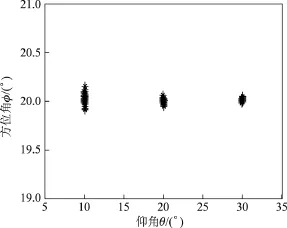
图8 相同方位角情况下信源的估计(L=100,M=8,N=8,K=3和SNR=30 dB)Figure 8 2D DOA estimation with the same azimuth source(L=100,M=8,N=8,K=3 and SNR=30 dB)
5 结语
本文提出了一种应用在面阵下的二维DOA联合估计算法––降维Capon算法.该算法采用一维全局搜索实现二维DOA的联合估计,由于只需一维搜索,成功地避免了二维Capon算法由谱峰搜索过程带来的的巨大计算量,大大降低了复杂度,同时性能非常接近于二维Capon算法估计性能;也可以实现二维角度的自动配对;还可以精确地估计出相同方位角(或仰角)的信源.因此,该算法更加高效,适用范围也更加广泛.
[1]张小飞,汪飞,陈伟华.阵列信号处理的理论与应用[M].2版.北京:国防工业出版社,2013.
[2]NAIDU P S.Sensor array signal processing[M].[S.l.]:CRC Press,2010.
[3]KIM J M,LEE O K,YE J C.Compressive MUSIC:revisiting the link between compressive sensing and array signal processing[J].IEEE Transactions on Information Theory,2012,58(1):278-301.
[4]胡增辉,朱炬波,何峰,梁甸农.互耦条件下均匀线阵DOA盲估计[J].电子与信息学报,2012,34(2):382-387. HU Z H,ZHU J B,HE F,LIANG D N.Blind DOA estimation in the presence of mutual coupling using uniform linear array[J].Journal of Electronics&Information Technology,2012,34(2):382-387.(in Chinese)
[5]闫锋刚,刘帅,金铭,乔晓林.基于降维噪声子空间的二维阵列DOA估计算法[J].电子与信息学报,2012,34(4):832-837. YAN F G,LIU S,JIN M,QIAO X L.2-D DOA estimation method based on dimension descended noise subspace[J].Journal of Electronics&Information Technology,2012,34(4):832-837.(in Chinese)
[6]邵华,苏卫民,顾红,王灿.基于稀疏互质电磁矢量阵列的MUSIC算法[J].电子与信息学报,2012,34(9):2033-2038. SHAO H,SU W M,GU H,WANG C.MUSIC algorithm based on sparse coprime electromagnetic vector arrays[J].Journal of Electronics&Information Technology,2012,34(9):2033-2038.(in Chinese)
[7]李建峰,张小飞,汪飞.基于四元数的Root-MUSIC的双基地MIMO雷达中角度估计算法[J].电子与信息学报,2012,34(2):300-304. LI J F,ZHANG X F,WANG F.Quaternion root-MUSIC algorithm for angle estimation in bistatic MIMO radar[J].Journal of Electronics&Information Technology,2012,34(2):300-304.(in Chinese)
[8]ZHENG G,CHEN B,YANG M.Unitary ESPRIT algorithm for bistatic MIMO radar[J].Electronics Letters,2012,48(3):179-181.
[9]BENCHEIKH M L,WANG Y.Joint DOD-DOA estimation using combined ESPRIT-MUSIC approach in MIMO radar[J].Electronics Letters,2010,46(15):1081-1083.
[10]ZOLTOWSKI M D,HAARDT M,MATHEWS C P.Closed-form 2D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT[J].IEEE Transaction on Signal Process,1996,44(1):326-328.
[11]MARCOS S,MARSAL A,BENIDIR M.The propagator method for source bearing estimation[J]. Signal Processing,1995,42(2):121-138.
[12]张保锋.几种DOA估计算法的性能分析[J].现代电子技术,2003(9):35-37. ZHANG B F.Performance of several algorithm of DOA[J].Modern Electronic Technology,2003(9):35-37.(in Chinese)
[13]杨德森,陈欢,时胜国.基于MUSIC算法的水下噪声源近场高分辨定位方法[J].哈尔滨工程大学学报,2011,32(8):1019-1023. YANG D S,CHEN H,SHI S G.A near-feld and high-resolution localization method of an underwater noise source based on a MUSIC algorithm[J].Journal of Harbin Engineering University,2011,32(8):1019-1023.(in Chinese)
[14]WU Y T,LIAO G S,SO H C.A fast algorithm for 2-D direction-of-arrival estimation[J].Signal Process,2003,83(8):1827-1831.
[15]ZHANG X F,LI J F,XU L Y.Novel two-dimensional DOA estimation with L-shaped array[J].EURASIP Journal on Advances in Signal Processing,2011(1):1-7.
[16]ZHANG X,WU H,LI J,XU D.Computationally efcient DOD and DOA estimation for bistatic MIMO radar with propagator method[J].International Journal of Electronics,2012,99(9):1207-1221.
[17]ZHANG X,XU L,XU L,XU D.Direction of departure(DOD)and direction of arrival(DOA)estimation in MIMO radar with reduced-dimension MUSIC[J].IEEE Communications Letters,2010,14(12):1161-1163.
[18]蔡晶晶,李鹏,赵国庆.RD-MUSIC的二维DOA估计方法[J].西安电子科技大学学报,2013,40(3):81-86. CAI J J,LI P,ZHAO G Q.Two-dimensional DOA estimation with reduced-dimension MUSIC[J].Journal of Xi'an Electronic and Science University,2013,40(3):81-86.(in Chinese)
[19]LAVATE T B,KOKATE V K,SAPKAL A M.Performance analysis of MUSIC and ESPRIT DOA estimation algorithms for adaptive array smart antenna in mobile communication[C]//2010 Second International Conference on Computer and Network Technology(ICCNT),2010:308-311.
[20]LI J,ZHANG X,CHEN H.Improved two-dimensional DOA estimation algorithm for two-parallel uniform linear arrays using propagator method[J].Signal Processing,2012,92(12):3032-3038.[21]ZHANG X,XU D.Angle estimation in MIMO radar using reduced-dimension Capon[J].Electronics Letters,2010,46(12):860-861.
[22]STOICA P,NEHORAI A.Performance study of conditional and unconditional direction-of-arrival estimation[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1990,38(10):1783-1795.
(编辑:秦巍)
Two-Dimensional DOA Estimation for Planar Array via Reduced-Dimension Capon
JIANG Chi,ZHANG Xiao-fei,ZHANG Li-cen
College of Electronic Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
This paper discusses estimation of two-dimensional(2D)direction of arrival(DOA)for a planar array,and derives a reduced-dimension Capon(RD-Capon)algorithm. The frst parameter is obtained by searching the spectrum peak of transformation of the covariance matrix,obtained from the received signal.The second parameter is estimated using least squares.The algorithm uses one-dimensional global search to achieve a joint estimation of 2D DOA.This algorithm based on one-dimension local searches can avoid high computational cost within 2D-Capon algorithm by spectrum peak search,with the performance close to the 2D-Capon algorithm.The proposed algorithm can obtain automaticallypaired 2D DOA estimation for planar array.It works well for the sources with the same azimuth(or elevation).Simulation results verify the usefulness of the algorithm.
planar array,direction of arrival(DOA)estimation,reduced-dimension Capon(RD-Capon)
TN92
0255-8297(2015)02-0167-11
10.3969/j.issn.0255-8297.2015.02.006
2014-04-03;
2014-10-14
国家自然科学基金(No.61371169);江苏省博士后科研项目基金(No.1201039C);中国博士后基金(No.2012M521099);江苏高校优势学科建设工程项目基金;中央高校基本科研业务费专项资金(No.NZ2012010);南京航空航天大学研究生创新基地(实验室)开放基金(No.kfjj120115)资助
张小飞,教授,博导,研究方向:阵列信号处理、通信信号处理、移动通信技术等,E-mail:zhangxiaofei@nuaa.edu.cn

