一种高精度低负载的可用带宽测量机制

周逸秋，陈兵，钱红燕，吕宗磊

1.南京航空航天大学计算机科学与技术学院，南京210016 2.中国民航大学中国民航信息技术科研基地，天津300300

一种高精度低负载的可用带宽测量机制

周逸秋1，陈兵1，钱红燕1，吕宗磊2

1.南京航空航天大学计算机科学与技术学院，南京210016 2.中国民航大学中国民航信息技术科研基地，天津300300

端到端的可用带宽是网络测量的重要性能指标之一.针对现有的大多数测量工具及方法在估算可用带宽前需要大量时间分析和测量等问题，在全面分析了网络中背景流特征的基础上，提出一种高精度低负载的可用带宽测量机制.该机制考虑了高速网络环境中丢包的情况，建立网络利用率与探测速率间的关系模型，结合扩展卡尔曼滤波实时获得最新的端到端的可用带宽.该机制不需要事先知道瓶颈链路容量，探测速率可低于可用带宽，降低了突发背景流对测量的影响.数值模拟表明，所提出的机制能快速响应突发背景流，准确高效地测得端到端的可用带宽.

可用带宽；突发背景流；扩展卡尔曼滤波

随着计算机网络规模的不断扩大，网络流量急剧增长，各种应用层出不穷，对网络带宽的需求也越来越大.在实时、多跳、高速的网络环境下，通过网络测量及时了解网络行为特征显得尤为重要.端到端路径上的网络可用带宽作为网络性能指标的重要参数之一，受到了越来越多的关注.它不仅能进行流量和拥塞控制，优化覆盖网络路径以及提高网络利用率，还有助于及时发现并探测网络故障和攻击，提高网络服务质量（quality of service，QoS）.

网络流量的动态性导致无法直接测量端到端的可用带宽，同时由于背景噪声等因素的干扰，现有的基于探测间隔模型（probe gap model，PGM）和探测速率模型（probe rate model，PRM）的测量方法低估了可用带宽，且无法对突发背景流做出快速的响应.本文针对双端测量环境以及大多数测量工具不适合实际跟踪可用带宽的问题，提出一种高精度低负载的可用带宽测量机制.

1　相关研究

现有的可用带宽测量方法大多依赖于瓶颈分隔原理的液体流模型［1］，该模型假设背景流无限小且速率保持稳定.文献［2］指出Internet中的背景流具有突发性，无法准确捕捉动态流量，低估了可用带宽.文献［3］使用隐马尔科夫模型将探测包对分布建模，从而快速且非侵扰地测得可用带宽，提高了可用带宽的精度.文献［4］认为端到端路径上30%的链路处于拥塞时，测得的可用带宽的平均误差达到10%，于是文献［5］提出使用K-means算法来减少测量误差.文献［6］基于“自拥塞”的概念，提出降速探测包列测量法（self-loading decreasling rate train，SLDRT），通过构造靠背的负载包和速率递减的探测包组成的探测包列，分析接收端获得的单向时延变化，当单向时延下降后趋于稳定状态时的发送速率为可用带宽.该方法在多紧链路和突发背景流下精度较高，但在寻找单向时延的转折点时引入了过多的探测包，对网络造成一定的影响.文献［7］提出一种自适应的高精度可用带宽测量算法FPU-ABM，该方法构造六包组的探测包列，利用在瓶颈链路前后测得时间间隔的变化来估计可用带宽，并根据发送速率与可用带宽之间的关系动态调整速率，从而减少网络负载，提高测量速度；但这种方法需要利用Pathneck［8］测得瓶颈链路的位置及容量，且只对测得的可用带宽样本取加权平均，使得测量结果精度不高.文献［9］基于卡尔曼滤波（Kalman filter，KF）算法提出一种实时可用带宽测量方法（bandwith available in realtime，BART），计算探测包列间的时间间隔张力ε（strain）作为KF的测量变量，用新的测量变量更新前一次系统状态，从而得到最新的可用带宽.在具体测量过程中，通过调整端到端路径上的不同网络状况来调整过程噪声（Q），从而获得了较好的性能；除此之外，使用累积和的方法应对突发背景流，使其快速响应突发背景流.该方法在突发背景流的网络环境下性能较好，但精度完全取决于Q，在一定程度上增加了网络负载和测量时间，且没有考虑在高速网络环境下存在丢包的情况，因此在极度拥塞的网络路径上测得的可用带宽比实际值高.本文基于BART的基本思想，提出一种高精度低负载快速测量可用带宽的机制，考虑网络中突发背景流和丢包的情况，建立网络利用率和探测速率间的关系模型，结合扩展卡尔曼滤波将网络利用率作为测量变量将可用带宽和瓶颈容量作为系统状态，实时估算更新可用带宽.

2　测量模型

2.1问题分析

Internet环境下测量可用带宽面临的挑战如下：

1）由于PGM模型中的假设条件在Internet中不成立，基于该模型的测量方法低估了可用带宽［10］.

PGM模型假设紧链路和窄链路一致，而在Internet中突发背景流的影响导致瓶颈链路的位置不断变化，且可能存在多跳紧链路.除此之外，该模型需要事先知道瓶颈容量C，这在Internet中无法直接获得.文献［11］在探测前使用Pathneck测得瓶颈容量，但此工具将ICMP类型数据包作为探测包，在传输过程中可能被某些路由器阻止.文献［12］也指出，Pathneck工具的测量数据并非可用带宽，而是处于可用带宽与路径容量间的渐进扩散率（asymptotic dispersion rate，ADR）.

2）基于PRM的测量方法所测的可用带宽不能超过源节点的最大发送速率［13］.

假设发送端在1 ms内发送1000 Byte的数据包，那么被测网络的瓶颈带宽就不能超过8 Mbit/s，否则数据包之间将不可能产生时间间隔.随着网络技术的不断发展，目前的网络已经达到千兆的带宽，并向更高的传输速率发展，因此该测量模型无法在高速网络环境下使用.这是因为本机制根据网络路径利用率与探测速率间的线性关系估计可用带宽，其测量范围不受源节点最大发送速率的限制.

3）Internet中背景流具有突发性.瓶颈链路的容量和位置是动态变化的，从而造成了可用带宽的动态性，这需要采用一定的机制来缓和突发背景流给测量结果带来的偏差.本机制采用最优化自回归数据处理算法EKF［14］，从一组包含噪声的测量序列中预测出最接近于实际值的可用带宽.

4）低精度的时间戳，增大可用带宽的测量误差.目前，很多测量工具通过接收端探测包的时间分布.如果最小的时间精度比测量时间间隔大，那么可获得时间间隔是最小时间精确度；如果比测量时间间隔小，那么认为数据包同时到达.因此，低精度的时间戳使得测得的可用带宽误差不断加大，收敛速度也相应减慢.本机制通过比较探测包列中各探测包的单向时延作为EKF的测量变量，防止低精度时间戳对可用带宽精度的精度造成影响.

5）在高速网络环境下，丢包影响可用带宽的精度.随着探测速率的增加，路由器缓冲区队列溢出产生丢包现象，而大多测量方法通常假设节点的缓冲区无限大，而没有考虑丢包的情况，影响了测量精度.本机制没有丢弃整个探测包列，而是通过探测包列中IP包的标识位找到邻居节点的测量值，用该值代替当前丢失节点的测量值.

2.2数学模型

本节在多跳链路下分析测量模型，根据排队论的思想将端到端路径中的每条链路看作一个队列，则队列l的利用率ul可表示为

式中，πl表示队列l为空的概率.

假设L个队列不相关，则端到端的网络路径利用率可以表示为

若探测包以探测速率r通过所测网络，则网络路径利用率可以表示为

当式（3）中的Tq＞0时

式（4）的一阶近似值为

由式（5），建立网络路径利用率u（r）和探测速率r之间的关系，得到拟合后的线性关系如图1所示.

图1　理想情况下u（r）与r间的线性关系Figure 1 Ideally，the linear relationship between u（r）and r

当探测速率r等于可用带宽A时，网络路径利用率为100%，此时对应的探测速率即为可用带宽，可表示为

由于网络中存在噪声、小数据集等影响网络利用率波动的因子，在探测周期内测得的网络利用率极其不规律［15］.因此，Internet中网络利用率u（r）和探测速率r间是一种动态的非线性关系，如图2所示.

图2　Internet中u（r）与r的非线性动态关系Figure 2 Non-linear relationship between u（r）and r in Internet

3　测量机制

根据第2节的分析，在Internet下，网络利用率与探测速率是一种动态的非线性关系，在无法获得背景流速率的情况下，如何对动态系统中的可用带宽进行实时测量？本文将此问题看作系统状态空间模型，建立观测变量和系统内部状态之间的关系，其中系统状态是非直接可测的，而系统状态及观测过程都不可避免受噪声的影响，使用扩展卡尔曼滤波法估计可用带宽.该方法实时而快速，且接收端无需发送应答包，也不必存储历史值，就能及时捕捉动态网络行为，解决了现有的测量工具在得到可用带宽前需要大量时间分析和测量的问题，适合实时跟踪可用带宽.

3.1扩展卡尔曼滤

扩展卡尔曼滤波可概括为：在滤波值附近，应用泰勒展开算法将非线性系统展开，对展开式进行一阶线性化截断而忽略其余高阶项，于是将原系统变成线性系统，再利用标准卡尔曼滤波对系统线性化模型进行滤波.标准卡尔曼滤波以最小均方误差为最佳估计准则，采用状态空间模型并根据前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，获得当前时刻的估计值.主要包括两个过程：一是时间更新，即利用时间更新方程建立对当前状态的先验估计，及时向前推算当前状态变量和误差协方差估计值，以便为下一个时间状态构造先验估计值；二是状态更新，即在预估过程的先验估计值及当前测量变量的基础上，利用测量更新方程对当前状态的改进的后验估计.

时间更新方程［14］如下：

状态更新方程［14］如下：

3.2探测包列

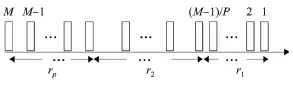
图3　探测包列Figure 3 Structure of probing packets

本文构造探测包列后，分别测试了周期、泊松、均匀、帕累托4种抽样方式.实验表明使用泊松分布时误差最小，呈指数分布的探测不会严重影响链路的负载，且平均误差总低于0.07，于是，本机制采用泊松分布的抽样方式.

在不同链路负载的网络环境下，探测包列的长度和包的大小影响可用带宽的测量.实验表明，当探测包列长度小于150时，测得网络利用率的误差较大；当探测包列长度大于150时，平均误差约为0.06.为了权衡可用带宽的精确度与测量时间，本文探测包列长度为200.不同探测包的长度也影响测量误差，经多次实验发现：40字节、100字节的探测包使得测量误差较大，500字节、1000字节、1500字节的探测包得到的精确度相似.为尽可能地减少发送探测包列中的探测包以及增大包间的时间间隔，本文选择1500 B大小的探测包.

3.3估计网络路径利用率

假设在多跳链路环境下，源端发送带有时间戳的探测包列.当一组探测包列到达接收端时，可以得到一组单向时延.在单向时延集合｛D｝中没有经历排队时延的探测包的单向时延最小，由此可以推测出比最小单向时延大的探测包在背景流的影响下经历了排队时延，那么网络路径利用率可以表示为

在探测的过程中，会出现网络拥塞和节点缓冲区队列溢出等情况，如果接收端的探测包列每组探测包列的数目不等于（M-1）/P，那么探测过程中就会出现丢包.通过IP包中的标识找到当前丢失节点的邻居节点，并以邻居节点的di代替丢失的数据包在端到端路径上的单向时延，从而获得网络利用率.

3.4算法设计

本机制将主动探测与扩展卡尔曼滤波算法相结合，在新的测量变量的基础上更新系统状态，实时获得最新的可用带宽.

本文将测得的网络利用率u（r）作为扩展卡尔曼滤波算法中的测量变量zk，可表示为

考虑到高阶线性化使算法变得复杂，本机制使用一阶Taylor把非线性状态空间模型展开，得到标准卡尔曼滤波中的线性空间状态模型

式中，uk为输入控制变量.当以一种方式改变系统状态时，本机制中的输入控制变量是探测包的探测速率.由于探测速率只对瓶颈链路造成瞬时拥塞而对系统状态的影响较小，本机制将其忽略.

假设w（k）～η（0，Q）、v（k）～η（0，R），

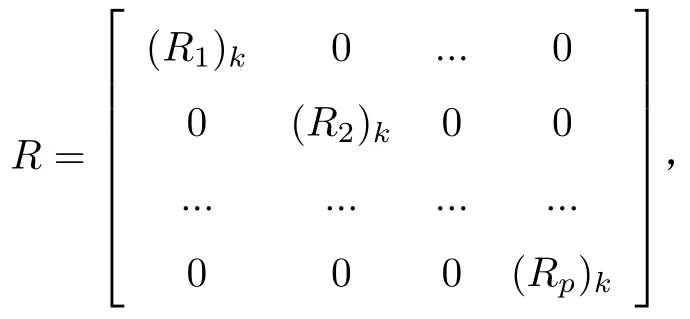
结合扩展卡尔曼的估计和纠正两个阶段的公式，可以估计得到α、β，根据式（7）实时得到可用带宽A，即为图中的转折点.伪代码如下：

Algorithm 1 Our mechanism Initialization /*初始化x初始化系统初始状态b x、可用带宽估计值bA、估计误差协方差矩阵bP、最大探测速率rmax、过程噪声Q、测量噪声探测包列中探测包的数目M、组数P、每组实际收到的探测包响应报文Mp；*/ Set b x= ? ? ,R,M=0,P=0,L=1500B,N=200；Process：①While（true）/*发送端以泊松分布速率［0,rmax］间发送探测包*/②x=unifrnd（0,rmax）,rp=poissrnd（lambda）；/*由式（13）得到网络利用率u（r）*/③u（r）=SendProbingPackets（rp）；/*接收端接收探测包列后，如果每组中探测包的数目不等于M-1?α β,bA=0,bP,rmax,Q= ?λ0 0λP，则存在丢包现象，那么就要找到丢包的位置，用邻居节点的u（r）代替.*/④If（Mp6=M-1P），用邻居节点的u（r）；/*根据扩展卡尔曼滤波计算更新可用带宽*/⑤xk=f（xk-1+uk-1）+wk-1,zk=h（xk+uk）+vk；⑥Fk|k= h∂f（xk,uk）i i∂xk xk=b xk|k,uck=b uck,Hk|k-1= h∂h（xk,uk）∂xk xk=b xk|k-1；⑦Prediction b xk|k=b xk|k-1+Kk xk|k-1=Fk|k-1b xk-1|k-1,Pk|k-1=Fk-1|k-1Pk-1|k-1FT k-1|k-1+Qk-1；⑧correction b i-1 Pk|k=?I-KkHk|k-1 ?Pk|k-1；?zk-h?b xk|k-1,uk?? Kk=Pk|k-1HT k|k-1 h Hk|k-1Pk|k-1HT k|k-1+Rk⑨bA= ?α β ?；⑩If（r 6bA）,Wait（）,Goto（1）；else Goto（3）；End R、

4　实验

MATLAB的库函数能简单快速地求解扩展卡尔曼滤波算法中的非线性方程，且擅长建模，于是本节使用MATLAB来验证突发背景流下该机制可用带宽的测量精度.分别编写程序产生背景流，模拟类似NS2产生的端到端网络路径、探测序列、背景流的发送和接收端及路由器，测量不同场景下各种参数（如Q、M、P）对其精确度的影响，选出不同场景下最合适的参数；其次在各参数配置相同的情况下，与使用卡尔曼滤波的BART测量方法进行对比.网络拓扑如图4所示，该拓扑是单瓶颈链路，与BART中的拓扑类似，端到端的网络路径的瓶颈链路位于两个路由器间.

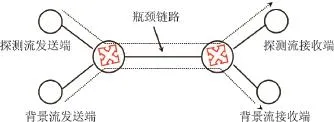
图4　网络拓扑图Figure 4 Topology of simulation

瓶颈链路容量C［10 Mbit/s，100 Mbit/s］可用体现所测网络不同的负载情况，探测包列中每组探测包的速率在［1 Mbit/s，20 Mbit/s］内服从泊松分布，探测包列的长度N为200，探测包的大小S为1500B.

式（18）用均方差来衡量可用带宽的精度

4.1M和P对可用带宽精度的影响

在不同链路负载和突变背景流场景下，探测包数目M和组数P对可用带宽精度的影响，如图5～7所示.

图5　不同P对均方差的影响Figure 5 Impact of P on mean square error

4.1.1M固定，P变化时的均方差

从图5中可以看出：不管当前的链路负载情况如何，当M固定时，均方差曲线随着P的增长总体呈下降趋势，因此增加分组数能提高可用带宽的精度.

4.1.2P固定，M变化时的均方差

由图6可见，不管当前的链路负载情况如何，当P固定时，均方差曲线随着M的增长总体呈下降趋势，这是由于随着M的增长，时间间隔拉长，所得可用带宽的精度更高.

图6　不同M对均方差的影响Figure 6 Impact of M on mean square error

4.1.3几组不同的（P，M）下可用带宽

本文假设P在区间［1，5］，M在区间［16，100］，从图5和6可看出M在［30，40］，P在［4，5］后变化趋于平缓，于是选取M=34和BART中设置的M=17，测量P=2，3，4时的可用带宽，所得结果如图7所示.

比较图7中的（a）和（b）可看出：当M取小值时，增大P会降低可用带宽的精度.然而，只要选择一个稍大的M及合适的P，就能获得较好的测量精度.实验结果表明：当M=34，P=3时，测得的可用带宽的精度最高.

4.2Q对可用带宽精度的影响

根据第3.4节所述，Q中λ是可调节的.令M=34，P=3，测量结果如图8所示.

图7　不同P、M情况下可用带宽的精度对比Figure 7 Accuracy comparison of available bandwidth about diferent P，M

图8　Q对可用带宽精度的影响Figure 8 Impact of Q on accuracy of available bandwidth

图8表明：调整Q对可用带宽精度的影响较小.由于本机制的探测包列中每组使用不同的探测速率，加大了网络利用率的变化，因此不调整Q对可用带宽测量精度的影响不大，使得网络负载和测量时间降低.

4.3在突发背景流下，本机制与BART对比

使用BART中设置的参数M=17，取P=2，测量结果如图9所示.

图9　本机制与BART的测量精度对比Figure 9 Comparison between the accuracy of our mechanism and BART

实验表明：本文提出的机制在突发背景流的网络环境下，测量精度高于BART.当M=17，P=2时，使用BART测得的可用带宽的均方差为0.01，而使用本文所提出的机制测得的均方差为0.007.如果将参数设置成M=34，P=3，那么将获得更高精度的可用带宽，此时均方差为0.005.

5　结语

本文利用探测包列在端到端路径上的单向时延测得网络利用率，该方法无需假设瓶颈容量已知，且探测速率允许低于可用带宽，从而减少了对网络正常流量的影响.构造由P个部分组成的探测包列，为每个部分的探测包设置不同的探测速率，单独计算每个部分探测包在端到端路径上的利用率u（r），因此测量精度无需依赖于Q，同时测量时间和网络负载均大大降低.分析网络利用率与探测速率之间的非线性关系，引入扩展卡尔曼滤波降低突发背景流对测量结果的影响.考虑高速网络环境下出现的丢包现象，用邻居节点代替当前丢失节点的u（r）.因此，该机制能实时、快速、精确地获得高速网络环境下的可用带宽，具有良好的性能.

［1］KIM J C，LEE Y.An end-to-end measurement and monitoring technique for the bottleneck link capacity and its available bandwidth［J］.Computer Networks，2014，58（14）：158-179.

［2］H'AGA P，DIRICZI K，VATTAY G，CSABAI I.Understanding packet pair separation beyond the fuid model：the key role of trafc granularity［C］//International Conference on Computer Communications，2006.

［3］GUERRERO C D，LABRADOR M A.Traceband：a fast，low overhead and accurate tool for available bandwidth estimation and monitoring［J］.Computer Networks，2010，54（6）：977-990.［4］GUERRERO C D，LABRADOR M A.A hidden Markov model approach to available bandwidth estimation and monitoring［C］//Orlando：Proceedings of the Internet Network Management Workshop，2008.

［5］GUERRERO C D，MORILLO D S.On the reduction of the available bandwidth estimation error through clustering with K-means［C］//INFOCOM Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies，Italy，2013.

［6］HU Z，ZHANG D，ZHU A，CHEN Z，ZHOU H.SLDRT：a measurement technique for available bandwidth on multi-hop path with bursty cross trafc［J］.Computer Networks，2012，56（14）：3247-3260.

［7］赵卫虎，孟相如，麻海圆，庄绪春.一种自适应的高精度可用带宽测量算法［J］.计算机测量与控制，2011，19（6）：1297-1300. ZHAO W H，MENG X R，MA H Y，ZHUANG X C.An adaptive method of accurate available bandwith measurement［J］.Computer Measurement&Control，2011，19（6）：1297-1300.（in Chinese）

［8］HU N，LI L E，MAO Z M，STEENKISTE P，WANG J.Locating Internet bottlenecks：algorithms，measurements，and implications［C］//ACM Special Interest Group on Data Communication，New York，2004.

［9］BERGFELDT E，EKELIN S，KARLSSON J M.Real-time available-bandwidth estimation using fltering and change detection［J］.Computer Networks，2009，34（4）：41-54.

［10］LAO L，DOVROLIS C，SANADIDI M Y.The probe gap model can underestimate the available bandwidth of multihop paths［C］//Special Interest Group on Data Communication，Italy，2006.

［11］LI M，WU Y L，CHANG C R.Available bandwidth estimation for the network paths with multiple tight links and bursty trafc［J］.Journal of Network and Computer Applications，2013，36（1）：353-367.

［12］JAIN M，DOVROLIS C.Ten fallacies and pitfalls on end-to-end available bandwidth estimation［C］//New York：Proceedings of the 4th ACM SIGCOMM Conference on Internet measurement，2004.

［13］刘敏，李忠诚，过晓冰.端到端的可用带宽测量方法［J］.软件学报，2006，17（1）：108-116. LIU M，LI Z C，GUO X B.An end-to-end available bandwith estimation methodology［J］. Journal of Software，2006，17（1）：108-116.（in Chinese）

［14］NILSSON M.Measuring available path capacity using short probe trains［C］//in INFOCOM Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies，New York，2010.

［15］NGUYEN U C，TRAN D T，NGUYEN G V.A taxonomy of applying flter techniques to improve the available bandwith estimations［C］//Proceedings of the 8th International Conference on Ubiquitous Internation Management and Communication ACM，New York，2014.

（编辑：王雪）

Accurate and Low Overhead Mechanism for Measuring Available Bandwidth

ZHOU Yi-qiu1，CHEN Bing1，QIAN Hong-yan1，LÜ Zong-lei2
1.College of Computer Science and Technology，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China 2.Information Technology Research Base of Civil Aviation Administration of China，Civil Aviation University of China，Tianjin 300300，China

The available end-to-end bandwidth is an important specifcation in network measurement.Most tools need to spend much time in measuring and analyzing before calculating the available bandwidth.This paper proposes a low overhead mechanism for accurate and fast measurement of the available bandwidth by analyzing the cross trafc efect in the Internet.A model is established to refect the relationship between utilization and the sending rate of probe packets，which is combined with an extended Kalman flter to obtain the new available bandwidth.This mechanism does not require any prior knowledge of the bottleneck link capacity and can reduce the efect of accuracy.Besides，the sending rate of probing packets can be much lower than the available bandwidth.Performance of the mechanism is verifed numerically，showing fast response to burst cross trafc，low estimation error，and short convergence time.

available bandwidth，burst cross trafc，extend Kalman flter

TN911.2

0255-8297（2015）02-0155-12

10.3969/j.issn.0255-8297.2015.02.005

2014-10-16；

2014-12-03

中国民航信息技术科研基地开放课题基金（No.CAAC-ITRB-201301）资助

陈兵，教授，博导，研究方向：计算机网络，E-mail：cb_china@qq.com