微博网络消息传播的ISSR模型

陆静，余小清，万旺根

1.上海大学通信与信息工程学院，上海200444 2.上海大学智慧城市研究院，上海200444 3.上海电力学院电子与信息工程学院，上海200090

微博网络消息传播的ISSR模型

陆静1,2,3，余小清1,2，万旺根1,2

1.上海大学通信与信息工程学院，上海200444 2.上海大学智慧城市研究院，上海200444 3.上海电力学院电子与信息工程学院，上海200090

将微博用户划分为无知者、传播者和拒绝者3种类型，结合微博网络消息传播实际情况，在经典传染病易感染-感染-治愈模型基础上，提出新的无知-传播-传播-拒绝模型.详细描述了传播机制，并对模型的均场方程进行稳态分析.由爬取到的上海典型大学新浪微博用户信息，构建符合真实网络统计性质的网络演化模型，并进行网络动力学分析.仿真结果表明，较大的转发率α和较小的拒绝率δ可以提高微博消息的传播范围，多次转发率γ对传播节点密度也有一定的影响.

微博网络；消息传播；ISSR模型；均场方程；网络演化

微博（microblog）作为一个信息交流平台，每一位注册用户都将拥有双重身份，既可以作为观众，在微博上浏览自己感兴趣的信息；又可以作为发布者，在微博上发布内容供别人浏览；还可以对自己喜欢的用户进行关注，成为后者的粉丝.之后，用户便能在自己的微博首页上浏览关注者更新的微博.在由“关注”和“粉丝”组成的微博网络中，“关注”的人越多，获取的信息就越多，“粉丝”越多，发表的微博就会被越多人看到.某用户发布消息以后，该用户的粉丝（甲乙丙丁...）都可以实时接收信息.如果粉丝中有人（例如甲用户）对该条微博感兴趣，他可以“一键”转发，并以“//@用户名”的形式保留转发路径，这条信息会立即同步出现在甲的微博首页中，同时甲的粉丝（ABCD...）也能实时接收信息，以此类推，实现微博消息的裂变式极速传播.微博使信息传播更加实时，传播内容更加简洁，对新闻和舆论传播产生了革命性的影响.鉴于微博在消息传播的重要地位，研究微博消息的传播与控制方法具有很强的现实意义.

近年来，随着微博网络的流行，学者们纷纷将其列入研究课题，并在网络的静态特性分析方面取得了一些成果，如著名微博服务twitter的网络属性与网络结构测量［1］.文献［2］通过社会热点事件分析新浪微博的用户行为分析，发现带有图片的微博消息具有较高的转发率.文献［3］通过twitter中文本消息的自然语言处理，预测H1N1流感的发展趋势等，但对微博网络动态传播机制的研究并不是很多.实际上，微博消息传播属社会物理学范畴［4］，微博传播的动力学行为与传染病传播有着很大的相似性.文献［5-6］尝试使用传染病模型模拟微博消息的传播过程.同时，在经典传染病模型（susceptible-infectious-removed，SIR）基础上，物理学家们不断创新，提出了免疫者有可能再次成为易感者（susceptible-infectious-removedsusceptible，SIRS）模型［7-8］，在社区行走的个体有可能携带潜伏病毒（susceptible-exposedinfectious-removed-susceptible，SEIRS）的模型［9-10］，考虑了遗忘和提醒机制的（susceptibleinfectious-hibernating-removed，SIHR）模型［11］以及附加隔离措施的（susceptible-infectiousquarantined-recovered-susceptible，SIQRS）模型［12-13］.传染病传播机制与微博传播机制有着很多不同点，如两者的初始条件不同，一条微博的推出通常仅涉及到一个个体，而传染病初始感染人数往往大于1.另外，由于微博更新速度很快，可以达到实时，因而不适合将传染病模型中的遗忘、潜伏机制运用到微博传播中去.本文在借鉴传染病传播模型基础上，必须寻求合理的微博消息传播机制.

为解决上述问题，本文在微博消息传播过程中，考虑了以下切实存在的两大因素：一是某些用户浏览微博后，不充当传播者，不再转发；二是某些用户出于某种原因会重复转发同一条微博，设计了全新的微博传播模型（ignorants spreaders spreaders rejecters，ISSR）.首先对实际爬取到的新浪微博用户关系网络进行统计分析，验证微博网络是否具有“小世界效应”，然后详细介绍ISSR模型的传播机制、均场方程及其稳态分析，最后在构建的小世界网络中进行微博消息传播的计算机仿真，并进一步分析各参数对传播过程的影响.

1　微博用户关系网络的统计性质

从统计物理学的角度看，网络是包含了大量个体以及个体之间相互作用的系统.从数学的角度看，网络可以抽象为由点集V和边集E组成的图G=（V，E）.E中每条边都有V中一对点与之相对应.在微博用户关系网络中，每个节点代表一个微博注册用户，节点之间的关注关系构成网络中的有向边.

1.1出度与入度

度（degree）是单独节点的重要概念.节点i的度ki定义为与该节点连接的其他节点的数目.在有向网络中，节点的度又分为出度（out-degree）和入度（in-degree）.在微博用户关系网络中，节点的出度表示该节点的关注数目，入度表示该节点的粉丝数目.网络中所有节点i的度ki的平均值称为网络的平均度，记为＜k＞.

1.2平均路径长度

假设网络由N个节点组成，第i个节点到第j个节点的距离dij定义为从节点i到节点j的最短路径的边的数目，网络的平均路径长度L则是所有节点对之间距离的平均值，即

1.3集聚系数

假设网络中的一个节点i通过ki条边与其他节点相连，这ki个节点就称为节点i的邻居，它们之间最多存在ki（ki-1）/2条边，则实际存在的边数Ei和总的可能边数ki（ki-1）/2之比就定义为节点的集聚系数Ci，即

1.4实证分析

本文选择国内最大的微博平台–新浪微博作为研究对象，利用调查问卷和新浪微博的开放（application programming interface，API）接口，爬取上海3所典型大学（复旦大学、上海大学、上海外国语大学）的新浪微博用户，并对其构成的局域微博用户关系网络进行统计分析，所得结果如表1所示.可以看出，微博用户关系网络既不是完全规则的，也不是完全随机的，其具有较短的平均路径长度和较大的集聚系数，显现出“小世界效应”.

表1　3所大学的网络参数Table 1 Network parameters of three universities

2　经典传染病模型SIR

在SIR模型中，个体分为3种类型：1）易感者（susceptible），表示未染病但有可能被该类疾病传染的人；2）感染者（infectious），表示已被感染成为病人而且具有传染能力的人；3）免疫者（removed），表示已经康复或者不能传染他人的人.其状态转移过程如下：易感状态→感染状态→免疫状态.感染个体为传染的源头，它通过一定的概率α将疾病传染给易感个体.易感个体一旦被感染，就会成为新的感染源，同时感染个体又以一定的概率β成为免疫个体.免疫个体是指不再参与传播的个体，这种状态的个体不会再对疾病的传播起任何影响.SIR模型适合腮腺炎、麻疹等流行病，患者感染一次就会有抗体，在治愈后可获得终身免疫力.

3　微博消息传播模型ISSR

3.1ISSR模型的传播机制

假设网络中有N个节点，每个节点代表一个微博注册用户.根据微博网络中用户使用微博的习惯，将微博网络中的用户划分为无知节点I（ignorants）、传播节点S（spreaders）和拒绝节点R（rejecters）.无知者是指那些不知道消息，即没有浏览到微博消息的人；传播者是指发布微博消息的人，或看到了微博消息并进行转发，使得消息继续传播的人；拒绝者是指知道消息但却失去传播兴趣的人，即浏览了微博消息，但并没有转发的人，于是可将传播者与拒绝者统一称为浏览者.初始条件下所有节点都处于无知状态，即I态，在某一时刻突然有一个节点发布了一条微博消息，则其变为S态.按照图1所示的模型，这条消息将在微博网络中传播，直到网络中没有传播节点S为止，此时的状态称为终态.

图1　ISSR传播模型Figure 1 ISSR propagation model

传播机制分析如下：

①当传播节点发布消息以后，其粉丝都可以实时

当传播节点发布微博消息以后，其粉丝可以实时接收该条消息.当粉丝浏览了该条微博消息以后，对此条消息感兴趣，希望将其与别人分享，就会充当传播者转发此微博消息.这一过程可以理解为无知节点遇到了传播节点，无知节点以概率α成为了一名传播者.

②粉丝在浏览了其关注者发布的微博消息以后，对消息本身不感兴趣，就会充当拒绝者不转发此微博消息.这一过程可以理解为无知节点遇到了传播节点，无知节点以概率δ成为了拒绝节点.另外，粉丝有可能没有及时登录微博账户，有错过微博消息的可能，故α+δ 61.

③用户发布或转发微博后，可以在自己的微博首页上查看该条微博的阅读数、转发数及评论数.考虑到该用户的众粉丝有可能选择“仅浏览，不转发”的行为，一般而言，阅读数＞＞转发数+评论数.若阅读数非零，即意味着该条微博消息被浏览过，则该用户认为该消息失去了继续传播的价值，有可能失去继续传播该消息的兴趣而使该节点成为拒绝节点.这一过程可以理解为传播节点在发布或转发了一条消息后，遇到了浏览者（包括传播节点和拒绝节点），该传播节点以概率β成为拒绝节点.

④考虑到用户发布微博的心理，某些情况下，用户发布或转发完微博消息后，出于知识、技术、网络新产品的扩散等市场营销策略，或是自身忘记已经转发过，或是对政府官方微博的信任，网民乐于传播这些正确信息，多次转发会增加记忆，往往会多次转发同样的一条微博消息.这一过程可以理解为传播节点自身以概率γ再次成为传播节点.

由于微博用户关系网络呈现“小世界”特征，为便于研究，本文针对ISSR模型提出了两条假设：①在微博消息生命周期内，网络总用户数N不变.②微博网络中用户节点的度服从泊松分布，并令t时刻微博网络中处于无知状态、传播状态和拒绝状态的个体密度分别为I（t）、S（t）和R（t），且

基于节点度分布服从泊松分布的假设，每个节点的度近似等于网络的平均度，即k≈hki.

结合上述传播机制①和②，当无知节点I所关注的用户发布了一条微博以后，该节点浏览了该消息（此过程理解为无知节点与传播节点交互过程），按照自己的兴趣，分别以概率α、δ选择转发或是拒绝转发该条微博的操作，继而转变成为传播节点S或拒绝节点R.当网络中不同状态的个体充分混合时，根据平均场理论可以将对应的均场方程写成

与之相似，由上述传播机制①、③和④可得到方程（5）；由传播机制②和③可得到方程（6）.

初始时刻，微博网络中仅有一人发布了消息，故ISSR模型的初始条件如下：

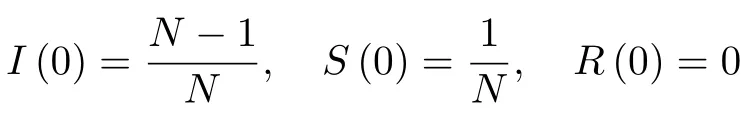
3.2稳态分析

某条微博消息在网络中不再传播时的状态称为系统的稳态.稳态时，微博网络中各类型节点密度将不再随时间变化，且网络中只有无知节点和拒绝节点存在，传播节点的数目为0，即s（∞）=0.因而，在微博消息传播过程中，微博消息自身的影响力可以通过计算网络中最终有多少人浏览了此条微博来衡量.令，接下来讨论R的取值.由式（3）、式（4）、式（6）可以得到

即

可以看出，R=0是方程的一个解.下面研究其非平凡解.令y=1-R-e-ηR，显然，当y=0时可解得其中的一个解为R=0.又因为y0=ηe-ηR-1，y00=-η2e-ηR＜0，故y函数是一凸函数，如图2所示.观察到y0（0）=η-1＞0，且y（1）=-e-η＜0，根据函数的单调性理论可知，y=0的另一个非平凡解为0＜R＜1.并且可以看出，只要满足α/β＞0，就有η＞1，因此无阈值要求便可得到方程的非平凡解.这一结论与传染病SIR模型在均匀网络中的传播情况是截然不同的［7］.

图2　函数y=1-R-e-ηR的形状Figure 2 Form of function y=1-R-e-ηR

4　仿真结果分析

根据爬取到的上海3所典型大学新浪微博用户信息，用随机化重连的方法构建WS小世界网络，网络节点N取5 000，平均度＜k＞取14，任意选择网络中的一个用户作为传播节点，按照ISSR模型的传播规则，令α=0.4，β=0.2，δ=0.1，γ=0.5，可以得到图3所示的3类节点密度变化情况.

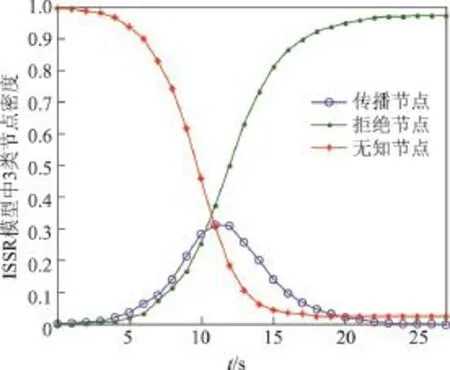
图3　ISSR模型中3类节点密度随时间的变化情况Figure 3 Variation of three kinds of nodes density with time in ISSR model

由图3可以看出，在整个微博消息传播过程中，传播节点的密度随着时间的推移先增长到一个峰值后，再逐渐下降至0，此时网络达到稳态.拒绝节点的密度持续增长且在传播起始阶段变化缓慢，到达稳态后拒绝节点密度不再变化.无知节点的密度变化则呈持续下降的趋势.

γ是指传播节点自身由于忘记或出于某种营销的目的而选择多次转发同一条微博的概率.图4给出了在其他3个参数α=0.4，β=0.2，δ=0.1保持不变的情况下，当γ=0.8，γ= 0.5及γ=0.1时，传播节点密度随时间变化的情况如图4所示.图4中3条曲线总体趋势一致，均为“山峰”形，曲线上升至顶端后下降至0，但γ值越大，峰值也越大，到达稳态所需的时间也越久.由此可以看出，若想利用微博进行广告营销，可以适当增加微博消息的多重转发率，从而提高微博消息的传播密度，加大转发次数，延长传播时间.

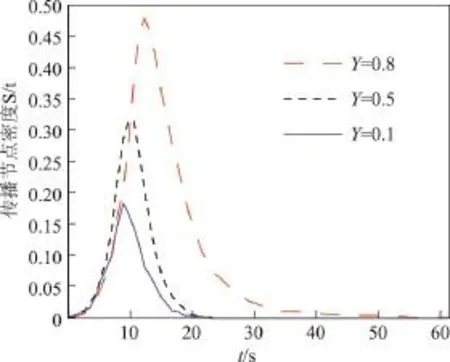
图4　不同γ值时的传播节点密度S（t）Figure 4 Density of spreaders under diferent rate γ

α是指用户浏览了微博消息并进行转发的概率.图5给出了在β、δ、γ 3个参数β=0.2，δ= 0.1，γ=0.1保持不变的情况下，当α=0.5、α=0.4及α=0.3时，免疫节点密度随时间变化情况如图5所示.稳态时的免疫节点密度值可以反映微博消息被用户浏览情况.从图5中可以看出，α越大，R（∞）越大，说明网络中浏览到该条微博消息的人数越多，故传播规模越大.同时，α越大，网络达到稳态的时间越短，说明较大的α值可以起到在较短时间内达到较广传播范围的效果.现实中，微博用户一般对“突发重大事件”、“娱乐新闻”、“互动性话题”等非常感兴趣，往往会选择转发，从而使这些微博消息起到了很好的传播作用.

图5　不同α值时的拒绝节点密度R（t）Figure 5 Density of rejecters under diferent rate α

δ指用户浏览了微博消息但拒绝转发的概率，图6给出了在α、β、γ 3个参数α=0.2，β= 0.3，γ=0.5保持不变的情况下，当δ=0.4，δ=0.3及δ=0.1时，微博网络中拒绝节点密度R（t）变化情况如图6所示.可以看出，δ越大，稳态时的拒绝节点密度越小，如δ=0.4时，R（∞）=0.74，意味着网络中有74%的微博用户将浏览到此条微博消息.相反，δ越小，稳态时的拒绝节点密度越大，到达稳态时间也越短.如δ=0.1时，R（∞）=0.94，意味着网络中有94%的用户将会在较短时间内浏览到消息.因此，对于微博谣言传播而言，如果微博用户能提高识别力度，加大拒绝概率，则会有效控制微博谣言的传播范围.

图6　不同δ值时的拒绝节点密度R（t）Figure 6 Density of rejecters under diferent rate δ

最后，将ISSR传播模型用于复旦大学微博用户网络，任意选择ID号为“1677974197”，昵称为“复旦管院孙一民”的用户作为原创微博用户，得出网络中3类节点密度随时间的变化情况如图7所示，在传播过程中，最大传播节点密度达到了50%，稳态时拒绝节点密度为78%，而无知节点密度为22%.同时可以看出，在相同模型参数条件下（α=0.4，β=0.2，δ=0.1，γ= 0.5），图7与3相类似，反映出复旦大学微博用户网络与人造小世界网络具有相同的传播特征.

图7　复旦大学微博网络3类节点密度随时间的变化情况Figure 7 Variation of three kinds of nodes density with time in the microblog network of Fudan University

5　结语

本文提出的微博网络消息传播模型ISSR综合考虑了微博用户使用微博的习惯及实际转发情形，能很好地模拟真实网络.仿真结果表明，较大的转发率α和较小的拒绝率δ都可以起到在较短时间内达到较广传播范围的作用；多次转发率γ越大，微博消息的传播密度越大，传播时间亦越长.因此，可以通过调整参数的方法来控制不同微博内容的传播，如谣言传播可以加大拒绝概率，微博广告营销可以适当增加微博消息的多重转发率，突发重大事件可以提高转发率扩散事情影响力等.

［1］TEUTLE A R M.Twitter：network properties analysis［C］//Electronics，Communications and Computer（CONIELE COMP），20th International Conference on IEEE，2010：180-186.

［2］GUAN W Q，GAO H Y，YANG M M.Analyzing user behavior of the micro-blogging Website Sina Weibo during hot social events［J］.Physica A：Statistical Mechanics and Its Applications，2014（395）：340-351.

［3］ACHREKAR H，GANDHE A，LAZARUS R.Predicting fu trends using twitter data［C］//Proceedings of IEEE Conference on Computer Communications Workshops，Shanghai，China，2011：702-707.

［4］程洁，张建玮，狄增如.漫谈社会物理学［J］.物理，2010，39（2）：101-107. CHENG J，ZHANG J W，DI Z R.An introduction to sociophysics［J］.Physics，2010，39（2）：101-107.（in Chinese）

［5］ABDULLAH S，WU X.An epidemic model for news spreading on twitter［C］//Proceedings of the 23rd IEEE International Conference on Tools with Artifcial Intelligence（ICTAI），Boca Raton，FL，USA，2011：163-169.

［6］郑蕾，李生红.基于微博网络的信息传播模型［J］.通信技术，2012，45（2）：39-41. ZHENG L，LI S H.A novel information difusion model bassed on microblog network［J］.Communications Technology，2012，45（2）：39-41.（in Chinese）

［7］ENATSU Y，NAKATA Y，MUROYA Y.Lyapunov functional techniques for the global stability analysis of a delayed SIRS epidemic model［J］.Nonlinear Analysis：Real World Applications，2012，13（5）：2120-2133.

［8］LI C H，TSAI C C，YANG S Y.Analysis of epide mic spreading of an SIRS model in complex heterogeneous networks［J］.Communications in Nonlinear Science and Numerical Simulation，2014，19（4）：1042-1054.

［9］WITBOOI P J.Stability of an SEIR epidemic model with independent stochastic perturbations［J］.Physica A：Statistical Mechanics and its Applications，2013，392（20）：4928-4936.

［10］DENPHEDTNONG A，CHINVIRIYASIT S，CHINVIRIYASIT W.On the dynamics of SEIRS epidemic model with transport-related infection［J］.Mathematical Biosciences，2013，245（2）：188-205.

［11］ZHAO L J，WANG J J.SIHR rumor spreading model in social networks［J］.Physica A，2012，（391）：2444-2453.

［12］LIU X N，CHEN X P，TAKEUCHI Y.Dynamics of an SIQS epidemic model with transport-related infection and exit–entry screenings［J］.Journal of Theoretical Biology，2011，285（1）：25-35.

［13］LI T，WANG Y M，GUAN Z H.Spreading dynamics of a SIQRS epidemic model on scale-free networks［J］.Communications in Nonlinear Science and Numerical Simulation，2014，19（3）：686-692.

（编辑：王雪）

ISSR Model of Message Propagation in Microblog Networks

LU Jing1,2,3，YU Xiao-qing1,2，WAN Wang-gen1,2
1.School of Communication and Information Engineering，Shanghai University，Shanghai 200072，China 2.Institute of Smart City，Shanghai University，Shanghai 200444，China 3.School of Electronics and Information Engineering，Shanghai University of Electric Power，Shanghai 200444，China

We divide microblog users into three types：uninformed，forwarder and rejecter，and propose an uninformed-spreader-spreader-rejecter（ISSR）model based on the real situation of message propagation in a microblog network and the classical epidemic model susceptible-infectious-removed（SIR）.The transmission mechanism is described in detail.We also give a steady-state analysis of the mean-feld equations of the model.The network evolution model corresponding to the statistical property of real networks is built based on the crawled information from Sina microblog users in Shanghai's typical universities.Dynamics of the networks is analyzed.Simulation results show a larger retweeting rate α and a smaller rejecting rate δ may improve the spreading range of the microblog message.Meanwhile，the multiple retweeting rate γ has a certain infuence on the densityof spreaders.

microblog network，message propagation，ISSR model，mean-feld equations，network evolution

TP393

0255-8297（2015）02-0194-09

10.3969/j.issn.0255-8297.2015.02.009

2014-01-21；

2014-09-30

国家自然科学基金（No.61373084）；国家“863”高技术研究发展计划基金（No.2013AA01A603）；上海市教育委员会科研创新项目基金（No.14YZ011）资助

陆静，博士生，研究方向：WEB数据挖掘，E-mail：lujingshiep@163.com；万旺根，教授，博导，研究方向：大数据分析，E-mail：wanwg@staf.shu.edu.cn