一般样条滤波器及其在表面计量中的应用
朴伟英 袁怡宝 林海军 许景波
1.哈尔滨理工大学,哈尔滨,150080 2.哈尔滨工业大学,哈尔滨,150001
一般样条滤波器及其在表面计量中的应用
朴伟英1袁怡宝2林海军1许景波1
1.哈尔滨理工大学,哈尔滨,1500802.哈尔滨工业大学,哈尔滨,150001
提出了样条滤波器的一般化表达式,由该表达式可以构造线性样条滤波器、稳健样条滤波和一般样条滤波器。一般样条滤波器保留了部分线性样条滤波器的特性,又具有稳健性。采用Tucky估计,分别采用一般样条滤波器、线性样条滤波器与稳健样条滤波器在表面计量中进行了对比实验,实验结果表明:当表面存在明显的深谷和尖峰时,采用稳健样条滤波器更为合适;当表面近似服从正态分布时,三种滤波器得到的表面粗糙度参数比较接近。
表面计量;样条滤波器;稳健性;滤波中线
0 引言
在表面计量中,表面滤波中线的获取是一个非常关键的问题, 众多参数的计算均与之相关。
ISO11562和ISO16610-1规定用高斯滤波器获取表面滤波中线[1-2]。高斯滤波器存在比较明显的边缘效应,为消除边缘效应的影响,通常需要将原始轮廓首尾一定长度内的数据在滤波后舍弃,这会损失一部分有效测量数据。由于特殊的加工工艺,某些表面可能存在一些深谷和尖峰,高斯滤波器不具有稳健性,高斯滤波中线会在深谷和尖峰附近发生扭曲,不能正确反映表面形貌,导致表面参数不可靠。ISO13565-3提出用Rk滤波器来抑制深谷的影响[3]。Rk滤波器进行两次高斯滤波,第一次滤波后将中线以下的点用中线替代,然后对修改后的轮廓数据进行第二次高斯滤波,获取最终的中线。Rk滤波器能在一定程度上抑制深谷的影响,但不足以克服较大深谷的影响,而且Rk滤波器对尖峰无效。
为解决上述问题,众多学者展开了研究。Krystek[4-5]将三次样条函数与变分方法相结合,构造出三次线性样条滤波器(linear spline filter),并通过遍历搜索的方法来求解分段样条系数以获得最终的中线,滤波器采用自然边界条件,在很大程度上抑制了边缘效应。Goto等[6]将稳健估计理论引入样条滤波器,构造了稳健样条滤波器(robust spline filter)。稳健样条滤波器是一种非线性滤波器,能够抑制尖峰和深谷对滤波中线的影响。
表面滤波器直接决定了滤波中线的形成,而滤波中线对粗糙度参数的评定有重要影响。目前多种滤波器均被应用于表面计量[7],准确理解不同滤波器之间的关系有助于正确评定表面形貌。Zeng等[8]提出了泛化样条滤波器,试图将线性和非线性的稳健样条滤波器统一在一个理论框架下。本文将线性样条滤波器和稳健样条滤波器相结合,提出了样条滤波器的一般表达式,由该表达式可以构造一系列一般样条滤波器(general spline filter),一般样条滤波器既保留了线性样条滤波器的部分特性,又具有稳健样条滤波器的特性。线性样条滤波器和稳健样条滤波器可以解释为一般样条滤波器的两个特例。推导了一般样条滤波器的滤波方程,分别采用一般样条滤波器、线性样条滤波器和稳健样条滤波器在表面计量中进行了滤波实验,并比较了由三种滤波器得到的常用的表面粗糙度参数的异同。
1 样条滤波器的一般化表达式
线性样条滤波器可以用以下最小化问题描述:
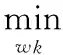
(1)
其中,zk代表未滤波轮廓数据;wk代表滤波中线;数据μ为拉格朗日参数(Lagrange parameter)。式(1)等号右边第一项代表滤波中线对数据的最小二乘拟合,第二项代表样条曲线的弯曲能量。μ就是控制样条曲线拟合程度和弯曲程度的折中参数,与样条滤波器的截止波长密切相关。
最小二乘拟合不具有稳健性,滤波中线会受到深谷和尖峰这些异常信号的影响而发生扭曲,为此Goto等[6]提出了稳健样条滤波器,其定义如下:
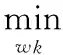
(2)
其中,δk为权。
稳健样条滤波器的前一项为滤波中线对数据的加权最小二乘拟合,因此,稳健样条滤波器可以抑制深谷等异常信号的影响,从稳健估计理论的角度来看,式(2)可以改写为
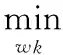
(3)
其中,ρ(v)为稳健估计中M估计的ρ函数,v为自变量,函数ρ(v)前的系数2是为了平衡拉格朗日参数,以保证当μ相同时,稳健样条滤波器与线性样条滤波器具有相同的截止波长。函数ρ(v)与权函数δ(v)存在以下关系:

(4)
式中,ψ(v)为影响函数。
由式(1)和式(3),可以构造以下表达式:
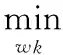
(5)
上式称为样条滤波器的一般表达式,0≤γ≤1,当γ=1时,式(5)就是稳健样条滤波器;当γ=0时,式(5)为线性样条滤波器;当γ取其他值时,式(5)介于稳健样条滤波器和线性样条滤波器之间,可以称为一般样条滤波器。参数γ控制一般样条滤波器的稳健程度,γ越接近1,一般样条滤波器越接近稳健样条滤波器,稳健性越强;γ越接近0,一般样条滤波器越接近线性样条滤波器,稳健性越弱。
2 一般样条滤波器的求解
求解式(5)可以得到滤波方程:
[(1-γ)I+γδ(z-w)+μQ]w=
[(1-γ)I+γδ(z-w)]z
(6)
其中,I为单位矩阵,z、w为n维行向量,δ(z-w)为n×n维矩阵。δ(z-w)取值如下:
δ(z-w)=diag(δ0,δ1,…,δn-1)
(7)
δk=δ(zk-wk)
Q为n×n维系数矩阵。对于开轮廓,有

(8)
在表面计量中,要求在给定的截止波长处,滤波器的幅度传输特性为50%,据此可以得到μ值:
(9)
式(6)为一个稳健估计(robust estimation)问题,从利于计算机编程处理角度考虑,可以用选权迭代法(iteration method with variable weights)求解, 则式(6)可以改写为
[(1-γ)I+γδ(m)(z-w(m))+μQ]w(m+1)=
[(1-γ)I+γδ(m)(z-w(m))]z
(10)
其中,m代表迭代次数,m=0,1,2,…。当γ=0,m=0时,式(10)变为
(I+μQ)w(1)=z
(11)
式(11)是线性样条滤波方程,由式(11)可以得到线性样条滤波中线数据w(1)。w(1)可以作为式(10)的初值,代入式(10)迭代计算,直到满足条件max|w(m+1)-w(m)|≤ε|w(m)|时,迭代结束,ε代表一个很小的数。具体计算过程如下:①首先令式(10)中的γ=0,得到式(11);②求解式(11),得到w的第一次估值;③选取其他γ值;④由z-w得到残差,更新权函数δ;⑤再求解式(10),不断迭代计算步骤④、⑤,直到前后两次解的差值符合要求为止。
3 实验
针对不同的工程表面,采用Tucky估计,比较线性样条滤波器(γ=0)、稳健样条滤波器(γ=1)与一般样条滤波器(γ=0.5)的滤波中线数据。样条滤波方程采用矩阵分解算法,计算程序使用MATLAB编写。为了更准确地评价滤波中线对粗糙度轮廓的影响,分别计算由三种滤波中线得到的表面粗糙度参数Ra,Rq,Rsk,Rku,Rt,RSm,各参数取3位有效数字。为了消除边缘效应的影响,首尾各半个取样长度的数据在滤波后舍弃,不用于粗糙度参数的计算。
图1所示为汽车发动机曲轴表面的滤波实验结果,滤波器截止波长为0.8 mm。该表面的加工工艺为磨削后抛光,表面上存在许多深谷和尖峰。由实验结果可以看出,稳健样条滤波器能很好地抑制深谷和尖峰等异常信号的影响,稳健地获取滤波中线。线性样条滤波器受深谷和尖峰的影响,滤波中线偏离名义轮廓;一般样条滤波器的滤波中线介于线性样条滤波器和稳健样条滤波器中线之间,也存在偏离名义轮廓的现象。

图1 抛光表面线性样条滤波器、一般样条滤波器和稳健样条滤波器的滤波中线比较
图1表面的表面粗糙度参数见表1。可以看出,三者的表面粗糙度参数呈现出明显的规律性。Ra逐渐减小,Rq、Rsk、Rt逐渐增大,显示出粗糙度轮廓与滤波中线的高度相关性。由稳健样条滤波器得到的RSm与另外两者明显不同,说明对于存在深谷和尖峰的轮廓,滤波中线的变化会引起RSm的明显变化。Rq的物理意义与Ra类似,均表示表面的粗糙程度。在该例中,Ra更为准确地反映了表面的粗糙程度,而Rq却与Ra呈现负相关的特性。这说明对于含有深谷和尖峰的轮廓,Rq不能正确反映表面形貌。Rsk、Rku分别代表表面的偏斜度和峭度,由于Rsk、Rku的计算过程也要使用Rq,故这两个参数的准确性也存在疑问。

表1 抛光表面的粗糙度参数
图2所示为磨削加工表面的滤波实验结果,滤波器截止波长为0.8 mm。该表面的幅度概率密度分布具有近似正态分布的特征,由实验结果可以看出,稳健样条滤波中线仍然最平坦,线性样条滤波中线弯曲程度最大,一般样条滤波中线介于两者之间。
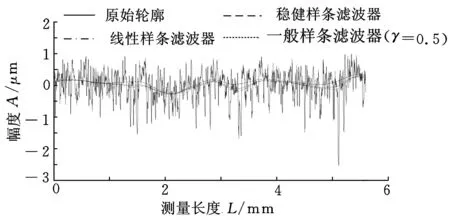
图2 磨削表面线性样条滤波器、一般样条滤波器和稳健样条滤波器的滤波中线比较
图2表面的粗糙度参数见表2,粗糙度轮廓是由原始轮廓减去滤波中线后得到的,三者滤波中线不同,粗糙度轮廓自然也不同,而三者的Ra几乎相同,这说明Ra对表面轮廓的变化不敏感。RSm的差距也很小,说明对于近似服从正态分布的轮廓,滤波中线的微小变化对RSm的影响很小。Rq、Rsk、Rku、Rt则逐渐增大,根据实验结果,一般来说,滤波中线越平坦,Rq越大。

表2 磨削表面的粗糙度参数
在实验中还选取了其他γ值,结果表明一般样条滤波中线始终介于线性样条滤波中线和稳健样条滤波中线之间,一般来说,随着γ的增大,迭代次数增加,计算量也相应增加,滤波器的稳健性增强,滤波中线也越接近稳健样条滤波中线,反之结果则相反。
由不同的一般样条滤波器可以得到不同的一般样条滤波中线,相应可以得到不同的表面粗糙度轮廓和粗糙度参数。实验结果表明,Ra较为可靠,但Ra对表面粗糙度轮廓的变化不敏感,只有当轮廓出现较为明显变化时,Ra才能有所反映。Rq与Ra呈现不同的变化规律,特别是对于不服从正态分布的表面,Rq与实际情况出入较大,因此,Rq不够可靠,不能用来单独表征表面粗糙度。Rsk、Rku、RSm、Rt等参数有一定的参考意义,但这些参数一般不能单独使用。
4 结语
本文提出了样条滤波器的一般化表达式,该表达式不仅建立了线性样条滤波器与稳健样条滤波器的关系,而且根据该表达式可以构造滤波器,选取不同的γ值可以得到稳健性不同的一般样条滤波器。在表面计量中进行了应用实验,实验结果表明,当表面存在明显的深谷和尖峰时,采用稳健样条滤波器更为合适;当表面近似服从正态分布,不存在明显的离群点时,三种滤波器得到的表面粗糙度参数比较接近。
[1]International Standard Organization .ISO 11562:1996.Geometrical Product Specifications(GPS)-Surface Texture: Profile Method-Metrological Characteristics of Phase Correct Filters[S].1996.
[2]International Standard Organization.ISO/TS 16610-211.Geometrical Product Specifications(GPS)-Filtration-Part 21:Linear Profile Filters:Gaussian Filters[S].2011.
[3]ISO 13565-1.Geometrical Product Specification(GPS)-Surface Texture:Profile Method Surfaces Having Stratified Functional Properties.Part 1.Filtering and General Measurement Conditions[S].1996.
[4]Krystek M.Form Filtering by Splines[J].Measurement,1996,18(1):9-15.
[5]Krystek M.Discrete L-spline Filtering in Roundness Measurements[J].Measurement,1996,18(2):129-138.
[6]Goto T,Miyakura J, Umeda K. A Robust Spline Filter on the Basis of L2-Norm[J]. Precision Engineering, 2005, 29(2):157-161.
[7]Raja J,Muralikrishnan B,Fu Shengyu.Recent Advances in Separation of Roughness,Waviness and Form[J].Precision Engineering,2002,26(2):222-235.
[8]Zeng W,Jiang X,Scott P.A Generalised Linear and Nonlinear Spline Filter[J].Wear,2011,271(3/4):544-547.
(编辑陈勇)
A General Spline Filter and Its Applications in Surface Metrology
Park Weiying1Yuan Yibao2Lin Haijun1Xu Jingbo1
1.Harbin University of Science and Technology,Harbin,150080 2.Harbin Institute of Techniology,Harbin,150001
A general expression of spline filter was proposed and the linear spline filter,robust spline filter and general spline filter could be derived from this expression.The general spline filter kept the characteristics of the linear spline filter partly,and had the characteristics of robustness.Using Tucky estimation,all of the three kinds of spline filter were compared in surface metrology.The experimental results show that the rubost spline filter is more suitable while there are some deep valleys and high peaks in the surface;the roughness parameters of all spline filters are close while the surface approximately fits normal distribution.
surface metrology;spline filter;robustness;reference line
2015-01-28
国家自然科学基金资助项目(61179024);黑龙江省基金资助项目(12541152)
TB921DOI:10.3969/j.issn.1004-132X.2015.20.006
朴伟英,男,1976年生。哈尔滨理工大学测控技术与通信工程学院讲师、博士。主要研究方向为滤波方法。袁怡宝,男,1964年生。哈尔滨工业大学电气工程与自动化学院教授、博士。林海军,男,1967年生。哈尔滨理工大学测控技术与通信工程学院教授、博士。许景波,男,1973年生。哈尔滨理工大学测控技术与通信工程学院教授、博士。
——书写要点(三)

