闭环双驱动混合输出六自由度并联机构运动分析

陈宇航　赵铁石　耿明超　苑飞虎　李二伟

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,066004　 2.燕山大学先进锻压成形技术与科学教育部重点实验室,秦皇岛,066004

闭环双驱动混合输出六自由度并联机构运动分析

陈宇航1,2赵铁石1,2耿明超1,2苑飞虎1,2李二伟1,2

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,066004 2.燕山大学先进锻压成形技术与科学教育部重点实验室,秦皇岛,066004

提出一种分支含闭环双驱动单元、可实现混合输出的六自由度并联机构。分析了动平台混合运动时驱动分支的等效形式，以及独立位姿运动和振动时驱动分支的等效形式;分析了混合运动关于位姿运动输入和振动输入的位置反解，对振动输入的位置反解设计了基于机构运动特点的逐次逼近法；运用螺旋理论求得动平台混合运动时关于全体12个独立广义坐标的一、二阶影响系数，得到从广义输入到动平台旋量速度、加速度的线性映射；通过数值算例分别对位姿运动输入和振动输入的理论分析结果进行了验证,算例仿真表明,提出的两种双驱动输入分配计算规则均能得到确定的混合运动输出。

并联机构;闭环双驱动;旋量;混合输出

0　引言

大范围位姿运动与不同频率振动相叠加的混合运动广泛存在于工程应用领域的实际工况，例如卫星等航天器上的并联精确指向平台与隔振平台[1]、多维动力学环境模拟实验系统等。采用单一驱动器在同一机构中实现这两种不同性质运动的混合输出对驱动器要求极高，且容易损坏驱动器。双重驱动并联机构能将位姿运动输入与振动输入分离，根据运动性质选择对应的驱动器,通过分支传动，转化为动平台的混合输出。

双重驱动的概念最早出现在宏/微双重驱动机器人系统中[2-3],一般由宏动和微动两部分组成，微动部分附着于宏动部分之上使系统整体频带宽度增加，以实现机器人大工作空间与高精度定位。国内外学者在宏/微双重驱动领域做了大量研究工作[4-6]。文献[7]设计了一种用于染色体解剖的宏/微双重驱动机器人,宏动部分采用6-PPPS机构，微动部分为6-PSS机构;文献[8]对FAST宏/微双重驱动机构进行实时运动规划,实现了末端执行器精确轨迹跟踪的目标。

双重驱动并联机构和一般的宏/微双重驱动机构有所不同,它是在并联机构的每个驱动分支中增加一个驱动副,使机构自由度变为原来的2倍，但输出自由度不变。如果这两个驱动分别采用宏动与微动量级驱动器，则称为宏/微双重驱动并联机构。文献[9]采用压电驱动器与柔性铰链设计了一种3-PUPU宏/微双重驱动并联机构,该机构可进行微米级的位置调节并有较好的振动抑制效果;文献[10]分别采用压电电机和压电陶瓷作为宏动与微动驱动，机构采用6-PUPU形式，达到厘米级的工作空间和纳米级的定位精度；文献[11-13]在Stewart平台的P副上串联宏/微两重驱动(可理解为一种6-UPPS机构)，通过振动主动控制使各自由度上的扰动显著衰减；文献[14]提出了4-PSPS/PRPUR五自由度宏/微双重驱动并联载物台定位机构；文献[15-17]分别对四自由度、五自由度双重驱动并联机构进行型综合，丰富了双重驱动并联机构构型。将宏/微双驱动的概念拓展，双重驱动并联机构可应用于更多需要两种不同性质运动混合输出的工况。上述各机构，双重驱动连接于同一串联运动链，增加了运动链长度，且二级驱动一般不与机架相连，增大了一级驱动的负载，降低了机构动力学性能。

本文设计一种分支带闭环双驱动单元的，可实现位姿运动与振动混合输出的六自由度并联机构。双驱动单元中两驱动器均连接于基座，降低了驱动分支惯量，提高了机构的动特性。机构将位姿运动与振动的输入分离，合理分配双驱动输入量，可得到指定的混合输出。

1　机构特征与双驱动分支等效形式

1.1闭环双驱动并联机构特征

机构由动平台、基座及6条结构相同的双驱动分支构成,分支以两两一组的形式沿圆周均布于基座上。驱动分支为(PRRPR)US机构,其中(PRRPR)为闭环双驱动单元,以两个P副作为驱动输入，靠外侧的驱动为第一驱动，靠内侧的驱动为第二驱动。第一驱动下端通过R副与基座铰接于点ei(i=1,2,…,6),第二驱动沿竖直方向,设其轴线与基座交点为fi，所有ei和fi在同一水平面内。分支上端通过S副与动平台铰接于点bi。机构三维造型如图1所示。

动平台的位姿运动输出由第一驱动实现，振动输出由第二驱动实现。通过双驱动不同形式输入组合，可实现动平台位姿运动与振动的混合输出。

1.2双驱动分支等效形式

分支中含(PRRPR)双驱动的闭环机构,可应用约束螺旋理论将其转化成等效广义运动副[18]。

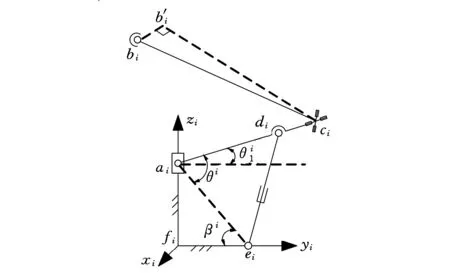
图2　分支机构简图

将图2中闭环机构视为具有两个分支的并联机构，fiai为第一分支,eidi为第二分支。其中分支fiai的运动螺旋为

(1)

根据$∘$r=0[18]得分支fiai约束螺旋系：

(2)

同理,分支eidi的运动螺旋系为

(3)

坐标变量中没有上标i的表示常量,数值在各{i}系中相同。分支eidi约束螺旋系为

(4)

由式(2)、式(4)得闭环机构的约束螺旋系为

(5)

则闭环单元的运动螺旋为

(6)

注意到式(5)、式(6)数值上分别与式(2)、式(1)相同，由式(6)可知，闭环双驱动单元等效为由一个移动副P和一个转动副R组成的复合运动副。分支i等效为[PR]US支链,对动平台没有约束作用。机构杆件数n=20,运动副数g=24,由修正的Grübler-Kutzbach公式计算机构自由度为12,6条双驱动分支刚好提供12个输入,保证机构有确定的运动输出。

动平台混合运动由位姿运动和振动组成，根据两种运动的幅值分别求对应驱动量。分析任一驱动时，另一驱动视为锁定。单驱动瞬时闭环单元的等效形式如图3所示。

(a)位姿运动　(b)振动图3　闭环双驱动单元瞬时等效形式

图3a所示为实现动平台位姿运动时闭环双驱动单元的等效形式，显然此时可等效为一个R副,分支变为RUS分支;图3b所示为实现动平台振动时闭环双驱动单元的等效形式。式(4)变为

(7)

由式(2)、式(7)得闭环单元的约束螺旋系为

(8)

求式(8)的反螺旋，得闭环单元运动螺旋为

(9)

可知闭环单元仍可等效为一个R副。

2　机构混合输出位置反解

机构位置反解是实现运动控制的基础。任一瞬时，动平台的混合运动可分解为位姿运动和振动两部分。

2.1位姿运动位置反解

以ei和fi所在平面中心为原点,建立参考坐标系oxyz,记为{o}系,x轴与f1f2平行,z轴竖直向上;以bi所在圆的圆心为原点建立运动坐标系pxpypzp,记为{p}系,xp轴与b1b2平行,zp轴垂直动平台向上。初始位置时,{p}系与{o}系对应坐标轴平行，如图1所示。

bi在{o}系与{i}系的坐标分别为

(10)

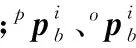
(11)

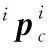
(12)

2.2振动位置反解

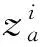
(13)

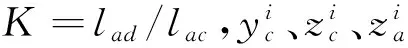
(14)

计算机求解式(14)速度较慢,且多数控制器一般不具有直接求解高次方程的函数，所以该方法不适用于实时伺服运动控制。根据分支机构运动特点，本文设计了一种逐次逼近求解法[19]。

(15)

图4　ci点轨迹关系图

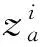
经过测算,该方法效率较高。当精度ε=0.0001 mm时,对于工作空间内的任意位姿,最多循环25次即可得到结果,平均用时0.8 ms，满足实时伺服控制要求。所用计算机相关配置为CPUInteli5-4570 3.2GHz,内存2G。

3　广义坐标到动平台速度和加速度的映射

任意时刻,将动平台混合运动的速度、加速度分解为对应于位姿运动和振动的两部分

(16)

式中,VC、AC为动平台混合运动旋量速度、加速度；VG、AG为动平台位姿运动旋量速度、加速度;VV、AV为动平台振动旋量速度、加速度。

图5　逐次逼近法求解流程

3.1位姿运动速度与加速度

当动平台处于任意位姿(Rip,ip)时,可得分支i各铰链点坐标，分支内各运动副螺旋可以确定，动平台旋量速度对应位姿运动的部分为[20-21]

(17)

由文献[22]中的推导可得

(18)

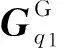
根据闭环输入单元的几何关系，可得等效驱动速度与广义速度的关系:

(19)

将式(19)写成矩阵形式：

(20)

将式(20)代入式(18),得到位姿运动时广义速度向动平台旋量速度的线性映射:

(21)

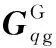
对式(17)求导,并根据文献[22]对Hessian矩阵的推导,得

(22)

由文献[22]得

(23)

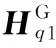
式(19)对时间求导得

(24)

将式(24)写成矩阵形式

(25)

i,j=1,2,…,6

将式(20)、式(25)代入式(23)并整理得位姿运动时广义加速度向动平台旋量加速度的映射:

(26)

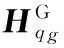
3.2振动速度与加速度

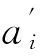
此时等效R副输入速度向动平台振动部分旋量速度的线性映射关系式为

(27)

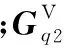
(28)

式(28)对时间求导得

(29)

(a)瞬时等效R副与虚设杆件(b)瞬时等效四杆机构图6　振动驱动闭环单元瞬时等效机构简图

将式(29)写成矩阵形式,有

(30)

将式(30)代入式(27),得振动广义速度向动平台振动旋量速度的线性映射为

(31)

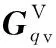
与位姿运动推导相似，动平台振动旋量加速度映射关系为

(32)

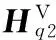
(33)

将式(33)写成矩阵形式得

(34)

将式(30)、式(34)代入式(32)并整理得振动广义坐标向动平台振动旋量加速度的映射为

(35)

3.3混合运动速度与加速度

将式(21)、式(26)、式(31)、式(35)代入式(16)并整理得系统广义坐标与动平台混合运动旋量速度、加速度的映射关系式:

(36)

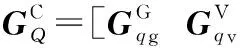
4　数值算例与仿真

给定机构结构参数如下：动平台铰链点所在圆直径950 mm，第一驱动铰链点中心所在圆直径1103.68 mm,第二驱动铰链点中心所在圆直径805.07 mm,lac=460 mm,lbc=751 mm,{p}系相对{o}系的初始高度为700 mm。

4.1位姿运动算例

Ryg=20°sinπt

ωyg=20°πcosπt

εyg=-20°π2sinπt

理论推导所得为动平台旋量速度、旋量加速度与输入的映射关系，所以要将动平台运动转化为旋量形式。通过MATLAB计算得各分支位姿输入的位移、速度和加速度随时间变化曲线如图7所示。图7曲线表明，动平台绕yp轴做±20°大范围位姿运动时，输入的位移、速度和加速度变化平滑，变化范围满足常见的驱动器技术参数指标要求，机构具有良好的运动特性。同时,机构具有以较小输入获得较大输出的特点。动平台在其他自由度方向的位姿运动也有相似的结果，篇幅所限不一一列举。

(a)位姿输入位移

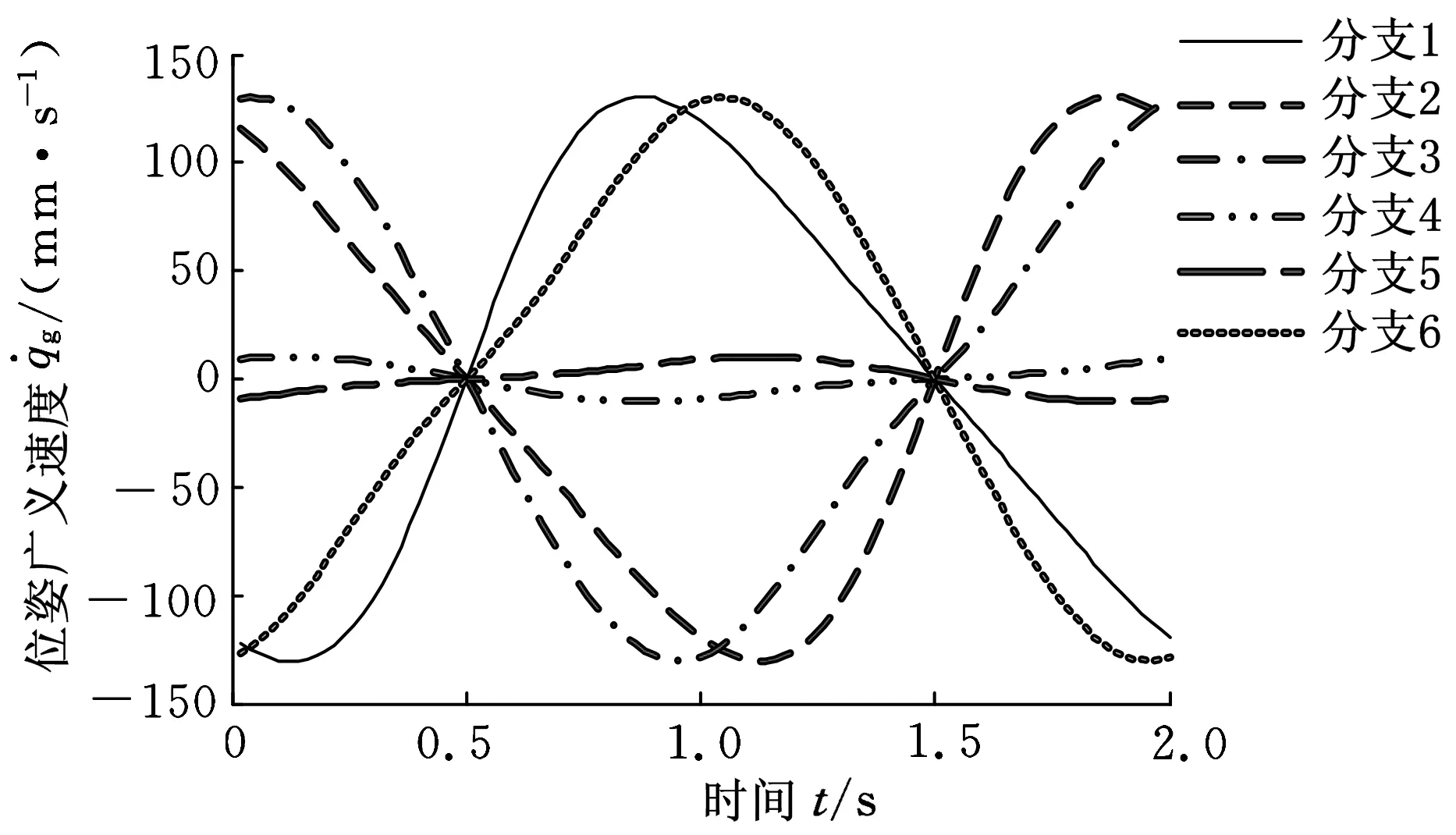
(b)位姿输入速度

(c)位姿输入加速度图7　位姿输入规律

4.2振动算例

运用2.2节设计的逐次逼近法计算振动位置反解,并由式(31)和式(35)计算振动输入速度和加速度，结果如图8所示。当动平台以±10°的振幅和5 Hz振动频率绕yp轴做角振动时,振动输入位移变化范围为64.91 mm,最大速度为963.26 mm/s,最大加速度约为4.5g,在1个振动周期内输入变化较平稳,振动驱动器能够达到这样的指标。在实际应用中，一般不会出现±10°这样大振幅的振动，可见该机构在振动方面应用空间比较广阔。

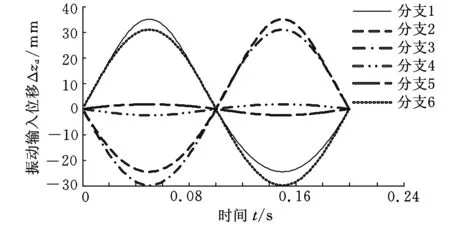
(a)振动输入位移

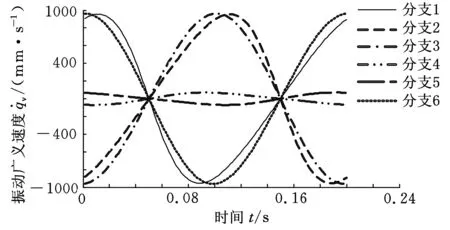
(b)掁动输入速度

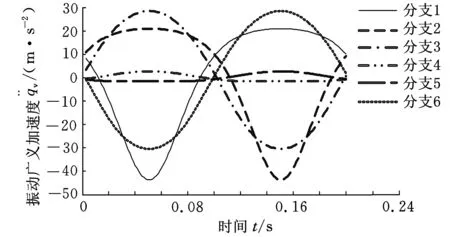
(c)振动输入加速度图8　振动输入规律

4.3混合运动算例仿真

由于机构自由度大于输出自由度,所以对于动平台的任意位姿，输入有无穷多解。为了得到唯一解，需设定求解规则。本文设定两种求解规则，具体如下。

规则1优先计算位姿输入，以每一时刻位姿驱动伸长为结构参数计算对应时刻的振动输入。该规则适用于振动输入频率高于位姿输入频率，且位姿驱动伸长量更容易实时获取的场合。

以动平台绕yp轴转动的混合运动为例，位姿运动、振动和混合运动如下(位姿运动频率0.5 Hz,振动频率5 Hz)：

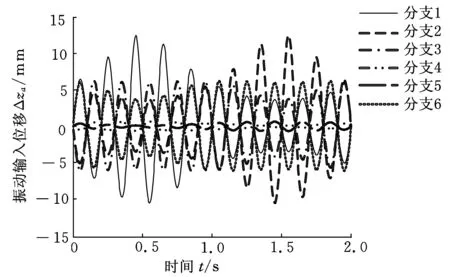
图9　规则1振动输入位移

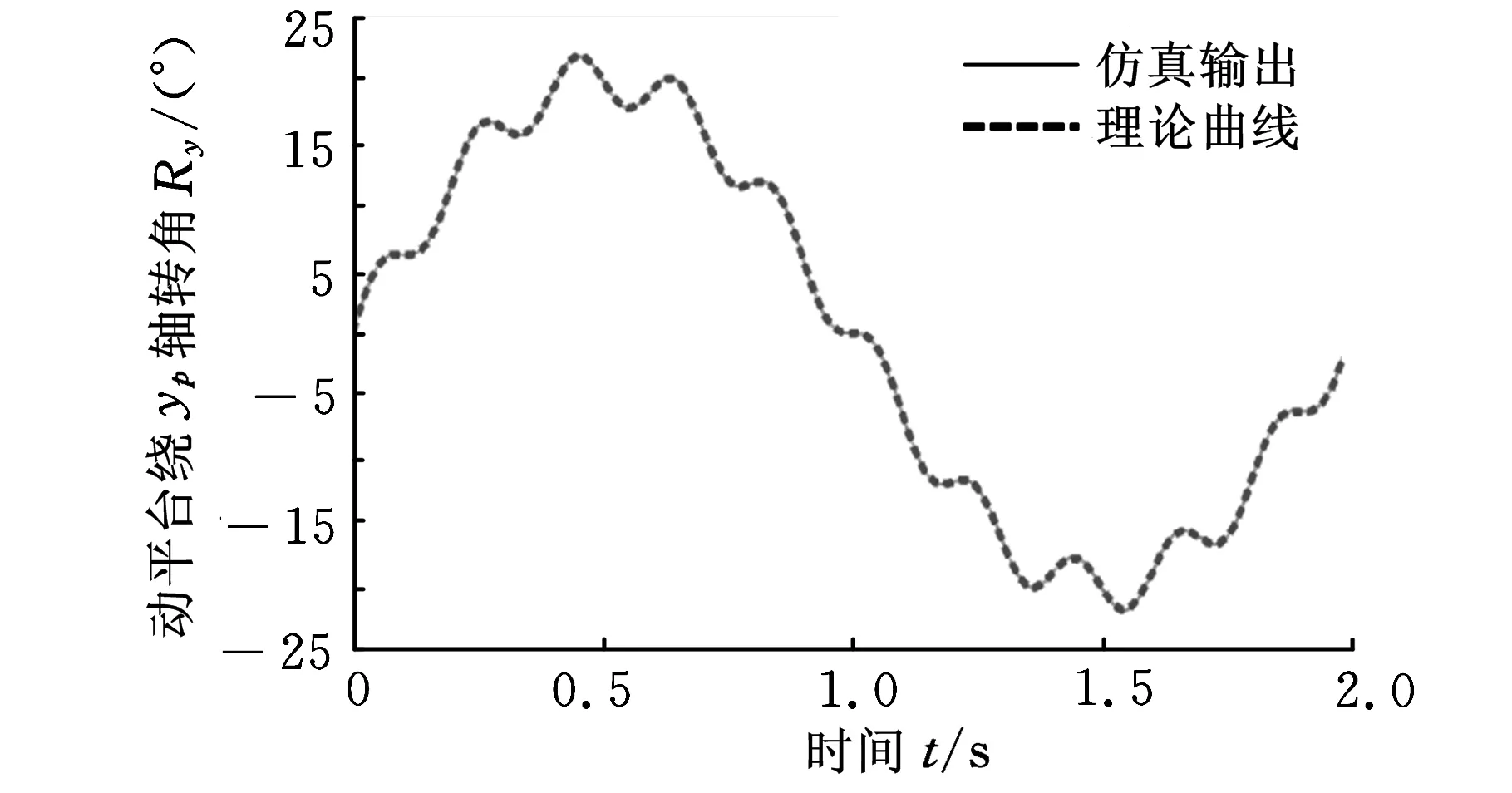
图10　规则1机构混合输出

位姿输入如图7a所示，对应振动输入如图9所示。通过ADAMS仿真得到机构混合运动输出,如图10所示。可见仿真输出曲线与理论曲线几乎完全重合，说明按规则1求解双驱动匹配输入量能够得到指定的混合运动输出。

规则2优先计算振动输入，以每一时刻振动驱动伸长为结构参数，计算对应时刻位姿输入。该规则适用于振动输入频率低于位姿输入频率，且振动驱动伸长量更容易实时获取的场合。

给定动平台绕yp轴转动的运动规律，位姿运动、振动和混合运动分别如下(位姿运动频率0.5 Hz，振动频率0.1 Hz)：

振动输入规律如图11所示，对应的位姿输入规律如图12所示。在ADAMS中,依据所得双驱动输入规律进行仿真，得机构混合运动输出曲线如图13所示。仿真曲线仍与理论曲线重合，证明按规则2求解双驱动输入量同样可以得到确定的混合运动输出。

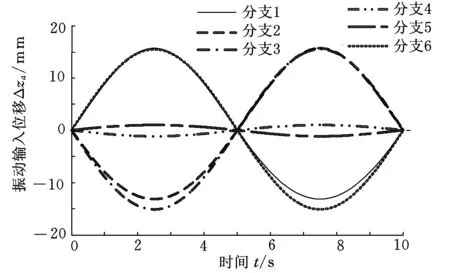
图11　规则2振动输入

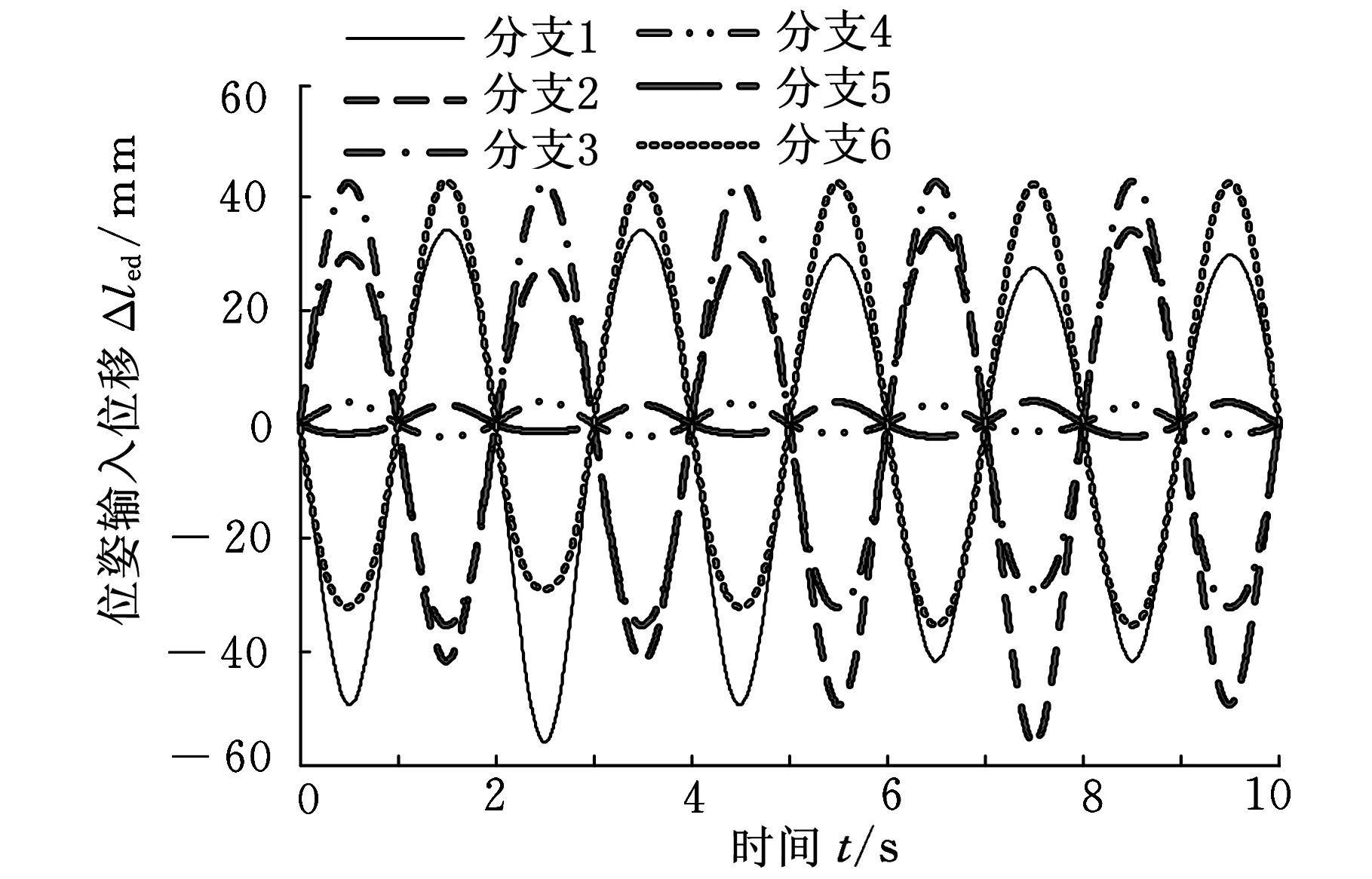
图12　规则2位姿输入

图13　规则2机构混合输出

5　结论

①面向工程应用领域对不同特性运动混合输出的需求，设计了分支带闭环双驱动单元的混合输出六自由度并联机构。②将混合运动分离，运用约束螺旋理论分别得到对应位姿运动与振动的驱动分支等效形式。③得到动平台混合运动关于位姿运动和振动的位置反解关系，针对振动位置反解设计了一种逐次逼近求解法，其计算结果满足求解精度及实时性要求，避免了求解高次方程的复杂过程。④推导出机构关于12个独立广义坐标的一、二阶影响系数，得到广义坐标到动平台混合运动旋量速度、加速度的线性映射。为多输入少输出系统的运动学求解提供参考。⑤数值算例证明，机构在实现独立的位姿输出和振动输出时，驱动特性良好，主要驱动参数满足常规驱动器技术指标；提出两种双驱动输入分配计算规则，仿真表明两种规则均能得到确定的混合运动输出。

[1]杨建中. Stewart并联机器人在航天器上的应用 [C]//全国第十二届空间及运动体控制技术学术会议论文集.北京: 中国空间技术研究院,2006:426-431.

[2]Sharon A,Hogan N,Hardt D E.High Bandwidth Force Regulation and Inertia Reduction Using a Macro/Micro Manipulator System[C]//The 1988 IEEE International Conference on Robotics and Automation.Philadelphia:IEEE,1988:126-132.

[3]孙立宁,董为,杜志江. 宏/微双重驱动机器人系统的研究现状与关键技术[J].中国机械工程,2005,16(1):91-95.

Sun Lining,Dong Wei,Du Zhijiang.State-of-the-Art and Key Technologies of Macro/Micro Dual Manipulator System[J].China Mechanical Engineering,2005,16(1):91-95.

[4]Yang Tangwen,Xu Weiliang,Han Jianda.Dynamic Compensation Control of Flexible Macro-Micro Manipulator Systems[J].IEEE Transactions on Control Systems Technology,2010,18(1):143-151.

[5]Taghirad H D,Nahon M A.Jacobian Analysis of a Macro-micro Parallel Manipulator[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Zurich:IEEE,2007:1-6.

[6]Lew J Y,Trudnowski D J.Vibration Control of a Micro/Macro-manipulator System[J].Control Systems,IEEE,1996,16(1):26-31.

[7]Feng J,Gao F,Zhao X,et al.A New Macro-micro Dual Drive Parallel Robot for Chromosome Dissection[J].Journal of Mechanical Science and Technology,2012,26(1):187-194.

[8]Duan Xuechao,Qiu Yuanying,Du Jingli,et al.Real-time Motion Planning for the Macro-micro Parallel Manipulator System[C]//2011 IEEE International Conference on Robotics and Automation(ICRA).Shanghai:IEEE,2011:4214-4219.

[9]Yuan Yun,Li Yangming.Modeling and Control Analysis of a 3-PUPU Dual Compliant Parallel Manipulator for Micro Positioning and Active Vibration Isolation[J].Journal of Dynamic Systems,Measurement,and Control, 2012,134(2):021001.

[10]Dong Wei,Sun Lining,Du Zhijiang. Design of a Precision Compliant Parallel Positioner Driven by Dual Piezoelectric Actuators[J].Sensors and Actuators A:Physical,2007,135(1):250-256.

[11]李伟鹏,黄海.基于Hexapod的精密跟瞄平台研究[J].宇航学报,2010,31(3):681-686.

Li Weipeng,Huang Hai.Study of Space-born Precise Tracking/Pointing Platform Based on Hexapod[J].Journal of Astronautics,2010,31(3):681-686.

[12]崔龙,黄海.高稳定精密跟瞄机构设计与仿真[J].北京航空航天大学学报,2008,33(12):1462-1465.

Cui Long,Huang Hai.Design and Simulation of Highly Stable and Precise Tracking-pointing Platform[J].Journal of Beijing University of Aeronautics and Astronautics,2008,33(12):1462-1465.

[13]李伟鹏,黄海,边边.精密跟瞄Hexapod平台研制及其振动控制[J].航空学报,2009,30(2):259-264.Li Weipeng,Huang Hai,Bian Bian.Design and Vibration Control of Precision Pointing Hexapod[J].ACTA Aeronautica et Astronautica Sinica,2009,30(2):259-264.

[14]赵铁石,冯海兵,刘艳辉,等.五自由度宏/微双重驱动并联机构及其运动学分析[J].燕山大学学报,2010,34(6):501-507.Zhao Tieshi,Feng Haibing,Liu Yanhui,et al.5-DOF Dual-drive Parallel Mechanism and Its Kinematics[J].Journal of Yanshan University,2010,34(6):501-507.

[15]Li Ningnin,Zhao Tieshi,Bian Hui.Type Synthesis of Dual-driven 4-DOF Parallel Mechanism[J].Machine Design and Research,2008,24(1): 51-53.

[16]范彩霞, 刘宏昭. 双驱动五自由度并联机构型综合[C]//第9届中国机构与机器科学应用国际会议(CCAMMS 2011) 暨中国轻工机械协会科技研讨会论文集. 上海: 中国机械工程学会机械传动分会机构学专业委员会,2011.

[17]范彩霞,刘宏昭.基于李群理论的双驱动2T3R五自由度并联机构型综合[J]. 中国机械工程,2012,17:2053-2057.

Fan Caixia,Liu Hongzhao.Type Synthesis of Dual-driven 2T3R 5-DOF Parallel Mechanism Based on Lie Group Theory[J],China Mechanical Engineering,2012,17:2053-2057.

[18]Huang Zhen，Liu Jingfang,Zeng axing.The General Method of Analysis of Mechanisms Mobility Based on Constraint Screw Theory[J].Science in China: E Series,2009,39(1):84-93.

[19]Zhang Hui,Wang Qiming,Ye Peiqing,et al.Forward Kinematics of General Stewart Platform and the Application[J].Journal of Mechanical Engineering,2002,38(Supp):108-112.

[20]Zhao Tieshi,Geng Mingchao,LiuXiao,et al.Kinematics and Dynamics Hessian Matrixes of Manipulators Based on Lie Bracket[EB/OL].[2013-03-06].http://www.paper.edu.cn/releasepaper/content/201303-167.

[21]耿明超,赵铁石,赵飞等.非惯性系下弹性欠驱动机器人动力学建模及应用[J].中国机械工程,2014,15:2080-2085.

Geng Mingchao,Zhao Tieshi,Zhao Fei,et al.Dynamics Model of Elastic Underacutated Robot in a Non-inertial Frame and Its Applications[J].China Mechanical Engineering,2014,15:2080-2085.

[22]黄真, 赵永生, 赵铁石. 高等空间机构学[M].北京:高等教育出版社,2006.

(编辑苏卫国)

Kinematic Analysis of a 6-DOF Parallel Mechanism with Closed Loop Dual-drive and Composite Output

Chen Yuhang1,2Zhao Tieshi1,2Geng Mingchao1,2Yuan Feihu1,2Li Erwei1,2

1.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System， Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of Education of China,Yanshan University,Qinhuangdao,Hebei,066004

A parallel mechanism that can accomplish 6 dimensional composite output was proposed,each leg of it had a closed-loop dual-drive unit.The equivalent form of one leg was analysed when the moving platform was under composite motion,so as the equivalent form of one leg corresponding to independent position and orientation motion and vibration.The inverse position solution about position and orientation drive and vibration drive were analysed,for inverse position solution of vibration drive,a kind of successive approximation method was designed based on the motional features of mechanism.Using screw theory the first and second order influence coefficients of all the 12 general coordinates were obtained, so the linear mapping from general inputs to screw velocity and acceleration of moving platform was obtained.Theoretical analyses of position and orientation motion drive and vibration drive were verified by numerical examples,it is indicated by the numerical simulation that composite output can accomplish through the two rules presented for dual-drive distribution.

parallel mechanism;closed-loop dual-drive;screw;composite output

2014-10-21

国家自然科学基金资助项目(51375420)

TP24；V19DOI：10.3969/j.issn.1004-132X.2015.20.017

陈宇航,男，1986年生。燕山大学机械工程学院博士研究生。研究方向为并联机器人技术。赵铁石(通信作者),男,1963年生。燕山大学机械工程学院教授、博士研究生导师。耿明超,男,1984年生。燕山大学机械工程学院博士研究生。苑飞虎，男,1986年生。燕山大学机械工程学院博士研究生。李二伟,男,1987年生。燕山大学机械工程学院博士研究生。