基于扩展卡尔曼粒子滤波算法的锂电池SOC估计
赵又群 周晓凤 刘英杰
南京航空航天大学,南京,210016
基于扩展卡尔曼粒子滤波算法的锂电池SOC估计
赵又群周晓凤刘英杰
南京航空航天大学,南京,210016
锂电池荷电状态用来描述电池剩余电量的多少,进而反映电动汽车的续驶里程,是电池管理系统中的核心参数。电池循环次数、瞬间大电流以及温度等因素都会使电池特性发生变化,使用扩展卡尔曼滤波算法对电池荷电状态进行估计,会有较大的误差甚至导致算法不收敛。为了有效地抑制发散以及噪声的影响,基于锂电池混合噪声模型,应用扩展卡尔曼粒子滤波算法对锂电池荷电状态和电流漂移噪声进行同步估计。最后根据充放电试验数据进行仿真分析,结果证明了该算法的优越性。
锂电池;荷电状态;混合噪声模型;扩展卡尔曼粒子滤波
0 引言
电动汽车以环保、节能及轻便等特点被人们所青睐,而作为关键技术部件的电池,其性能直接影响到整车性能的好坏。锂离子电池具有电压高、比能量高、充放电寿命长、无记忆效应、无污染、自放电率低、工作温度范围宽和安全可靠等优点,是目前电动汽车首选的核心动力源[1]。它具有高度的非线性,且受温度、充放电倍率以及容量等因素影响,其动态过程无法用单一的模型来描述。因此,如何利用电池的可测参数来实现当前电池剩余电量准确估计,一直以来是电动汽车电池管理系统的核心问题和急需解决的技术难点,也是一项重要而富有挑战性的任务[2]。只有准确估计荷电状态(SOC)才能起到优化电池性能、提高电池安全性和延长电池使用寿命等作用。
目前,工程上最常用的算法是A·h计量法[3-5],它是一种开环估计方法,简单易实现,但累计误差大,估计精度低。针对误差引起的算法发散问题,文献[6]提出基于电池状态空间模型的卡尔曼滤波算法,实现了电池SOC的闭环估计。文献[7-11]均采用扩展卡尔曼滤波算法对电池SOC进行估计,使得极化效应的影响大大减弱,提高了电池SOC计算的精度。为减小锂电池非线性引起的误差,也有研究人员将粒子滤波算法应用到电池SOC估计中。文献[12]为了较好地解决粒子滤波算法中粒子的退化问题,根据遗传算法的原理,提出了遗传粒子滤波算法并给出其估计电池SOC的实现方法,通过实例验证,并与标准粒子滤波算法进行对比分析,结果显示遗传粒子滤波算法对电池SOC的估计更加准确,精度更高。
电池实际工作过程中,温度、循环次数、瞬间大电流等因素使电池的极化内阻、可使用容量等存在较大差异,在估计电池SOC时往往存在较大误差甚至发散。为抑制系统非线性和发散,单纯地使用粒子滤波算法在粒子数目比较少时可能会出现粒子匮乏的现象,而且算法对模型依赖性强并且存在抖动。因此为了消除算法抖动和粒子退化的现象,本文基于锂电池混合噪声模型,应用扩展卡尔曼粒子滤波(EKPF)算法对锂电池SOC进行估计,并将其与扩展卡尔曼滤波(EKF)算法和粒子滤波(PF)算法进行比较分析。
1 锂电池混合噪声模型
电池SOC是不能直接测量的,必须通过温度、电流、电压等能测量的参数进行估算,因此,建立一个准确的电池模型对精确估算电池SOC十分重要。一个理想的电池模型应该能够较好地反映电池的各种特性,而且阶数不能太高,便于计算,易于工程实现。本文借鉴文献[2]提出的结合Shepherd模型、Unnewehr模型和Nernst模型的复合模型,考虑电流漂移噪声的干扰,建立混合噪声模型,具体数学表达式如下:
K3lnxk+K4ln(1-xk)
(1)
式中,yk为电池工作电压;ireal为真实放电电流;R为电池内阻,本文考虑充放电内阻的不同,充电时R=Rc,ireal为负,放电时R=Rd,ireal为正;K0、K1、K2、K3、K4为模型参数;xk为k时刻的瞬时荷电状态。
为了表征温度、充放电倍率、容量等对电池SOC估计的影响,对SOC作如下定义:
(2)
κ=|i(t)|/CN
式中,δSOC为电池的SOC值;η为充放电效率;T为温度;κ为充放电倍率;CN为常温下电池的标称容量;C(T,κ,t)为在不同温度、不同充放电倍率下的电池可用容量。
为了抑制电流漂移噪声的干扰,将电池荷电状态及电流漂移噪声一起作为状态变量进行同步估计[13]。状态方程中的电流应当是除去电流漂移的电流真实值,即
(3)
放电电流的测量不可避免存在漂移和噪声。将放电电流的测量值i分成两个部分,即电流真实值ireal和电流噪声值is,则
i=ireal+is
(4)
将式(4)代入式(3)得
(5)
将式(5)作离散化处理得
(6)
式中,ik-1为k-1时刻的测量电流,is,k-1为k-1时刻的电流噪声值;Δt为时间间隔。
该混合噪声模型能有效抑制电流漂移的干扰,简单易操作,计算量不大,易于工程实现,而且模型中的参数易于辨识,只要获得N组电流、电压和真实SOC数据,就可以由最小二乘法辨识得到模型参数。
2 模型参数辨识
系统辨识是在已知输入和输出数据的基础上,在某种准则条件下,估计出系统模型的未知参数的。目前常用的辨识方法有最小二乘法、梯度校正法、极大似然法等。最小二乘法由于原理简单、收敛较快、易于理解、易于编程实现等特点,在系统参数估计中应用相当广泛[14]。
对于电动汽车来说,被控对象通常都可以不断提供新的输入输出数据,而且还希望利用这些新的信息来改善估计精度,因此需要在线辨识电池模型的参数。本文采用递推最小二乘法对锂电池复合模型进行参数辨识,递推公式为
(7)
(8)
P(k)=(I-K(k)φT(k))P(k-1)
(9)
递推最小二乘法进行模型参数辨识一般步骤[14]如下:
(2)采样当前输出y(k)和输入u(k);
(4)k→k+1,返回步骤(2),继续循环。
本文对额定电压3.2 V、额定容量20 A·h的锂离子电池的充放电试验数据,采用递推最小二乘法对建立的混合噪声模型进行参数辨识,辨识结果如表1所示。
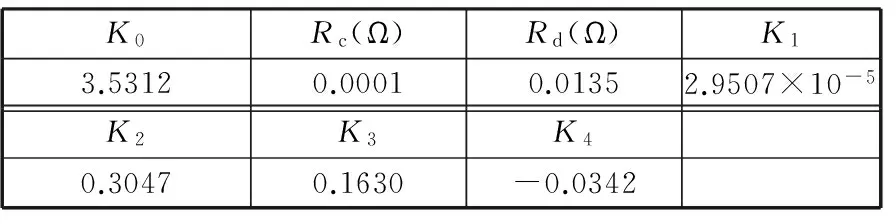
表1 锂离子电池复合模型参数表
3 基于EKPF算法的SOC估计
EKPF算法是解决非线性系统状态变量估计问题最常用的方法,粒子滤波摆脱了解决非线性滤波问题时随机变量必须满足高斯分布的制约条件,能够应用在任意非线性非高斯随机系统中,在许多领域取得了成功应用。粒子滤波器中密度分布的建议值一般决定了粒子滤波器应用的性能。为了避免粒子匮乏和算法抖动,本文以扩展卡尔曼滤波器作为建议分布,实现基于扩展卡尔曼粒子滤波算法对锂电池SOC的估计。
首先建立锂电池的离散状态空间模型。锂电池SOC作为状态变量,负载电压作为观测变量,将上文建立的复合模型的状态空间方程进行离散化。则状态方程:
(10)
观测方程:
K3ln(xk)+K4ln(1-xk)+vk
(11)
其中,wk为系统噪声,vk为观测噪声,它们均为零均值的高斯白噪声,wk~N(0,Q),vk~N(0,R),Δt为离散系统采样周期,模型参数K0、R、K1、K2、K3、K4已由上文第2节的方法辨识得到,其值详见表1。
根据锂离子电池状态空间方程,利用EKPF实现电池SOC估计的算法流程如图1所示。
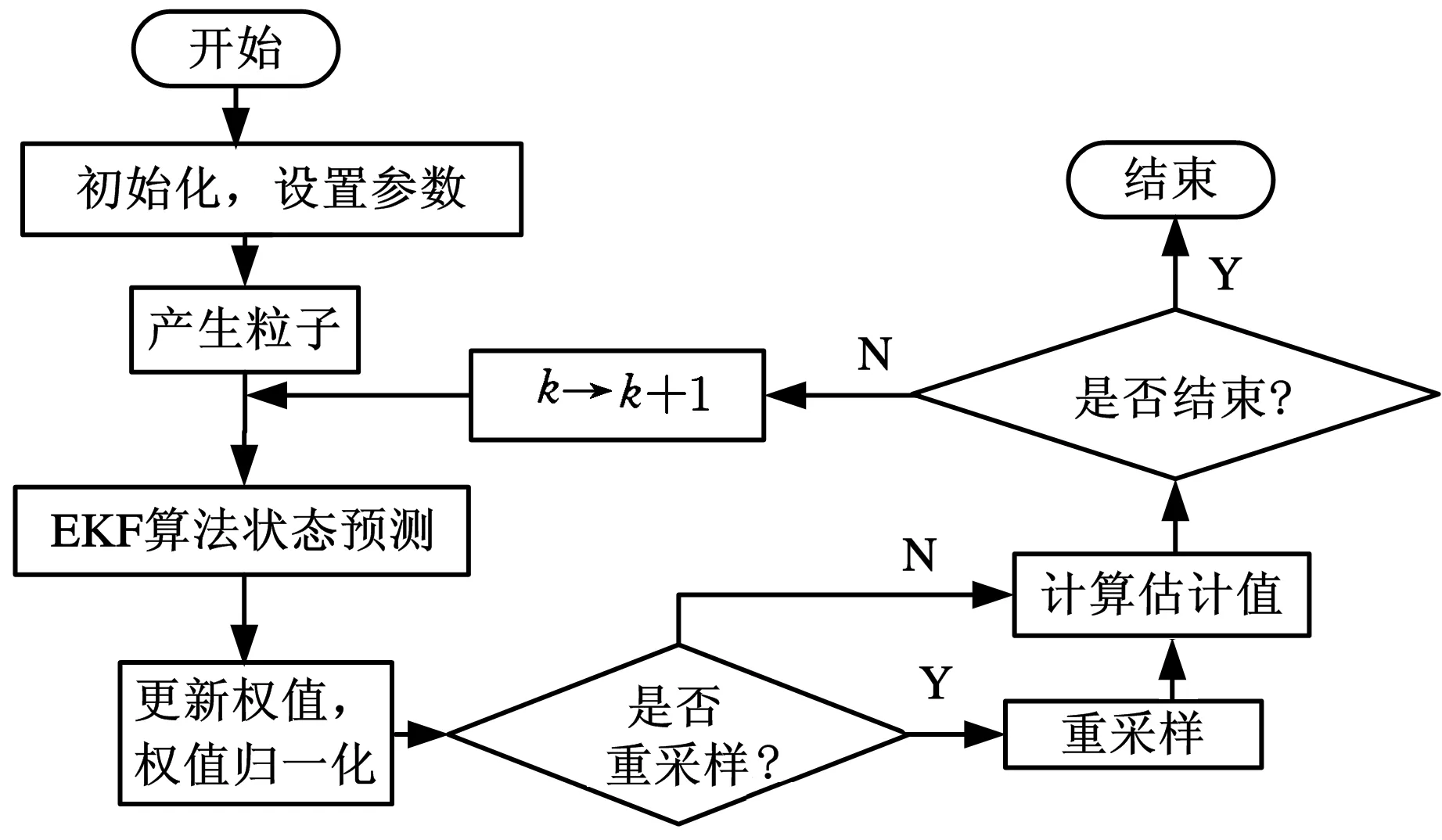
图1 EKPF算法流程图
具体算法步骤如下:

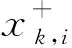
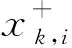
(12)
式中,g(·)为已知电流和荷电状态情况下,由混合噪声模型计算得到的电压值。
然后,进行归一化处理:
(13)
(14)
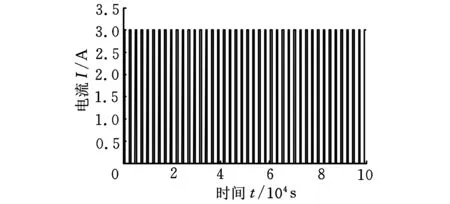
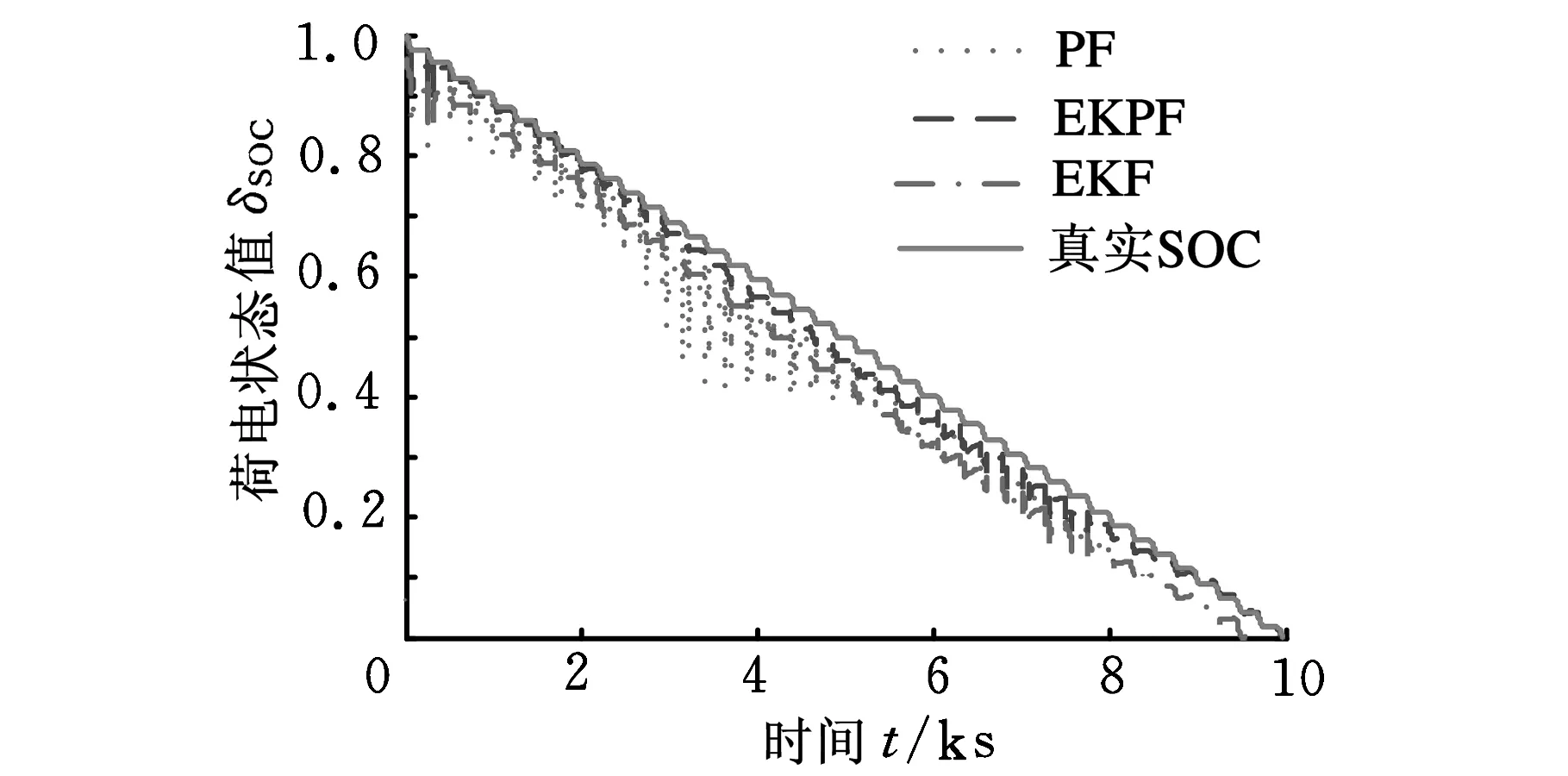
若Ne f f (15) (4)循环迭代k→k+1,转步骤(2)循环迭代。 为了验证EKPF算法对锂电池SOC估计的精确性,对3.2 V/20 A·h的锂电池进行放电试验。首先将电池组充满电(δSOC(0)=1),然后在恒温条件下对电池组放电,放电电流波形如图2所示,整个放电时间为105s,采样间隔Δt为10 s。 图2 放电电流波形 试验中,粒子数N设定为50,系统噪声和观测噪声的方差分别取2×10-14、25×10-6,分别采用EKF、PF和EKPF三种算法对电池SOC进行估计,估计结果图如图3所示。 图3 三种不同算法的SOC估计结果 图3中的真实SOC值是通过放电试验法得到的。对电池进行持续放电,测出在一定的很小的时间间隔后释放的电量,再根据SOC的定义便可计算得到该时刻的真实SOC值。为了定量地比较EKF、PF和EKPF的性能,定义试验的均方根误差为 (16) 为了考察算法的时间复杂度,定义第k次试验算法的耗时时间为tk,则算法的单次平均消耗时间为 (17) 通过计算,EKF、PF和EKPF三种不同电池SOC估计算法的均方根误差和单次平均消耗时间的值如表2所示。 表2 EKF、PF和EKPF估计SOC性能比较 从图3和表2的仿真试验结果可以看出,基于锂电池混合噪声模型的EKPF算法精度较高,既说明了算法的优越性,也表明了模型的准确性。单独使用PF算法时抖动很明显,而EKPF算法则比较平滑,在均方根误差的指标上也优于EKF算法和PF算法,但由于算法复杂,计算量相对较大,故单次平均消耗时间相对较长。 外界温度、循环次数、瞬间大电流等因素的影响,会使电池的极化内阻、可使用容量存在较大差异,在估计电池SOC时往往存在较大误差甚至发散。为抑制电流漂移的干扰、系统非线性、算法发散以及算法本身的抖动,本文基于锂电池混合噪声模型,应用EKPF算法对锂电池SOC进行估计。仿真试验结果表明,EKPF算法能有效地估计锂电池荷电状态。 [1]郭炳焜,徐徽,王先友,等.锂离子电池[M].长沙:中南大学出版社,2002. [2]Cai C H,Du D,Liu Z Y.Battery State-of-charge(SOC) Estimation Using Adaptive Neuro-fuzzy Inference System(ANFIS)[C]//IEEE International Conference on Fuzzy Systems. St. Louis,MO,United States,2003:1068-1073. [3]林成涛,王军平,陈全世,等.用改进的安时计量法估计电动汽车动力电池SOC[J].清华大学学报,2006,46(2):247-251. Lin Chengtao,Wang Junping,Chen Quanshi,et al.Improved Ah Counting Method for State of Charge Estimation of Electric Vehicle Batteries[J].Journal of Tsinghua University(Science and Technology),2006,46(2):247-251. [4]Mark E.Adaptive State of Charge Algorithm for Nickel Metal Hydride Batteries Including Hysteresis Phenomena[J].Journal of Power Source,2004,126(1):236-249. [5]曾洁,卜凡涛.基于多项式回归算法的锂电池SOC估测[J].大连交通大学学报,2011,32(4):70-74. Zeng Jie,Bu FanTao.Study of SOC Estimation and Measurement of Li-Ion Battery Based on Polynomial Regression Algorithm[J].Journal of Dalian Jiaotong University,2011,32(4):70- 74. [6]Plett G L.Extended Kalman Filtering for Battery Management Systems of LiPB-based HEV Battery Packs[J].Journal of Power Sources,2004,134(2):277-292. [7]范波,田晓辉,马建伟.基于EKF的动力锂电池SOC状态预测[J].电源技术,2010,34(8):797-799.Fan Bo,Tian Xiaohui,Ma Jianwei.Ekf-Based Estimation of Lithium-Ion Traction-Battery SOC[J].Chinese Journal of Power Sources,2010,34(8):797-799.[8]夏超英,张术,孙宏涛.基于推广卡尔曼滤波算法的SOC估算策略[J].电源技术,2007,31(5):414-417. Xia Chaoying,Zhang Shu,Sun Hongtao.A Strategy of Estimating State of Charge Based on Extended Kalman Filter[J].Chinese Journal of Power Sources,2007,31(5):414-417. [9]李超,刘忠庆.基于参数与状态联合估算的SOC预测法[J].电源技术,2012,36(3):362-365.Li Chao,Liu Zhongqing. SOC Estimate Based on Joint Determination of Parameters and States[J].Chinese Journal of Power Sources,2012,36(3):362-365.[10]戴海峰,魏学哲,孙泽昌.基于扩展卡尔曼滤波算法的燃料电池车用锂离子动力电池荷电状态估计[J].机械工程学报,2007,43(2):92-95. Dai Haifeng,Wei Xuezhe,Sun Zechang,Estimate State of Charge of Power Lithium-Ion Batteries Used on Fuel Cell Hybrid Vehicle with Method Based on Extended Kalman Filtering[J].Chinese Journal of Mechanical Engineering,2007,143(2):92-95. [11]Liye Wang,Lifang Wang,Chenglin Liao.Research on Improved EKF Algorithm Applied on Estimate EV Battery SOC[C]//2010 Adia-Pacific Power and Engergy Engineering Conference.Chengdu,China,2010:1-4. [12]张洁.基于粒子滤波算法的电动汽车剩余电量动态估计研究[D].北京:北京交通大学,2012. [13]刘新天.电源管理系统设计及参数估计策略研究[D].合肥:中国科学技术大学,2011. [14]庞中华,崔红.系统辨识与自适应控制MATLAB仿真[M].北京:北京航空航天大学出版社,2009. (编辑郭伟) SOC Estimation for Li-Ion Battery Based on Extended Kalman Particle Filter Zhao YouqunZhou XiaofengLiu Yingjie College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing,210016 As the key parameter for power battery management,the SOC of Li-ion battery described the residual capacity,and indicated the remainder driving range of electric vehicles.The cycles,instantaneous high current,abnormal temperatures and other factors would change cell characteristics,which might introduce larger errors even divergence over time if the extended Kalman filter algorithm were applied to the SOC estimation.To suppress the divergence and noise,this paper proposed a method based on EKPF algorithm to realize accurate SOC and the current drift estimation on the Li-ion battery mixed noise model.Finally,the superiority of this method was validated by simulation results. Li-ion battery;state-of-charge(SOC);mixed noise model;extended Kalman particle filter(EKPF) 2013-03-28 2014-07-28 国家高技术研究发展计划(863计划)资助项目(2011AA11A210,2011AA11A220) U463< class="emphasis_italic">DOI :10.3969/j.issn.1004-132X.2015.03.019 赵又群,男,1968年生。南京航空航天大学能源动力学院教授、博士研究生导师。研究方向为车辆系统动力学。发表论文120余篇。周晓凤,女,1988年生。南京航空航天大学能源动力学院车辆工程系硕士研究生。刘英杰,男,1982年生。南京航空航天大学能源动力学院车辆工程系博士研究生。4 仿真试验及结果分析
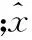

5 结束语

