异种钢焊接接头蠕变过程的有限元模拟

张伯奇　蔡志鹏　李克俭　李轶非　潘际銮

清华大学，北京，100084

异种钢焊接接头蠕变过程的有限元模拟

张伯奇蔡志鹏李克俭李轶非潘际銮

清华大学，北京，100084

异种钢焊接接头常应用于高温下工作的大型构件，其蠕变特性和持久性能对结构的安全性具有重要意义。常规的蠕变试验和高温持久试验仅适用于均匀材料，对非均匀的异种钢接头存在局限性。为了解决该问题，针对某种构件上采用的含有过渡层的马氏体钢与珠光体钢异种金属接头进行了有限元建模。分别利用K-R蠕变损伤模型和改进的θ Projection模型进行模拟计算，并且对比了非均匀结构与均匀的焊缝、过渡层和母材的蠕变特性。对比发现，非均匀结构中抗蠕变性能较弱的过渡层部分的蠕变速率要大于均匀的过渡层材料的蠕变速率，这说明材料的不均匀性会带来附加的蠕变损伤。因此，仅通过均匀材料的蠕变试验来预测非均匀结构的寿命是不可靠的，应采用蠕变试验与有限元计算相结合的方法进行非均匀结构的寿命预测。

异种钢焊接；非均匀材料；蠕变模拟；有限元模拟

0　引言

异种钢焊接目前被广泛应用于核电、火电、石油化工等装备制造领域。异种钢焊接技术可以充分发挥不同材料的优势，降低成本，并提高结构设计的灵活性，是大型装备制造中的关键技术之一[1-2]。

异种钢焊接接头大多工作在高温环境下，其蠕变特性和持久性能对结构的服役安全性至关重要。

对于异种钢焊接接头，常规的蠕变和持久试验存在难以克服的局限性。首先，蠕变和持久试验均是针对均匀材料而设计的，难以反映异种材料之间的相互作用；然后，蠕变和持久试验均采用单轴拉伸的加载方式，而非均匀结构必然存在复杂的多轴应力状态[3-4]，与试验假设并不相符；最后，蠕变和持久试验周期长、成本高，严重制约了整个产品的设计和生产。因此，采用有限元计算方法模拟异种钢接头的蠕变过程并预测其寿命是行之有效的措施。

对耐热钢蠕变过程的模拟已有很多研究。Kachanov[5]提出了经典的K-R蠕变损伤模型;文献[6-7]将K-R蠕变模型推广到多轴应力条件下;刘学等[8]拟合了P91钢的蠕变损伤模型，并进行了多轴应力条件下的有限元计算。还有很多学者从组织劣化方面研究了蠕变损伤模型的物理本质[9]。除了上述对均匀材料蠕变模型的研究以外，还有一些学者对焊接接头非均匀结构的蠕变行为进行了研究。张建强等[4,10]对T91钢和HR3C钢焊接接头的蠕变失效进行了有限元模拟，但只采用了简单的幂律蠕变模型，而未对接头的损伤情况进行表征；Sunil-Goyal等[11]利用有限元方法对2.25Cr1Mo钢热影响区的IV型裂纹进行了预测，同样只采用了幂律蠕变模型，而未反映加速蠕变阶段应力应变的剧烈变化。可见，对焊接接头，特别是对异种钢接头这种复杂的非均匀结构进行蠕变模拟还有待进一步研究。

本文采用K-R蠕变损伤模型和θ Projection模型分别研究含有2.25Cr1Mo过渡层的马氏体钢与珠光体钢焊接接头的蠕变行为，以期探索一种合理的异种钢接头寿命预测方法。

1　异种钢接头结构与蠕变试验

为了解决异种钢母材回火参数的矛盾，本文研究的异种钢接头采用了带有过渡层的结构。首先在马氏体钢母材一侧用埋弧焊堆焊若干层2.25Cr1Mo过渡层，焊后进行(670～690 ℃)×12 h回火，并将过渡层加工成坡口形状。然后用TIG打底焊连接带有过渡层的马氏体钢与珠光体钢，并用2.25Cr1Mo焊丝埋弧焊填充。最后进行(650～660 ℃)×20 h回火。焊接接头的结构如图1所示。图2所示为经过硝酸酒精腐蚀后的焊接接头的照片。焊接接头的母材和焊丝的主要成分见表1。

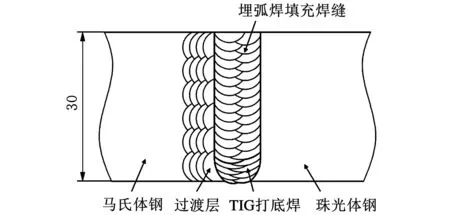
图1　异种钢焊接接头结构示意图

图2　焊接接头照片

为了确定接头持久性能的薄弱环节，对整个接头进行了高温持久试验。分别采用提高温度和增大应力的加速试验方法进行试验，试验温度在500～620 ℃之间，试验应力在80～180 MPa之间。试样横跨接头的各个区域，通过断裂位置即可判断其薄弱部位。试验发现，所有试样均在过渡层内断裂，如图3所示。

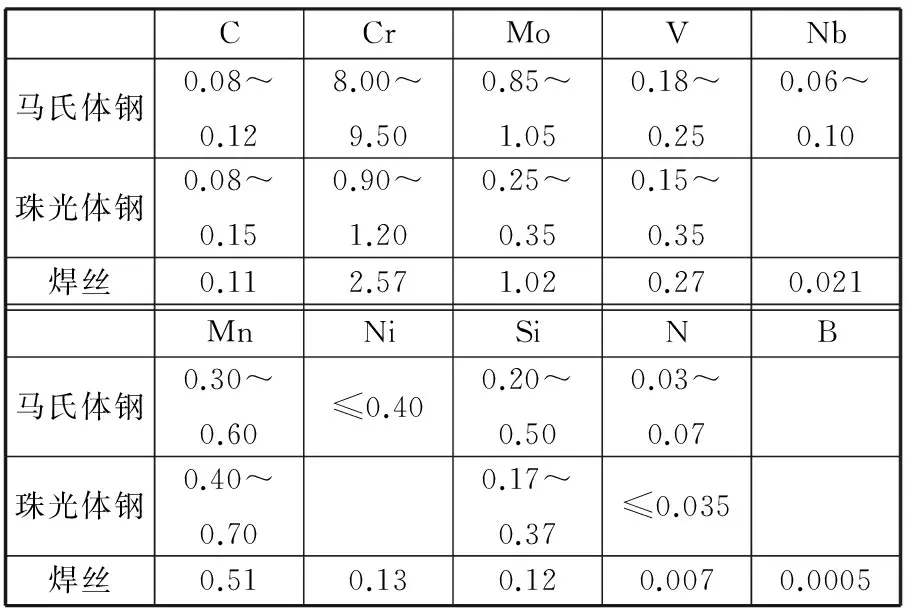
表1　焊接接头各部分的主要成分(质量分数)　%

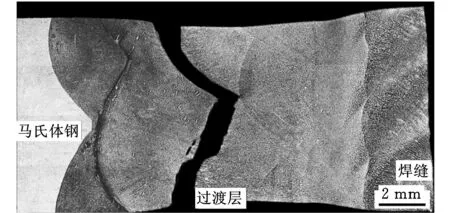
图3　接头高温持久试样金相照片

可见过渡层是接头持久性能的薄弱环节。因此，在有限元计算中着重研究过渡层的蠕变行为，模型包括马氏体钢母材、过渡层和焊缝三部分，而省略了珠光体钢一侧的建模。

过渡层是多层结构，由于对高合金的马氏体钢母材逐层稀释，故各层过渡层的成分有所不同。但是每层过渡层厚度都很小，无法单独制取蠕变试样，只能忽略各过渡层之间在蠕变特性上的差别。过渡层材料的不均匀性将通过弹性模量的差别来体现。

在600 ℃、不同应力下分别对马氏体钢母材、过渡层和焊缝进行蠕变试验，得到其蠕变曲线。蠕变试样直径为10 mm，小于焊缝和过渡层的宽度，试样标距为55 mm。以马氏体钢为例，测得其蠕变速率与时间的关系如图4所示。

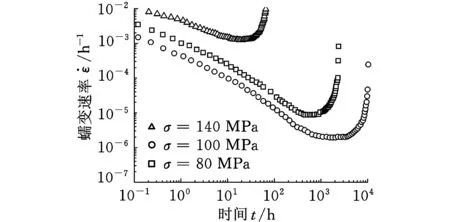
图4　600 ℃下马氏体钢母材的蠕变试验数据

2　蠕变模型的拟合

2.1K-R蠕变损伤模型的拟合

蠕变过程一般分为蠕变硬化、稳态蠕变和加速蠕变3个阶段。其中，前2个阶段可用幂律模型很好地描述，而第3阶段通常采用K-R蠕变损伤模型来描述。

K-R蠕变损伤模型应用广泛，它不仅可以计算加速蠕变过程中构件的应力应变情况，还能预测构件的损伤部位。K-R蠕变损伤模型可用2个方程来表述，即与损伤变量耦合的蠕变速率方程和损伤演化方程，其形式如下：

(1)

(2)

式中，ε为应变；σ为应力；D为损伤变量(初值为0，单调增大，变为1时表示完全损伤)；A、B、n、p、φ为常数，由材料性质决定。

在应力恒定的条件下，对式(2)积分：

(3)

式中，t为时间。

则有

(4)

将式(4)代入式(1)，得

(5)

将蠕变硬化和稳态蠕变阶段的应变率表示为幂律形式，得到完整的应变率方程：

(6)

式中，q、C、m为系数。

利用蠕变试验获得的数据，采用非线性拟合的方法对式(6)进行拟合，分别得到马氏体钢母材、过渡层和焊缝的蠕变模型常数。该蠕变模型可以获得良好的拟合度，以马氏体钢母材在600 ℃、100 MPa下的蠕变速率曲线为例，其拟合情况如图5所示。

图5　采用K-R蠕变损伤模型拟合的马氏体钢蠕变速率曲线

2.2θ Projection模型的拟合与改进

θ Projection模型将蠕变过程视为蠕变硬化和加速蠕变2个阶段，分别采用指数函数来描述，其表达式为

ε=θ1(1-e-θ2t)+θ3(eθ4t-1)

(7)

lgθi=ai+biσ+ciT+di(σ T)i=1,2,3,4

(8)

式中，ai、bi、ci、di为系数。

式(7)为蠕变曲线方程，即应变ε与时间t之间的关系。其中，θ1、θ2、θ3、θ4为参数，它们都可表示为温度T和应力σ的函数，如式(8)所示。若温度不变，式(8)仅为应力的函数，则最少只需测得2条不同应力下的蠕变曲线即可得到全部常数。

采用θ Projection模型拟合的马氏体钢母材100 MPa下的蠕变曲线和蠕变速率曲线如图6所示。

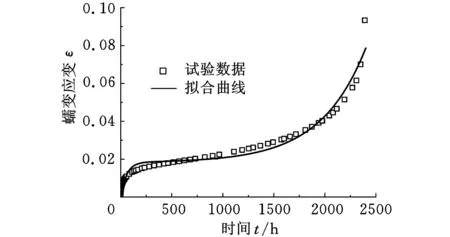
(a)蠕变曲线

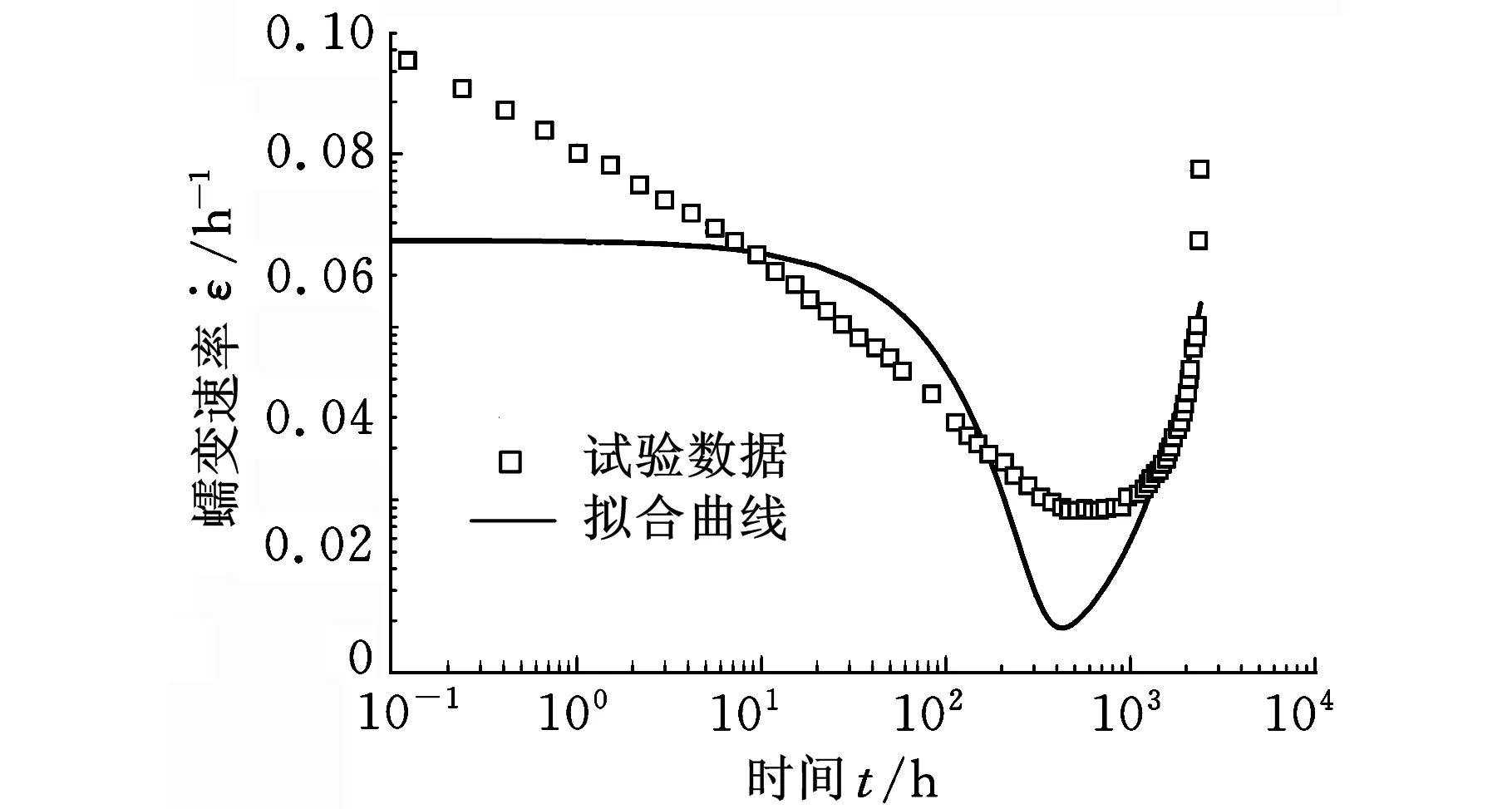
(b)蠕变速率曲线图6　θ Projection模型对马氏体钢蠕变数据的拟合结果

由图6可见θ Projection模型的拟合效果并不理想，主要原因是蠕变硬化阶段的蠕变速率与试验数据差别过大，而且最小蠕变速率也远低于实际值。由图6b可见，蠕变硬化阶段的蠕变速率在对数坐标下近似呈直线，应符合幂函数形式，因此蠕变曲线在硬化阶段也应符合幂函数形式。考虑到θ Projection模型对加速蠕变阶段的拟合度较好，因此保留θ Projection模型的加速蠕变项，而将硬化阶段改为幂函数形式。改进后的θ Projection模型表达式为

ε=θ1σθ2tθ3+θ4(eθ5t-1)

(9)

其中，θ1、θ2、θ3为材料常数，θ4、θ5为温度和应力的函数，表达式见式(8)。用改进后的θ Projection模型拟合马氏体钢母材在600 ℃、100 MPa下的蠕变曲线和蠕变速率曲线，并与改进前的拟合结果进行对比，如图7所示。

(a)蠕变曲线

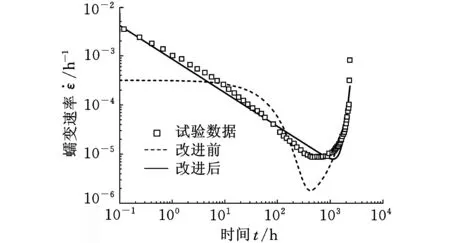
(b)蠕变速率曲线图7　改进前后的θ Projection模型对蠕变数据拟合结果对比

由图7可见，改进后的θ Projection模型在蠕变硬化阶段具有良好的拟合精度，而且最小蠕变速率与实际值很接近，蠕变加速阶段蠕变速率的陡升特性也与实际相符，只是加速阶段开始时间比试验结果略晚。

与K-R蠕变损伤模型相比，改进后的θ Projection蠕变模型不仅同样获得了良好的拟合度，而且保持了简洁的表达式形式，对有限元计算比较有利。但是K-R蠕变损伤模型可以预测构件发生蠕变损伤的部位和程度，仍具有一定优势。下面分别采用以上两种模型对焊接接头的蠕变行为进行模拟。

3　蠕变过程的有限元模拟

3.1材料弹性模量的确定

除上文中拟合得到的蠕变模型外，进行弹性范围内的蠕变模拟还需要知道材料的弹性模量和泊松比。泊松比通常取0.3，而弹性模量的测试存在困难。过渡层成分梯度很大，尺寸又很小，常规拉伸试验只能反映过渡层的平均弹性模量，而无法体现材料的不均匀性。因此，本文采用通过显微硬度换算弹性模量的方法。Bao等[12]研究了硬度测量过程中的外力做功、能量耗散与材料弹性恢复，提出了弹性模量与硬度之间的理论关系：

(10)

其中，H为硬度，F为常数，Rs为恢复阻力。对于Berkovich或Vickers压头，F取0.6647。Er为接触模量，其表达式为

(11)

其中，E、μ分别为被测材料的弹性模量和泊松比，Ei、μi分别为压头的弹性模量和泊松比。式(10)中的Rs反映的是材料在加载和卸载过程中的能量耗散，其表达式为

(12)

式中，pm为加载时的最大载荷；hs为压痕边缘线在载荷方向上的弹性恢复位移。

由于本文研究的焊接接头各部位均属于CrMoV系耐热钢，具有相似的弹塑性特征，可以假设其具有相同的恢复阻力。因此，根据式(10)，接触模量与硬度的平方根成正比。利用对整个接头的显微硬度测试结果，以及对均匀母材的弹性模量测试结果，可以换算出不同部位的接触模量，再通过式(11)推算出各部位的弹性模量，如图8所示。

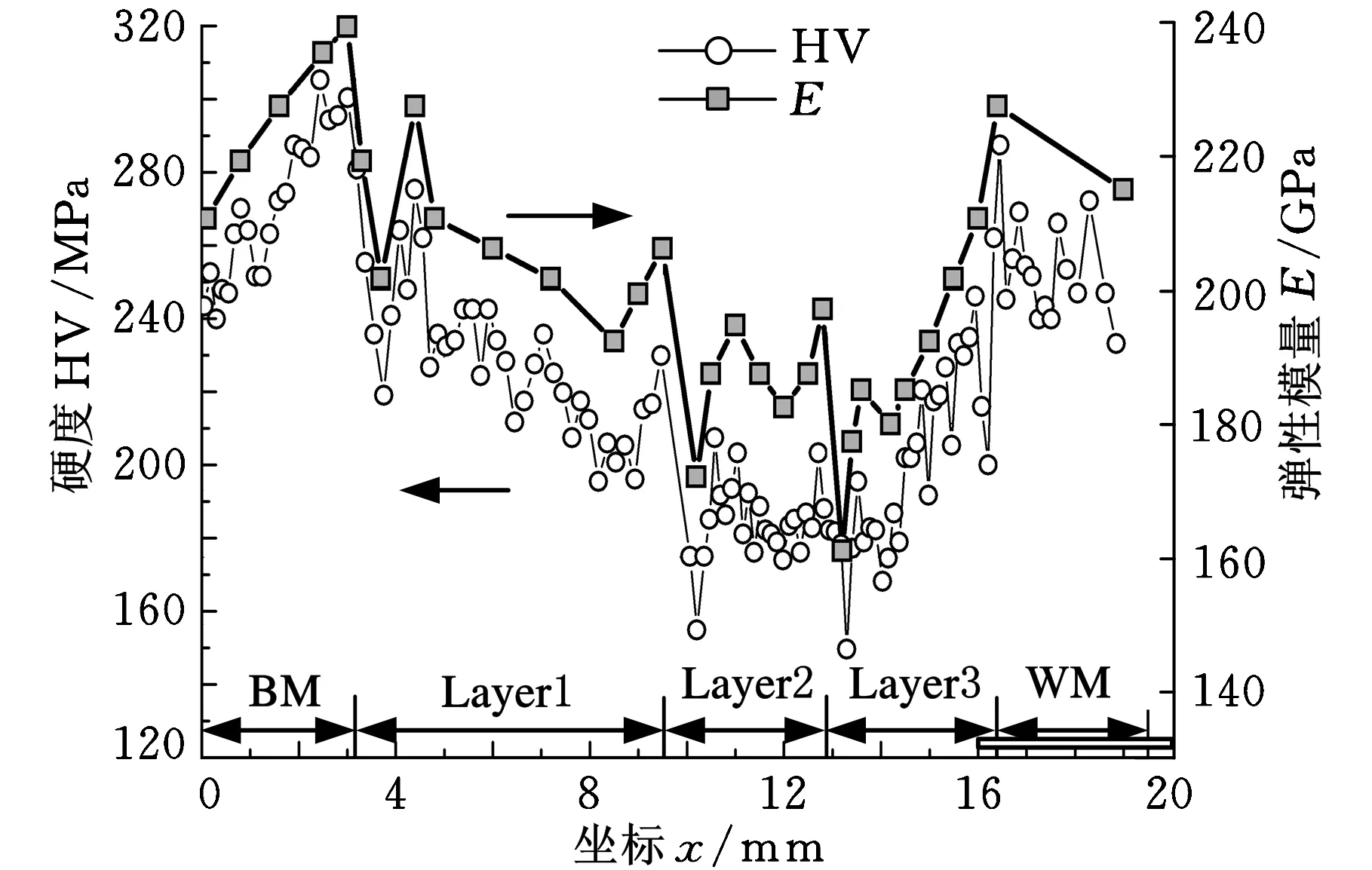
图8　接头硬度分布与弹性模量的计算

图8中包含马氏体钢母材、焊缝和3层过渡层的显微硬度测试数据。根据硬度的变化趋势，将接头离散成31层，每层根据其平均硬度换算弹性模量。这样可以完整地表现出各层过渡层熔合区的软化层、热影响区的淬硬区、正火区、回火软化区等区域的不均匀性。

3.2焊接接头的有限元建模

典型的焊接接头高温持久试样断口附近的解剖金相照片如图3所示。以图3中的过渡层结构为依据在ABAQUS软件中进行建模，采用平面应变模型，在一侧施加120 MPa拉伸载荷，如图9所示。

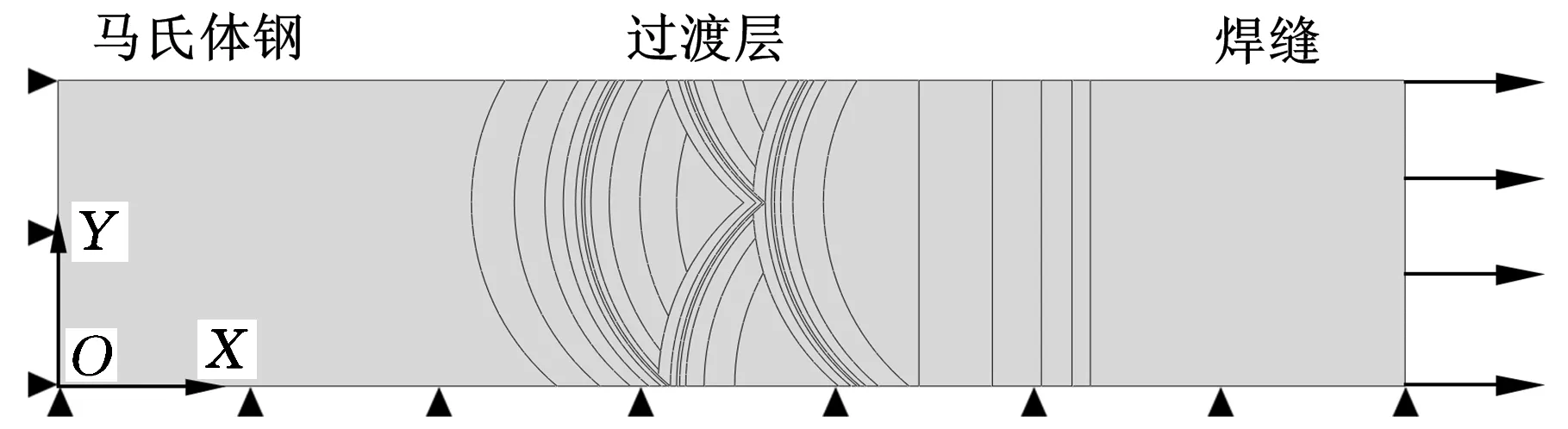
图9　焊接接头几何模型、载荷及边界条件

图9中包含马氏体钢母材、焊缝以及交错排列的3层过渡层。根据弹性模量的变化，在各层熔合区附近的软化层部位细分了多层结构，并减小网格尺寸，以更好地体现材料的非均匀性，如图10所示。

图10　焊接接头模型的网格划分

3.3焊接接头初始状态应力应变分布

在拉伸载荷作用下，焊接接头初始状态的应力应变分布如图11所示。

由图11可见，初始状态下硬度和弹性模量较低的过渡层区域整体应变较大，而且过渡层之间的熔合区软化层存在应变集中。另外，各层过渡层的淬硬区存在应力集中，特别是焊道交错排列形成的尖角处应力集中现象更加明显。

(a)Mises等效应力

(b)横向正应变图11　焊接接头初始状态应力应变分布

3.4两种蠕变模型的对比

经过1000 h蠕变后，两种蠕变模型的计算结果如图12所示。本文仅关注应变分布情况，因为蠕变失效往往是由应变决定的。

(a)蠕变损伤模型得到的横向正应变

(b)蠕变损伤模型的损伤变量

(c)改进型θ Projection模型得到的横向正应变图12　经1000 h蠕变后两种模型的计算结果(变形量放大15倍)

由图12可见，两种蠕变模型得到的应变分布类似，都是在较软的过渡层部分蠕变变形较大，并出现缩颈现象，但是θ Projection模型的变形程度更大。另外，过渡层熔合区软化层在初始状态下存在的应变集中现象，经过蠕变后得到缓解。这是因为蠕变应变逐渐增大，比初始状态的应变大2个数量级，因此软化层的应变集中现象被掩盖。

观察图3所示的实际断口，发现断裂发生在过渡层之间的熔合区，并在熔合区出现正在扩展的裂纹。由于有限元计算中没有引入裂纹的因素，只能反映出过渡层危险性较高。实际上在蠕变的开始阶段，应变集中的软化层可能出现微裂纹，成为过渡层中的薄弱环节。因此，两种模型对实际结构蠕变行为的预测都是合理的，但仍存在一定局限性。

以过渡层中最危险部位的应变为例，对比两种模型的差别，如图13所示。

图13　两种模型对过渡层中最危险部位应变的计算结果对比

由图13可见，改进型θ Projection模型的蠕变加速阶段出现时间较早，但蠕变率的增长比较平缓，而蠕变损伤模型的加速蠕变阶段出现较晚，但蠕变率突然快速增长。结合损伤变量的分析发现，采用蠕变损伤模型对加速蠕变开始时间的预测更为精确，而改进型θ Projection模型对应变的预测比较保守，安全性较高。

3.5材料非均匀性对蠕变行为的影响

非均匀结构的蠕变行为不同于均匀材料，这是因为结构各部分的蠕变特性不同，变形量存在差异，因此相互之间会产生拘束作用，出现复杂的多轴应力状态。为了研究材料非均匀性对结构蠕变行为的影响，将相同载荷下焊接接头中的焊缝内最危险部位的蠕变曲线与均匀焊缝材料的蠕变曲线进行对比，如图14所示。

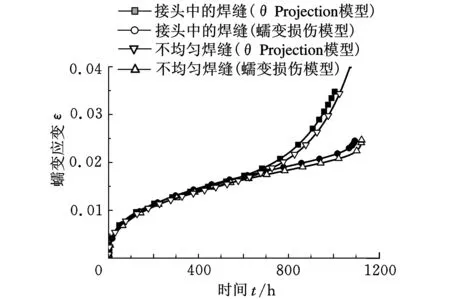
图14　接头中的焊缝与均匀焊缝材料蠕变曲线对比

由图14可见，两种模型的计算结果都显示，在焊接接头中的焊缝的蠕变量要大于均匀的焊缝材料的蠕变量。这说明材料的非均匀性会使结构整体的持久性能比其中最弱的单一材料更弱。

4　结论

(1)K-R蠕变损伤模型和改进型θ Projection模型对马氏体钢与珠光体钢异种接头中各部分材料的蠕变数据都能获得良好的拟合结果。

(2)在非均匀结构的蠕变模拟中，蠕变硬化阶段两种模型计算结果基本相同。改进型θ Projection模型更早进入加速蠕变阶段，但应变速率增长比较平缓；K-R蠕变损伤模型加速蠕变阶段开始较晚，但应变速率快速增长。K-R模型对加速蠕变阶段开始时间的预测比较精确，而改进型θ Projection模型安全性更高。

(3)两种模型的计算结果都表明，非均匀结构整体的持久性能要比其中最弱的单一材料更弱。因此，用各部分材料分别做蠕变试验来预测结构整体的蠕变特性是不可靠的，应采用蠕变试验与有限元计算相结合的方法进行寿命预测。

[1]马琰, 陈兰.异种金属焊接技术的应用实践[J].中国新技术新产品, 2011(19): 159.

Ma Yan, Chen Lan.Applications of Dissimilar Joint Welding Technologies[J].China New Technologies and Products, 2011(19): 159.

[2]Lundin C D.Dissimilar Metal Welds-transition Joints Literature Review[J].Welding Journal, 1982, 61(S2): 58-63.

[3]史春元, 范英, 陈字刚,等.模拟异种钢接头蠕变力学特性的数值分析[J].大连铁道学院学报,1994, 15(4): 84-88.

Shi Chunyuan, Fan Ying, Chen Zigang, et al. Numerical Analysis of Creep Mechanical Characteristics of Simulated Dissimilar Metal Welded Joints[J].Journal of Dalian Railway Institute, 1994, 15(4): 84-88.

[4]张建强, 郭嘉琳, 张国栋, 等.马氏体/珠光体异种耐热钢焊接接头蠕变失效数值模拟[J].焊接学报,2009,30(2):87-90.

Zhang Jianqiang, Guo Jialin, Zhang Guodong, et al. Numerical Simulation on Creep Failure of Dissimilar Welded Joint between Martensitic Heat-resistant Steel and Pearlitic Heat-resistant Steel[J].Transactions of the China Welding Institution, 2009, 30(2): 87-90.

[5]Kachanov L M.On Time to Rupture in Creep Condition (in Russian)[J].Izviiestia Akademii Nauk SSSR, Otdelenie Tekhnicheskikh Nauk, 1958,8(1):26-31.[6]Hayhurst D R. Creep Rupture under Multi-axial States of Stress[J].J. Mech. Phys. Solids, 1972, 20(6): 381-390.

[7]Johnson A E. Complex-stress Creep of Metals[J].Metallurg. Rev., 1960, 5(20): 447-506.

[8]刘学, 段向兵, 闫平, 等. P91钢高温蠕变的数值研究[J]. 电力建设, 2009, 30(5): 52-55.

Liu Xue, Duan Xiangbing, Yan Pin,et al.Numerical Study of P91 Steel High Temperature Creep[J].Electric Power Construction, 2009, 30(5): 52-55.

[9]张俊善.材料的高温变形与断裂[M].北京: 科学出版社, 2007.

[10]张建强, 张国栋, 姚兵印, 等.T91/HR3C异种耐热钢焊接接头蠕变失效有限元模拟[J].焊接学报, 2013, 34(7): 68-72.

Zhang Jianqiang, Zhang Guodong, Yao Bingyin, et al. Numerical Simulation on Creep Failure of T91/HR3C Heat-resistant Steels Welded Joint[J].Transactions of the China Welding Institution, 2013, 34(7): 68-72.

[11]Sunil-Goyal, Laha K, ChandravathiK S, et al.Prediction of Type IV Cracking Behaviour of 2.25Cr-1Mo Steel Weld Joint Based on Finite Element Analysis[J].Transaction of the Indian Institute of Metals, 2010, 63(2/3): 461-466.

[12]Bao Y W, Wang W, Zhou Y C.Investigation of the Relationship between Elastic Modulus and Hardness Based on Depth-sensing Indentation Measurements[J].Acta Materialia, 2004, 52(18): 5397-5404.

(编辑陈勇)

Finite Element Analysis of Creep Behavior of Dissimilar Steel Welded Joint

Zhang BoqiCai ZhipengLi KejianLi YifeiPan Jiluan

Tsinghua University,Beijing,100084

Dissimilar welded joints are often used in large components working under high temperature. The creep rupture property of dissimilar welded joint is of great significance for the safety of the structure. Conventional creep test and creep rupture test are only applicable to homogeneous materials, but not to inhomogeneous materials. In order to solve this problem, a finite element model was built according to a dissimilar welded joint used in a real component which made up of martensitic steel and pearlitic steel.By using K-R creep damage model and advanced θ Projection model respectively, it is found that the creep rupture property of inhomogeneous dissimilar joint is different from that of homogeneous base metal, weld metal and transition layer. The creep rate of transition layer in dissimilar joint is higher than the same homogeneous material, which means the heterogeneity of structure leads to additional creep damage. The conclusion can be made that it is unreliable to predict the creep life of a dissimilar steel structure only according to creep rupture tests on different parts for homogenous materials,the finite elements analysis based on creep rupture test is also necessary.

dissimilar steel welding; heterogeneous material; creep simulation; finite element analysis

2014-01-22

TG407DOI：10.3969/j.issn.1004-132X.2015.02.025

张伯奇，男，1986年生。清华大学机械工程学院博士研究生。主要研究方向为焊接冶金等。发表论文6篇，获国家专利2项。蔡志鹏，男，1974年生。清华大学机械工程学院副研究员。李克俭，男，1989年生。清华大学机械工程学院博士研究生。李轶非，男，1989年生。清华大学机械工程学院博士研究生。潘际銮，男，1927年生。中国科学院院士，清华大学机械工程学院教授、博士研究生导师。