基于颤振试验数据分析的矩阵束方法性能研究

谭　博　郑　华

西北工业大学,西安,710072

基于颤振试验数据分析的矩阵束方法性能研究

谭博郑华

西北工业大学,西安,710072

为将矩阵束引入颤振试验数据处理的工程应用领域,基于随机信号仿真,采用蒙特卡罗方法分析了该方法的数值性能,研究了样本长度、信噪比及计算参数对计算性能的影响,并在飞机机翼气弹模型的风洞颤振试验中进行了验证。与传统频域方法的比较分析表明,矩阵束方法性能良好,是一种可靠的模态参数估计方法。

矩阵束;蒙特卡罗方法;模态参数识别;颤振试验数据分析

0　引言

飞机结构颤振是飞机研制过程中必须进行的实验科目,具有风险高、周期长等特点，且其观测信号具有有效样本短、信噪比小、结构模态密集等特征，从而使得如何从实际观测数据中提取结构模态参数成为该行业十分关注的问题。

矩阵束方法作为一种模态参数估计方法,在许多领域有了广泛应用。但是，在引入飞机结构颤振试验时,该方法的参数估计质量经常会受到样本长度、信噪比等的影响。为此，本文基于随机信号仿真,应用蒙特卡罗方法对其相关的数值性能进行了分析研究。

1　矩阵束方法简介

假设观测到的系统响应信号可表示为M个模态的指数函数的线性组合：

(1)

其中,x(t)、n(t)、y(t)分别为系统响应、系统噪声和含噪声的实测信号,0≤t≤T;T为最大观测时间。对第i个模态,算子si=-αi+jωi可用于表示模态的频率和阻尼比系数,其中ωi为角频率,αi为阻尼比系数。

式(1)的离散时间形式为

(2)

k=0,1,2,…,N

其中,zi为系统响应的极点,zi=exp(siTs);Ts为采样周期;N为最大采样点数。

由采集序列y(t)可以构造如下的Hankel矩阵：

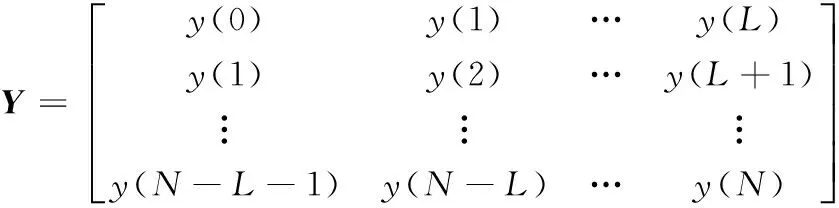
(3)

式中,L为矩阵束参数,通常取值位于N/4～N/3之间。

对矩阵Y进行奇异值分解,得到

Y=UDVT

(4)

式中,U为N-L阶正交矩阵;V为L+1阶正交矩阵;D为半正定的(N-L)×(L+1)阶对角阵，其主对角线上的元素为奇异值(由大至小排列)。

在已知模态个数M的情况下,由D的前M个较大的非零奇异值形成新的矩阵：

(5)

Δ=diag(δ1,δ2,…,δM)

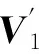
(6)

(7)

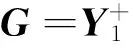
(8)

2　数值性能研究

2.1采样点数影响

处理试验数据时,依据不同的试验环境、结果精度、速度要求以及测试设备条件等设置不同的采样长度后，方能进行模态参数估计,而采样长度往往会影响最终数据处理结果。因此本文首先通过仿真数据来研究样本长度对矩阵束方法数值性能的影响。设置一个单模态自由度系统,其阻尼比系数为0.03,振动频率为11 Hz,激励信号为随机白噪声，响应信号的采样率为128,仿真信号的采样长度从1 s逐秒增加至60 s，针对每一个采样长度进行3000次运算，将计算所得模态的频率和阻尼比进行统计，分别将其高斯分布中值作为最终结果,如图1、图2所示。图1与图2中，横轴表示采样点数，范围为128～7500,对应的采样时间为1～60 s。

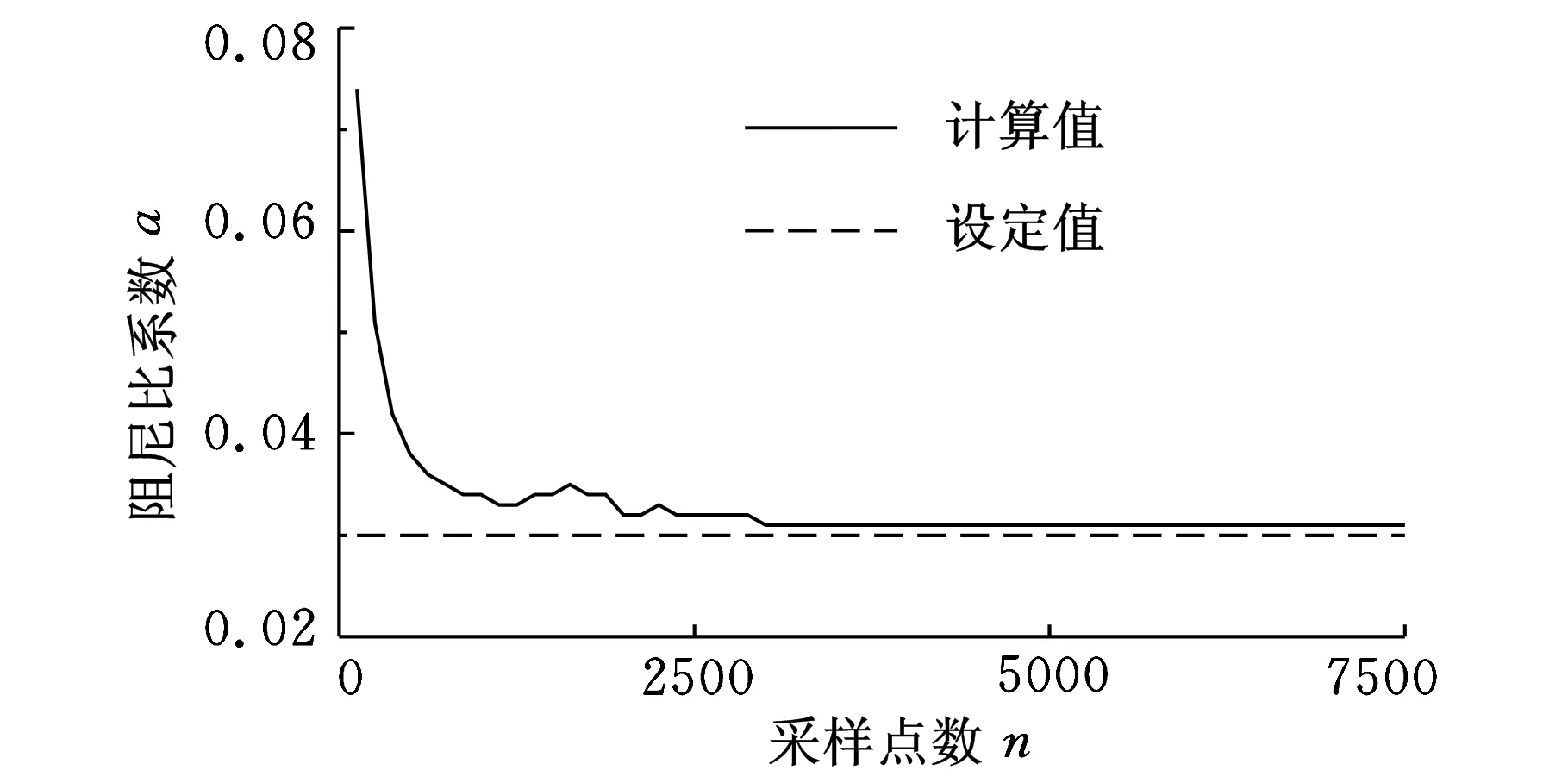
图1　计算阻尼比系数随采样点数变化曲线

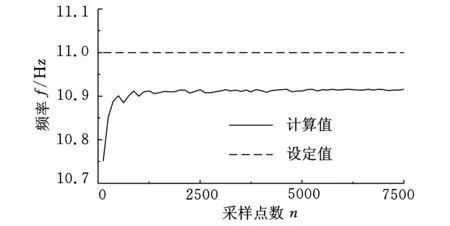
图2　计算频率随采样点数变化曲线

从图1、图2可以明显看出,样本点过少会极大地影响矩阵束方法计算结果的精度,导致最终计算结果与设定真值相差过大。增加采样长度可提高计算结果的精度，使其接近真实值。当采样点数达到一定数量之后,单纯地增加采样点不能明显改善矩阵束方法的数值性能,反而会延长计算时间，导致系统的运行时间间隔增加，影响方法的计算效率。由于在飞机结构颤振试验中常有实时分析的要求，因此，采样点数的设置应在计算效率和结果精度之间做出平衡。

2.2信噪比对数值性能的影响

试验采集得到的信号总会受到噪声的影响。因此模态参数估计方法的抗噪性能也是选择方法时需考量的重点之一。

蒙特卡罗方法是一种通过对大量彼此独立的试验结果进行统计，得出统计对象数学特征的方法。由于实际中的试验周期较长,无法进行大量的重复试验，因此在本节中，将通过仿真信号对矩阵束方法在噪声环境下的性能进行研究。设置一个双模态自由度系统,模态参数分别设置为:f1=11 Hz,f2=13 Hz,d1=0.05,d2=0.04,f与d分别表示模态参数中的频率与阻尼,下标1、2表示模态1和模态2。将响应信号的信噪比依次置为无噪声(信噪比无穷大)、20 dB、10 dB、6 dB、3 dB和0,使用矩阵束方法对加噪后的信号进行模态参数估计运算,对所得结果进行统计,表1所示为3000次计算的统计结果。可以看出，矩阵束方法估计的模态参数中,频率受噪声影响较小,随着信噪比的下降没有发生明显变化，而估计所得阻尼随着信噪比的下降有较大变化。

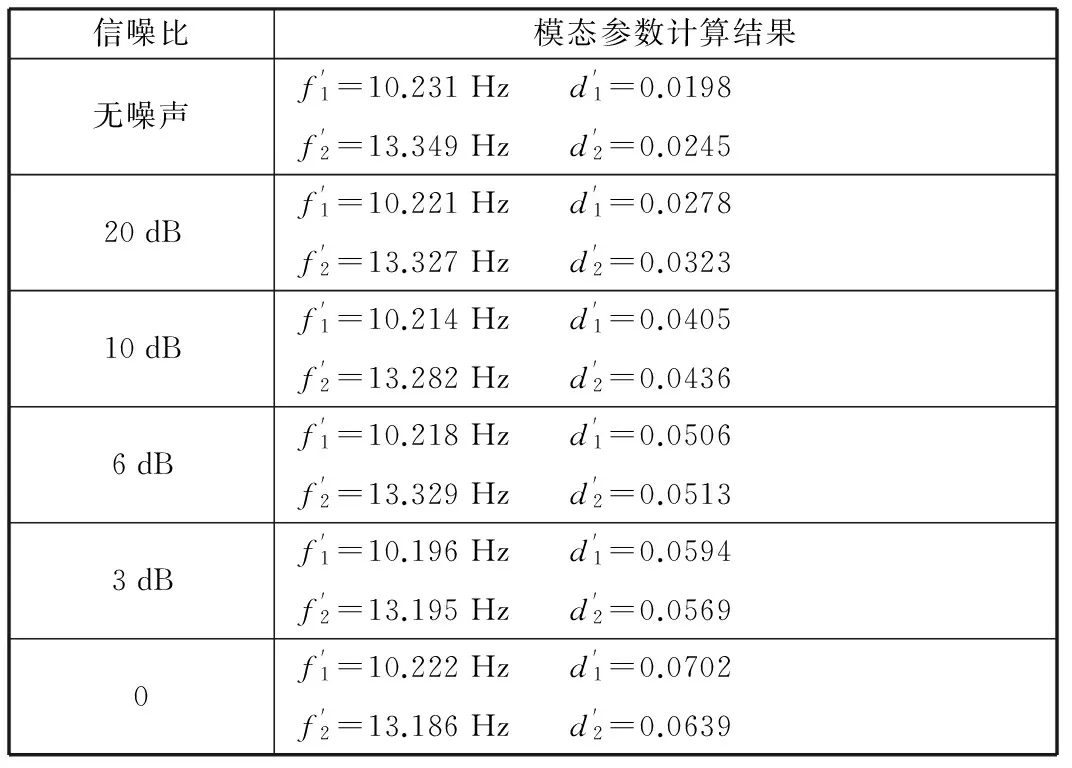
表1　不同信噪比下矩阵束方法的计算结果

2.3设置参数对数值性能的影响

从仿真实验结果可以看出,在仅改变信噪比的情况下，矩阵束方法所得的阻尼估计结果会产生较大的波动。为削弱噪声对矩阵束方法阻尼估计结果的影响，增强矩阵束方法的抗噪性能，可以适当调整方法的设置参数，即模态个数M。

模态个数M对应于运算时设置的极点个数。增加设置的模态个数M,会导致最终计算结果中出现实际系统中不存在的虚假模态，但可有效地削弱噪声对真实模态的计算结果的影响。

下面以1个三模态自由度且有密集模态的系统为例，说明改变参数对矩阵束方法的数值性能的影响。系统的3个模态的参数设置分别为:f1=11 Hz,f2=12 Hz,f3=17 Hz,d1=0.05,d2=0.04,d3=0.01,其中,11 Hz、12 Hz的模态为系统的密集模态频率。为系统的响应信号添加信噪比为6 dB的噪声后得到采集信号。

(a)M=3

(b)M=5

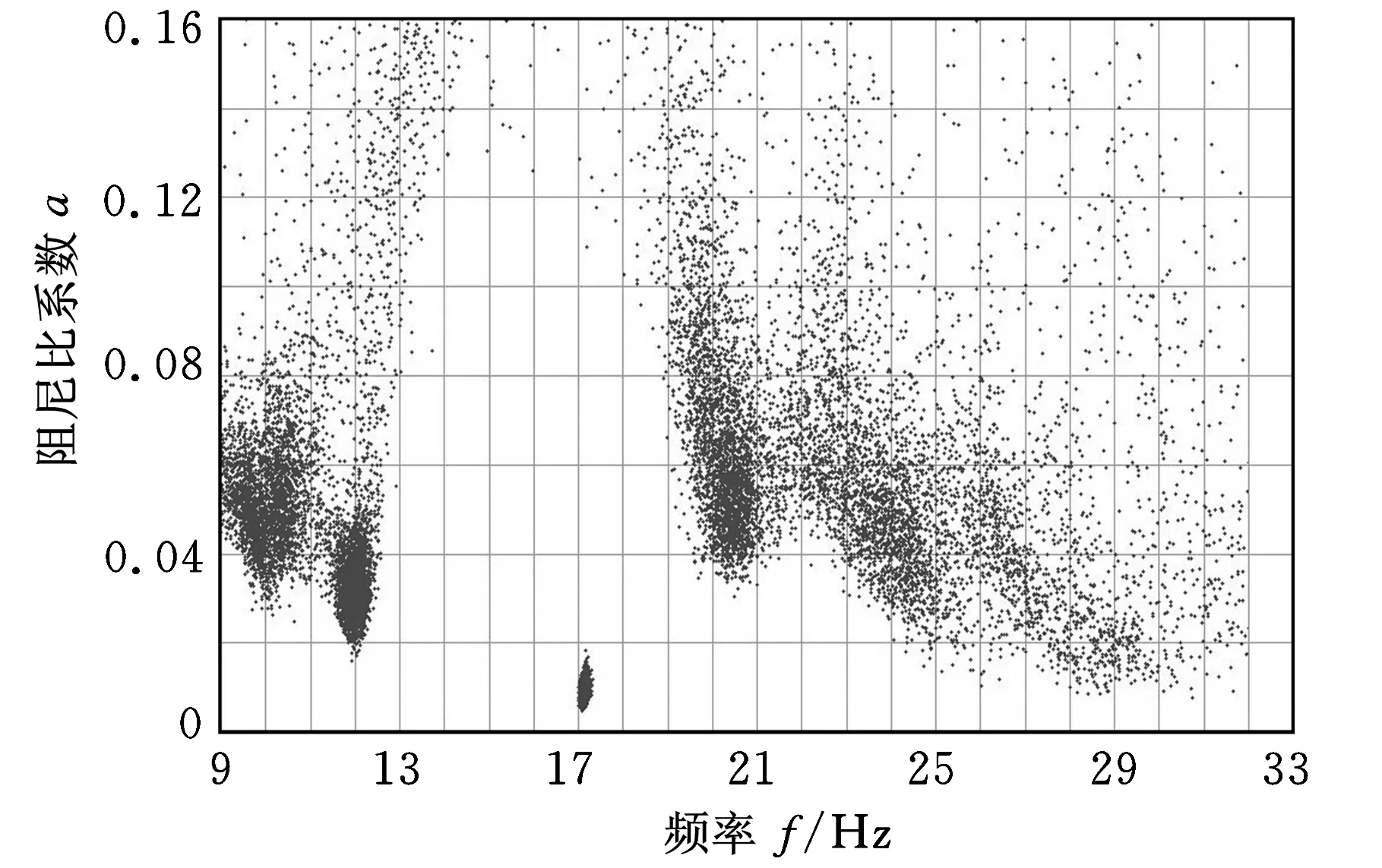
(c)M=6图3　矩阵束方法估计结果分布

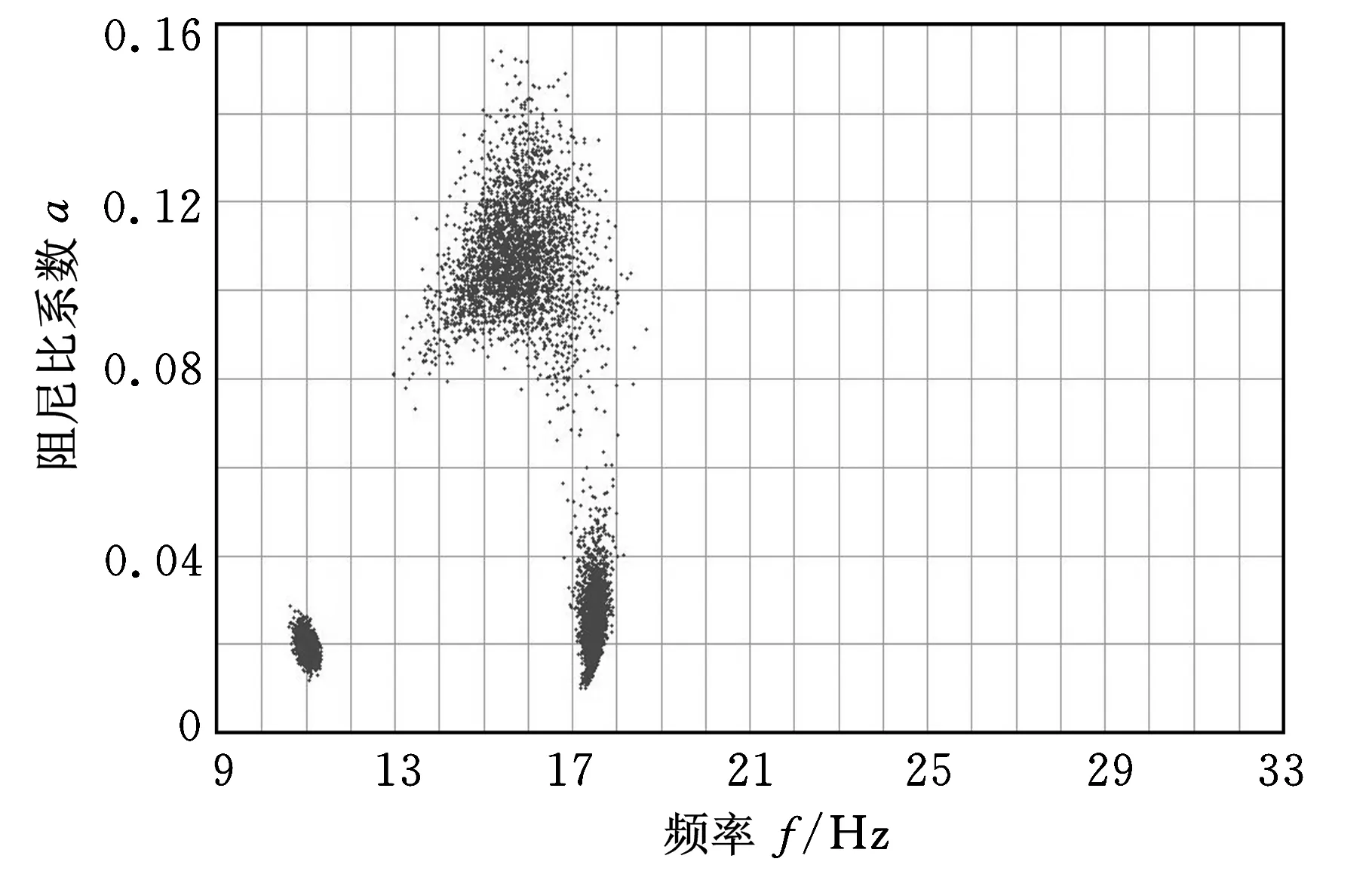
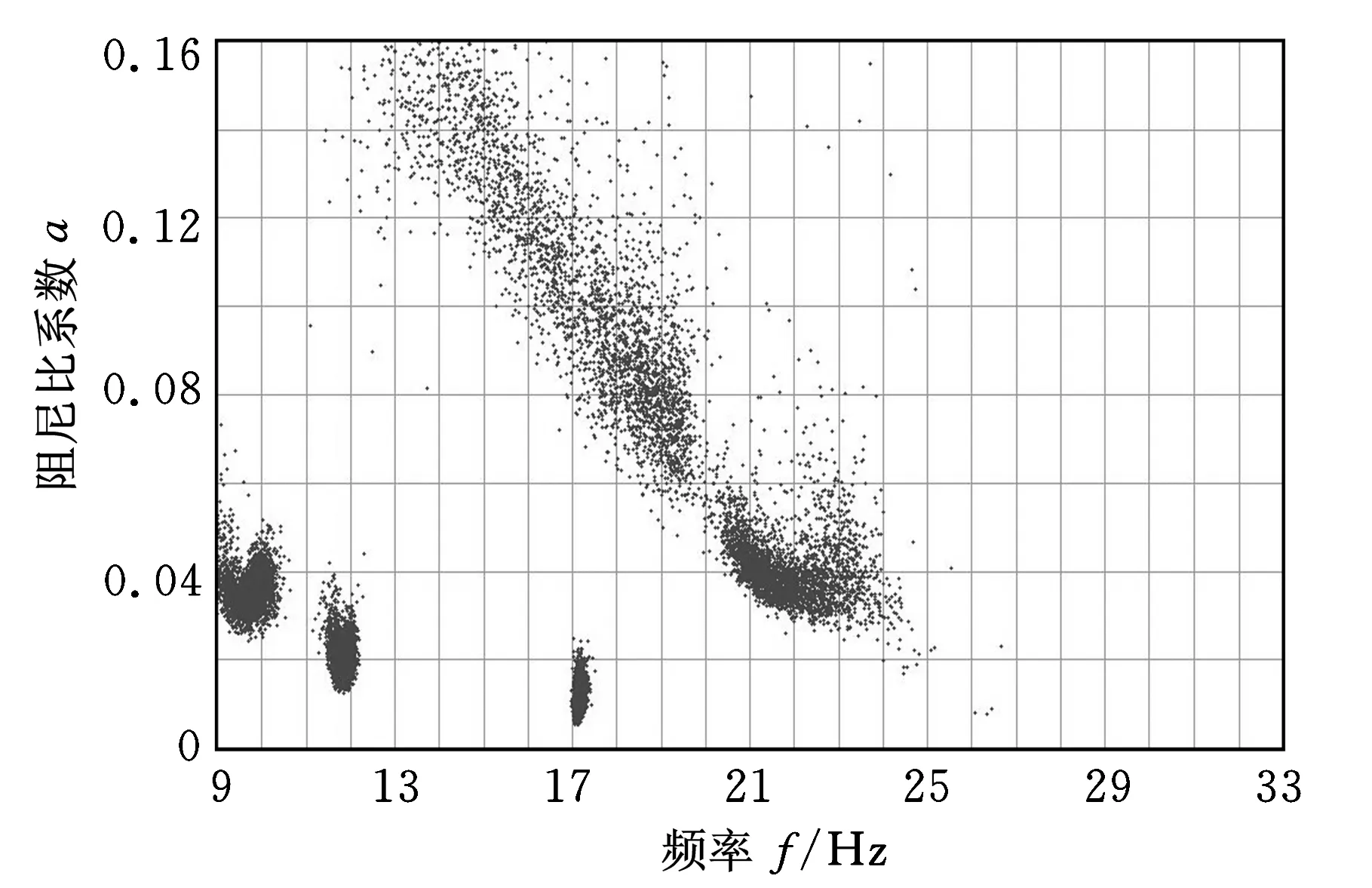
图3所示为统计得到的计算结果分布情况,图中，横轴表示计算所得模态参数的频率,范围为9～33 Hz,纵轴为阻尼比系数，范围为0～0.16。图3中的每个点代表通过矩阵束计算得到的一个模态。

图3a所示为M=3的结果分布情况,可以看出,由于受到噪声的干扰，系统的2个密集模态较难分辨,但是可以清晰地分辨出设计系统位于17 Hz的模态。图3b所示为M=5的计算结果分布,可以看到当设置模态个数增加到5后,矩阵束方法对系统的2个密集模态有了较好的分辨能力,同时17 Hz的模态仍然被可以清晰地进行辨识,图中右上方分布的计算结果点即为矩阵束方法计算结果中的虚假模态。将图3a、图3b进行比较后不难发现，图3b所示的计算结果相较图3a的结果更加接近设定系统的真实值，其分布也更加集中，这表明，增加模态个数不仅可以减小计算结果的误差，而且可以减小结果的统计方差。在结构颤振试验中，采集信号往往长度有限，处理数据时难以采用多次计算后进行统计的方式来减小误差，在这样的背景下，减小计算结果的统计方差可以增加结果的置信度。

图3c所示为将模态个数再次增加后的计算结果分布。由图3b、图3c的比较可以看出，此时设置的模态个数为实际模态个数的2倍,尽管系统的2个密集模态仍可较为清晰地分辨出来，但是其结果分布明显比图3b所示结果更分散。这表示矩阵束方法的计算结果会在一个较大的范围内波动，降低了计算结果的置信度，不利于确定系统的模态参数。因此若模态个数设置过大，反而会降低矩阵束方法的结果的估计精度，而且增加模态参数的个数会延长系统的运算间隔，降低计算效率，导致系统成本的增加，因此应避免设置模态数过大。

3　在颤振试验数据分析中的应用

本文使用的试验数据由某型飞机模型风洞试验数据得来。经零均值化处理后，选取颤振发生前的5个速度对应的5段数据作为计算依据,分别应用矩阵束法与半功率带宽法对数据进行分析，给出拟合曲线以及预测结果。本次使用的试验数据中，将颤振发生时的风速设置为1，其余各速度依此进行归一化处理。颤振发生时刻采集信号的时域波形及频谱如图4所示。

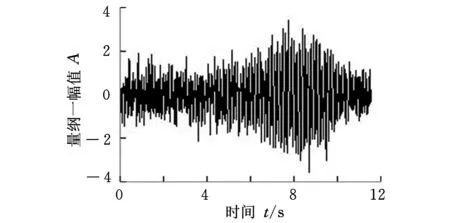
(a)时域波形

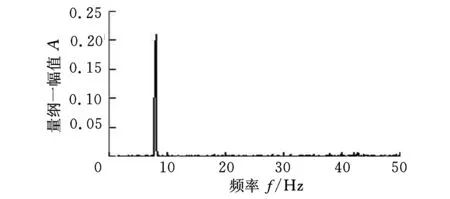
(b)频谱图图4　颤振发生时的采集信号

由图4可以看到,颤振发生时信号能量集中于8 Hz附近。依次使用矩阵束法和半功率带宽法对颤振临界点前的五段数据进行模态分析计算,对结果进行拟合后得到的曲线如图5所示。

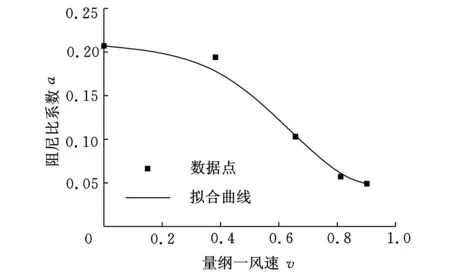
(a)矩阵束方法

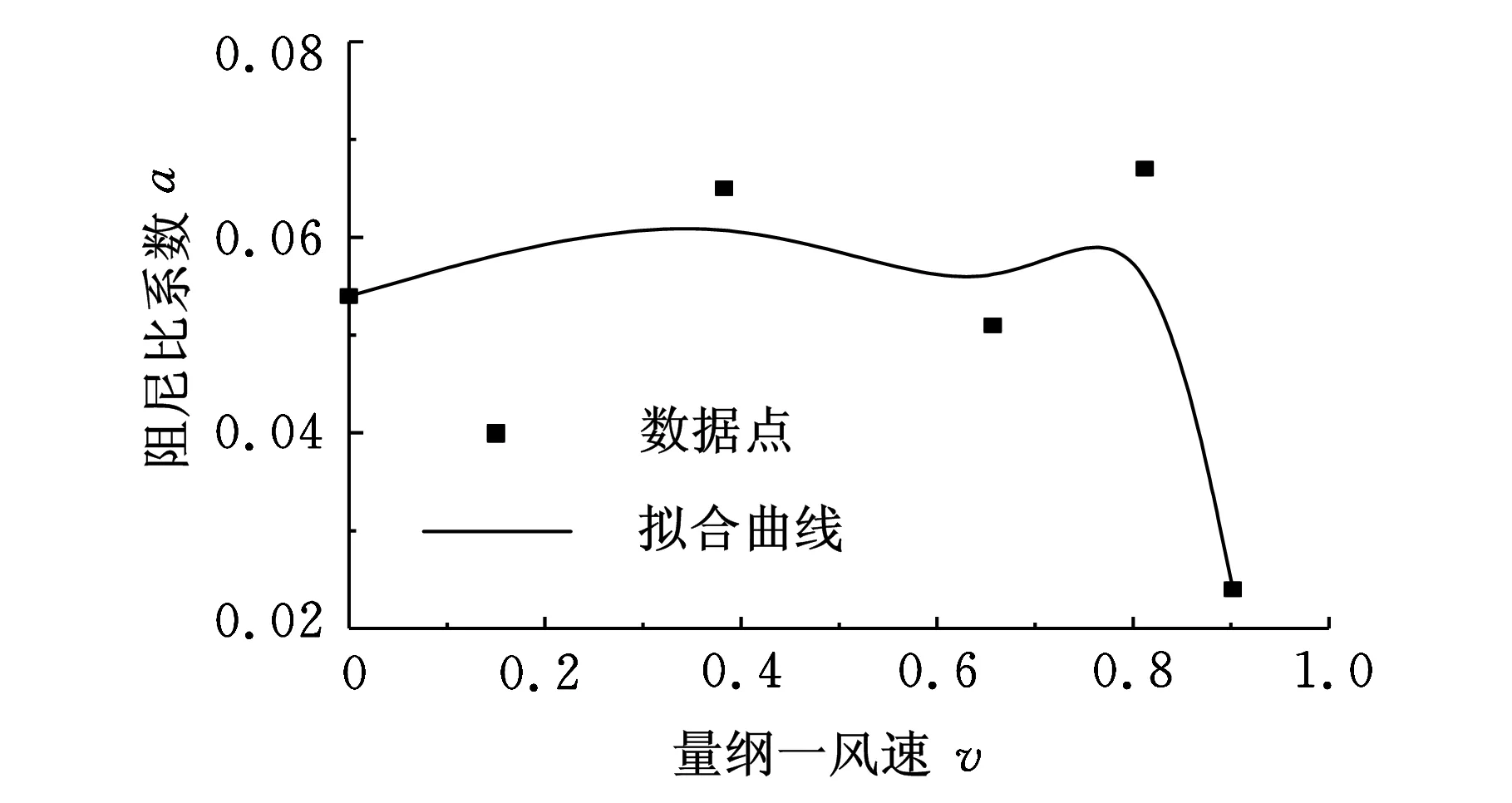
(b)半功率带宽法图5　两种计算方法的拟合结果

对比图5a、图5b可以看出，合理选择算法参数后，矩阵束方法计算得到的阻尼结果趋势较明显，其最终估计的颤振速度为0.993，与真实值相差较小；半功率带宽法的计算结果波动较大，拟合曲线不平滑，其最后估计的颤振速度为1.103，与真实值相差较大。产生这一结果的主要原因是，对于密集模态而言，半功率带宽法受到自身算法的数学特性的限制，难以对模态之间的边界进行清晰的区分,因此其对密集模态的分辨效果不如矩阵束法好，计算阻尼和真实值偏差较大。结构颤振试验中，密集模态的分辨问题是一个经常面对的问题,这也是半功率带宽法在飞机结构颤振试验中表现不佳，需要引入矩阵束法的原因之一。

4　结语

在保证系统运算效率的前提下，增加采样点数可以提高矩阵束方法的计算精度；矩阵束方法用于模态参数估计时，其得到的频率估计结果受到噪声影响较小，且相对于阻尼比系数估计结果更加稳定；在检测信号含有噪声的情况下，可以适当增大模态个数，用虚假模态来削弱噪声的影响，以有效改善最终结果。

颤振试验数据的处理结果表明，在模态阻尼比估计中，矩阵束法计算结果比较理想，其拟合曲线较为平滑，而且与传统的半功率带宽法相比，其估计结果具有更高的数值精度。

[1]Hua Yingbo,Sarkar Tapan K.Matrix Pencil Method for Estimation Parameters of Exponentially Damped/undamped Sinusoids in Noise[J].IEEE Transactions on Acoustics Speech and Signal Processing,1990,38(5):814-824.

[2]Thomas A J,Chard J,John E,et al.Defining a Bearing Replacement Strategy Using Monte Carlo Methods[J].International Journal of Quality & Reliability Management,2011,28(2):155-167.

[3]Potts D,Tasche M.Parameter Estimation for Nonincreasing Exponential Sums by Prony-like Methods[C]//17th Conference of the International Linear Algebra Society.Braunschweig,Germany,2013:1024-1039.

[4]朱瑞可,李兴源,王渝红,等.基于矩阵束算法的谐波和间谐波参数估计[J].计算机仿真,2012,40(3):388-391.

Zhu Ruike,Li Xingyuan,Wang Yuhong,et al.Parameter Identification of Harmonics and Interharmonics Based on Matrix Pencil Algorithm[J].East China Electric Power,2012,40(3):388-391.

[5]张敏，黄俐，李文雄，等.大型结构模态参数识别研究[J]，建筑科学与工程学报，2013，30(2)：49-54，75.

Zhang Min，Huang Li，Li Wenxiong，et al. Research on Modal Parameter Identification on Large-scale Structure[J]. Journal of Architecture and Civil Engineering，2013，30(2)：49-54，75.

[6]徐利,邹传云，陈民，等. 基于矩阵束算法的极点提取分析[J]. 通信技术，2012，45(6)：58-60.

Xu Li,Zou Chuanyun,Chen Min,et al.Analysis on Pole Extraction Based on Matrix Pencil Algorithm [J].Communications Technology，2012，45(6)：58-60.

[7]贾天娇，岳林. 一种模态弱响应且模态秘籍的参数识别方法[J]. 中国机械工程，2012，23(11)：1313-1317.

Jia Tianjiao，Yue Lin. A Parameter Identification Method for Weak Modal Response with Close Modes[J]. China Mechanical Engineering，2012，23(11)：1313-1317.

[8]杨明华,奇异矩阵束的标准形与广义逆[D]. 哈尔滨：哈尔滨工业大学,2013.

[9]郑敏,申凡,史东锋,等.单独利用响应数据进行模态分析[J]. 中国机械工程,2006,17(4):405-409.

Zheng Min,Shen Fan,Shi Dongfeng,et al.Modal Analysis from Response-only[J].China Mechanical Engineering,2006,17(4)：405-409.

[10]黄应来,董大伟,闫兵.密集模态分离及其参数识别方法研究[J].机械强度,2009,31(1):8-13.

Huang Yinglai,Dong Dawei,Yan Bing.Study on Closely Spaced Modes Decomposition and Modal Parameter Identification[J].Journal of Mechanical Strength,2009,31(1):8-13.

(编辑张洋)

Research on Numerical Performance of Matrix Pencil Based on Flutter Test Analysis

Tan BoZheng Hua

Northwestern Polytechnical University,Xi’an,710072

In order to apply MP algorithm into flutter test data processing,the characteristics were studied through Monte Carlo method,the effects of signal length,signal-noise ratio and parameters were mainly concerned.Then MP algorithm was tested with real collected data from physical experiments.The results show that MP is a valuable method to identify modal parameters for flutter test analyzses compared with traditional ways of data processing.

matrix pencil(MP);Monte Carlo method;modal parameter identification;flutter test

2013-10-10

国家自然科学基金资助项目(11302175)

TP391.9DOI：10.3969/j.issn.1004-132X.2015.02.019

谭博,男,1987年生。西北工业大学动力与能源学院博士研究生。主要研究方向为人机环境与工程。发表论文7篇。郑华,男,1983年生。西北工业大学动力与能源学院博士后研究人员。