基于改进蚁群算法的带时间窗废品收集车辆路径问题
刘 琼 刘秀城 张超勇 饶运清
华中科技大学数字制造装备与技术国家重点实验室,武汉,430074
基于改进蚁群算法的带时间窗废品收集车辆路径问题
刘琼刘秀城张超勇饶运清
华中科技大学数字制造装备与技术国家重点实验室,武汉,430074
建立了以最小化燃油消耗为优化目标的带时间窗、司机休息时间以及多个中转处理中心的废品收集车辆路径问题模型。提出了一种改进最大最小蚁群算法,针对时间窗特点,设计了两类满足时间窗约束的动态候选列表以提高算法的搜索效率。在最大最小蚁群算法的概率状态转移规则中引入了带距离限制的最近邻域搜索。10个基准实例中的9个实例比当前文献的最优解更好,从而验证了该模型和算法的可行性和有效性。
大规模带时间窗车辆;路径问题;蚁群算法;燃油消耗
0 引言
有效的废品收集和处理对保护环境和节约资源有重要的意义。过去针对废品收集车辆路径问题,通常都是通过使废品收集车辆运输时间或运输距离最短,来达到降低总费用的目的,如Sahoo等[1]建立的带有时间窗、司机午餐休息时间以及多个中转废品处理中心的最小化车辆运输时间的废品收集车辆路径问题模型和Angelelli等[2]提出的车辆容量不同、多个废品处理中心的最小化车辆运输距离的多周期废品收集车辆路径问题模型。由于车辆运输所产生的运输费用直接取决于车辆燃油消耗,而影响车辆燃油消耗费用的因素除车辆运输距离外,还涉及车辆载重、车速、道路倾斜度和轮胎状况等因素[3]。因此,目前车辆路径优化问题中普遍考虑的车辆运输距离或运输时间往往不能准确反映车辆的实际运输费用,还必须考虑对燃油消耗具有较大影响的因素如车辆载重、车速等。目前,在车辆路径问题中已开始研究油耗问题,如Xiao等[4]在容量受限的车辆路径问题(capacitated vehicle routing problem,CVRP)中,分别以最小化油耗和最小化距离为优化目标对27个CVRP基准实例进行测试,结果表明:考虑车辆载重和距离的最小化燃油消耗的车辆路径问题与单纯以最小化车辆运输距离为优化目标的模型平均能降低5%的燃油消耗。但是,与一般的车辆路径问题不同的是,废品收集车辆路径问题中存在车辆达到满载时需要选取合适的废品处理中心进行废品清空等极大影响车辆载重及燃油消耗的问题。目前,在废品收集车辆点路径问题中考虑燃油消耗的研究还不多。Tavares等[5]在废品收集车辆路径问题中考虑道路倾斜度和车辆载重对燃油消耗的影响,以最小化燃油消耗为目标进行优化,与单纯以最小化车辆运输距离为优化目标的结果相比,减少了52%的燃油消耗,但该研究没有考虑车辆载重和燃油消耗之间的具体函数关系。Zsigraiova等[6]以车辆载重为变量,对废品收集车辆路径进行了灵敏性分析,分析结果表明,车辆载重的确对废品收集车辆路径问题中的燃油消耗有较大影响,但没有进行具体的路径优化。
废品收集车辆路径问题往往是包含大规模数据的NP难问题[1]。传统的精确算法无法在短时间内获得模型的满意解,因此较多地使用元启发式方法进行求解,如禁忌搜索、遗传算法和蚁群算法等。其中,蚁群算法是成功用于求解TSP(travelling salesman problem)的构造元启发式方法,但随着数据规模的增大,算法性能会急剧劣化。为了改善蚁群算法性能,Stützle等[7]提出了最大最小蚁群算法,该算法在求解较大数据规模的TSP等组合优化问题方面具有良好的性能而得到广泛研究。
为了准确分析车辆载重和车辆运输距离对废品收集车辆路径问题中燃油消耗的影响,本文在考虑车辆载重和车辆运输距离对燃油消耗影响的情况下,建立了带有时间窗、司机午餐休息时间以及多个中转废品处理中心的最小化燃油消耗的废品收集车辆路径问题模型。为了进一步提高最大最小蚁群算法求解大规模数据的废品收集车辆路径问题的效果,本文提出一种嵌入带距离限制的最近邻域搜索的最大最小蚁群算法,并采用两两交换局部搜索进行进一步优化。对基准实例的测试验证了所提出算法的有效性。
1 数学模型
1.1模型描述
带时间窗、司机午餐休息时间及多个中转废品处理中心的最小化燃油消耗的废品收集车辆路径问题模型可以用一张平面图G=(V,A,T)表示。其中,平面中的点集V={0,1,2,…,N+M+1},T表示V中每个点的时间窗约束,A为任意两端点之间线段的集合,0表示停车场P,N个顾客的集合S={1,2,…,N},M个废品处理中心的集合F={N+1,N+2,…,N+M},假设司机午餐休息时间为模型中的一个虚拟点,用LB={N+M+1}表示。模型参数见表1。图1是该模型的废品收集车辆运输路径示意图。
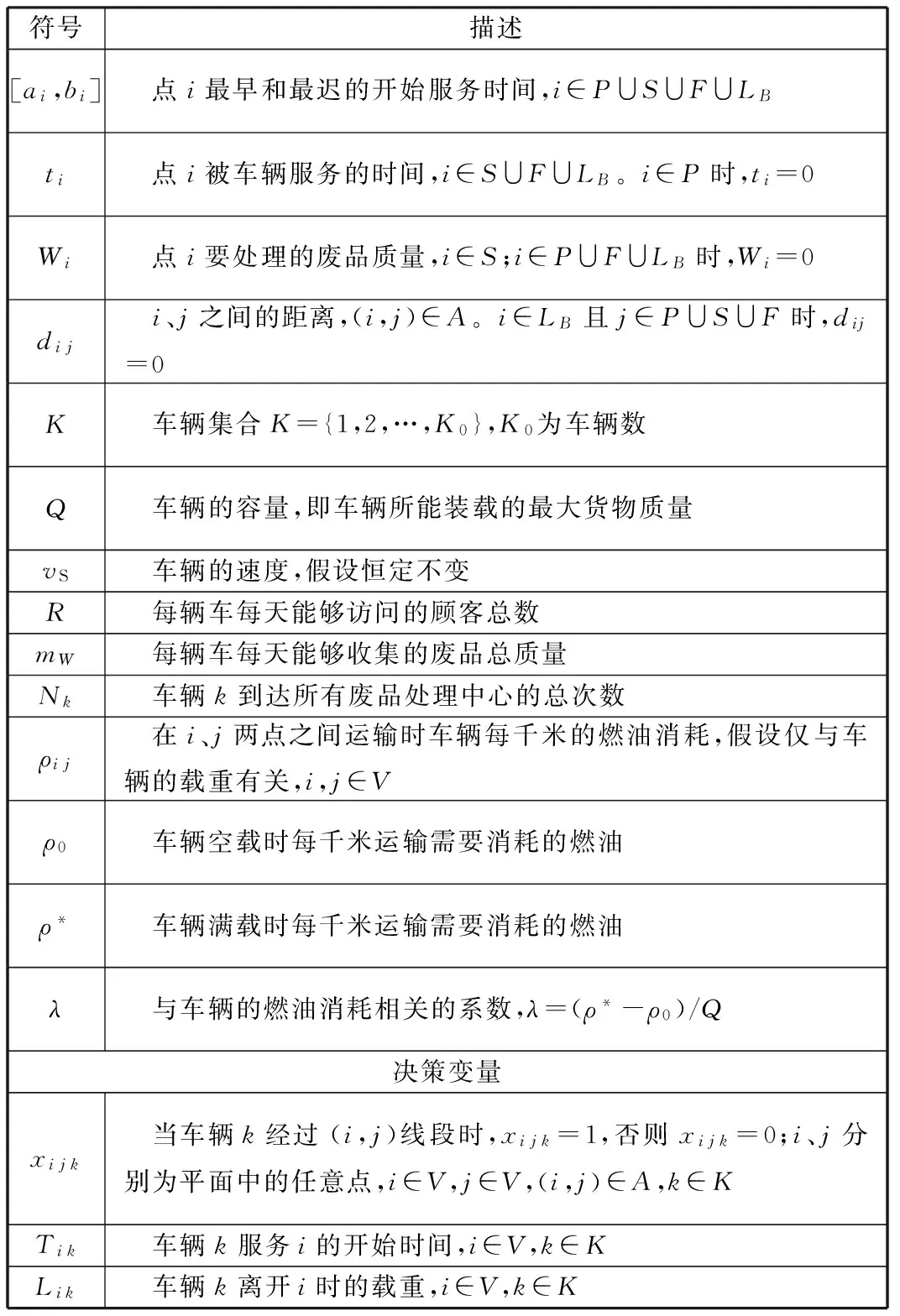
表1 模型参数
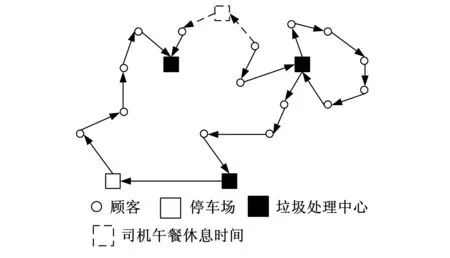
图1 废品收集车辆运输路径示意图
该模型的约束主要包括停车场、顾客和废品处理中心的时间窗约束,司机的午餐休息时间约束以及车辆和运输路径的容量约束等。具体如下:
(1)时间窗约束[ai,bi]指最早和最迟允许的开始服务时间。每个顾客、每个废品处理中心和停车场都有时间窗约束,车辆只能在规定的时间段内为顾客服务、到达废品处理中心清空废品和从停车场出发并返回。
(2)每个司机在上午11点到下午1点的时间段内有1h的午餐休息时间。
(3)每辆车的最大容量为Q,且所有车的类型相同。
(4)每辆车每天能够访问的最大顾客总数为R,每天能够收集的最大废品总质量为mW。
(5)每辆车可多次到废品处理中心清空废品,最后空车返回停车场。
(6)顾客i有质量为Wi的废品要收集,每辆车在每个顾客点收集废品或在废品处理中心清空废品所用的时间为ti。
(7)每个顾客有且只能被访问一次。
1.2模型的建立
本模型的优化目标是最小化所有车辆的总燃油消耗,主要考虑车辆载重和运输距离对燃油消耗的影响。在i、j两点之间运输时,车辆每千米的燃油消耗ρi j与车辆载重Li k的函数关系使用Xiao等[4]提出的计算方法,最小化所有车辆的总燃油消耗为
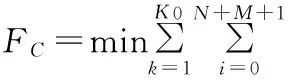
(1)
约束为
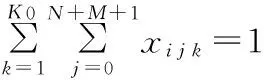
(2)
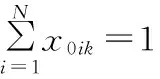
(3)
Li k≤Q∀k∈K,i∈{1,2,…,N,N+M+1}
(4)
Li k=0∀k∈K,i∈{0,N+1,N+2,…,N+M}
(5)
Li k+Wj-Lj k≤(1-xi j k)MB
(6)
∀k∈K,i,j∈{0,1,…,N+M+1}
式中,MB为大常数。
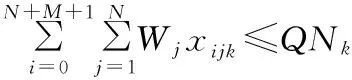
(7)
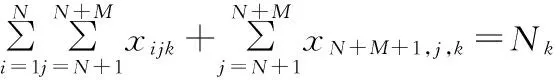
(8)
(9)
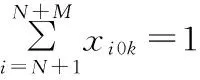
(10)
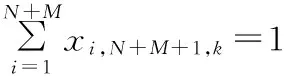
(11)
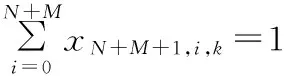
(12)
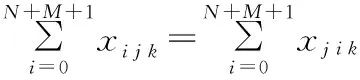
j∈{0,1,…,N+M+1}
(13)
Ti k+ti+di j/vS-Tj k≤(1-xi j k)MB
∀k∈K,(i,j)∈A
(14)
Ti k+ti+tN+M+1+vS-Tj k≤
(2-xi,N+M+1,k-xN+M+1,j,k)MB∀k∈K,(i,j)∈A
(15)
ai≤Ti k≤bi∀k∈K,i∈{0,1,…,N+M+1}
(16)
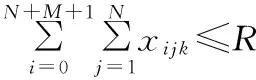
(17)
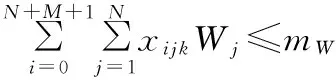
(18)
xijk∈{0,1}∀k∈K,(i,j)∈A
(19)
Nk=0,1,2,…∀k∈K
(20)
Lik≥0∀k∈K,i∈{0,1,…,N+M+1}
(21)
式(2)保证每个顾客有且只能被一辆车服务一次;式(3)保证每辆车都从停车场出发;式(4)保证车辆的载重在收集顾客废品的过程中始终小于车辆的最大载重;式(5)保证车辆离开废品处理中心或从停车场出发时,车辆的载重为0;式(6)表示车辆从一个顾客收集点到下一个顾客收集点时车内废品质量所要满足的约束;式(7)、式(8)保证每天每辆车所收集的废品总质量不超过车辆到废品处理中心的次数所能运输的废品总质量;因为车辆最后要经过废品处理中心返回停车场,所以式(9)保证车辆离开废品处理中心到顾客和午餐休息时间点的次数比车辆到达废品处理中心的次数少1;式(10)保证车辆最后经过废品处理中心返回停车场;式(11)、式(12)保证车辆在每天的运输中,司机都有一个午餐休息时间;式(13)保证车辆到达收集点后必须离开该收集点;式(14)~式(16)是保证顾客、废品处理中心、司机午餐休息时间和停车场的时间窗约束;式(17)保证每辆车访问的最大顾客总数有限;式(18)保证每辆车收集的最大废品总质量有限;式(19)~式(21)是相关变量的非负约束。
2 算法设计
由于最大最小蚁群算法构造的可行解质量直接影响最终算法的整体效果,而最大最小蚁群算法求解大规模废品收集车辆路径问题的质量和效果往往较差,因此,提出一种改进的最大最小蚁群算法,具体的流程如图2所示,针对可行解质量问题,提出一种在最大最小蚁群算法的概率状态转移规则中引入带距离限制的最近邻域搜索的方法,通过此方法构造可行解。
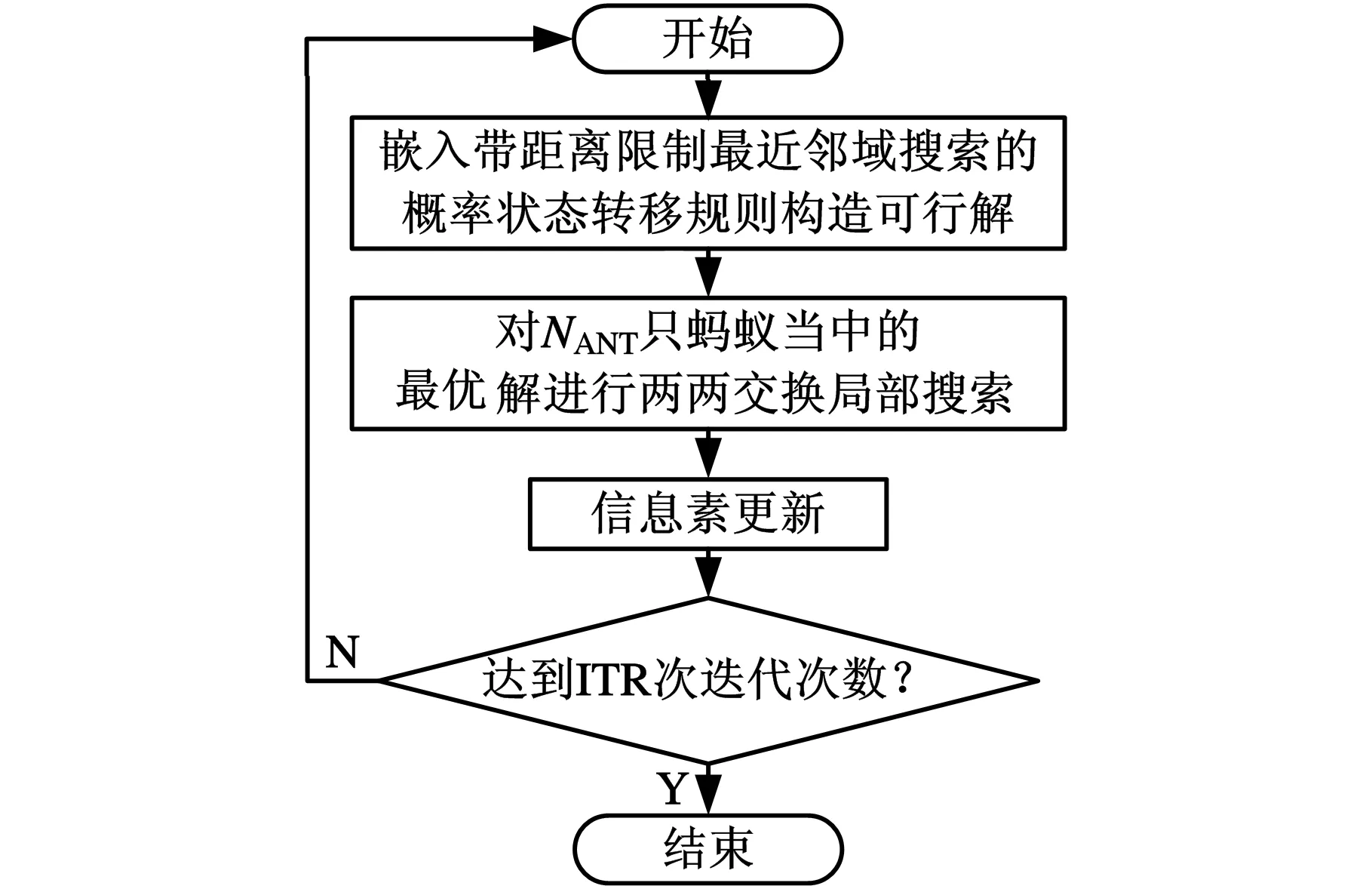
图2 改进最大最小蚁群算法流程图
2.1可行解构造方法
开始时在停车场放置NANT只蚂蚁,每只蚂蚁所走过的完整路径代表该模型的1个可行解,每个可行解可能包含多辆车。每只蚂蚁在构造可行解时,假设停车场有足够的车辆,且1辆车在满足时间窗、总顾客数和总质量等约束范围内完成运输后,接着安排下一辆车从停车场出发到各顾客收集废品,直到所有顾客的废品都收集完毕。每只蚂蚁构造可行解的流程如图3所示。
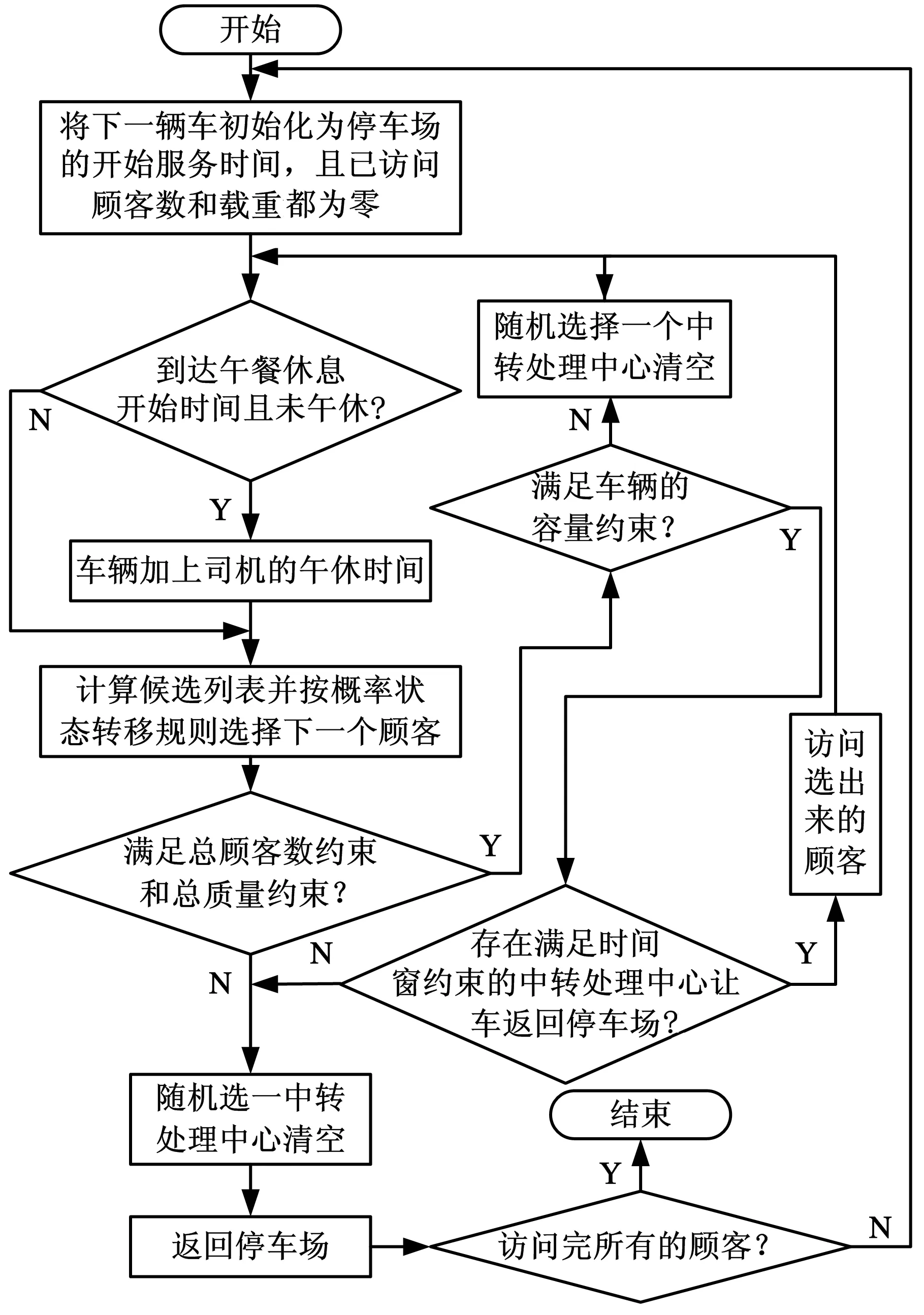
图3 可行解构造流程图
2.1.1满足时间窗约束的动态候选列表
最大最小蚁群算法求解较大数据规模(包含200个以上的顾客)的车辆路径问题时性能仍然会劣化[8-9]。以往,为了优化此问题和提高最大最小蚁群算法的收敛速度,往往将固定数量的距离当前顾客最近的未访问顾客作为当前顾客的候选列表(candidatelist),但难以确定该固定数量的最优值,如Bullnheimer等[10]不管车辆路径问题所包含的总顾客数多大,都将顾客的候选列表(从当前顾客出发,满足约束的下一个顾客的集合)大小设为总顾客数的1/4。
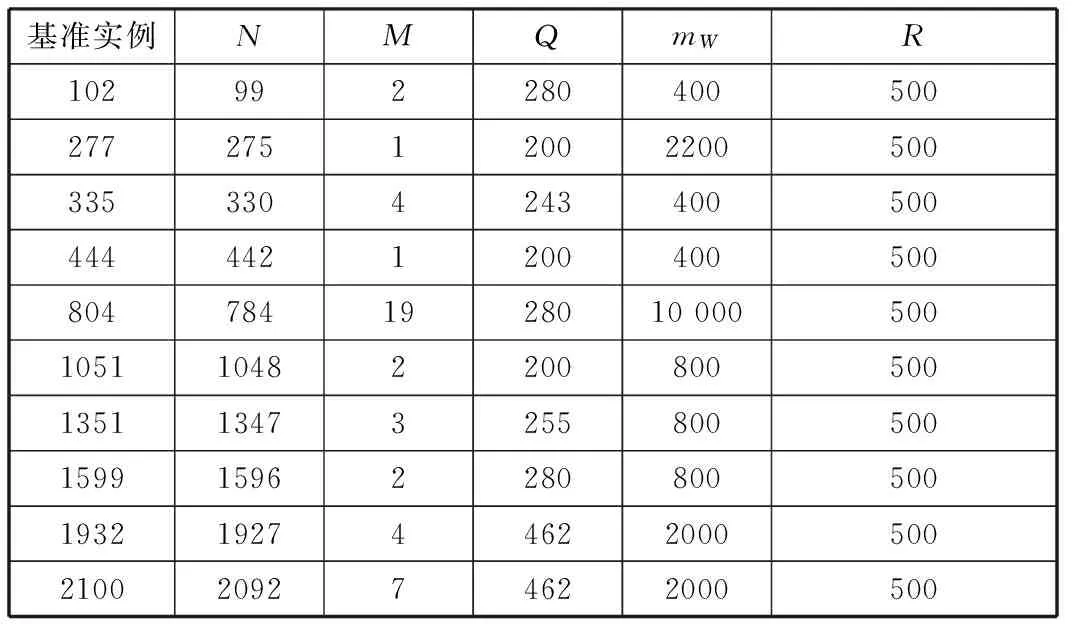
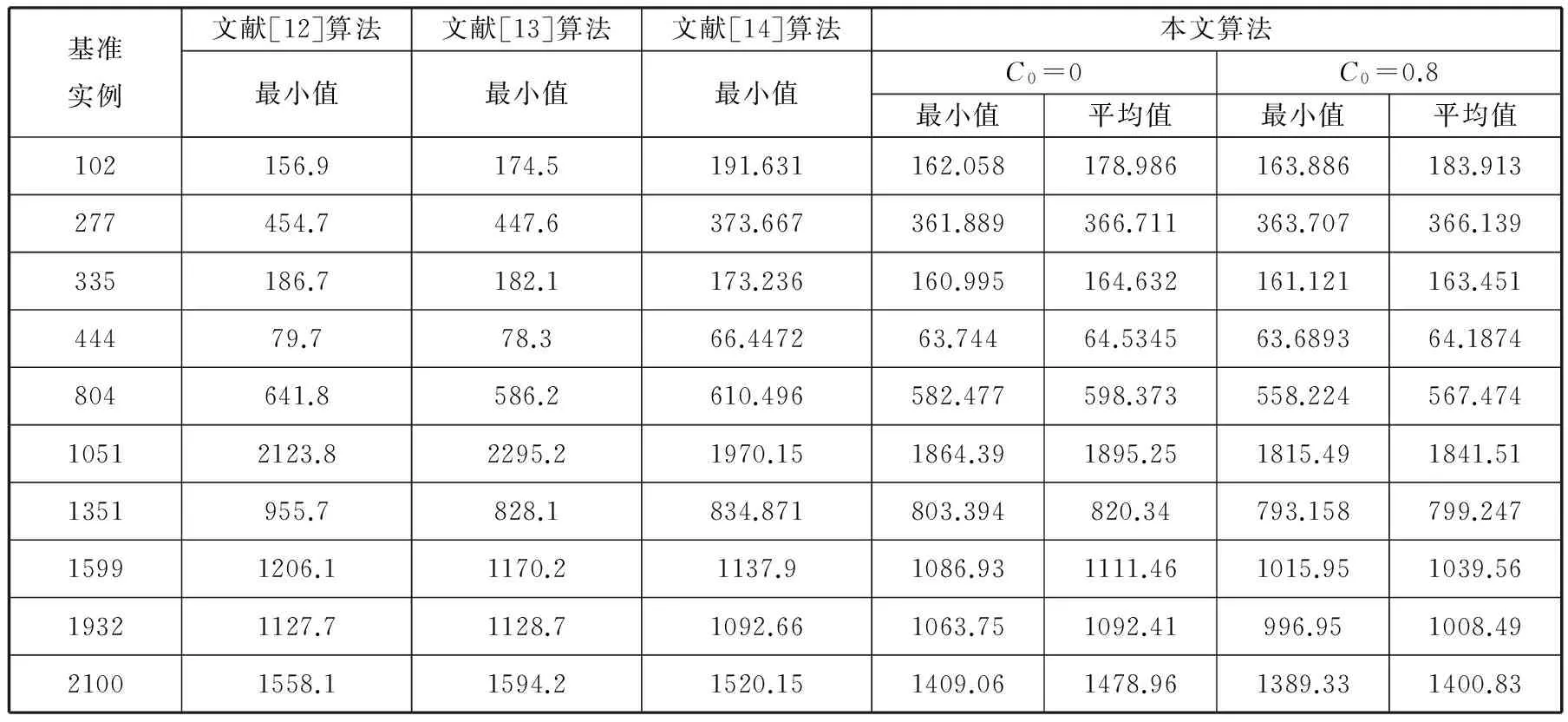
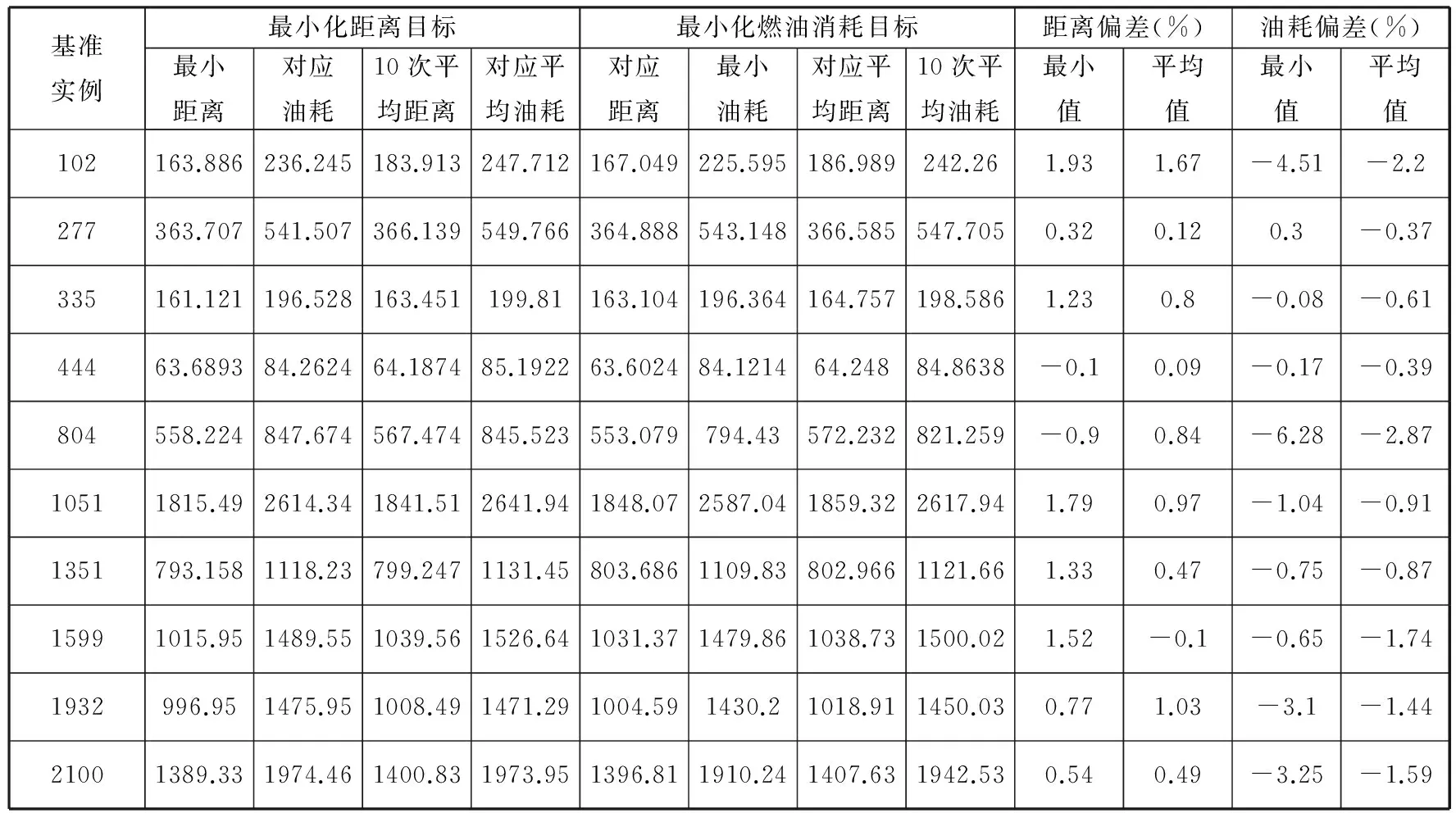
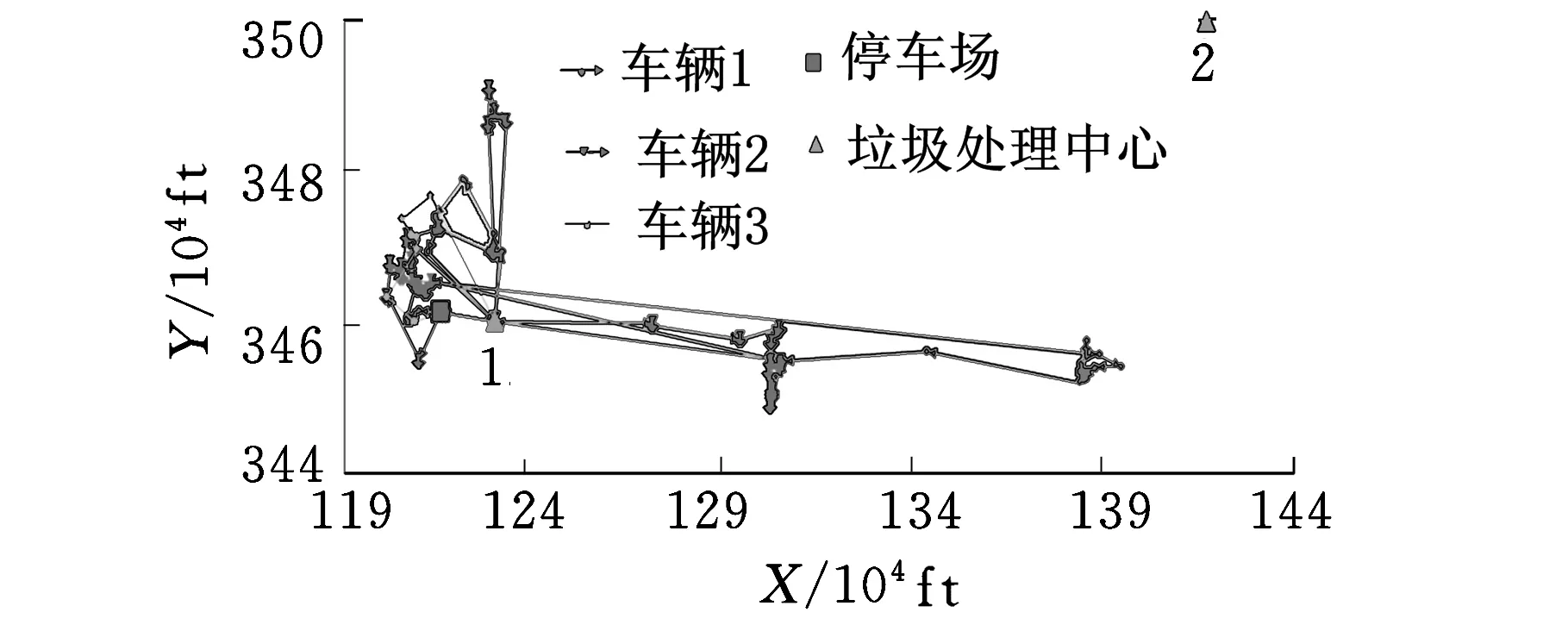
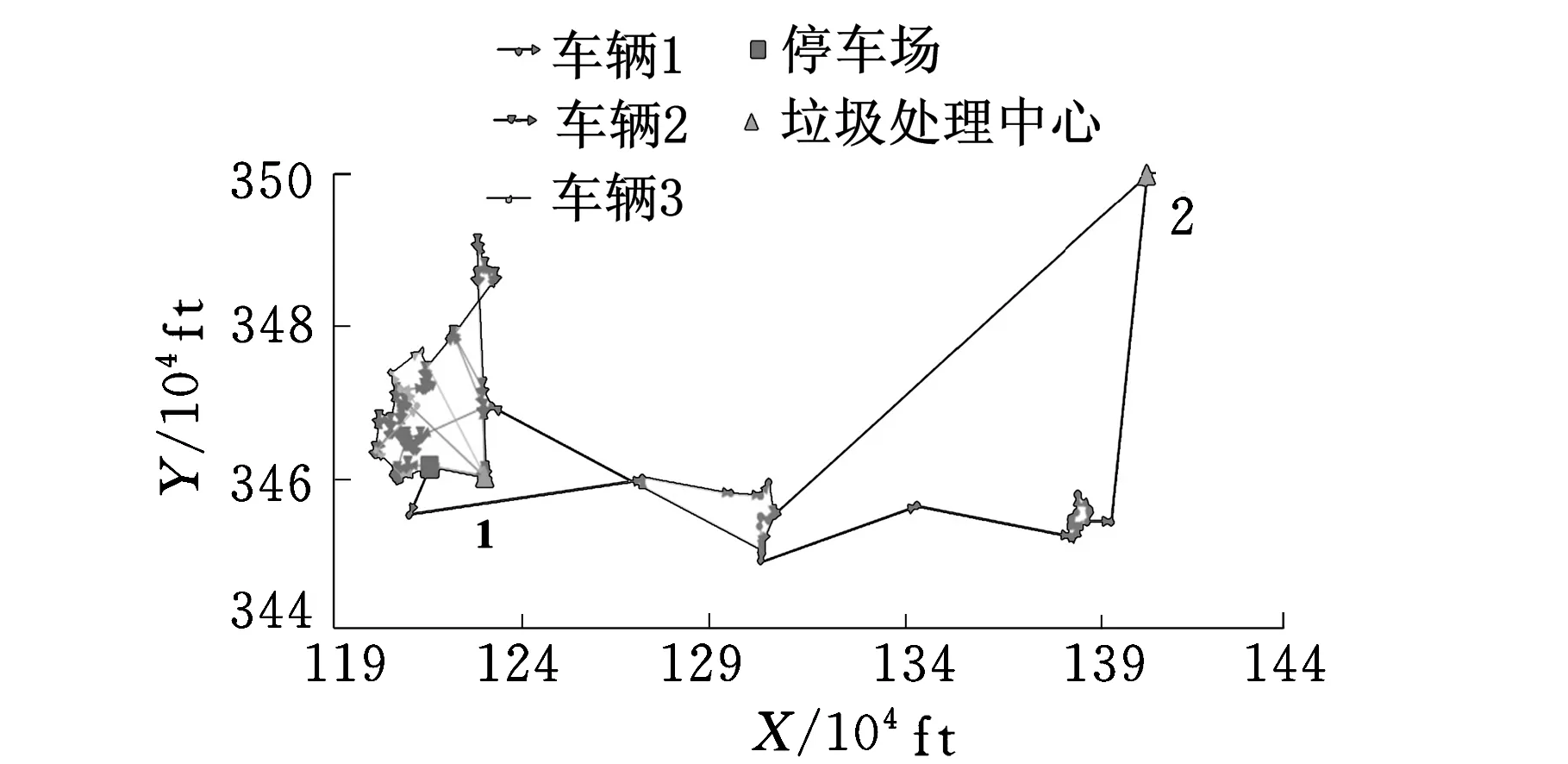
本文考虑的带时间窗废品收集车辆路径问题的总顾客数往往超过2000,将顾客候选列表的大小设为总顾客数的1/4对提高最大最小蚁群算法的收敛速度几乎没有影响。同时,由于选取顾客的候选列表是基于距离最近的规则,在算法的整个过程中,每个顾客的候选列表包含的顾客都是固定的,从而缩小了可行解的范围。因此,针对不同规模车辆路径问题难以确定最优的顾客候选列表大小和采用固定顾客候选列表导致可行解范围缩小的问题,本文设计了满足时间窗约束的优先候选列表和次要候选列表。计算这两类动态候选列表的方法为:假设被访问的当前顾客为顾客i,未被访问的顾客(顾客j)的时间窗为[aj,bj]。若访问顾客i后,车辆从i到达j的时间恰好落在顾客j的时间窗内,即到达顾客j的时间tj满足约束aj≤tj≤bj,则顾客j放入优先候选列表;若访问顾客i后,从i到达j的时间早于顾客j的开始服务时间,即tj 从以上设计可以看到,由于优先候选列表和次要候选列表的划分满足时间窗约束,每个顾客的候选列表的大小可能不一样,并随顾客的访问顺序和各自时间窗的不同而变化,因此与采用固定数量的顾客候选列表的方法相比,这种采用满足时间窗约束的优先候选列表和次要候选列表的划分方法没有丢失可行解。从当前顾客的优先候选列表中选取1个顾客时,车辆无需等待即可为该顾客服务;从次要候选列表中选取1个顾客时,还需等到该顾客的时间窗开始才能服务。因此,为了尽可能减少车辆的等待时间,从当前顾客的候选列表中选择下一个要访问的顾客时,优先从优先顾客候选列表中选择,只有当优先候选列表为空时,才从次要候选列表中选取下一个顾客。 2.1.2带距离限制最近邻域搜索的概率状态转移 为了克服最大最小蚁群算法收敛速度慢的缺点,本文在Stützle等[7]所提最大最小蚁群算法所采用的从当前顾客的候选列表中随机选取下一个顾客j的概率状态转移规则中,引入带距离限制的最近邻域搜索,新的概率状态转移规则为 (22) (23) (24) η(i,j)=1/dij(i,j)∈A且i≠j 其中,arg()函数表示满足arg括号内约束时的定义域内的值;Tk(i)为第k只蚂蚁在当前顾客i时可选择的满足时间窗约束的下一个顾客的候选列表;div为顾客i与下一个顾客(顾客v)之间的距离;τ(i,v)为顾客i与顾客v之间的路径上的信息素;η(i,v)为顾客i与顾客v之间路径上的启发式信息;α、β为常数;J表示满足约束C0 C≤C0时,采取最近邻域搜索选取下一个要访问的顾客。为了解决最近邻域搜索的过度贪心导致收敛到次优解的缺点,将所有顾客两两之间距离的算数平均值d作为最近邻域搜索的最大搜索半径。采用所有顾客两两之间距离的算数平均值d作为最近邻域搜索的最大搜索半径获取下一个顾客的具体方法为:从满足时间窗约束的优先候选列表或次要候选列表中筛选出与当前顾客的距离小于d,且与当前顾客距离最近的顾客作为下一个要访问的顾客。如图4所示,假如产生的随机数C≤C0,则从以当前顾客为圆心、以d为半径的圆内选取离当前顾客最近,且满足时间窗约束的顾客点1进行访问。C0 图4 概率状态转移规则示意图 2.2两两交换局部搜索 制定嵌入带距离限制最近邻域搜索的概率状态转移规则,当NANT只蚂蚁按照此规则构造出可行解后,为了提高最终解的质量,对构造出最优解的那只蚂蚁的路径进行两两交换局部搜索。为减少算法的运行时间,只对最好解中每条车辆路径的顾客或者废品处理中心进行交换,不进行不同车辆路径之间的顾客或者废品处理中心的交换,具体步骤如下。 (1)设SS0为NANT只蚂蚁所构造出来解中的最优解,FD0为其对应的目标函数值,设k=1表示SS0中的第一辆车,所访问的顾客和废品处理中心总数为vn k,该车访问的第一个顾客为i,假设i=1,下一个顾客或者废品处理中心j=i+1=2,令变量SS*=SS0,SS*对应的目标函数值FD*=FD0。 (2)若i (3)j (4)i=vn k时,对可行解SS0中第k辆车的局部搜索完毕,令k←k+1,j=i+1,i=1,j=i+1=2,然后对解SS*中下一辆车的路径执行步骤(2)和步骤(3),直到可行解SS0中所有车辆路径都进行了局部搜索,输出SS*和FD*。 2.3信息素更新 在最大最小蚁群算法中,只允许在迭代最优路径或全局最优路径上遗留信息素。为了防止算法过早收敛,限制路径上的信息素在[τmin,τmax]范围内,并在算法开始时将所有路径上的信息素初始化为信息素最大值τmax以增加算法的探索能力[9]。本文选择在迭代最优路径SS*上遗留信息素,即有 τi j(t+1)=τi j(t)+1/FD* (25) 然后对所有路径按下式进行信息素的蒸发: τi j(t+1)=(1-ρ)τi j(t) (26) 最后检查所有路径上的信息素是否在[τmin,τmax]范围内,若不是则调整到相应的信息素最小值τmin或最大值τmax。在算法开始时将所有路径上的信息素初始化为信息素最大值τmax=τ0,τ0按下式计算: τ0=1/(ρCn n) (27) 其中,Cn n为使用最近邻域搜索获得的目标函数值,信息素最小值τmin采用下式进行计算: τmin=τmax/(2M+2N) (28) 每次迭代后,对信息素的限制范围[τmin,τmax]进行更新,τmax采用下式进行计算: τmax=1/(ρFD*) (29) τmin仍然按式(28)计算。 3.1运输距离最小的基准实例测试 为了说明在求解大规模废品收集车辆路径问题时在最大最小蚁群算法中嵌入带距离限制的最近邻域搜索的有效性,将所提出的改进最大最小蚁群算法用于求解Kim等[9]针对带有时间窗、司机休息时间以及多个中转废品处理中心的废品收集车辆路径问题模型所设计的10个基准实例。为了便于比较,统一以车辆运输距离最小为优化目标。具体的基准实例如表2所示,其中,基准实例中的数字表示废品收集车辆路径问题中顾客废品收集点、中转站和停车场的总数。 表2 问题基准实例 本算法采用C++编程实现,试验次数为10,具体结果如表3所示,其中,C0=0表示没有使用最近邻域搜索,C0=0.8表示使用了带有距离限制的最近邻域搜索。其他参数都相同,分别为α=1,β=2,ρ=0.2,Q0=0.9,蚁数NANT=20,迭代次数为50。将上述结果与3种以最小化车辆运输距离为优化目标的求解该基准实例的效果较好算法(Benjamin等[10]采用的禁忌搜索和变邻域搜索的混合算法、Buhrkal等[11]所采用的自适应大规模邻域搜索算法和Islam等[12]采用的蚁群算法)进行比较,结果如表3所示。 从表3可以看出,对于小数据规模废品收集车辆路径问题,如实例102和277,本文提出的算法没有显著优越性。对于废品收集点个数达到804以上的大规模废品收集车辆路径问题,嵌入带距离限制的最近邻域搜索的最大最小蚁群算法的效果明显要好,如实例1932所示,这说明通过在最大最小蚁群算法中嵌入带距离限制的最近邻域搜索,能够在求解大规模的废品收集车辆路径问题时实现对算法的改进。同时,与其他3种算法相比,本文提出的带距离限制的最近邻域搜索的最大最小蚁群算法在10个基准实例中获得了9个更好解,从而验证了该算法在求解大规模废品收集车辆路径问题的有效性。 3.2最小化距离和油耗的实例测试 为了验证本文提出的考虑车辆载重和距离对车辆燃油消耗的影响的情况下所得最小化燃油消耗优化目标的有效性,分别以最小化距离和最小化燃油消耗为优化目标,将所设计的带距离限制的最近邻域搜索的最大最小蚁群算法用于求解表2中的基准实例,结果如表4所示。计算过程相关参数设置如下:ρ*=2,ρ0=1,C0=0.8,其他参数如3.1节所述。为了更直观地说明两种优化目标对距离和油耗的影响,采用下式计算两种优化目标情况下的距离偏差和油耗偏差: 表3 与其他文献得到的距离最小值比较 miles 表4 两种优化目标的结果比较 (31) 其中,φ为偏差;Fρmin为最小化燃油消耗目标的对应值;Fdmin为最小化距离目标的对应值。 由表4可以看出,10次结果中的平均值情况是,最小化油耗目标得出的油耗都低于最小化距离目标得到的油耗;最小值情况下,除实例277外也是最小化油耗目标得出的油耗都低于最小化距离目标得到的油耗。这说明单纯以最小化距离为优化目标进行路径优化并不能得到最小的燃油消耗,同时以燃油消耗为优化目标尽管在运输距离上可能有所增加但可以有效降低总油耗,验证了本文所提最小化燃油消耗优化目标的有效性。 图5 最小化距离目标下102实例的车辆路径示意图 图6 最小化燃油消耗目标下102实例的车辆路径示意图 为了进一步说明最小化燃油消耗优化目标的重要性,将最小化距离为优化目标所得的距离最小值对应的车辆路径和以最小化燃油消耗为优化目标所得油耗最小值对应的车辆路径画出,如图5、图6所示,限于篇幅,仅画出102实例。从图5、图6可以看出,最小化距离和最小化燃油消耗为优化目标所得到的车辆路径大不相同,且最小化距离目标的车辆路径中只用到了中转废品处理中心1;最小化燃油消耗目标的车辆路径中,中转废品处理中心1、2都用到了。因此,如果只从最小化距离目标的角度来看,中转废品处理中心2是无需设置的,但从最小化燃油消耗的角度来看,中转废品处理中心2的设置可以有效减少燃油消耗。由此可见,以最小化燃油消耗为目标进行优化不仅会改变车辆访问废品收集点的顺序从而节省油耗,而且还可能影响到设施规划等其他相关决策的制定和实施。 为了研究车辆载重和距离这两个因素对带有时间窗和多个中转废品处理中心的废品收集车辆路径问题中燃油消耗的影响,本文在考虑车辆载重和距离对燃油消耗影响的情况下,建立了带有时间窗、司机休息时间以及多个中转废品处理中心的最小化燃油消耗的废品收集车辆路径问题模型。针对废品收集车辆路径问题数据规模大的特点,设计了一种改进的最大最小蚁群算法进行求解,对基准实例的测试证明了所提优化目标和算法的有效性。 由于车辆的燃油消耗不仅与车辆行驶路程和车辆载重有关,还与车辆行驶速度等因素有关,而本研究假设车辆行驶速度恒定,因此,后续研究可进一步考虑车辆行驶速度、载重、车辆运输距离等多因素作用下的废品收集车辆路径问题中的燃油消耗问题。 [1]Sahoo S,Kim S,Kim B I,et al.Routing Optimization for Waste Management[J].Interfaces,2005,35(1):24-36. [2]Angelelli E,Speranza M G.The Application of a Vehicle Routing Model to a Waste-collection Problem:Two Case Studies[J].The Journal of the Operational Research Society,2002,53(9):944-952. [3]Baldacci R,Hadjiconstantionou E,Mingozzi A.An Exact Algorithm for the Capacitated Vehicle Routing Problem Based on a Two-commodity Network Flow Formulation[J].Operations Research,2004,52(5):723-738. [4]Xiao Y,Zhao Q,Kaku I,et al.Development of a Fuel Consumption Optimization Model for the Capacitated Vehicle Routing Problem[J].Computers & Operations Research,2012,39(7):1419-1431. [5]Tavares G,Zdena Z,Viriato S,et al.A Case Study of Fuel Savings through Optimization of MSW Transportation Routes[J].Management of Environmental Quality:An International Journal,2008,19(4):444-454. [6]Zsigraiova Z,Semiao V,Beijoco F.Operation Costs and Pollutant Emissions Reduction by Definition of New Collection Scheduling and Optimization of MSW Collection Routes Using GIS.The Case Study of Barreiro,Portugal[J].Waste Management,2013,33(4):793-806. [7]Stützle T,Hoos H.The Max-min Ant System and Local Search for Combinatorial Optimization Problems[C]//1997 IEEE International Conference on Evolutionary Computation.Indianapolis,1997:309-314. [8]Bullnheimer B,Hartl R F,Strauss C.An Improved Ant System Algorithm for the Vehicle Routing Problem[J].Annals of Operations Research,1999,89:319-328. [9]Kim B I,Kim S,Sahoo S.Waste Collection Vehicle Routing Problem with Time Windows[J].Computers & Operations Research,2006,33(12):3624-3642. [10]Benjamin A M,Beasley J E.Metaheuristics with Disposal Facility Positioning for the Waste Collection VRP with Time Windows[J].Optimization Letters,2013,7(7):1433-1449. [11]Buhrkal K,Larsen A,Ropke S.The Waste Collection Vehicle Routing Problem with Time Windows in a City Logistics Context[J].Procedia Social and Behavioral Sciences,2012,39:241-254. [12]Islam R,Rahman M S.An Ant Colony Optimization Algorithm for Waste Collection Vehicle Routing with Time Windows,Driver Rest Period and Multiple Disposal Facilities[C]//2012 International Conference on Informatics,Electronics & Vision.Dhaka,2012:774-779. (编辑张洋) Waste Collection Vehicle Routing Problem with Time Windows Based on Improved Ant Colony Optimization Liu QiongLiu XiuchengZhang ChaoyongRao Yunqing State Key Laboratory of Digital Manufacturing Equipment & Technology,Huazhong University of Science and Technology,Wuhan,430074 A mathematical model aiming at minimizing the fuel consumption for the waste collection vehicle routing problem with time windows,driver rest period and multiple disposal facilities was set up.The main factors to affect the fuel consumption of a vehicle considered herein were the load of a vehicle and distance traveled.An improved MAX-MIN ant system algorithm was proposed.Based on characteristics of the time windows,two kinds of dynamic candidate lists were designed to improve the searching efficiency of the algorithm.A new probabilistic condition transition rule for the MAX-MIN ant system algorithm was proposed.The nearest neighborhood search with distance limitation was integrated in the transition rule of proposed algorithm.The proposed model and algorithm were validated by comparion with benchmark problems in literatures. large scale vehicle with time windows;routing problem;ant colony optimization;fuel consumption 2013-10-08 国家自然科学基金资助重点项目(51035001);国家自然科学基金资助项目(51275190);国家科技重大专项(2011ZX04015-011-07);中央高校基本科研业务费专项资金资助项目(HUST:2013ZZGH002) TP391< class="emphasis_italic">DOI :10.3969/j.issn.1004-132X.2015.02.022 刘琼,女,1965年生。华中科技大学数字制造装备与技术国家重点实验室教授、博士。主要研究方向为物流系统管理、制造系统集成优化。刘秀城,男,1989年生。华中科技大学数字制造装备与技术国家重点实验室硕士研究生。张超勇,男,1972年生。华中科技大学数字制造装备与技术国家重点实验室副教授、博士。饶运清,男,1968年生。华中科技大学数字制造装备与技术国家重点实验室教授、博士。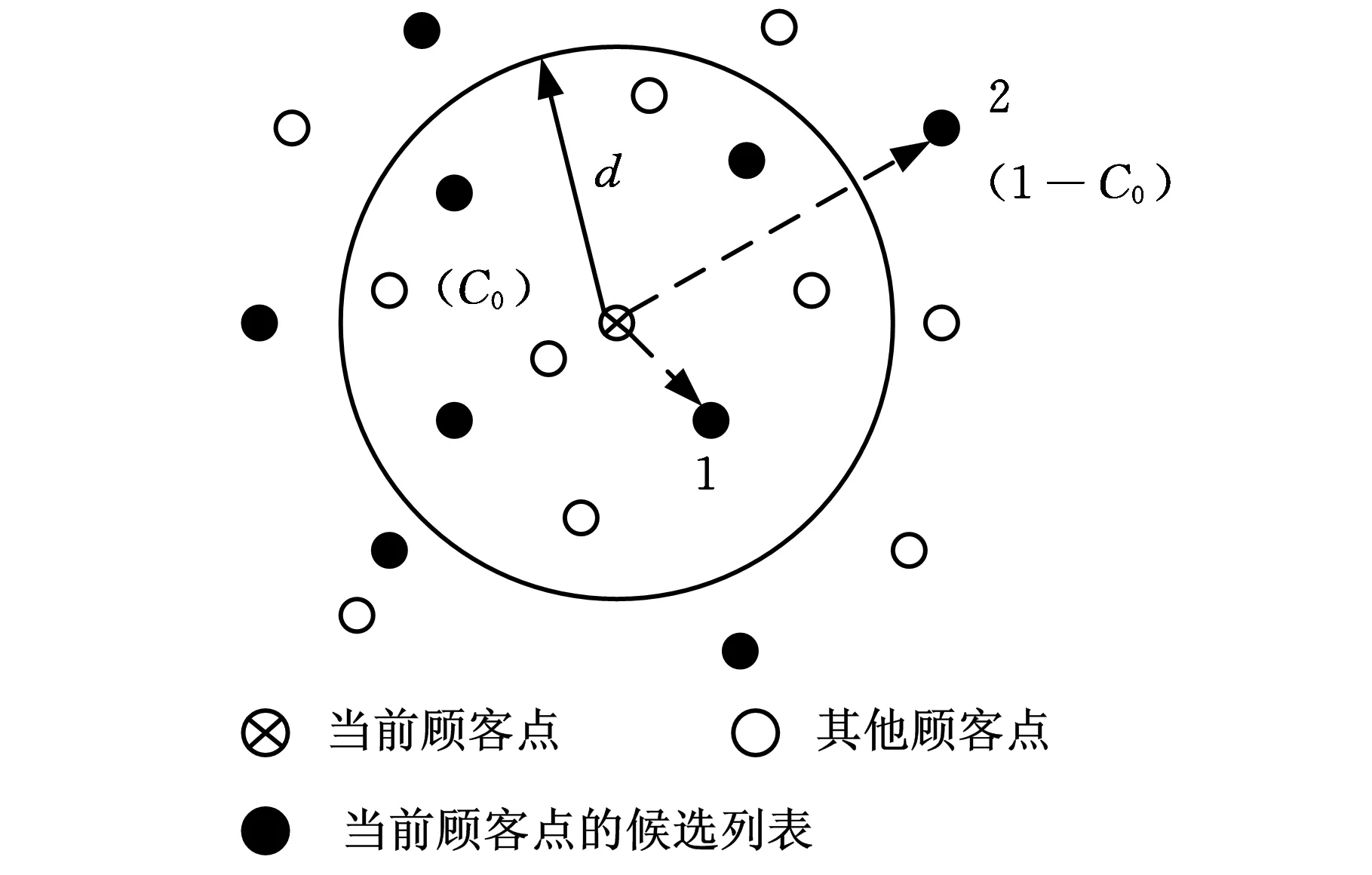
3 实验结果与分析
4 结语

