随机风速下风力发电机组载荷传递特性研究

王　洋　孙　伟　魏　静　李　想　胡兴龙

大连理工大学,大连,110624

随机风速下风力发电机组载荷传递特性研究

王洋孙伟魏静李想胡兴龙

大连理工大学,大连,110624

选取指数律函数描述平均风速,运用基于自回归模型的线性滤波法建立的风速模型模拟自然界随机风速。根据动量矩定理和简单的弹簧-质量-阻尼模型建立风力发电机组传动系统刚性传动模型及柔性传动模型来描述系统动态特性。以5 MW变速变桨距风力发电机组参数为依据，计算随机风速下两种不同传动模型对风轮叶片以及发电机转子的动态响应的影响，并对结果进行对比分析。基于柔性传动模型，研究不同主轴刚度对传动系统动态响应的影响，得出最佳主轴刚度，并利用雨流计数法描述不同主轴刚度下风力发电机组传动系统的动态响应。研究结果可为风力发电机组传动系统动态特性的研究提供载荷数据。

AR模型;传动系统;载荷传递;雨流计数

0　引言

风力发电机工作环境恶劣，体积庞大，不便于吊装维护，因此对其寿命和可靠性提出了很高的要求。外部载荷变化是导致风力发电机传动系统部件疲劳破坏的直接原因，因此，近年来研究时变外载下风电传动系统的动态特性得到了越来越多的关注。

文献[1]运用ADAMS,针对750 kW风力发电机齿轮箱传动系统故障,建立虚拟样机进行了动力学分析。文献[2]利用ANSYS有限元软件,对正常运行和危险工况下的低风速风力发电机轮毂进行有限元分析,得到了轮毂的应力分布。文献[1-2]都是在额定风速下对风电传动系统部件进行可靠性分析的,没有考虑风速的变化。文献[3]以300 kW变转速水平轴风力发电机为分析对象，对其动态模型在紊流风场下进行了仿真计算。文献[4]研究了变转速风力发电机整个运行过程的仿真分析方法。文献[3-4]虽然考虑了风速的变化,但对风速的处理较简单,未考虑风速变化的随机性。文献[5]采用变风速下风力发电机齿轮传动系统的时变输入转矩作为外部激励，建立了风力发电机齿轮传动系统的耦合动力学模型，求解了风力发电机齿轮传动系统的动态特性。文献[6]建立了风力发电机传动系统在随机风速下的载荷模型,利用该模型对风力发电机进行了实例计算，得到了传动系统的随机载荷。文献[5-6]都建立了随机风速模型，研究其对传动系统的影响，但没有考虑主轴以及高速轴的柔性对传动系统传递特性的影响。

本文利用AR法构建随机风速模型,以5 MW变速变桨距风力发电机组参数为依据，研究随机风速下刚性传动系统模型和柔性传动系统模型对系统动态响应的影响，以及主轴刚度对传动系统的影响，为风力发电机组传动系统动态特性的研究提供可靠载荷数据。

1　随机风速的模拟

自然风是风电传动系统输入端的决定因素，因此模拟风速使其尽可能接近自然风特性，对风电传动系统动态特性研究的准确性具有重要意义。大量实测记录表明，风速可看作平均风速和脉动风速两部分组成。

1.1平均风速

大气边界层内平均风速的变化常用对数或指数函数来表达,分别如下[7]:

(1)

(2)

指数律比对数律计算简便，且两者差别不明显，因此选用指数律函数描述平均风速。

1.2AR脉动时程

当前,国内外对风速时程进行数值模拟的主要方法有谐波叠加法和线性滤波法。线性滤波法计算速度快，且可考虑时间相关性，近年来得到广泛的应用。常用的线性滤波法有AR自回归模型、MA滑动平均模型及ARMA自回归滑动平均模型。大量文献研究认为，阶数对于结果的影响很小，因此本文选用AR模型模拟脉动风速时程。

M个点空间相关脉动风速时程的AR模型可参照文献[8],该模型表示：某时刻风速等于之前各时刻风速的线性组合加上一个独立随机过程向量。

根据目前现有对脉动风速时程的模拟进行描述的文献可知,模拟脉动风速的关键在于自谱密度函数的选取。脉动风速功率谱主要反映脉动风中各种频率成分对应的能量分布规律,按是否考虑湍流积分尺度随高度的变化分两大类：一类是不考虑湍流积分尺度随高度的变化，如Davenport谱、Harris谱，另一类是考虑湍流积分尺度随高度的变化,如Kaimal谱、von Karman谱。由于MW级风电发电机的轮毂比较高,因此本文采用考虑随高度变化影响的脉动风速功率谱von Karman谱,其表达式如下：

(3)

式中,f为频率;σ为速度标准差;L为湍流尺度参数;vhub为轮毂处的平均风速。

2　变速变桨风机功率调节原理

风机组吸收风能风轮产生的输出功率为[8]

(4)

式中,CP为风能利用系数;ρ为空气密度;A为叶片扫略面积;v为风速。

在一定风速下,ρ、A都是常量,因此产生功率的大小取决于风能利用系数CP。对于变速变距运行的风力发电机来说,CP是叶尖速比λ和桨距角β的函数。风能利用系数可近似用下式来表示[8]:

(5)

λ=wR/v

式中，R为风机叶片的半径;w为风轮的转动角速度。

图1所示为风能利用系数与叶尖速比、桨距角的关系。可以看出,对于每一确定的桨距角都有一个最佳叶尖速比使得风能利用系数最大。

图1　风能利用系数与叶尖速比、桨距角的关系

变速变桨风电机组运行原理如下:在低风速时，桨距角不变，通过调节发电机转矩使风轮按照最佳叶尖速比运行，追踪最佳风能利用系数，充分利用风能;在高风速时,通过变桨距角限制气动力矩，使功率稳定输出；当风速超出切出风速时,系统会进行紧急制动，即调节叶片为顺桨状态，叶轮不接收风能，刹车闸闭合，提供恒定的制动扭矩，发电机脱离电网，保证风力发电机的安全，在制动扭矩的作用下,系统传动轴做匀减速运动，直至叶片速度为0。具体表达式如下：

(6)

(7)

式中,nG为发电机转子转速;ne为发电机转子额定转速;TG为发电机电磁转矩;Te为发电机额定电磁转矩;vin为切入风速;ve为额定风速;vof f为切出风速。

3　传动模型的建立

3.1刚性传动模型

传动系统主要由风轮转子、主轴、齿轮箱、高速轴、刹车闸和发电机转子构成。风轮转子的加速度由气动转矩和主轴转矩之间的不平衡产生。发电机转子的加速度由高速轴扭矩和发电机转子转矩之间的不平衡产生。刚性传动链不考虑主轴的柔性，由于齿轮箱传动轴的转动惯量比发电机转子的转动惯量小得多，对整个系统没有太大的动态影响,因此不考虑它的动态特性,从而建立刚性传动链模型如下[3]:

(8)

式中,JR为风轮转子转动惯量;JG为发电机转子转动惯量;θR为风轮转子角位移;θG为发电机转子角位移;T1为齿轮箱输入转矩;TR为风轮转子转矩;N为齿轮箱传动比。

整理式(8)得

(9)

3.2柔性传动模型

柔性传动链需要考虑主轴及高速轴的柔性,利用弹簧-质量-阻尼模型来描述传递系统动态特性。因主轴的长度较长,其柔性对系统有较大影响，而高速轴由于其轴的长度较短，其柔性对系统的影响较小，此处忽略不计,即此处只考虑主轴的柔性,故柔性传动模型如下[3]:

(10)

式中,θ1为齿轮箱输入角位移;θ2为齿轮箱输出角位移;T2为齿轮箱输出转矩;K1为主轴刚度;B1为主轴阻尼;B2为输出轴阻尼。

因阻尼数量级较小,从而带来的影响很小,所以本文不考虑阻尼的影响,取B1=0。整理式(10)得

(11)

4　随机风速下的载荷传递特性

4.1变风载下齿轮传动系统的载荷传递结果

应用所建立的随机风速和柔性传动模型,依据变速变桨风力发电机组的功率调节特性,根据某5MW风力发电机的物理参数(表1)，仿真计算出传动系统在50s内正常运行的时变载荷,仿真结果如图2所示。

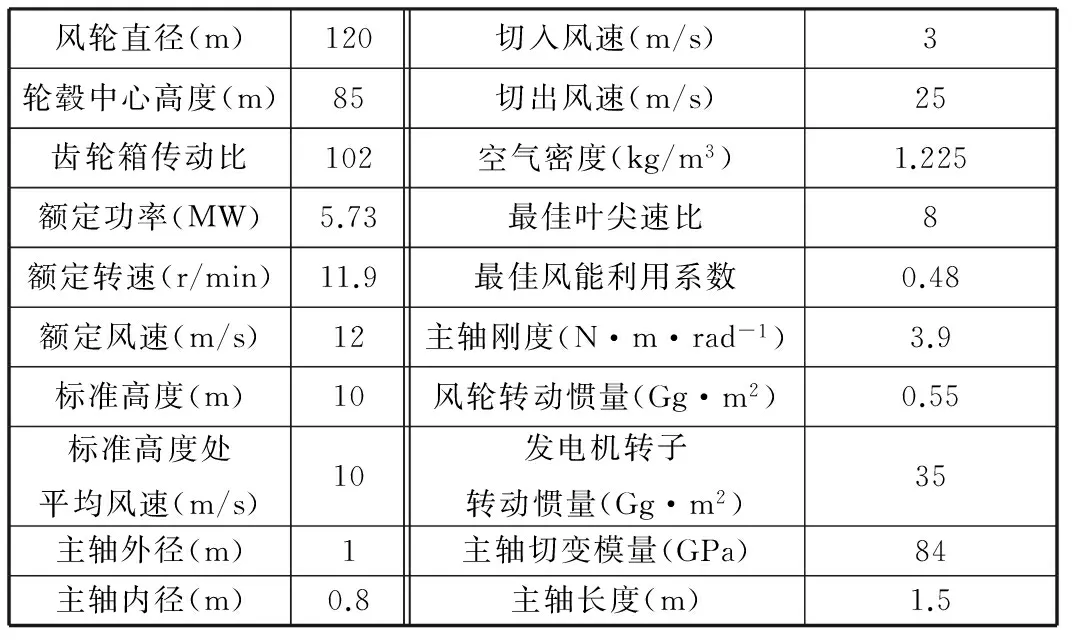
表1　风力发电机组的物理参数

von Karman谱与自然界中的实测风速谱较为吻合[9-10],从图2a中看出,AR模型仿真出的风速序列功率谱与von Karman谱的趋势基本一致,因此可认为AR模型较为真实地反应了自然风的特性，在此时变风速下，风力发电机传动系统载荷传递特性的研究能够很好地反映实际运行情况。从图2d～图2e中看出,叶片转子以及发电机转子动态响应变化趋势与时变风速基本相同，当风速超出额定风速时，系统运行在额定状态。

(a)功率谱

(b)风速

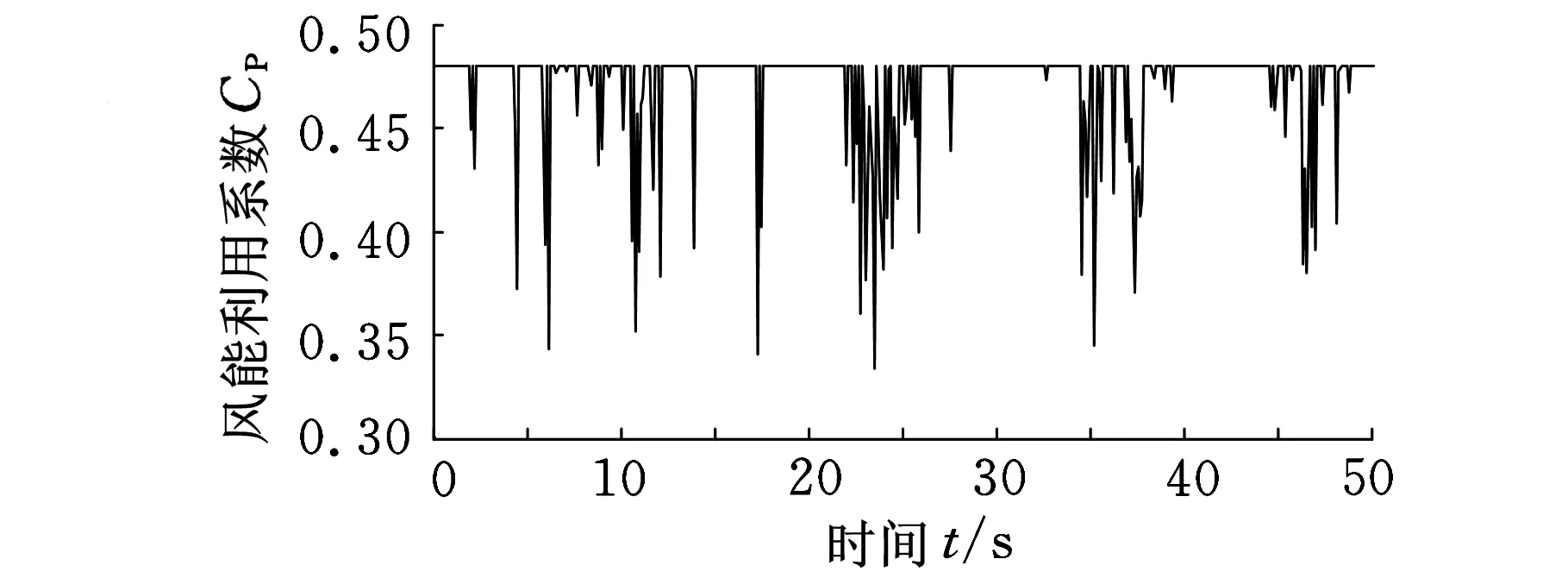
(c)风能利用系数

(d)叶片转子转矩

(e)发电机电磁转矩图2　仿真计算结果

4.2刚性和柔性传动模型载荷传递的结果对比

柔性传动链考虑主轴的柔性,主轴输入端与主轴输出端的角位移响应曲线如图3所示。

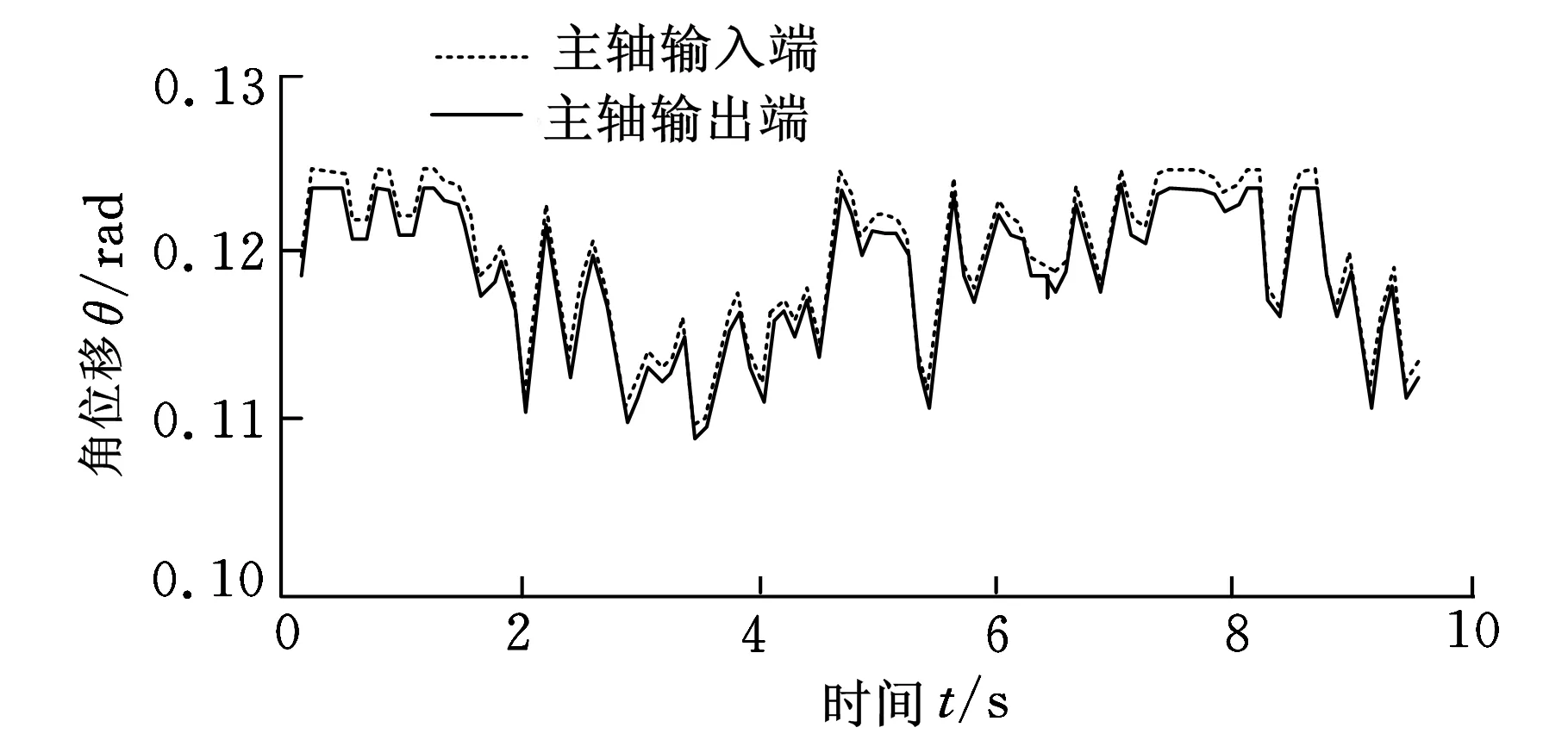
图3　主轴输入端与输出端角位移响应曲线

如图3所示,由于考虑了主轴的柔性,因此其输入端与输出端的角位移值不相同,输入端角位移值大于输出端角位移值,但随时间的变化趋势相同。

分别在刚性和柔性传动链模型下,模拟载荷的传递特性,其结果对比如图4所示。

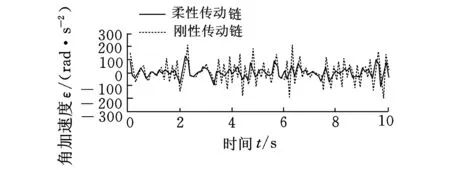
图4　两种传动链下发电机转子动态响应结果对比

角加速度响应可以反映外载对系统的冲击作用,从图4可以看出，两种传动链下，发电机转子角加速度和电磁转矩的变化趋势基本是一致的，但相比之下，柔性传动链减少了外载对传动系统的冲击。柔性传动模型考虑了主轴的扭转变形，更符合实际情况，因此为保证结果的准确性，在研究中应采用柔性传动模型做进一步分析。

4.3主轴刚度对载荷传递的影响

柔性传动模型考虑主轴和高速轴的柔性，与刚性传动模型相比，可以降低外载对系统的冲击，因此研究主轴刚度对传动系统动态响应的影响对风电传动系统的稳定性具有重要意义。

圆轴的扭转刚度公式如下[12]：

(12)

式中,G为切变模量;IP为极惯性矩;L为轴长度;T为扭矩;φ为扭转角;GIP为扭转刚度;GIP/L为单位长度扭转刚度,在本文研究中简称为主轴刚度。

从式(12)可以看出,在主轴材料、内径和外径确定的情况下,影响主轴刚度的因素为主轴的长度L,因此选取主轴长度作为自变量来研究相同变风载下主轴长度对风机传动系统动态响应的影响。在0.625～6 m的范围内选取50个不同数值作为主轴长度，其对应的主轴刚度为0.8～8 GN·m/rad。根据柔性传动模型进行计算，得到50组发电机转子角加速度的动态响应。进而绘制不同主轴刚度下,发电机转子角加速度的最大振幅的变化曲线，如图5所示。

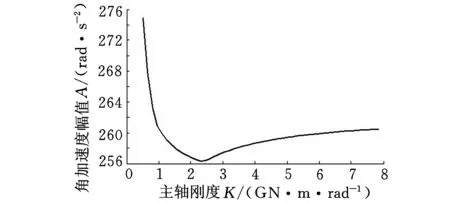
图5　主轴刚度对动态响应的影响变化曲线

从图5中可以看出,随着主轴刚度的降低，冲击先减小后增大，因此可以得出结论：适当地降低主轴刚度可以有效地减少外载对系统的冲击作用，但过小的话，反而降低了系统的稳定性，影响系统寿命。图5所示的对系统冲击最小的主轴刚度为2.3 GN·m/rad,对应的主轴长度为2.17 m。

5　结论

(1)对于大型风力发电机动态响应的研究,应考虑风速随时间和空间的变化,使系统外部激励尽可能接近自然风的特性。

(2)不同载荷传递模型不会影响载荷的变化趋势,叶片转子和发电机转子的动态响应结果与风速的变化趋势大致相同，但幅值略有不同，柔性传动模型动态响应幅值低于刚性载荷传递模型。

(3)考虑主轴及高速轴柔性的实际影响,为得到更准确的计算结果,在研究中需更多地考虑传动系统柔性对系统振动及稳定性的影响。

(4)存在最佳主轴刚度值使得系统受到的冲击作用最小。

[1]林茂峰,孙文磊,胡斌.750kW风力发电机齿轮箱动力学分析[J].机械工程与自动化,2010,159(2):17-19.

Lin Maofeng.Sun Wenlei,Hu Bin.Dynamic Aualysis of 750kW Wind Turbine Gear Box[J].Mechanical Engineering & Automation,2010,159(2):17-19.

[2]邹磊，贾涛，宁新宇，等. 低风速风力发电机轮毂强度与疲劳寿命分析[J]. 可再生能源，2011，29(5): 28-31.

Zuo Lei,Jia Tao,Ning Xinyu,et al.Strength and Fatigue Analysis of Low Wind Speed Turbine Hub[J].Renewable Energy Resources,2011,29(5):28-31.

[3]陈严,欧阳高飞,伍海滨,等.变转速风力机的动态模型与随机载荷下的动态分析[J].太阳能学报,2004,25(6):723-727.

Chen Yan,Ouyang Gaofei,Wu Haibing,et al.Dynamic Model and Analysis for Variable Speed Wind Turbine[J].Acta Energiae Solaris Sinica,2004,25(6):723-727.

[4]陈严,杜明慧.变转速风力机全系统性能分析[J].汕头大学学报(自然科学版)，2005,20(3):41-47.

Chen Yan,Du Minghui.Research on the Entire Set Property of Variable Speed Wind Turbine[J].Journal of Shantou University(Nature Science),2005,20(3):41-47.

[5]秦大同,龙威,杨军,等.变风速运行控制下风电传动系统的动态特性[J].机械工程学报,2012,48(7):1-8.

Qin Datong,Long Wei,Yang Jun,et al.Dynamic Characteristics of Wind Turbine Transmission System under Verying Winds Speed and Operation Control Cenditions[J].Journal of Mechanical Engineering,2012,48(7):1-8.

[6]杨军,秦大同,陈会涛,等.风力发电机传动系统随机风速下的载荷特性研究[J]. 中国机械工程,2011,22(15):1837-1841.

Yang Jun,Qin Datong,Chen Huitao,et al.Research on Dynamic Load of Wind power Generation Tronsmission System under Random Wind[J].China Mechanical Engineering,2011,22(15):1837-1841.

Wang Liping,Zhou Min.Study on the Reasonable Determination of an Average Wind Velocity in the Gaussion Atmospheric Diffusion Model[J].Journal of China University of Mining & Technology,1995，24(2):89-93.

[8]A Iannuzzi,P Spinelli.Artificial Wind Generation and Structural Response[J].Journal of Structural Engineering,ASCE,1987,113(10):2382-2398.

[9]舒新玲，周岱. 风速时程AR模型及其快速实现[J]. 空间结构，2003,9(4):27-32.

Shu Xinling,Zhou Dai.AR Model of Wind Speed Time Series and Its Rapid Implementation[J].Spatial Structures,2003,9(4):27-32.

[10]Van der Hooft E L,Schaak P,Van Engelen T G.Wind Turbine Control Algorithms[R].Netherlands:Energy Research Centre of the Netherlands,2003.

[11]Shiau B S,Chen Y B.Observation on Wind Turbulence Characteristics and Velocity Spectra Near the Ground at the Coastal Region[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90(12):1671-1681.

[12]王守新.材料力学[M].大连:大连理工大学出版社,2005.

[13]Li Y, Kareen. ARMA Representation of Wind Field[J].Journal of Wind Engineering and Industrial Aerodynamics,1990,36(Part 1):415-427.

[14]Mario D P.Digital Simulation of Wind Field Velocity[J].Journal of Wind Engineering and Industrial Aerodynamics.1998,74-76:91-109.

[15]Bossayi E A.Bladed for Windows Theory Manual[M].England:Garrad Hassan and Partners Ltd,1999.

(编辑郭伟)

Research on Load Transmitting Characteristics Wind Turbine under Random Wind Speed

Wang YangSun WeiWei JingLi XiangHu Xinglong

Dalian University of Technology,Dalian,Liaoning,110624

Exponential function was used to describe the average wind speed,and the auto-regressive method was used to simulate nature random wind speed.Based on the moment of momentum theorem and simple spring-mass-damping model,the rigid drive model and flexible drive model of a wind turbine transmission system were established to describe the dynamic characteristics of the system.According to the parameters of 5 MW variable speed and variable pitch wind turbine,the influences of the two different drive trains on the dynamic response of rotor blade and generator rotor under the random wind speed were calculated and analyzed and the results of dynamic response were compared.Based on flexible transmission system model,the influences of different main shaft stiffnesses on the dynamic response of transmission system were discussed to obtain the optimum main shaft stiffness,and rainflow counting method was utilized to describe the dynamic response of transmission system under different main shaft stiffnesses.The results provide load data for the research of dynamic characteristics of transmission system of wind turbine.

auto-regressive model;transmission system;load transmittion;rainflow counting

2013-04-06

2004-07-28

国家国际科技合作项目(2011DFB71670);中央高校基本科研业务费专项资金资助项目(DUT12LAB11)

TK8DOI：10.3969/j.issn.1004-132X.2015.02.003

王洋,女,1989年生。大连理工大学机械工程学院硕士研究生。主要研究方向为大功率发电机增速器的设计与开发。孙伟，男,1967年生。大连理工大学机械工程学院教授、博士研究生导师。魏静,男，1978年生。大连理工大学机械工程学院副教授。