表面粗糙度对三维应力集中系数及疲劳寿命的影响

廖智奇　吴运新　袁海洋

中南大学高性能复杂制造国家重点实验室,长沙,410083

表面粗糙度对三维应力集中系数及疲劳寿命的影响

廖智奇吴运新袁海洋

中南大学高性能复杂制造国家重点实验室,长沙,410083

利用半椭圆微缺口表征表面粗糙度，建立了平板表面形貌的三维有限元模型，总结了微缺口参数对表面应力集中系数的影响规律。建立了表面应力集中系数与表面粗糙度之间的经验公式，预测了不同表面粗糙度下平板的疲劳寿命。研究结果表明：应力集中系数与表面粗糙度成正相关关系；当缺口数大于10时，应力集中系数随缺口数的增加而恒定；当间宽比大于5时，多缺口已经失去缓和应力集中的作用；疲劳寿命随着表面粗糙度的增加而缩短。

表面粗糙度；半椭圆微缺口；应力集中系数；疲劳寿命

0　引言

表面粗糙度是指由加工表面上的较小间距和峰谷所组成的微观几何形状特征,对疲劳寿命有非常显著的影响。试验表明，疲劳寿命随表面粗糙度的降低而延长[1-2]。疲劳性能是航空件可靠性及寿命的决定性因素，而表面加工质量的好坏将直接影响航空件的疲劳性能[3-4],所以研究表面粗糙度对疲劳寿命的影响很有意义。

刘军等[10]研究了孔壁粗糙度对疲劳寿命的影响,王启智等[11]研究了椭圆孔板的应力集中系数表达式,王元清等[12]将三维缺口应力集中系数用于求解应力强度因子。以上研究都利用椭圆孔来模拟表面微观形貌，研究了应力集中系数并将其应用到疲劳寿命的研究中。但在三维模型下，利用半椭圆微缺口模拟表面形貌，探讨表面粗糙度与应力集中系数的关系，并进一步推导其与疲劳寿命的关系还缺乏研究。本文目的是在三维层面下，建立表征表面粗糙度的表面半椭圆微缺口平板模型,利用有限元方法探寻表面粗糙度与表面应力集中系数Kt的经验公式,并用于预测疲劳寿命。

1　有限元模型

如图1所示,整体模型为一平板，在平板的一面上添加半椭圆微缺口，在两侧面上施加均布拉伸载荷p=100 MPa。椭圆半径a为微缺口半宽度，半径b为微缺口深度，d为缺口间距(图1中2个缺口中心线的间距)。机械加工后板材的表面粗糙度Rz约为1.6～12.5 μm,因而缺口参数在1～ 12 μm间取值。由于三维应力集中扩散速度较大,因此模型的最小尺寸要大于微缺口尺寸的2倍[13],平板尺寸为0.5 mm×0.2 mm×0.1 mm,在0.5 mm×0.1 mm的面上(以下称考察面)施加半椭圆微缺口来模拟平板表面形貌。本文基于7075T651铝合金材料进行研究,该材料具有高的强度和韧性,但加工时容易产生各种表面缺陷[4],其弹性模量E=71 GPa，泊松比μ=0.33[14]。

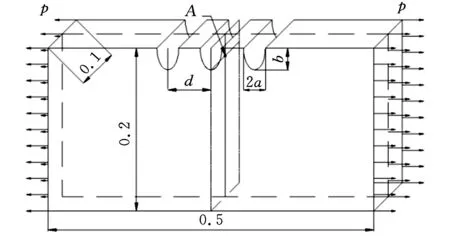
图1　模型示意图

为了消除边缘效应的影响,在此取模型中间微缺口底部线中点为考察点(图1中的A点)，取A点的Mises应力为最大应力σmax,由于缺口尺寸相对于模型尺寸较小，因此将p代替净截面名义应力σn代入公式计算Kt,即可准确地计算微缺口处的应力集中系数Kt[9]。

本文采用的应力集中系数定义如下：

Kt=σmax/σn

(1)

2　有限元结果及其分析

将建立好的模型提交计算分析后，可得应力云场,将A点的Mises应力代入式(1),即可求得不同微缺口参数下的应力集中系数。先研究单微缺口下微缺口参数对应力集中系数Kt的影响规律,再扩展为多微缺口模型。

2.1单微缺口下微缺口参数对应力集中系数的影响

在考察面中间位置施加微缺口,建立单微缺口的三维表面形貌模型，研究微缺口深度b与微缺口半宽度a的比值(以下简称深宽比b/a)及微缺口深度b对应力集中系数Kt的影响。

模型的深宽比b/a在2～10间取值5组,深度b在1～ 6 μm间取值6组,共计30个模型,分别提取Kt与b及b/a的关系,绘制出Kt与b的关系曲线(图2)和Kt与b/a的关系曲线(图3)。

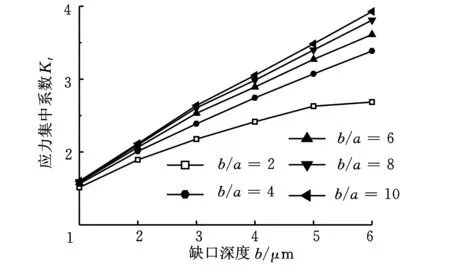
图2　单微缺口的Kt与b关系曲线

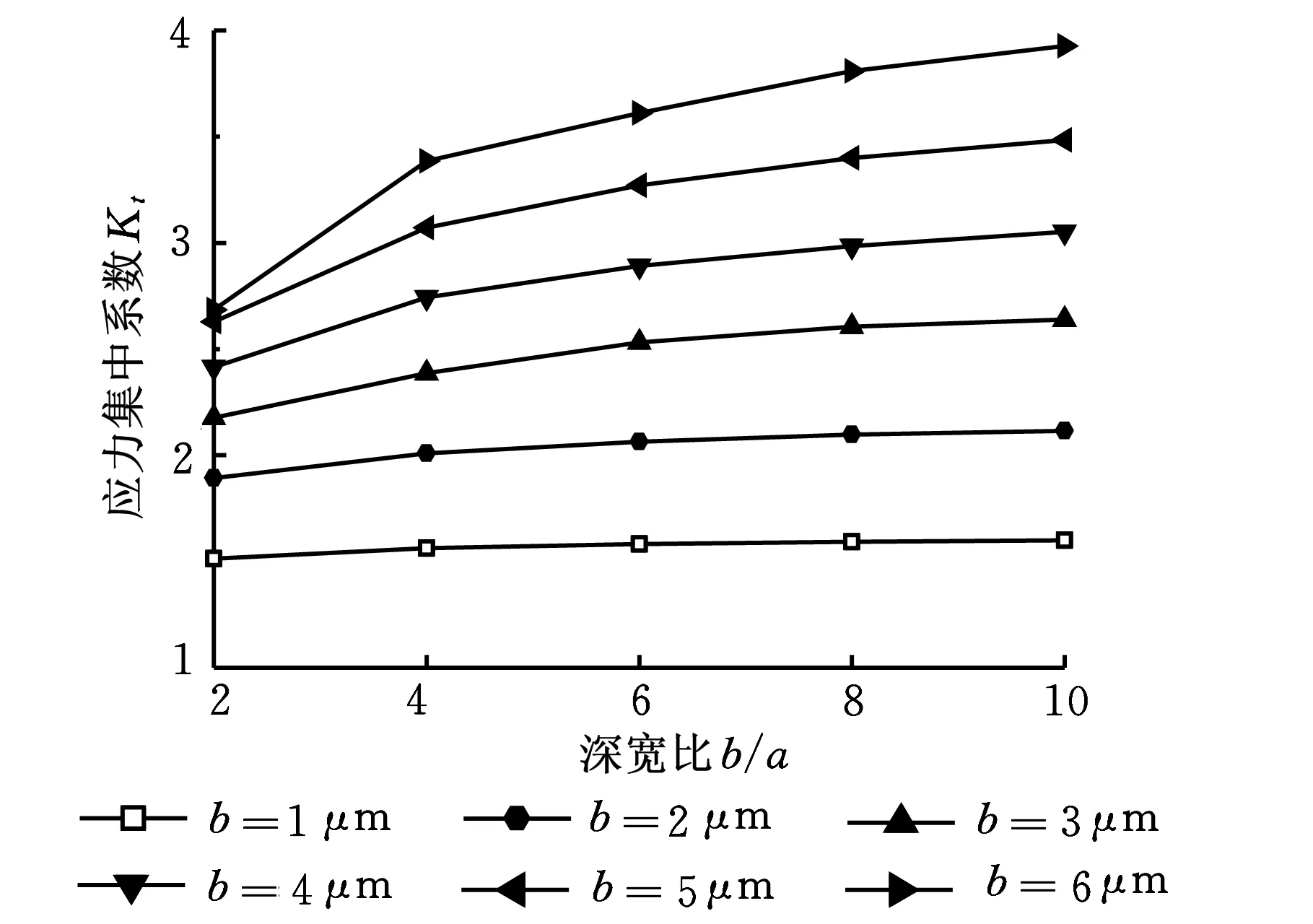
图3　单微缺口的Kt与b/a关系曲线

由图2可知,b增加时,Kt也随之增加;曲线都较为陡峭,表明Kt对b比较敏感。综合来看,b/a由2增加到10的过程中，曲线斜率增加但截距不变，且相邻曲线间距越来越小，这意味着b/a越大,b对Kt的影响越明显,但其增加幅度越小。

由图3可知,随着b/a的增加,Kt也增加;曲线都较为平缓,表明此时Kt对b/a并不很敏感。综合来看,b由1 μm增加到6 μm的过程中,曲线斜率变化不大,且相邻曲线间距基本不变,这表明b的变化对b/a及Kt的影响趋势改变很小。

2.2多微缺口下微缺口参数对应力集中系数的影响

在模型考察面上对称分布多个等间距微缺口，建立多微缺口下的三维表面形貌模型，研究微缺口间距d和缺口宽度2a的比值d/(2a)(以下简称间宽比)和微缺口深宽比b/a对应力集中系数Kt的影响。

2.2.1微缺口个数对应力集中系数的影响

首先探讨微缺口个数n对应力集中系数Kt的影响。取微缺口深度b=4 μm,深宽比b/a=2,缺口中心距d在4～12 μm间取值5组,在模型考察面上对称分布1～15个等间距缺口,共计40个模型,将模型进行计算得到多组Kt,绘制出Kt与n的关系曲线,如图4所示。

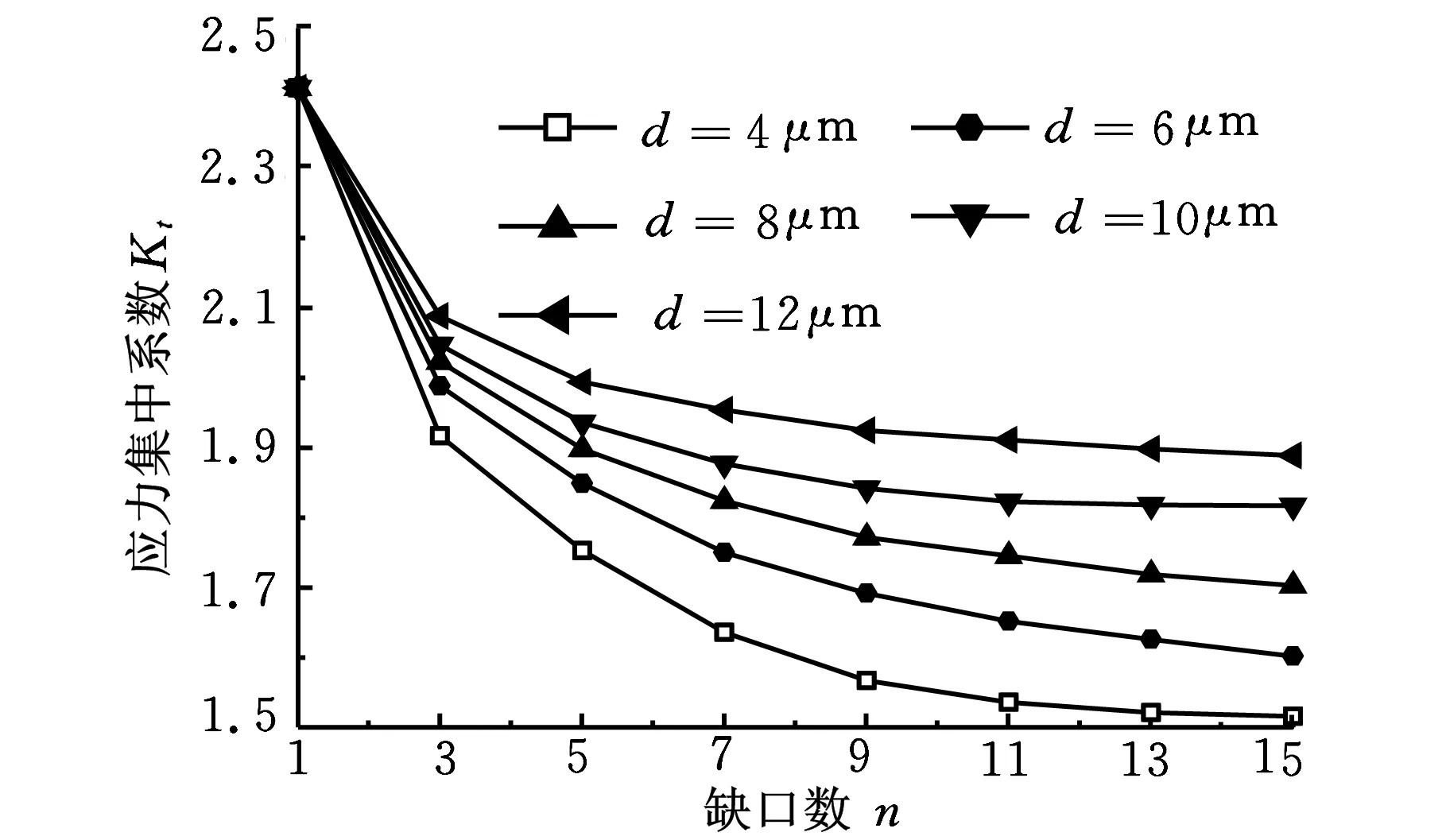
图4　多微缺口缺口数目n与Kt关系曲线

观察图4可知,在一定范围内,随着n的增加,Kt逐步减小;n≥10时,相邻缺口数目的Kt已相当接近了，表明此时n对Kt的影响就很小了，由此可以认为用n≥10计算出来的Kt等效于n=∞时的Kt。

2.2.2多微缺口参数对应力集中系数的影响

参考以上的结论,选取15个相同的等间距微缺口,其他条件与前面一致，分别计算微缺口深宽比b/a=2,3，…，6，间宽比d/(2a)=1，2，…，5的多微缺口应力集中系数Kt,共计25个模型，绘制出Kt与d/(2a)的关系曲线(图5)、Kt与b/a的关系曲线(图6)。

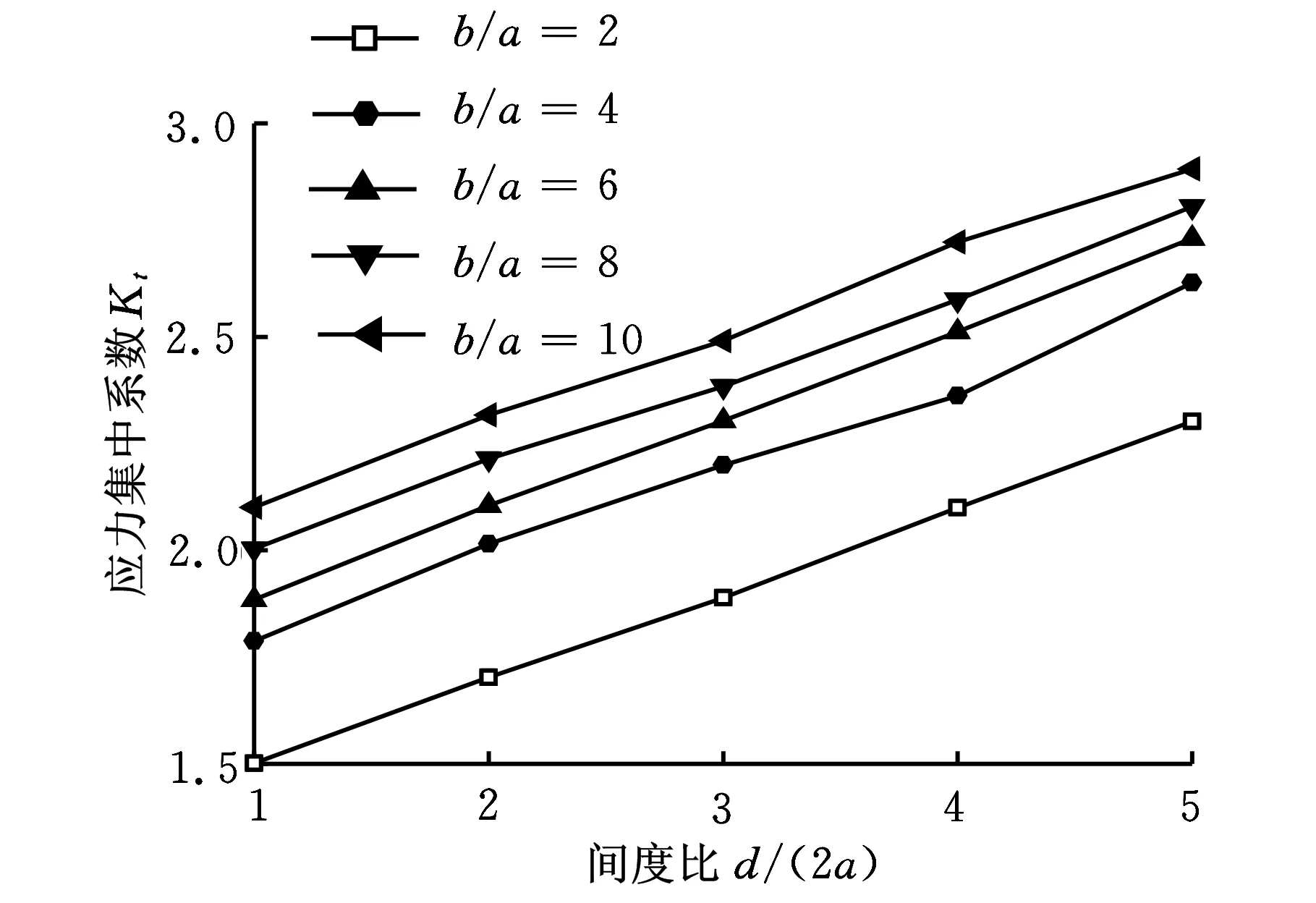
图5　多微缺口间宽比d/(2a)与Kt关系曲线

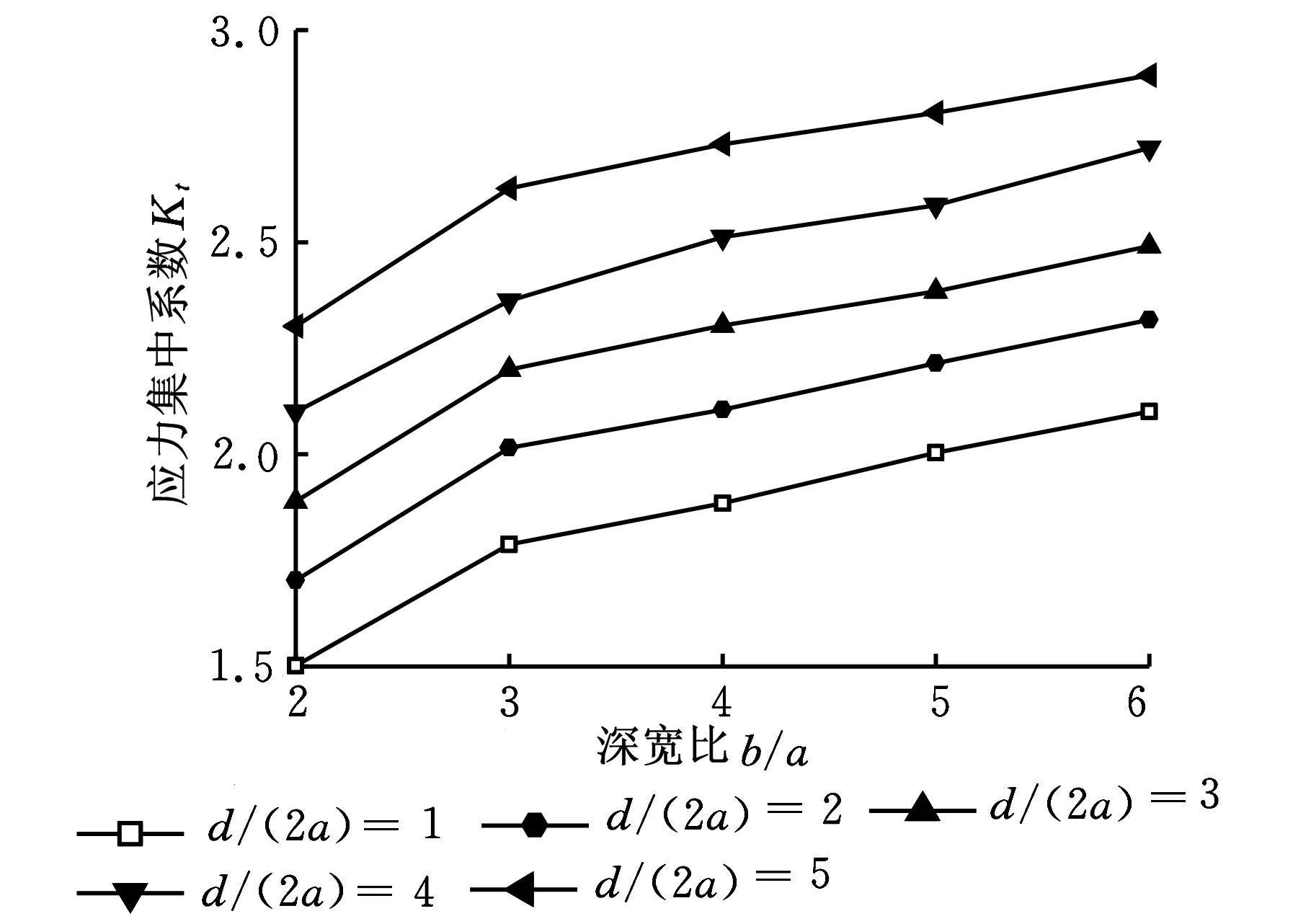
图6　多微缺口深宽比b/a与Kt关系曲线

由图5可知,Kt-d/(2a)的曲线是一条近似线性的曲线，随着d/(2a)的增加,Kt增大。综合来看,b/a由2增加到6的过程中，各曲线斜率近似相同，这表明d/(2a)对Kt的影响趋势几乎不受b/a变化的影响。由图6可知,b/a越大,Kt也越大；d/(2a)=5时，曲线与单微缺口曲线几乎重合，表明多微缺口Kt十分接近单微缺口Kt,这是因为间距过大，会使每个微缺口以各自独立的形式产生应力集中，从而失去缓和应力集中的作用[13]。

3　公式拟合

利用最小二乘拟合表1中数据，得到相关系数均为0.999，最大误差为4.14%的单微缺口Kt与b/a及b的经验公式：

Kt=0.36+1.08(a/b)0.5+1.21b0.72-1.07(a/b)0.5b0.72

(2)

观察图5可知，Kt与d/(2a)成线性关系，因此在拟合公式中先确定d/(2a)的指数(为1),利用最小二乘拟合相应数据，得到相关系数为0.998,最大误差为3.47%的多微缺口Kt与b/a及d/(2a)的经验公式：

Kt=2.7-2(a/b)0.5+0.1d/a

(3)

为了验证以上经验公式的正确性,任取若干组微缺口参数进行仿真，将仿真结果与拟合结果进行比较，如表1、表2所示。

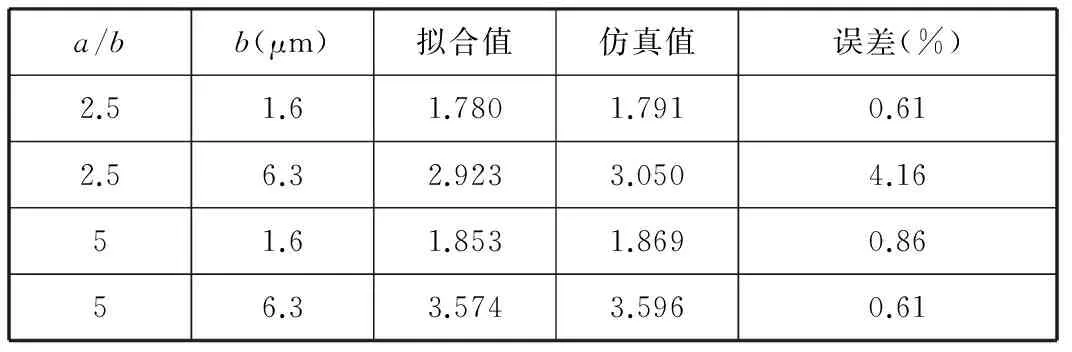
表1　单微缺口经验公式拟合误差

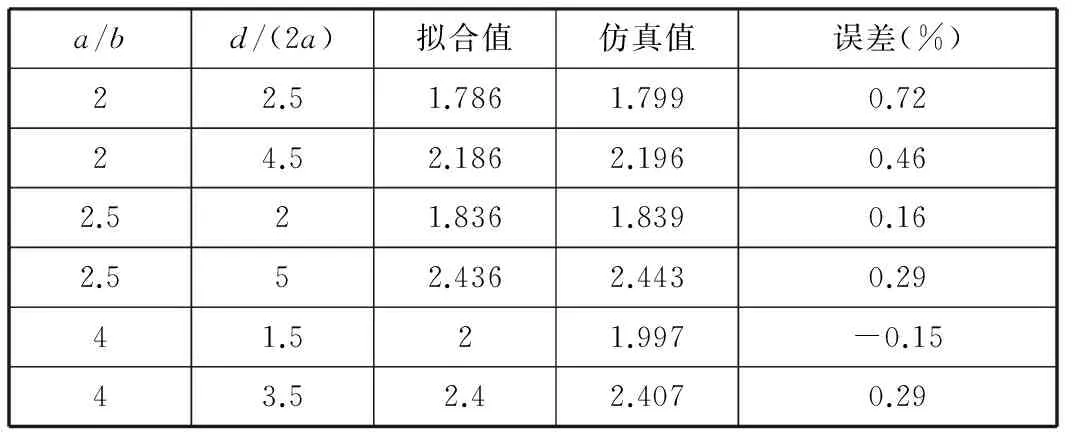
表2　多微缺口经验公式拟合误差

式(2)所得的拟合值与仿真值最大误差为4.16%,式(3) 所得的拟合值与仿真值最大误差为0.72%,以上两式的计算结果与仿真结果的误差均小于5%,证明这些经验公式是准确的。

4　缺口参数和表面粗糙度转换

缺口参数b与缺口间距d可以用表面粗糙度的十点不平度参数Rz和轮廓单峰平均间距S进行转换，以上参量如图7所示。

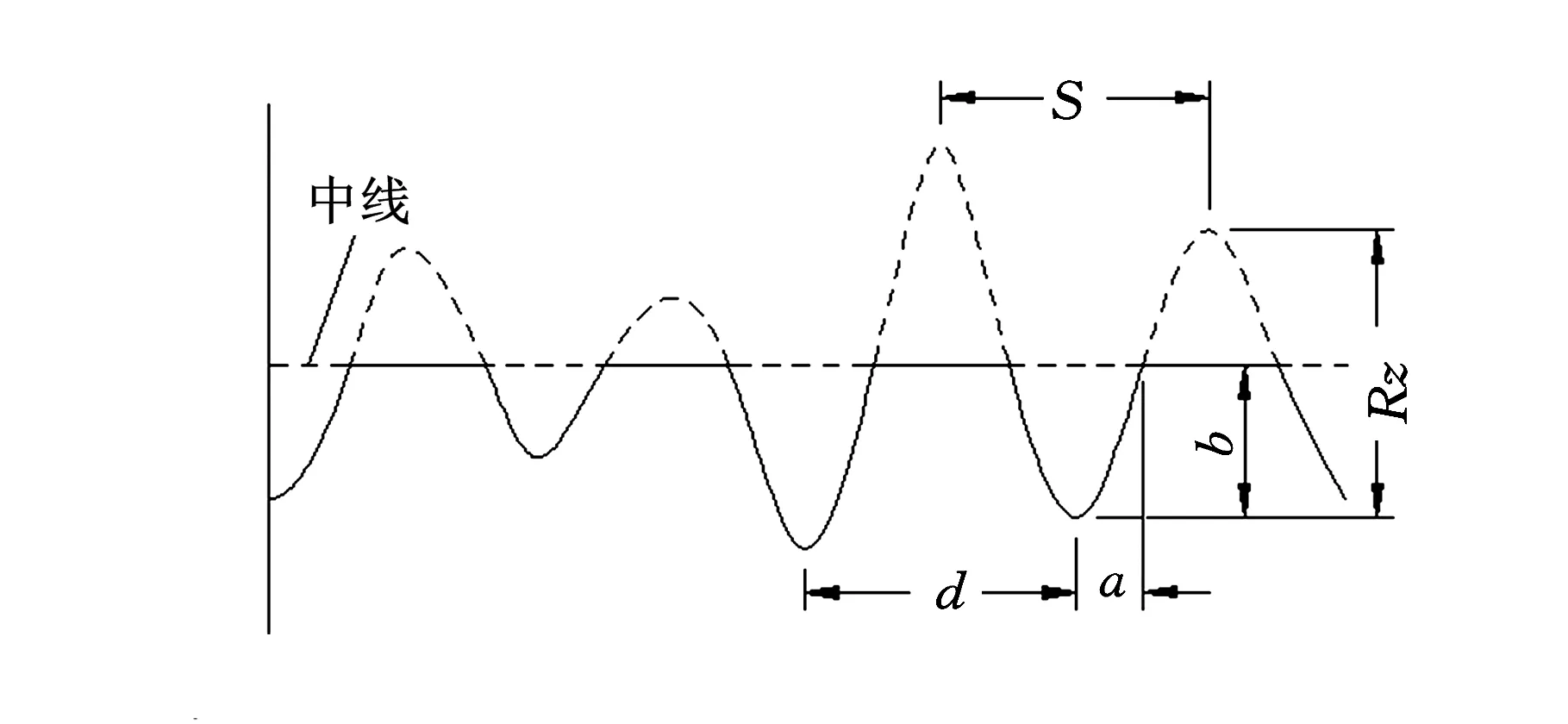
图7　表面粗糙度意图

图7为平板表面粗糙度示意图,由于粗糙度参数是采用一个取样长度内的平均值,因此可得b=Rz/2,d=S,假设一个参量A,且深宽比b/a=1/A,将以上等价关系代入式(3),得到表面粗糙度与表面应力集中系数的经验公式：

(4)

5　疲劳寿命预测

将加工后的7075铝板表面形貌简化为连续多微缺口模型，研究不同粗糙度Rz时平板的疲劳寿命。文献[15]给出了较完善的疲劳寿命表达式：

N=Sf/(Segv-Segv,c)2

(5)

其中,Sf为应力疲劳抗力系数;Segv,c为用当量名义应力幅表示的理论疲劳极限。7075铝合金的Sf=8.91×108MPa2,Segv,c=112 MPa。Segv为当量名义应力幅，其计算公式为

(6)

当应力比R=-1,Smax=σn=100 MPa时有

Segv=100Kt

(7)

若测得轮廓单峰平均间距S=6 μm,根据式(4)计算出不同表面十点不平度Rz下的应力集中系数Kt,结合式(5)、式(7),可以得到疲劳寿命N,绘制出对数疲劳寿命lgN与表面粗糙度Rz的关系曲线,如图8所示。

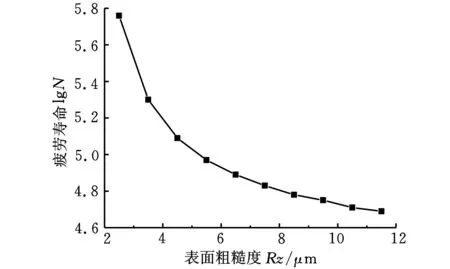
图8　粗糙度Rz与对数疲劳寿命lgN关系曲线

从图8可以看出,随着粗糙度Rz的增加,缺口的疲劳寿命不断减少。对表中数据进行拟合,得到表面粗糙度Rz与对数疲劳寿命lgN之间的经验公式：

lgN=4.496+2.112/Rz+2.621/(Rz)2

(8)

式(8)所得的拟合值与仿真值最大误差为-2.16%,相关系数在0.999以上,为了验证式(8)的准确性，取粗糙度Rz=3.2,4,6.3,8,12.5 μm,用式(8)计算得到疲劳寿命，并与式(4)、式(5)、式(7)联合计算结果进行对比，如表3所示。

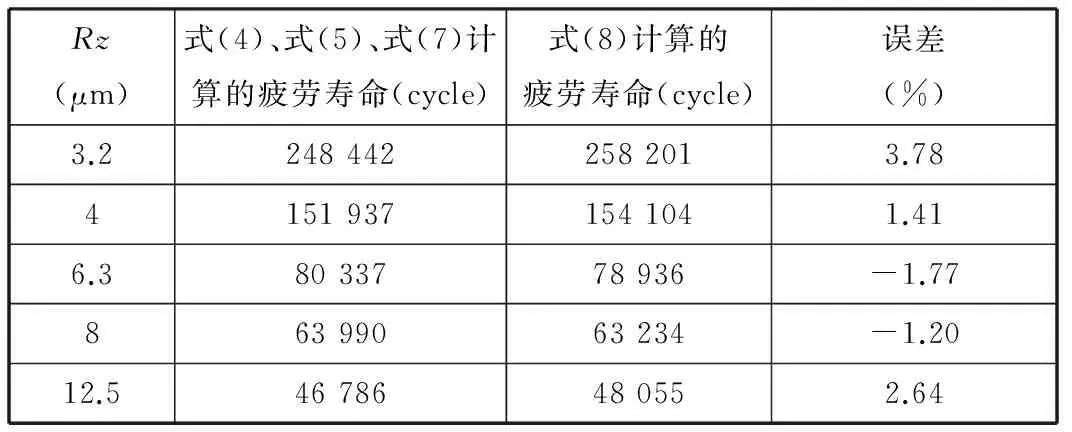
表3　两种方式计算得到的疲劳寿命对比

由表7可知,式(8)计算结果与式(4)、式(5)、式(7)计算结果的最大相对误差为3.78%,表明利用式(8)计算结果准确。

6　结论

(1)单微缺口应力集中系数Kt与表面粗糙度Rz及深宽比b/a均成正相关。b/a越大时,表面粗糙度Rz对Kt的影响越明显,但其增加幅度越小;表面粗糙度Rz变化时,b/a对Kt的影响趋势变化很小。

(2)在一定范围内,随着n的增加,Kt逐步减小,缺口数n≥10时,Kt随n的增加而恒定,表明此时n对Kt的影响很小了,由此可以认为用n≥10计算出来的Kt等效于n=∞时的Kt。

(3)多微缺口应力集中系数Kt与间宽比d/(2a)及深宽比b/a成正相关关系。b/a和d/(2a)分别变化时，另一因素对Kt的影响趋势几乎不变。d/(2a)=5时，多微缺口Kt已经十分接近单微缺口Kt，表明此时多微缺口已经失去缓和应力集中的作用。

(4)建立了表面粗糙度与应力集中系数Kt及疲劳寿命N间的经验公式，并验证其具有较好的准确性。研究表明，疲劳寿命N随着表面粗糙度Rz的增加而缩短。

[1]Zahavi E,Torbilo V,Press S.Fatigue Design:Life Expectancy of Machine Parts[M].London:CRC Press,1996.

[2]张东初,裴旭明.加工工艺对表面粗糙度及疲劳寿命的影响[J]. 中国机械工程，2003,14(16):1374-1377.

Zhang Dongchu,Pei Xuming.Effects of Machining Processes on Surface Roughness and Fatigue Life[J].China Mechanical Engineering,2003,14(16):1374-1377.

[3]曾泉人,刘更,刘岚.机械加工零件表面完整性表征模型研究[J].中国机械工程,2010,21(24):2995-2999.

Zeng Quanren,Liu Geng,Liu Lan.Quantitative Description Model of Surface Integrity for Machined Parts[J].China Mechanical Engineering,2010,21(24):2995-2999.

[4]裴旭明,陈五一,任炳义,等.加工工艺对7075铝合金紧固孔表面形貌和组织的影响[J].中国有色金属学报,2001,11(4)：655-660.

Pei Xuming,Chen Wuyi,Ren Bingyi,et al.Influence of Machining Processes on Surface Microphotograph and Microstructure of Fastening Holes[J].The Chinese Journal of Nonferrous Metals,2001,11(4): 655-660.

[5]岳珠峰.多晶体光滑表面疲劳微裂纹形核机理研究[J].应用数学和力学,2004,25(8)：809-814.

Yue Zhufeng.On the Study of the Initiation of the Micro Crack on the Smooth Surface of Polycrystalline[J].Applied Mathematics and Mechanics,2004,25(8):809-814.

[6]Arola D,Williams C L.Estimating the Fatigue Stress Concentration Factor of Machined Surfaces[J].International Journal of Fatigue,2002,24(9):923-930.[7]Andrews S,Sehitoglu H.A Computer Model for Fatigue Crack Growth from Rough Surfaces[J].International Journal of Fatigue,2000,22(7)：619-630.

[9]章刚，刘军，刘永寿，等. 表面粗糙度对表面应力集中系数和疲劳寿命影响分析[J]. 机械强度，2010(1)：110-115.

Zhang Gang,Liu Jun,Liu Yongshou,et al.Effect of Roughness on Surface Stress Concentration Factor and Fatigue Life[J].Journal of Mechanical Strength,2010(1):110-115.

[10]刘军,刘勇俊,刘永寿,等.开孔试件的表面粗糙度对疲劳寿命影响的定量分析[J].中国机械工程,2008,19(3):327-329.

Liu Jun,Liu Yongjun,Liu Yongshou,et al.Quantitative Analysis of Roughness Effect on Fatigue Life of Specimen with Open Holes[J].China Mechanical Engineering,2008,19(3):327-329.

[11]王启智,戴峰.拉伸半无限圆孔板应力集中系数研究[J].四川大学学报(工程科学版),2002,34(4):5-9.

Wang Qizhi,Dai Feng.A Study of Stress Concentration Factors for Tension Semi-infinite Plate with a Circular Hole[J].Journal of Sichuan University(Engineering Science Edition),2002,34(4):5-9.

[12]王元清,武延民,王晓哲,等.含缺口受拉平板三维应力场及其对脆性破坏的影响[J].清华大学学报(自然科学版),2002,42(6):832-834.

Wang Yuanqing,Wu Yanmin,Wang Xiaozhe,et al.3-D Stresses in a Flat Slab with a Crack in Tension and the Effect on Brittle Fracture[J].Journal of Tsinghua University (Sci & Tech),2002,42(6)：832-834.

[13]西田正孝.应力集中[M].李安定,译.北京:机械工业出版社,1986.

[14]黄伯云，邱冠周. 有色金属材料手册[M]. 北京：化学工业出版社，2009.

[15]郑修麟. 金属疲劳的定量理论[M]. 西安：西北工业大学出版社，1994.

(编辑张洋)

Influences of Surface Roughness on Three Dimensional Stress Concentration Factor and Fatigue Life

Liao ZhiqiWu YunxinYuan Haiyang

State Key Laboratory for High Performance Complex Manufacturing,Central South University,Changsha,410083

According to building three dimensional finite element model of plate surface topography,whose surface roughness were represented as the semi-ellipse micro-notches,the influences of micro-notch parameters on surface stress concentration factors were summed up.Empirical equation that related surface roughness to surface stress concentration factors of plate was established and predicted the fatigue life of the plate under different surface roughnesses.Research results show that:it is positive between stress concentration factor and surface roughness;when the number of notch is over 10,stress concentration factor is constant with the increase of the number of notch;when the ratio is over 5,multi-notches have been out of action to lessen the stress concentration;when surface roughness increases,the fatigue life decreases.

surface roughness;semi-ellipse micro-notch;stress concentration factor;fatigue life

2013-06-09

国家重点基础研究发展计划(973计划)资助项目(2010CB731703)

V252.2;O346.23< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.02.002

廖智奇,男,1988年生。中南大学机电工程学院硕士研究生。主要研究方向为高性能铝材疲劳裂纹及构件损伤容限。吴运新,男,1963年生。中南大学机电工程学院教授、博士研究生导师。袁海洋,男,1982年生。中南大学机电工程学院博士研究生。