浮动平底推杆凸轮机构的第Ⅱ类尺寸综合问题
李延平 林荣富 常 勇
集美大学,厦门,361021
浮动平底推杆凸轮机构的第Ⅱ类尺寸综合问题
李延平林荣富常勇
集美大学,厦门,361021
将德国进口高速印刷机机构中的滚子推杆推广至平底推杆演化构型,并以此为研究对象,引入“斜交浮动坐标系”、“支撑函数法”和“瞬时一维直线区段”及其投影得到的“瞬时区间套”等概念,进而提出求解推程区间套、回程区间套和整程区间套的方法。给出求解瞬时/整程平底方位线许用选择区域和凸轮基圆半径r0许用取值范围的基本原理,并推导得到其相应的通用解析公式,进而得到其解的存在性和存在性态的解析判据,最后搜索得到平底夹角的取值范围等。较圆满地解决了浮动平底推杆盘形凸轮机构的第Ⅱ类尺寸综合问题。
浮动平底推杆;斜交浮动系;支撑函数;瞬时一维直线区段;瞬时/整程区间套;存在性态
0 引言
做平面运动的盘形凸轮机构按从动件类型可分为尖底从动件盘形凸轮、滚子从动件盘形凸轮和平底从动件盘形凸轮等。做平面运动的滚子从动件盘形凸轮机构[1-4]结构复杂,设计参数多且相互耦合,故其分析综合理论和方法更为复杂和繁琐。此机构不仅具有凸轮结构紧凑[5]的一般特点且易满足工程中对运动规律、运动轨迹和刚体导引等输出特性的要求。国内外已有许多学者[6-14]以压力角为评价指标对平面盘形凸轮机构进行了尺寸综合,对做平面运动的滚子从动件凸轮机构[15-18]的综合问题也作了相应研究。
与滚子从动件相比,平底从动件在承载能力、润滑性能、寿命和高速性能等方面具有显著优越性,常被应用于高速印刷机场合,故对平底从动件凸轮机构的研究具有理论探索和工程实用价值。
本文基于文献[1-2]将德国进口高速印刷机机构中的滚子推杆推广至平底推杆演化构型,并以此为研究对象,引入了“斜交浮动坐标系”、“支撑函数法”和“瞬时一维直线区段”及其投影得到的“瞬时区间套”等概念,进而提出“推程、回程和整程区间套”的概念,给出求解平底方位线许用选择区域、凸轮基圆半径r0许用取值范围的基本原理,据此推导得到求解计算的整套通用解析公式,进而得到解存在性和存在性态的系列解析判据,较圆满地解决了浮动平底推杆件盘形凸轮机构的第Ⅱ类机构综合问题。
1 浮动平底推杆演化机构第Ⅱ类尺寸综合问题的准确表述
图1所示为德国进口高速印刷机机构的浮动平底推杆演化机构。它由凸轮1、带平底的连杆2、摇块3、摇杆4和机架0组成,凸轮1、摇杆4分别为输入件和输出件。机构综合问题的准确描述如下。

(a)凸轮顺时针转动

(b)凸轮逆时针转动0.机架 1.凸轮 2.带平底的连杆 3.摇块 4.摇杆图1 浮动平底推杆凸轮机构

求解:满足α≤[α]∪ρ>0条件的平底线许用选择区域、凸轮基圆半径r0许用取值范围、平底工作段理论与实际长度。
2 若干基础性准备工作
2.1固定坐标系建立和预备公式推导
建立固定坐标系O1xy如图1所示。选凸轮轴心与O1重合,x轴方向与O1A一致,θ2、θ4分别为O1O2、AO2与x轴正向夹角,并令θ1为凸轮转角。
建立机构封闭矢量方程,并由图1中的几何关系得到连杆2即O1O2的长度、位置角和类角速度如下:
(1)
θ2=arctan(l4sin(θ40-β)/(l0+l4cos(θ40-β)))
(2)
dθ2/dθ1=-l4(dβ/dθ1)(l4+l0cos(θ40-β))/
(3)
连杆的绝对瞬心P20的坐标为
xP20=l0tan(θ40-β)/(tan(θ40-β)+cotθ2)
(4)
yP20=-l0tan(θ40-β)cotθ2/(tan(θ40-β)+cotθ2)
(5)
连杆的相对瞬心P21的坐标为
xP21=±[|dθ2/dθ1|/(±|dθ2/dθ1|-1)]·
[l0tan(θ40-β)/(tan(θ40-β)+cotθ2)]
(6)
yP21=±[|dθ2/dθ1|/(±|dθ2/dθ1|-1)]·
[-l0tan(θ40-β)cotθ2/(tan(θ40-β)+cotθ2)]
(7)
其中,“±”中的“+”表示同摆式机构,“-”表示异摆式机构[1]。
如图2所示,P21、P20间和P21、P10(P10为凸轮的绝对瞬心)间距离为
lP21P20=[(xP20-xP21)2+(yP20-yP21)2)]1/2
(8)
(9)
其中,lP21P20、lP21P10皆是θ1的一元函数,将lP21P20、lP21P10简记为l10和l21。

图2 浮动滚子/平底推杆机构满足α≤[α]条件解集的求解原理和内在联系
2.2“浮动坐标系”的设定
“浮动坐标系”[2]指固连于连杆平面Σ2上,以O2为原点,O2→u(O2u∥GG′)、O2→v(沿O2O1)为u轴、v轴正向的坐标系O2uv。简约起见,规定浮动坐标系的u、v两轴是斜交的——非正交的。
给定夹角σ,平底线GG′用其在O2uv中v坐标即可完全“锁定”。
如图1所示,夹角σ起始基准是O2′O1,且顺时针方向为正,理论取值范围为
0°<σ<180°
(10)
2.3推程前半/后半区段划分
连杆的绝对瞬心P20和相对瞬心P21又可细分为前后半区段的绝对和相对瞬心P20f、P20r和P21f、P21r,如图2所示。同样,连杆2与摇杆4的铰接点O2在前后半区段时分别表示为O2f和O2r。
整个推程,机构时为同摆式机构,时为异摆式机构(图3)[5],故根据其时变性,作如下划分:
前半区段:摇杆4位于O20A到O2bA之间,P20f位于O1O2的上方。
后半区段:摇杆4位于O2bA到O2mA之间,P20r位于O1O2的下方。
分界点O2b满足O2bA⊥O1O2b。此时P20位于垂直于O1O2的无穷远处。故有
cos(180°-θ40+β*)=l4/l0
(11)
β*=arccos(l4/l0)+θ40-180°
(12)


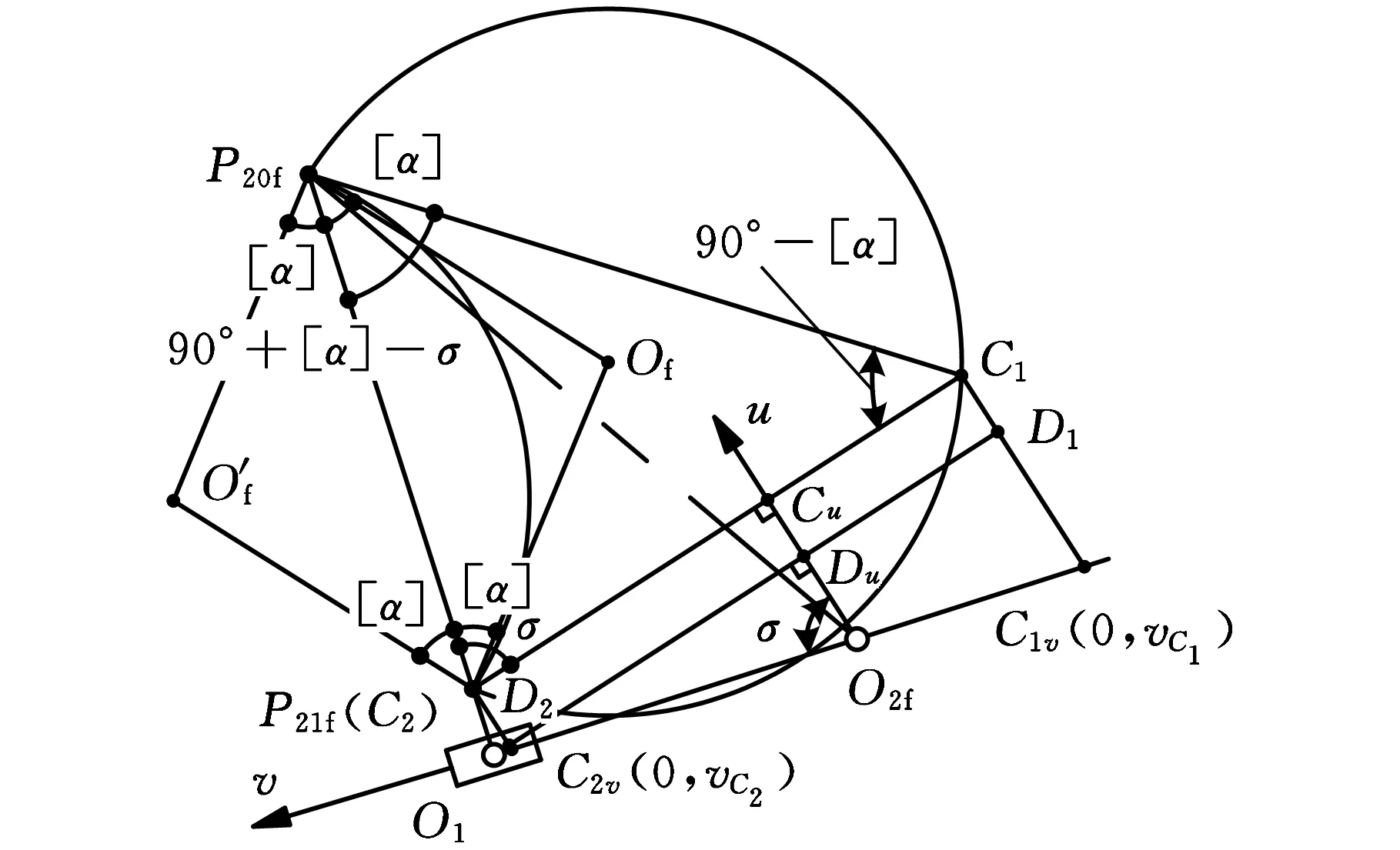
(a)前半区段
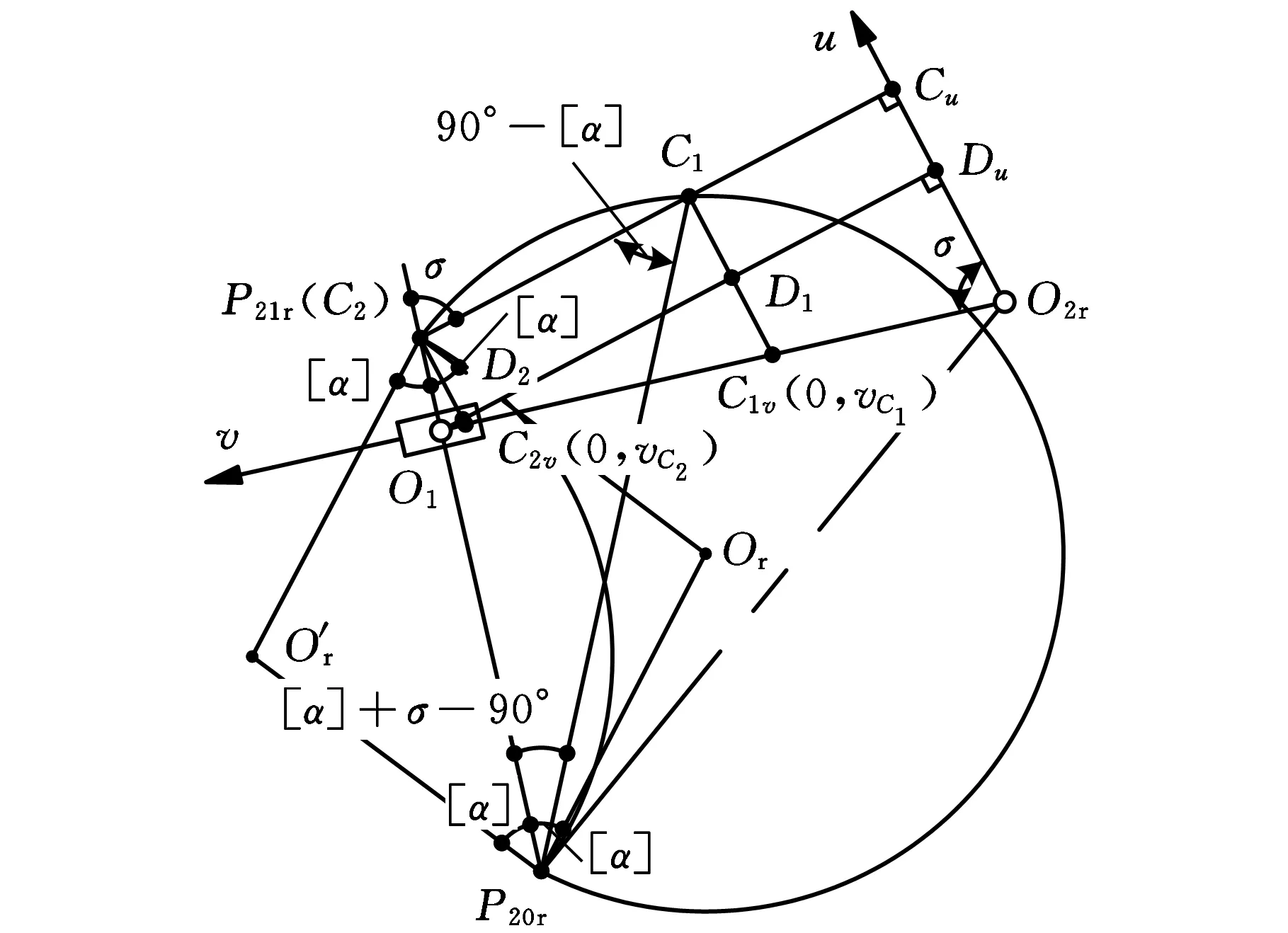
(b)后半区段,Ф0]图3 “瞬时一维直线区段”的u、v坐标推导
2.4“支撑函数法”的若干知识
2.4.1凸集的支撑线、支撑函数和方向角

图4 支撑函数与方向角
N为有界闭凸集,边界∂N为闭凸曲线,如图4所示。任选坐标系O1x′y′,自原点O1引射线O1R,O1R与x′轴正向夹角为φ(逆时针为正),作垂直于O1R且与N相交的任一直线G1(p1,φ),集合p1的上确界记为p,即
p=sup{p1:G1(p1,φ)∩N≠∅}
(13)
定义1与式(13)中p相对应的直线G(p,φ)称作凸集N沿φ方向的支撑线[19-21]。
定义2与式(13)中p相对应的函数p(φ)称作凸集N沿φ方向的支撑线。
定义3与式(13)中p相对应的角度φ称作支撑线G(p,φ)的方向角。
2.4.2凸集的充要条件
在∂N适当定向下,凸集成立的充要条件是曲率半径ρ恒为正,即

(14)
0≤φ<2π
3 满足α≤[α]条件机构解的存在性与存在性态
3.1凸轮顺时针转动
3.1.1推程
如图2所示,整个推程,P21始终位于连杆方位线O1O2上方。
机构任一瞬时位置,在连杆平面Σ2上,以P20P21为弦、朝O2v轴负向作优弧Cma、劣弧Cmi,使其满足:
∠P20CmajorP21=90°-[α]
(15)
∠P20CminorP21=90°+[α]
(16)
根据文献[2],该瞬时滚子推杆机构满足α≤[α]条件的K的全集为:由Cma、Cmi合作围成的“盈月形”二维平面区域Γ(u,v)。
如图3所示,再过P21(C2)引C2C1⊥u轴,分别交u轴、优弧Cma于Cu、C1点,则
C1C2∈Γ(u,v)
过C1、C2点,引C1C1v∥u轴、C2C2v∥u轴,分别交v轴于C1v和C2v点。再过O1点引u轴垂线,分别交C1C1v、u轴和C2C2v于D1、Du和D2点。于是,得到如下结论:平底推杆机构在某一瞬时位置满足α≤[α]条件的K的全集为:由C1C2构成的“瞬时一维直线区段”。
C1C2有如下特征:①是Γ(u,v)的真子集;②C2点对应的压力角αC2=0,C1点对应的压力角αC1=[α],且自C2到C1,α值由零单调增大至[α]。
据前述图解原理并据0°<σ<180°,易得到两点重要结论:
(1)若
90°-[α]<σ<90°+[α]
(17)
则任一瞬时皆存在C1C2,即机构有解。
(2)若
0°<σ≤90°-[α]或90°+[α]≤σ<180°
(18)
则任一瞬时皆不存在C1C2,即机构无解。
所以,下文均是在满足式(17)即机构有解的条件下进行讨论的。
C1C2在“浮动系”O2uv中的坐标为
uK=uC1(θ1)=uC2(θ1)=uK(θ1)
(19)
vK=vK(θ1)∈[vC1,vC2]=[vC1(θ1),vC2(θ1)]
(20)
其中,uK、vK皆是θ1的一元函数。
(1)推程前半区段。据图3a中几何关系,有
uK=uK(θ1)=O2Cu=O2Du+DuCu=
O2O1cosσ+D2C2=O2O1cosσ+O1C2sinσ=
s2(θ1)cosσ+η l21(θ1)sinσ
(21)
式中,η为行程系数,推程时η=1,回程时η=-1。
在△C1C2P20中,据正弦定理,有
P20C2/sin∠P20C1C2=C1C2/sin∠C1P20C2
(22)
又因为
∠P20C1C2=90°-[α]
(23)
∠P20C2C1=σ
(24)
∠C1P20C2=90°+[α]-σ
(25)
所以得
C1C2=P20C2sin(90°+[α]-σ)/sin(90°-[α])=
l10(θ1)cos(σ-[α])sec[α]
(26)
据上,可得
(27)
s2(θ1)-l21(θ1)cotσ-l10(θ1)cos(σ-[α])sec[α]cscσ
(28)
据式(21)、式(27)和式(28)知,uK、vC1和vC2皆是θ1的一元函数。
(2)推程后半区段。据图3b中几何关系、式(21),以及以下关系式:
∠P20C1C2=90°-[α]
(29)
∠P20C2C1=180°-σ
(30)
∠C1P20C2=[α]+σ-90°
(31)
得
C1C2=P20C2sin([α]+σ-90°)/sin(90°-[α])=
-l10(θ1)cos(σ+[α])sec[α]
(32)
可推演得到,式(21)和(27)为通用公式。而vC1则随式(29)~式(31)变为
vC1=vC2-C1vC2v=vC2-C1C2cscσ=
s2(θ1)-l21(θ1)cotσ+l10(θ1)cos(σ+[α])sec[α]cscσ
(33)
据式(21)、式(27)和式(33),uK、vC1和vC2仍是θ1的一元函数。
综上,即是将瞬时一维直线区段C1C2向u、v轴投影,u轴上得唯一点Cu,v轴上得C1v、C2v构成的“瞬时区间套”[vC1,vC2]。
于是,可得如下结论:①vK取在[vC1,vC2]两端点,即vK=vC1和vK=vC2时α=[α];②vK取在[vC1,vC2]内部,即vC1
证明从略。
选取uK、vK和θ1为纵横坐标,绘制vC1-θ1、vC2-θ1和uK-θ1曲线,如图5所示。

(a)不存在机构解

(b)存在唯一机构解
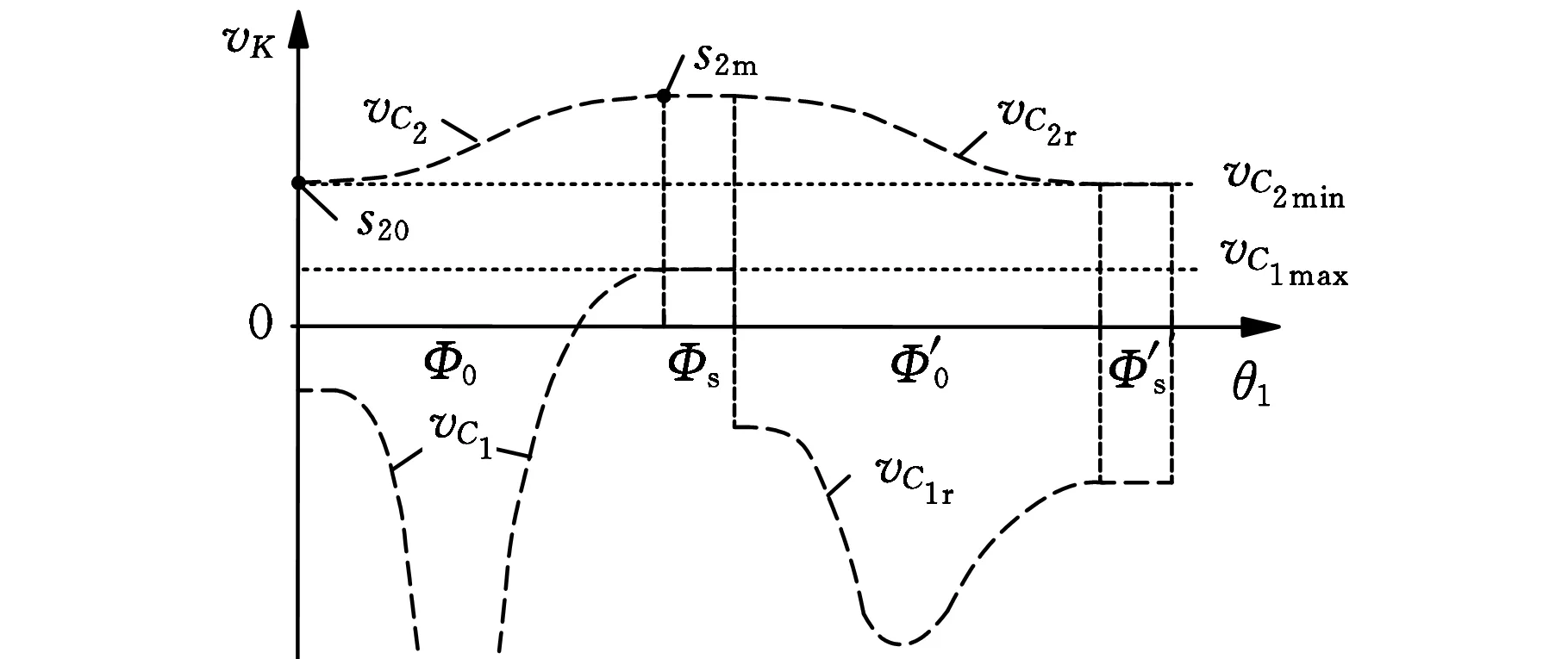
(c)存在无数机构解
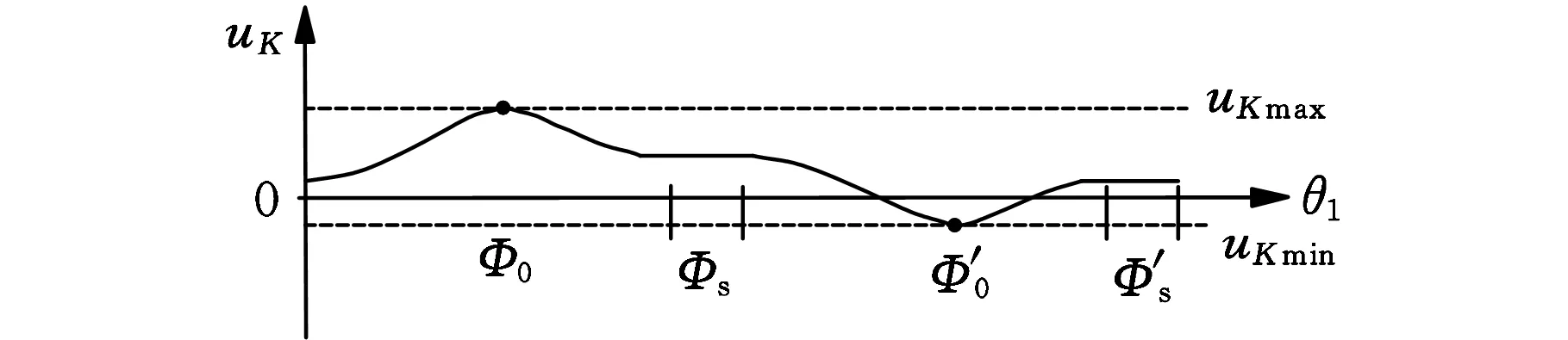
(d)uK-θ1曲线图5 vC1-θ1、vC2-θ1和uK-θ1曲线
整个推程,存在无数个“瞬时区间套” [vC1,vC2]。由此,解得“整程区间套”为
v∈[vC1max,vC2min]
(34)
据式(27)、式(28)、式(33),通过一维搜索解得推程vC2min、vC1max。
综上,可得如下重要结论:
(1)若
vC1max>vC2min
(35)
则
v∈[vC1max,vC2min]=∅
(36)
即满足α≤[α]条件的机构解不存在,如图5a所示。
(2)若
vC1max=vC2min
(37)
则
v∈[vC1max,vC2min]=Λ(独集)
(38)
即存在满足α≤[α]条件的唯一机构解为
v=vC1max=vC2min
(39)
如图5b所示。
(3)若
vC1max (40) 则 v∈[vC1max,vC2min]=Π(无穷集) (41) 即存在满足α≤[α]条件的无数机构解为 v∈[vC1max,vC2min] (42) 如图5c所示。 3.1.2回程 回程时[α]为70°~80°,推程的“整程区间套”一般嵌套在回程的“整程区间套”中,如图5虚线所示,故回程一般不予考虑。 3.2凸轮逆时针转动 研究方法与3.1节同理,这里从略。 拟采用“支撑函数法”[5-6]解决凸轮轮廓全部外凸,即“机构运动保真”问题。 4.1凸轮顺时针转动 4.1.1推程 图6 凸轮顺时针转动时支撑函数、方向角分析提取 (43) 方向角为 φ=θ1+(θ2-θ20) (44) 经系列推演,得凸轮轮廓曲率半径为 (45) (46) B=l4[l4+l0cos(θ40-β)] (47) Q=A3Bcos(θ40-β)-A3l0l4sin2(θ40-β)+ ABl0l4sin2(θ40-β) (48) E=A3[A2cos(θ40-β)+l0l4sin2(θ40-β)] (49) F=A5sin(θ40-β) (50) 据上知,ρ=ρ(θ1)是θ1的一元函数。一维搜索出使 (51) 成立的vρmax,则“推程区间套” v∈(-∞,vρ max)0≤θ1≤Ф0 (52) 即是满足推程凸轮轮廓外凸的解集。 4.1.2回程 同理,解得“回程区间套” v∈(-∞,vρ rmax) (53) 即是满足回程凸轮轮廓外凸的解集。 因为 r0=(s20-v)sinσ>0 (54) 故 v (55) 即有 (56) 4.1.3整程 根据4.1.1节和4.1.2节的求解结果,通过比较得出 (vρ)max=min(vρ max,vρ rmax) (57) 于是,得到的“整程区间套” v∈(-∞,(vρ)max)0≤θ1≤2π (58) 就是满足整程凸轮轮廓全部外凸即“机构运动保真”的解集。 基于式(56)和式(57),有 vρ max (59) 4.2凸轮逆时针转动 与4.1节同理,从略。 5.1凸轮顺时针转动 5.1.1平底线许用范围[vC1max,(vρ)max)与凸轮基圆半径r0许用取值范围的确定 综合第3和第4章,得重要结论: (1)若式(35)或式(37)成立,据式(59)知,满足α≤[α]∪ρ>0的机构解不存在。 (2)若式(40)成立,且 vC1max≥(vρ)max (60) 则满足α≤[α]∪ρ>0的机构解不存在。 若 vC1max<(vρ)max (61) 则存在满足α≤[α]∪ρ>0的无数机构解: v∈[vC1max,(vρ)max) (62) 此时 r0∈(r0min,r0max] (63) r0min=[s20-(vρ)max]sinσ (64) r0max=[s20-vC1max]sinσ (65) 如图7所示。 图7 存在无数机构解的情形 于是,得到如下重要结论:满足vC1max<(vρ)max,v值越大越靠近(vρ)max,r0和α越小,凸轮尺寸和传动性能越优。 5.1.2平底工作段及理论/实际长度的确定 (66) 据式(21),一维搜索解得推程uKmin、uKmax值和回程uKrmin、uKrmax值。比较筛选之,得到整程的(uK)min、(uK)max值: (uK)min=min(uKmin,uKrmin) (67) (uK)max=max(uKmax,uKrmax) (68) 再据式(66),有 (69) (70) 于是对于平底工作段,凸轮与平底接触点的集合为 (71) 平底理论长度为 (72) 平底实际长度为 L=l+(5~7)mm (73) 5.2凸轮逆时针转动 与5.1节同理,这里从略。 6.1凸轮顺时针转动 本节拟在满足α≤[α]∪ρ>0条件下,求解存在机构解的σ的取值范围。首先σ应满足式(17),即90°-[α]<σ<90°+[α]。 据第5章知:一个σ值对应GG′的一个许用取值范围[vC1max,(vρ)max)、r0的一个许用取值范围(r0min,r0max]和平底理论长度l,无数σ值对应无数机构解。故式(17)范围内,对σ作遍历性搜索,并以σ为横坐标,分别以平底线的v、凸轮基圆半径r0和平底理论长度l为纵坐标,可得v-σ、r0-σ和l-σ曲线,如图9所示。 图9 v-σ、r0-σ和l-σ曲线 于是,得到如下重要结论: (1)存在一个取值范围σ∈[σmin,σmax],即在该范围内,存在机构解。 (2)v-σ曲线包含vC-σ和vρ-σ两条曲线,vC-σ曲线据式(28)、式(33)和式(34)得到;vρ-σ水平直线据式(57)得到。其中vC-σ为单谷曲线,vρ-σ为水平直线。 (4)l-σ曲线为单峰曲线,l仅与σ有关,而与v无关。σ=σmax时,取得l的最小值lmin。给定σ值,l即为定值,但接触点的位置分布与v值有关。 需要强调的是:lmin是l的理论最小值(将v、σ皆视为变量的最小值),即全局最小值。 若视第2~5章研究的是浮动平底推杆机构的狭义第Ⅱ类综合问题[1],则本节讨论的就是其广义第Ⅱ类综合问题[2]。 6.2凸轮逆时针转动 与6.1节同理,这里从略。 (1)当σ为75°和85°时,①满足α≤[α]∪ρ>0条件的机构解;②凸轮最小基圆半径r0min;③平底工作段及理论/实际长度l和L。 下面是求解过程。 (1)将l0=140mm、l4=50mm、θ40=140°和β=0代入式(1),得s20=106.6554mm。 当σ=75°时,①据第3章理论公式,即α≤[α]条件解得v∈[vC1max,vC2min]=[72.1466mm,104.8224mm]。据第4章理论公式,即ρ>0条件解得v∈(-∞,(vρ)max]=(-∞,61.4900mm]。据第5章,因vC1max=72.1466mm>(vρ)max=61.4900mm,属式(40)、式(60)同时成立的情形,即此时不存在机构解。②其机构解不存在,故r0min的解也不存在。③其机构解不存在,故l和L的解也不存在。 本文通过引入“斜交浮动系”、“瞬时一维直线区段”等新概念,将文献[2]提出的浮动滚子推杆机构的求解原理推广和延拓至平底推杆机构的情况,并搜索得到平底夹角的有解取值范围,较为圆满地解决了浮动平底推杆盘形凸轮机构第Ⅱ类机构综合问题。值得指出的是,本文的对象机构虽源于印刷业的高速印刷机机构,但笔者已将其抽取提升成为共性机构学问题加以研究,所以本文的研究内容对许多行业装备的机构选型、分析与综合,具有参考价值。 [1]常勇, 杨富富. 作平面运动滚子从动件盘形凸轮机构的第Ⅱ类机构综合问题[J]. 机械工程学报, 2010, 46(21): 37-41. Chang Yong,Yang Fufu. Second Mechanism Synthesis Task of Disc Cam Mechanisms with Roller Follower Moving in Planar General Motion[J]. Journal of Mechanical Engineering,2010, 46(21):35-41. [2]常勇, 杨富富,胡志超,等. 作平面运动滚子从动件盘形凸轮机构的广义第Ⅱ类机构综合问题[J]. 机械工程学报, 2012, 48(15): 47-57. Chang Yong, Yang Fufu,Hu Zhichao,et al. Research on Second Mechanisms Synthesis Task of Positive-Drive Disc Cam Mechanisms with Roller Follower Moving in General Planar Motion[J]. Journal of Mechanical Engineering, 2012, 48(15): 47-57. [3]常勇, 杨富富. 作平面运动滚子从动件形锁合凸轮机构的第Ⅱ类机构综合问题[J]. 机械工程学报, 2012, 48(1): 39-46. Chang Yong, YangFufu. Second Mechanisms Synthesis Task of Positive-drive Disc Cam Mechanisms with Roller Follower Moving in General Planar Motion[J]. Journal of Mechanical Engineering, 2012, 48(1): 39-46. [4]常勇, 李延平, 刘国祥. 按许用压力角设计最小尺寸作平面复杂运动滚子从动件平面凸轮机构的解析法[J]. 机械工程学报, 1991, 27(4): 37-41. Chang Yong, Li Yanping, Liu Guoxiang. The Analytics for Designing Minimum Size Disc Cam Mechanisms Whose Roller Follower Moving in General Planar Motion According to Allowable Pressure Angle[J]. Journal of Mechanical Engineering,1991,27(4):37-41. [5]常勇, 徐继杨, 黎庆. 推导凸轮廓线外凸性判据和曲率半径的一种新方法[J]. 黑龙江商学院学报(自然科学版), 1996, 12(2): 43-50.Chang Yong, Xu Jiyang, Li Qing. A New Method for Deriving the External-convexity Criterion and Convature Radius Formula[J].Journal of Heilongjiang Commercial College, 1996, 12(2): 43-50.[6]车林仙. 支撑函数法在作平面复杂运动平底从动件盘形凸轮机构设计中的应用[J]. 机械设计, 2002, 19(4): 10-12. Che Linxian. The Application of Support Function Method in the Design of Disc Cam Mechanism Whose Flat-bottomed Follower in the Form of Complicated Planar Motion[J]. Machine Design, 2002, 19(4): 10-12. [7]Schoenherr J. Synthesis of Planar Cam Mechanics with Lowest Dimensions[J]. Mechanism and Machine Theory, 1993, 28(3): 317-325. [8]Navarro O, Wu C J, Angeles J. Size -minimization of Planar Cam Mechanisms[J]. Mechanism and Machine Theory, 2001, 36(3):371-386. [9]华大年. 按许用压力角设计最小尺寸的摆动从动杆平面凸轮机构的解析法[J]. 机械工程学报, 1982, 18(4): 74-79. Hua Danian. The Analytics for Designing Minimum Size Disc Cam Mechanisms with Oscillating Follower according to Allowable Pressure Angle[J]. Chinese Journal of Mechanical Engineering,1982,18(4):74-79. [10]常勇, 吴从炘, 李延平. 关于《按许用压力角设计最小尺寸的摆动从动杆平面凸轮机构的解析法》一文的两点注记[J]. 黑龙江商学院学报(自然科学版), 1989, 5(2): 49-54. Chang Yong, Wu Congxin,Li Yanping. Two Notes on “the Analytics for Designing Minimum Size Disc Cam Mechanisms with Oscillating Follower according to Allowable Pressure Angle”[J]. Journal of Heilongjiang Commercial College,1989,5(2):49-54. [11]常勇, 吴从炘, 李延平. 关于《按许用压力角设计最小尺寸的摆动从动杆平面凸轮机构的解析法》一文的再注记[J]. 黑龙江商学院学报(自然科学版), 1990, 6(4): 15-19. Chang Yong, Wu Congxin, Li Yanping. The Further Notes on “the Analytics for Designing Minimum Size Disc Cam Mechanisms with Oscillating Follower according to Allowable Pressure Angle”[J]. Journal of Heilongjiang Commercial College,1990,6(4):15-19. [12]常勇, 杨富富, 李延平. 糖果包装机中凸轮连杆-组合机构的尺寸综合研究[J]. 中国机械工程, 2012, 23(17): 2023-2030. Chang Yong, Yang Fufu, Li Yanping. Research on Size Synthesis of Cam-linkage Mechanism in a Candy Packaging Machine[J]. Chinese Mechanical Engineering,2012, 23(17):2023-2030. [13]常勇, 林荣富, 李延平. 做平面运动滚子从动件盘形凸轮机构第Ⅱ类综合问题的广义化研究[J]. 中国机械工程, 2014, 25(5): 669-678. Chang Yong, Lin Rongfu, Li Yanping. General Class Ⅱ Synthesis of Disc Cam Mechanism with Roller Follower Moving in Palnar General Motion[J]. Chinese Mechanical Engineering, 2014, 25(5): 669-678. [14]常勇, 林荣富, 李延平. 做平面运动滚子从动件盘形凸轮机构的深度广义第Ⅱ类综合问题[J]. 中国机械工程, 2014, 25(16): 2149-2158. Chang Yong, Lin Rongfu, Li Yanping. General Class Ⅱ Synthesis of Disc Cam Mechanism with Roller Follower Moving in Palnar General Motion[J]. Chinese Mechanical Engineering, 2014, 25(16): 2149-2158. [15]Dasgupta A, Ghosh A. On the Determination of Basic Dimensions of a Cam with a Translating Roller-follower[J]. Journal of Mechanical Design, Trans. ASME, 2004, 126(1): 143-147. [16]Carra S, Garziera R, Pellegrini M. Synthesis of Cams with Negative Radius Follower and Evaluation of the Pressure Angle[J]. Mechanism and Machine Theory, 2004, 39: 1017-1032. [17]Ji Z, Manna Y A. Size Minimization of Disc Cams with Roller-followers under Pressure Angle Constraint[J]. Mechanical Engineering Science, IMechE, 2008, 222(12): 2475-2484. [18]王知行, 邓宗全. 机械原理[M]. 北京: 高等教育出版社, 2006. [19]吕庸厚, 沈爱红. 组合机构设计与应用创新[M]. 北京: 机械工业出版社, 2008. [20]林荣富,常勇.作平面运动滚子从动件盘形凸轮机构的第Ⅱ类凸轮轮廓设计[J].机械设计,2013,30(1):28-32. Lin Rongfu, ChangYong. Second Cam Profile Design of Disc Cam Mechanisms with Roller Follower Moving in Planar General Motion[J]. Machine Design, 2013,30(1):28-32. [21]林荣富,常勇.面向高速印刷机机构尺寸分析与综合的图谱方法[J].机械设计,2013,30(2):33-36. Lin Rongfu, Chang Yong. High Speed Printing Machine Mechanism Dimension Analysis and Synthesis Oriented at Las Method[J].Machine Design, 2013,30(2):33-36. (编辑王艳丽) Class Ⅱ Synthesis of Cam Mechanism with Floating Flat Faced Pushrod Li YanpingLin RongfuChang Yong Jimei University,Xiamen,Fujian,361021 Based on the configuration of high-speed printing machine mechanism with flat faced pushrod imported from German which was the evolution of the one with roller pushrod, the conceptions of “skew floating coordinate system”,“support function” and the ideas of “instantaneous one dimensional linear section” and its projection (the instantaneous interval set) were developed. Then, the important concepts of interval set on the rise,interval set on the return and the whole interval set, and the basic principles of solving the allowable selection area of instantaneous/whole flat axis and allowable range of the cam radiusr0were proposed. Furthermore, the whole common analytical formulas were derived and the analytical criterion of the solution existence and its existing form were obtained. The solution scope of the flat angle were searched and presented. Lastly, the problem of class Ⅱ synthesis of cam mechanism with floating flat faced pushrod were solved successfully and satisfactory. floating flat faced pushrod; skew floating coordinate system; support function; instantaneous one dimensional linear section; instantaneous/whole interval set; existing form 2013-07-18 国家自然科学基金资助项目(51475209,51175224);福建省自然科学基金资助项目(2010J01302,2006J0169) TH112.2DOI:10.3969/j.issn.1004-132X.2015.05.008 李延平,女,1963年生。集美大学机械与能源工程学院教授。研究方向为机构学、RE/RP/RT/CAE等。林荣富,男,1987年生。集美大学机械与能源工程学院助教。常勇(通信作者),男,1964年生。集美大学机械与能源工程学院教授。4 满足ρ>0条件的机构解的存在性与存在性态



5 满足α≤[α]∪ρ>0条件的机构解的存在性与存在性态


6 平底夹角σ的有解取值范围


7 机构综合示例
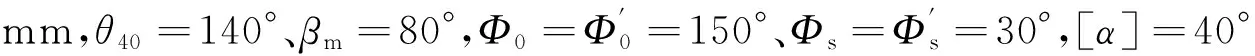


8 结语

