基于几何非线性有限单元法的温控器用片弹簧优化设计

陈文华　李小辉　潘　骏　贺青川　陈晓英,2　王　孟

1.浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州，3100182.衢州学院，衢州，324000

基于几何非线性有限单元法的温控器用片弹簧优化设计

陈文华1李小辉1潘骏1贺青川1陈晓英1,2王孟1

1.浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州，3100182.衢州学院，衢州，324000

利用几何非线性有限单元法对温控器用片弹簧参数进行了数值计算，并通过与实际测试结果的对比，验证了基于几何非线性有限单元法求解温控器用片弹簧参数的可行性和正确性。在此基础上，运用MATLAB优化工具，对片弹簧的结构尺寸进行了优化设计。然后建立触头弹跳的ADAMS仿真模型，并利用激光位移测试方法对模型进行了验证。最后利用ADAMS软件对温控器进行触头弹跳仿真分析。结果表明：基于几何非线性有限单元法优化设计的片弹簧能有效抑制动触头的弹跳。

几何非线性有限单元法；温控器；片弹簧；触头弹跳；优化设计

0　引言

温控器是实现温度控制的电开关元件，被广泛应用于温度控制电路中，因其触头材料有一定刚性，在通电过程中，难以避免因动触头与静触头间的碰撞而引起动触头的弹跳。动触头的弹跳是引起电弧，造成触头烧蚀的主要原因，会影响温控器的工作可靠性，并降低寿命[1-2]。文献[3-7]的研究结果表明，片弹簧的预压力和刚度等参数对动触头的弹跳有较大影响。在片弹簧的参数计算方面，罗依金[8]建立了片弹簧的弯曲微分方程，采用二次积分求解的解析方法对可简化为悬臂梁模型的直线形片弹簧进行了计算。该方法虽能精确得到片弹簧在力作用点处的位移，但仅适用于对形状简单、规则的片弹簧进行计算[9]。Fedder[10]和Peroulis等[11]通过对片弹簧的受力进行分析，计算出了簧片截面承受的弯曲力矩，建立了片弹簧沿长度方向的弹性位能计算模型。卢锦凤等[12]、翟国富等[13]基于变形能法，提出了离散复杂形体片弹簧、分段求解片弹簧柔度再线性叠加的思路。

上述求解方法均建立于小变形假设的基础之上，即在片弹簧的整个变形过程中，假设片弹簧的弹性变形量相对初始结构尺寸比较小，忽略因变形而引起的结构尺寸变化。但片弹簧属于薄壁元件，在一定载荷作用下会产生较大的位移，出现几何非线性问题，若继续基于小变形理论对片弹簧进行研究，将会产生比较大的误差[10，14]。目前研究片弹簧的几何非线性问题时通常借助于ABAQUS、ANSYS等有限元软件，但在将其应用在片弹簧的优化设计时，这些软件则存在分析计算不便、计算过程文件难以查看、求解耗时较长等缺点。

本文以温控器用片弹簧为研究对象，提出基于几何非线性有限单元法对其参数进行求解的数值计算方法，并与实测值进行对比验证。然后建立以片弹簧的预压力为目标函数，以片弹簧的刚度和最大弯曲应力为约束条件的优化模型，利用MATLAB软件中的fmincon优化函数进行优化设计。最后利用多体动力学分析软件ADAMS对温控器的触簧系统进行动态仿真分析，所得结果可为片弹簧的设计研究提供技术支撑。

1　几何非线性有限单元法

1.1物理模型

本文以型号为KSD 301的常闭式温控器为研究对象，其动作温度为90 ℃，复位温度为75 ℃，结构原理如图1所示。利用铆钉将片弹簧与底座固定，动触头铆接在片弹簧上。在电路处于接通状态时，片弹簧弯曲变形产生预压力P维持动静触头紧密接触。当外部温度升高到90 ℃左右时，温控器的碟形双金属片突跳，通过陶瓷杆对片弹簧产生推力，使动静触头分离，从而切断电路，推力所产生的机械能储存在片弹簧中。当温度降低到75 ℃附近时，碟形双金属片反向突跳，通过陶瓷杆作用在片弹簧上的推力消失，动触头闭合，触头之间的碰撞会使动触头发生弹跳。

1.碟形双金属片　2.静触头　3.动触头　4.陶瓷杆　5.片弹簧　6.铆钉图1　温控器的结构原理图

KSD301型温控器所用片弹簧包括三条直线段s1、s2、s3，其结构简图见图2，结构尺寸如表1所示。根据片弹簧的实际受力和约束情况，可认为铆钉铆接孔附近的平面未发生变形，所以可将其简化为平面梁系统。

图2　片弹簧的结构简图

l1(mm)l2(mm)l3(mm)宽度b(mm)厚度h(mm)折弯角β(°)折弯半径r(mm)10.01.65.03.70.18130.2

采用有限元方法对片弹簧建立如图3所示的有限元模型，图中数字为有限元节点编号。铆钉铆接孔中心在xy平面的投影位置为节点1，陶瓷杆与片弹簧的接触点为节点13，动触头铆接孔中心位置为节点15。节点1固定，节点15沿y轴负方向作用有预压力P，该点y方向的位移为δ，则节点15处的刚度：

(1)

图3　片弹簧的有限元模型

碟形双金属片突跳，通过陶瓷杆对片弹簧产生的推力为P1，作用于节点13。在P1作用下，片弹簧的弯曲变形最大，片弹簧的s2段产生最大弯曲应力：

(2)

式中，Mmax为片弹簧所受的最大弯矩。

1.2平面梁几何非线性有限单元法

对于节点i和j、长为l、截面积为A的梁单元，在局部坐标系下，其节点位移列阵可表示如下：

(3)

其中，u、v、θ对应着轴向位移、挠度和转角。

选择多项式作为位移的插值函数，插值函数的矩阵表达形式为[15]

(4)

式中，δe为单元节点位移向量。

略去梁单元的剪切变形，则其应变包括拉压应变εa和弯曲应变εb[15]，表示为

(5)

将式(5)代入式(4)，得

(6)

在大位移情况下，梁单元的应变和位移的关系式是非线性的[15]，可表达为

ε=(B0+BLδe)×δe

(7)

式中，B0为一般线性分析时的应变矩阵，与单元节点位移无关；BLδe为单元节点位移向量δe的函数。

由式(6)、式(7)可知：

(8)

(9)

根据虚位移原理：梁单元内应力由于虚应变dε所做的功等于外力在虚位移dδe上所做的功，若用φ表示内力与外力的矢量总和，在局部坐标系下，梁单元的平衡方程式为[15]

d(δe)Tφ=∫dεTσdV-d(δe)TR=0

(10)

式中，σ为单元应力；R为载荷列阵。

根据一般的线弹性关系,在不考虑初应力和初应变的情况下，可将式(10)简化为

(11)

式(11)中右边第一项可改写为

(12)

其中，k0为线性刚度矩阵，与单元的节点位移无关；kL为大位移矩阵，反映了单元位移的变化对平衡方程的影响情况[15]。

式(11)中右边第二项可表示为

(13)

式中，kσ为初应力矩阵。

记

kT=k0+kL+kσ

(14)

式中，kT为切线刚度矩阵。

根据式(12)～式(14)，将式(11)简化为

dφ=kTd δe

(15)

式(15)是梁单元在局部坐标系下的平衡方程，对于梁系统，应将式(15)中φ、kT和δe转换到整体坐标系下，再组装形成系统的失衡力向量ψ、切线刚度矩阵kT和节点位移向量δ，则对系统建立平衡方程式为

dψ=kTdδ

(16)

1.3方程的求解

牛顿-拉斐逊迭代法是求解非线性方程的常用方法[15]，其迭代格式如下：

kTnΔδn+1=R-F δn

(17)

δn+1=Δδn+1+δn

式中，F为系统的节点力向量。

具体迭代时，将以线性有限元法求解得到的节点位移向量δ0作为迭代求解的初始值，当节点15处y方向的位移变化率小于给定值时，迭代过程即可结束。

1.4片弹簧预压力的求解

以上求解过程是在已知外载荷的情况下实现对节点位移的求解的。根据温控器用片弹簧的结构特点和实际约束情况，当动静触头处于闭合状态时，片弹簧节点15处的y方向位移δ可通过计算近似得到，即δ≈l1sinβ，此时在节点15处产生的弹性变形力即为片弹簧的预压力P。

选取较小的预压力P0作为初始值，利用几何非线性有限单元法得到节点15处的y方向位移δ0，按照以下迭代公式对预压力P进行求解：

(18)

其中，kn为第n次求解的刚度。当|δn+1-δ|≤ξ时，迭代停止，ξ为给定的误差，此时得到的预压力Pn+1即是预压力P。

1.5最大弯曲应力的求解

片弹簧在推力P1作用下产生最大弯曲应力。对于KSD301型温控器，动静触头分开0.24 mm即可有效地切断电路。在P1作用下，片弹簧弯曲变形到稳定状态时，片弹簧节点15处的y方向位移δ可通过计算近似得到，即δ≈l1sinβ+0.24。同理按照式(18)的迭代格式可求解出推力P1的大小，进而按照几何非线性有限单元法确定出片弹簧所受的最大弯矩Mmax，由式(2)可求出最大弯曲应力σmax。

1.6理论计算与试验结果的对比

为了验证利用几何非线性有限单元法对温控器用片弹簧求解计算的可行性和准确性，现利用LDW-1型微机控制电子万能材料试验机对片弹簧进行压缩试验如图4所示。试验选取3个片弹簧试样，采用3次试验的平均值作为最终的试验结果。

图4　试验测试

利用变形能法[12]、线性有限单元法、几何非线性有限元方法，按表1所列的片弹簧尺寸参数，对节点15处的y方向位移δ进行求解计算。通过图5所示的结果可以看出，柔度法和线性有限单元法的求解结果比较接近，利用几何非线性有限单元法得到的求解结果最小。通过试验值的变化曲线可以看出：随着外载荷的不断增大，片弹簧的节点位移呈现出非线性增大的特点。利用变形能法和线性有限单元法得到的节点位移随着外载荷的增大保持线性增大的趋势，在外载荷大于0.9N时，求解结果与试验值的误差开始变得明显，并随着力的增大误差逐渐变大。利用几何非线性有限单元法得到的结果表明，变形位移与外载荷保持非线性增大的特点，与试验结果能够较好地吻合。

图5　求解结果与试验结果的对比

2　片弹簧的优化设计

2.1设计变量

选取表1所示的结构参数作为设计变量X：

X=(x1，x2，x3，x4，x5，x6，x7)=(l1，l2，l3，b，h，β，r)

设置变量的初始值和上下限如表2所示。

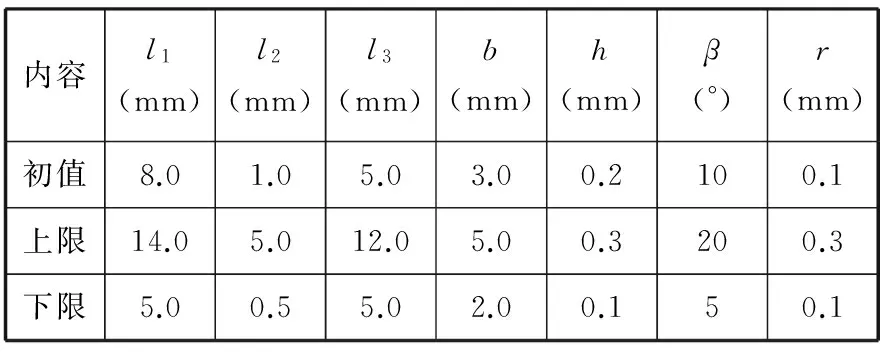
表2　设计变量的初始值和上下限

2.2目标函数

片弹簧的刚度和预压力等参数对动触头的弹跳有较大影响，在合适的范围内增大片弹簧的刚度和预压力能有效抑制动触头的弹跳，其中提高预压力值更为明显[7]。本文选取片弹簧的预压力作为目标函数。对可分断的电接触系统，预压力P与系统的电流i有关[1]，确定出预压力的范围为0.6～1.5N。最终确定出目标函数为

minf(P)=|P-1.5|

2.3约束条件

(1)根据温控器厂家的经验数据，片弹簧合适的刚度k范围为0.5～0.8 N/mm。为了缩短触头弹跳时间，应使片弹簧具有较大的刚度[7]。现选择片弹簧刚度k范围为0.7～0.8 N/mm。

(2)该型温控器所用片弹簧材料为铍青铜(QBe2)。片弹簧的最大弯曲应力应小于等于片弹簧材料的许用应力，即σmax≤[σ]=600 MPa。

(3)对于一般片弹簧，其宽度b和厚度h应满足2≤b/h≤10；为了避免片弹簧在弯曲处存在过大的应力集中，规定h/(2r)≤0.5；为了保证在预压力作用下，片弹簧节点15处y方向变形位移远大于s2段和s3段的y方向位移，规定l1在xz平面上的投影长度大于l3，即：l3≤l1cosβ。

2.4温控器用片弹簧的优化设计结果

现采用MATLAB软件中的可求解单目标约束优化问题的fmincon函数对温控器用片弹簧进行优化设计。应用几何非线性有限单元法对片弹簧的预压力、刚度等参数进行计算，优化后的结构参数如表3所示。

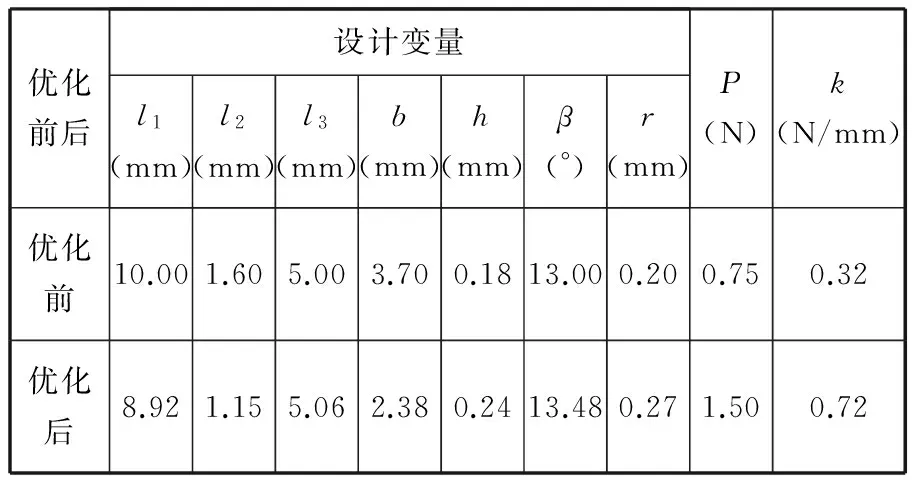
表3　优化设计前后结果对比

3　片弹簧优化设计结果的仿真验证

3.1仿真分析与试验验证

本文利用多体动力学分析软件ADAMS对突跳式温控器的触头弹跳运动进行仿真分析。首先利用有限元分析软件ANSYS生成片弹簧的模态中性文件，然后将其导入到ADAMS分析软件中。在动静触头之间添加接触，并采用碰撞函数法对其进行求解[2]，所得动触头运动参数求解结果如图6所示。

图6　动触头弹跳的仿真结果

由图6可知，动触头在闭合过程中的最大速度为291.6 mm/s，最大接触力为10.8 N，弹跳时间为4.3 ms。作用于片弹簧的外力消失后，储存在片弹簧中的变形能释放，动触头的动能不断增大，速度也不断增大。动静触头首次接触时，触头间的剧烈碰撞使动触头的速度急剧减小，触头间的接触力从零变为最大，动触头反向弹起。随着动触头动能的不断减小，动触头的弹起高度逐渐降低，直到动能被完全消耗，动触头才达到静止、稳定的闭合状态。

为验证仿真分析的准确性，对动触头的弹跳位移进行试验测试，所用仪器设备如图7所示。动触头闭合时的弹跳位移由LK-G80型激光位移传感器进行采集，经LK-GD500型控制器进行设置和处理后，输送到计算机中进行数据的记录和存储。

图7　试验测试示意图

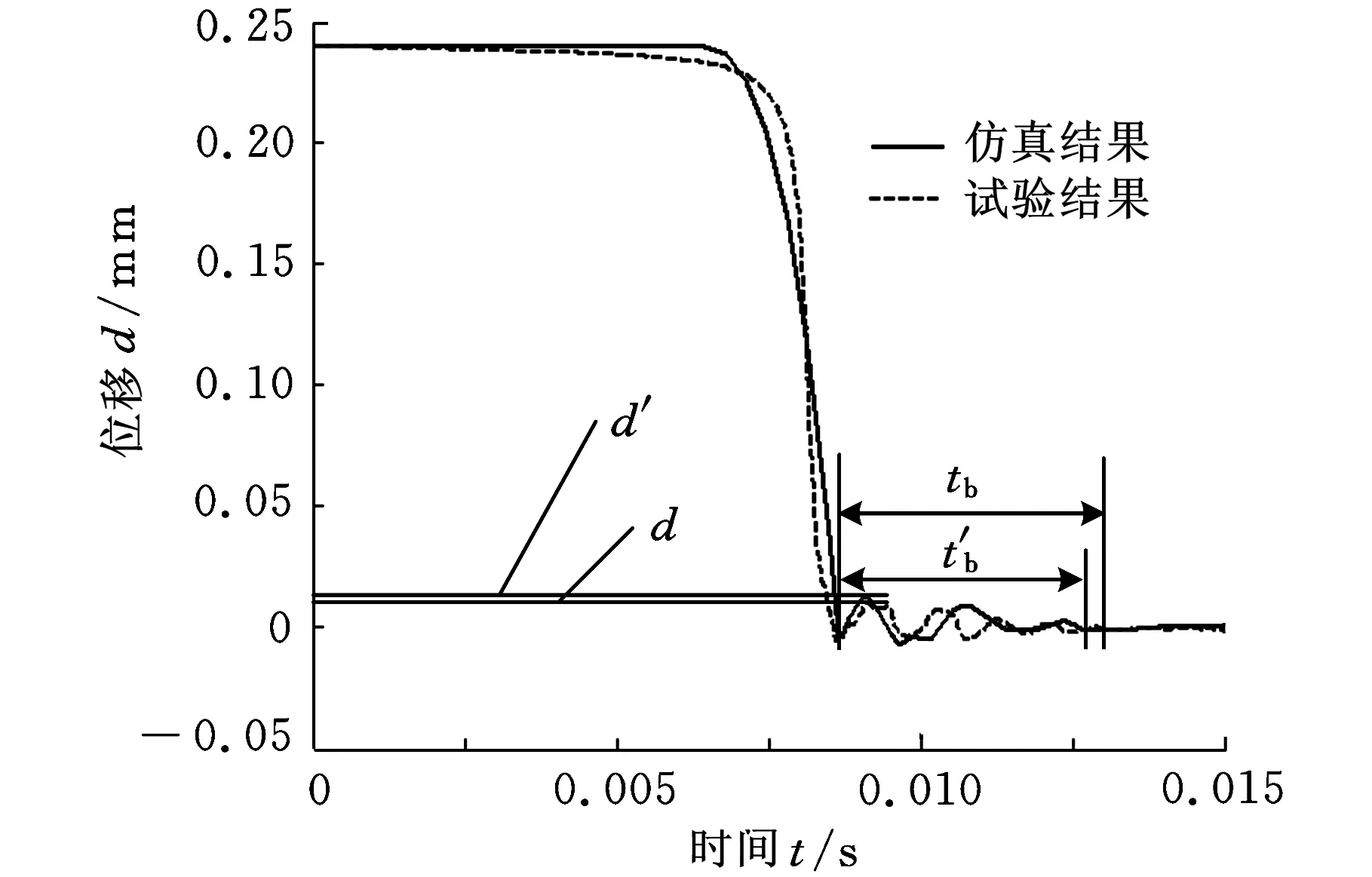
图8　触头弹跳位移对比

3.2优化结果的仿真分析

为检验经过优化设计后的片弹簧能否改善动触头的弹跳，将优化后的片弹簧导入到仿真模型中，并使模型中其他部件和接触力的参数与优化前的模型保持一致，得到的仿真结果如图9所示。

触头在弹跳过程中，弹跳时间越长，弹跳引起的电弧能量越大，对触头的烧蚀越严重[7]，由此引起的接触失效越容易发生，因此弹跳时间是评价触头弹跳的重要参数[2-7]。如图9所示，优化后的弹跳时间为2.3 ms，相对于优化前的片弹簧，弹跳时间缩短46.5%；对比图6和图9所示结果可知，优化前弹跳位移波动较大，位移变化剧烈，优化后的弹跳位移变化平缓，最大弹跳高度很小，说明动触头的弹跳得到抑制。

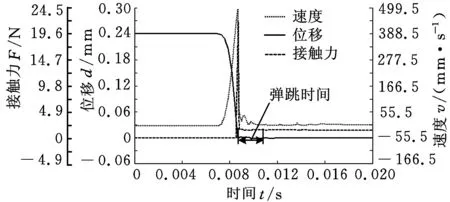
图9　优化后的仿真结果

由图9可知，对于优化后的触簧系统，触头闭合过程中的最大速度为499.5 mm/s，最大接触力为22.05 N，均大于优化前的触簧系统。这主要是因为优化后的片弹簧的预压力和刚度都变大，在动触头分开距离一定的情况下，优化后的片弹簧中储存的变形能增大，动触头的动能更大，导致触头间的碰撞更加剧烈。大的预压力和刚度会使触头的回弹变得更加困难，虽然触头间的瞬时冲击力变大，但该冲击力并不能大幅度地推动动触头，所以触头闭合瞬时的位移变化比较平缓，弹跳时间较短。

4　结论

(1)本文主要考虑片弹簧在外载荷作用下变形位移较大，引入几何非线性有限单元法求解，能反映出变形位移对结构平衡的影响，以此为基础对温控器用片弹簧进行有限元建模和求解。结果和试验值较为吻合，表明用几何非线性有限单元法对片弹簧进行分析更符合片弹簧的实际工作情况。

(2)由于动触头的碰撞弹跳与片弹簧的预压力有较大关系，为了改善动触头的碰撞弹跳性能，以片弹簧的预压力为目标函数，其尺寸参数为设计变量，运用几何非线性有限单元法，实现了对片弹簧结构的优化设计。

(3)为验证优化设计后的片弹簧是否能抑制动触头的弹跳，利用多体动力学软件ADAMS对动静触头闭合过程中的弹跳进行了仿真分析。结果表明，基于几何非线性有限单元法设计的片弹簧能有效抑制动触头的弹跳。

[1][1]程礼椿．电接触理论及应用[M]．北京：机械工业出版社，2004．

[2]熊军．航天继电器触簧系统接触弹跳及其影响因素研究[D] ．武汉：华中科技大学，2008．

[3]Mcbride J W，Sharkh S M．Electrical Contact Phenomena during Impact[J]．IEEE Transactions on Components, Hybrids and Manufacturing Technology，1992, 15(2):184-192．

[4]Li Y, Meguid S A, Fu Y, et al. Unified Nonlinear Quasistatic and Dynamic Analysis of RF-MEMS Switches[J]. Acta Mechanica, 2013,224(8): 1-15.

[5]LaRose III R P, Murphy K D. Impact dynamics of MEMS Switches[J]. Nonlinear Dynamics, 2010, 60(3): 327-339.

[6]McCarthy B, Adams G G, McGruer N E, et al. A Dynamic Model, Including Contact Bounce of an Electrostatically Actuated Micro-switch[J]. Microelectromechanical Systems, Journal of, 2002, 11(3): 276-283.

[7]纽春萍，陈德桂，李兴文 等．交流接触器触头弹跳的仿真及影响因素[J]．电工技术学报，2007,22(10):85-90．

Niu Chunping，Chen Degui，Li Xingwen. et al． Simulation of Contact Bounce of AC Contactor and Study of Its Influence Factors[J]．Transactions of China Electrotechnical Society，2007,22(10):85-90．

[8]罗依金．小型密封电磁继电器[M]．王蓉芳,译．北京：人民邮电出版社，1979．

[9]叶雪荣，梁慧敏，翟国富,等．电磁继电器簧片反力特性的通用计算方法[J]．低压电器，2007(3):10-12．

Ye Xuerong，Liang Huimin，Zhai Guofu，et al．Universal Calculation Method for Electromagnetic Relay Spring Force Characteristic[J]．Low Voltage Apparatus，2007(3):10-12．

[10]Fedder G K，Simulation of Microelectromechanical Systems[D]．California:University of California，1994．

[11]Peroulis D，Pacheco S P，Sarabandi K．Electromechanical Considerations in Developing Low-voltage RF MEMS Switches[J]．IEEE Transactions on Microwave Theory and Techniques，2003,51(1):259-270．

[12]卢锦凤，翟国富，刘茂凯．变形能法在计算继电器簧片柔度中的应用[J]．机电元件，1995(2/3):14-22．

Lu Jinfeng，Zhai Guofu，Liu Maokai．Using the Strain Energy Method to Calculate the Relay’s Flat Spring[J]．Electromechanical Component，1995(2/3):14-22．

[13]翟国富，樊薇薇，梁慧敏．基于均匀试验设计的航天电磁继电器触点滑移长度优化[J]．电工技术学报，2009,24(10):59-64．

Zhai Guofu，Fan Weiwei，Liang Huimin．An Optimization Method for the Contact Slip Length of Space Electromagnetic Relay Based on Uniform Experimental Design[J]．Transactions of China Electrotechnical Society，2009, 24(10):59-64．

[14]Fatola B O，Keogh P，Hicks B．Modelling Flat Spring Performance Using FEA[J]．Journal of Physics： Conference Series．IOP Publishing，2009,181(1):1-9．

[15]王勖成. 有限单元法基[M]. 北京：清华大学出版社, 2003.

(编辑王艳丽)

Optimal Design of Flat Spring Used in Thermostat Based on Geometrically Nonlinear Finite Element Method

Chen Wenhua1Li Xiaohui1Pan Jun1He Qingchuan1Chen Xiaoying1,2Wang Meng1

1.Zhejiang Province’s Key Laboratory of Reliability Technology for Mechanical &Electrical Product,Zhejiang Sci-Tech University,Hangzhou,310018 2.Quzhou University,Quzhou,Zhejiang,324000

A geometrically nonlinear finite element method was applied herein to the numerical calculation of the flat spring used in a thermostat. The calculation results were verified by comparison with experiments. Then the optimal design of the flat spring’s construction parameters were completed by using the MATLAB optimization toolbox. At last, the contact bounce of the thermostat was simulated by ADAMS. The results show that the flat spring which is designed optimally based on the geometrical nonlinear finite element method can prevent the contact bounce effectively.

geometrically nonlinear finite element method；thermostat；flat spring；contact bounce；optimal design

2014-02-27

长江学者和创新团队发展计划资助项目(IRT13097)；浙江省重点科技创新团队项目(2010R50005)

TM564.8< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.05.003

陈文华，男，1963年生。浙江理工大学机械与自动控制学院教授、博士研究生导师。主要研究方向为可靠性工程、机械传动与机构。李小辉，男，1990年生。浙江理工大学机械与自动控制学院硕士研究生。潘骏，男，1974年生。浙江理工大学机械与自动控制学院教授。贺青川，男，1984年生。浙江理工大学机械与自动控制学院讲师。陈晓英，女，1974年生。衢州学院机械工程学院副教授，浙江理工大学机械与自动控制学院博士。王孟，男，1989年生。浙江理工大学机械与自动控制学院硕士研究生。