加工时间不确定的柔性作业车间鲁棒调度方法
汪俊亮 张 洁 秦 威 银 莉 陈定方
1.上海交通大学,上海,200240 2.武汉理工大学,武汉,430063
加工时间不确定的柔性作业车间鲁棒调度方法
汪俊亮1张洁1秦威1银莉2陈定方2
1.上海交通大学,上海,2002402.武汉理工大学,武汉,430063
针对中小批量环境下加工时间不确定的柔性作业车间调度问题,采用冗余处理方法构建了以最大完工时间为目标的鲁棒调度模型。为降低算法的搜索规模和提高算法的求解速度,提出了顺序搜索机制,并设计两阶段遗传算法,分阶段获取冗余状态和最优结果。采用某柔性生产线的数据进行正交试验,优化了算法关键参数,并构建了柔性生产线仿真模型,对调度结果的鲁棒性和优化目标性能进行了分析。结果表明,该算法在目标性能和鲁棒性上都显著优于标准遗传算法,能有效处理加工时间不确定的柔性作业车间调度问题。
加工时间扰动;柔性作业车间;鲁棒性;顺序搜索
0 引言
不确定因素作用下的柔性作业车间调度问题是在柔性作业车间调度问题(flexible job-shop scheduling problem,FJSP)的基础上,考虑车间环境的随机性和动态性,处理不确定因素对调度目标影响的一类调度算法,是车间调度领域的一类关键问题。实际的生产环节中,由于生产环境具有动态性和随机性,导致加工时间、工件到达时间和机床故障率等因素很难用一个确定的值来描述[1],因此,建立在调度参数确定情况下的柔性作业车间调度方案已经难以满足生产的需求。与此同时,不确定因素扰动下的柔性作业车间调度问题受到越来越多研究者的关注,成为目前FJSP领域的研究热点之一[2]。
对于不确定因素扰动下的作业车间调度方法主要分为动态重调度和静态预调度两类[3]。采用动态重调度方法会反复产生重调度方案[4],对扰动因素进行处理时,虽然方案具有较好的时效性,但是频繁地修正生产计划,对物料计划、人员派遣会产生连锁反应,从而造成生产混乱。静态预调度方法是提前考虑不确定因素对于调度结果的影响,提前对调度结果作出修正,但是如何对不确定因素的扰动进行描述和预测,是预调度中的一大难题。
制造过程中不确定因素的处理方法主要有随机数学方法、模糊数学方法、冗余处理方法等。Xia等[5]采用随机数学方法处理加工时间不确定的单机调度问题,设计惩罚函数对超期和提前问题进行处理。但是随机数分布往往通过大量历史数据的分析获得,而大量生产数据的统计在中小批量的生产模式中难以实现。李平等[6]采用三角模糊数来处理加工时间不确定的Job Shop问题时,运用隶属度函数将连续的大数据量问题转化为离散的小数据量问题来处理。但是其隶属函数的构造对历史数据具有较强的依赖性,并不适用于产品种类多、变化快的中小批量生产模式。Zhang[7]采用冗余处理方法中的最小最大遗憾方法对批量生产环境下,需求不确定的调度问题进行求解。但是该方法计算规模较大,在处理大型问题时难以实时求解。
国内外学者大多对大批量作业车间的不确定因素处理进行研究。鲁建厦等[8]针对加工时间不确定的批量混合装配车间调度问题进行研究,运用随机数学理论对实际作业时间的波动情况进行处理; Ponsich等[9]对加工时间不确定情况下的大批量生产调度问题,采用了遗传算法进行求解。Hufner等[10]针对大批量产品生产调度问题,采用了随机整数规划方法进行处理。综上可知,学者们对于大批量问题的研究较为充分,而对于多品种小批量生产模式下的研究较少。但是,多品种小批量的作业模式因为其产品覆盖广、作业柔性高,被广泛应用于我国中小型制造业中,因此,针对多品种小批量环境下,不确定因素扰动的作业车间鲁棒调度问题具有重要意义。
本文针对多品种小批量生产模式下,加工时间不确定的柔性作业车间调度问题进行研究,采用基于冗余处理的方法处理加工时间不确定的波动问题,并建立了鲁棒预调度模型。设计了两阶段遗传算法,依次获取了问题冗余解和最优解,为缩小搜索规模,设计了顺序搜索机制,简化了搜索方式,使复杂环境下的鲁棒调度算法具有了较大的应用潜力。
1 问题描述与模型建立
多品种小批量环境中,加工时间不确定的柔性作业车间调度问题具有如下特点:加工柔性高,零件种类多样多变、数量较少,工序加工时间的变化规律难以通过历史数据的统计分析得到但其大致的区间可以通过预估确定。
对于三种常用的不确定因素处理方法(随机数学方法、模糊数学方法、冗余处理方法)进行分析和对比可知:随机数学方法需要大量历史数据来构建分布函数,模糊数学方法需要历史数据来构建隶属度函数,这两种方法对历史数据依赖性大,不适用于柔性作业车间的生产模式,因此采用冗余处理方法建立数学模型。
加工时间不确定的冗余处理方法通过对加工时间进行抽样,取样本中的目标函数值和最优情况偏离最大的情况,即最大冗余情况作为调度求解中不确定因素的扰动状态,并在此状态下,对调度问题进行求解,其原理如图1所示。冗余调度方法是在最劣的时间样本下求取最优调度方案,确保在各种加工时间场景下,最优方案具有鲁棒性和性能指标的优势。

图1 加工时间不确定的冗余处理方法
1.2基于冗余机制的鲁棒预调度模型建立
以柔性作业车间为对象,采用冗余调度方法,以最大完工时间为目标,构建考虑加工时间不确定变化的鲁棒调度模型:
为了进一步证明本文提出的行为识别方法的可行性,本文还在MSRC-12数据集上进行实验,动态行为最终平均识别准确率为78%。文献[15]采用随机森林算法进行动作分类,同样在MSRC-12数据集上进行测试,平均识别准确率为67.3%,对比可知本文方法识别准确率更高。
(1)
i=1,2,…,n;j=1,2,…,m
约束函数:
Ci1≥Pi1
(2)
|Ci1j1k-Ci2j2k|≥(1-Qi1i2k)Pi2j2+xi1i2kPi1j1
(3)
i1,i2=1,2,…,n;j1,j2=1,2,…,m;k=1,2,…
Cij-Ci(j-1)≥Pij
(4)
S={P11P21…Pn1P12P22…
Pn2…P1mP2m…Pnm}
(5)
(6)
式(1)表示目标函数为在最大冗余情况下最大完工时间达到最小时所对应的调度方案,式中X为工序调度方案的集合,S为每一道工序加工时间的集合,Cij为第i个工件、第j个工序的完工时间;式(2)表示工件的起始加工约束,表示任何工件都要求在0时刻以后开始加工;式(3)表示同一时刻同一机器只能加工一个零件,Ci1j1k表示机器k上加工的零件i1的第j1道工序的完工时间,Pi1j1表示零件i1的第j1道工序的加工时间,Qi1i2k表示机器上工序的排列顺序,其取值情况如下:
(7)

2 基于顺序搜索机制的两阶段遗传算法
2.1基于冗余调度模型的顺序搜索机制
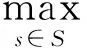
目前,常采用两层次嵌套的方法求解基于冗余处理的鲁棒调度[3]。对于n个工件m道工序p个机器的柔性制造系统调度问题而言,共需计算qkn×mpn×m次,其中k为加工时间样本数量,q为一次方案求解需要的计算次数,该遍历方法随问题规模增长呈指数增长,难以适应复杂问题的求解。
为提高鲁棒调度算法的求解速度,根据下述引理[11],采用顺序搜索结构搜索最优解。


由引理1和引理2可知,当f(x,s)取得可行解时,FJSP种群的最优解x1,可以同时和加工时间进化种群的最优解s1、s2配套实现最优,即两个种群的搜索进化可以互为依托,同步进行。基于此,本文采用基于顺序搜索的方式,实现快速求解。2.2两阶段遗传算法设计
基于顺序搜索机制设计两阶段遗传算法对问题进行快速求解,其流程见图2。在第一阶段算法中,在FJSP种群空间中对加工时间种群进行搜索获取最大冗余状态;在第二阶段算法中,在加工时间种群中对FJSP种群进行搜索优化,获取最优调度结果。两阶段算法互为依托,反复搜索进化,得到最优解。
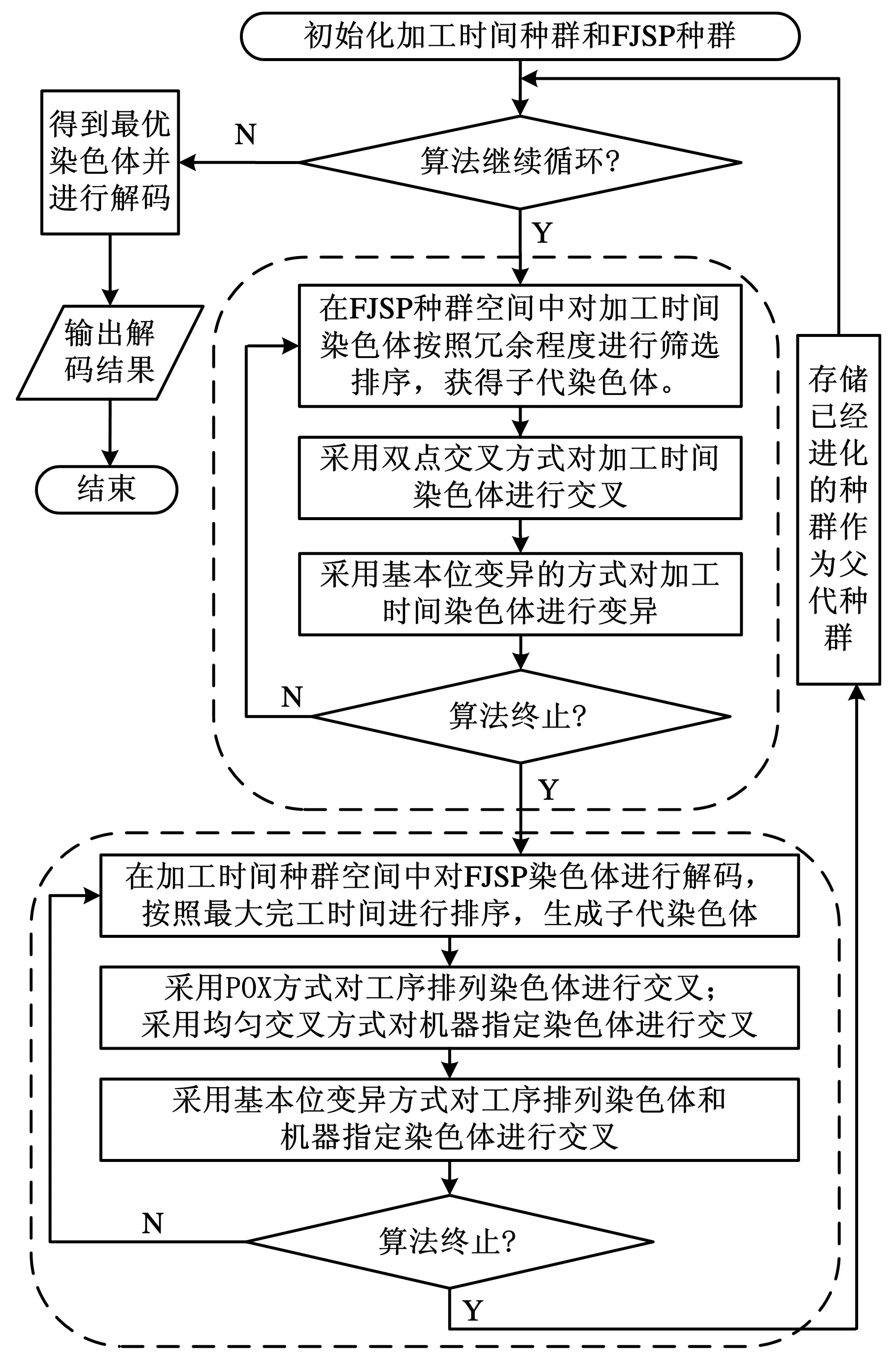
图2 采用顺序搜索的快速求解算法流程图
对于采用顺序搜索机制的算法,对其效率分析如下:假设染色体种群数均为N,每一次解码需要计算p次,遗传算法总共迭代计算M次,则总共需要计算机计算2MpN次。通过对比可知,采用顺序搜索的求解方式在搜索速度上达到了乘数级别,相比传统的嵌套求解方式在求解速度上具有巨大的优势。
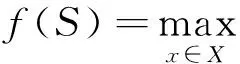
3 案例分析
采用某公司柔性生产线实际案例对算法进行正交试验,优化算法关键参数。同时为分析算法输出方案的鲁棒性和目标性能,将标准遗传算法与本文的鲁棒调度算法输出结果进行比较,并在eM-Plant环境下建立仿真调度模型,对算法输出方案鲁棒性进行评价。
3.1参数优化和求解
采用武汉某柔性生产线10个工件、3步工序、4台机器的实际完全柔性作业案例作为源数据,采用正交试验法对遗传算法中的POX交叉概率、双点交叉概率、均匀交叉概率进行优化。对POX交叉概率的三个水平分别为A1=0.3、A2=0.5、A3=0.7,双点交叉概率的三个水平分别为B1=0.4、B2=0.6、B3=0.8,均匀交叉概率的三个水平分别为C1=0.4、C2=0.6、C3=0.8三种情况下的算法运行结果依次进行正交测试,测试结果见表1。
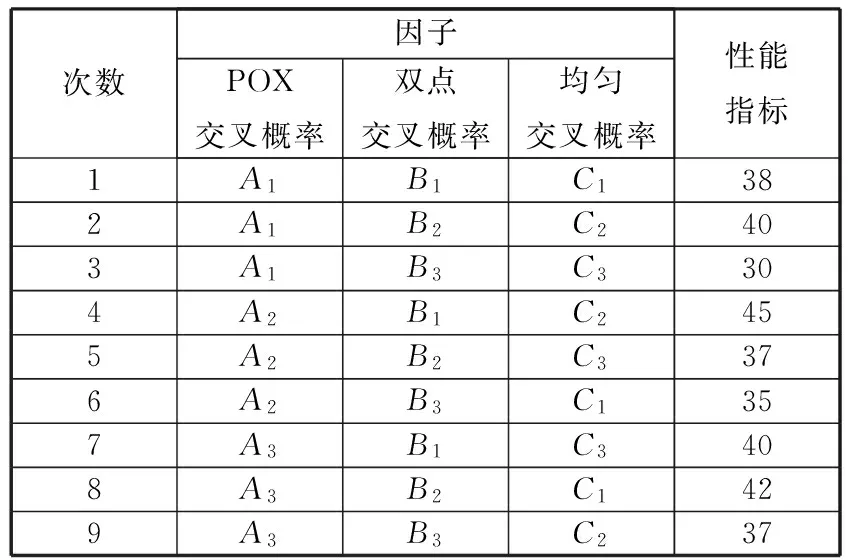
表1 正交试验结果
为了直观显示测试结果,将数据经过处理之后以图的形式表示,如图3所示。
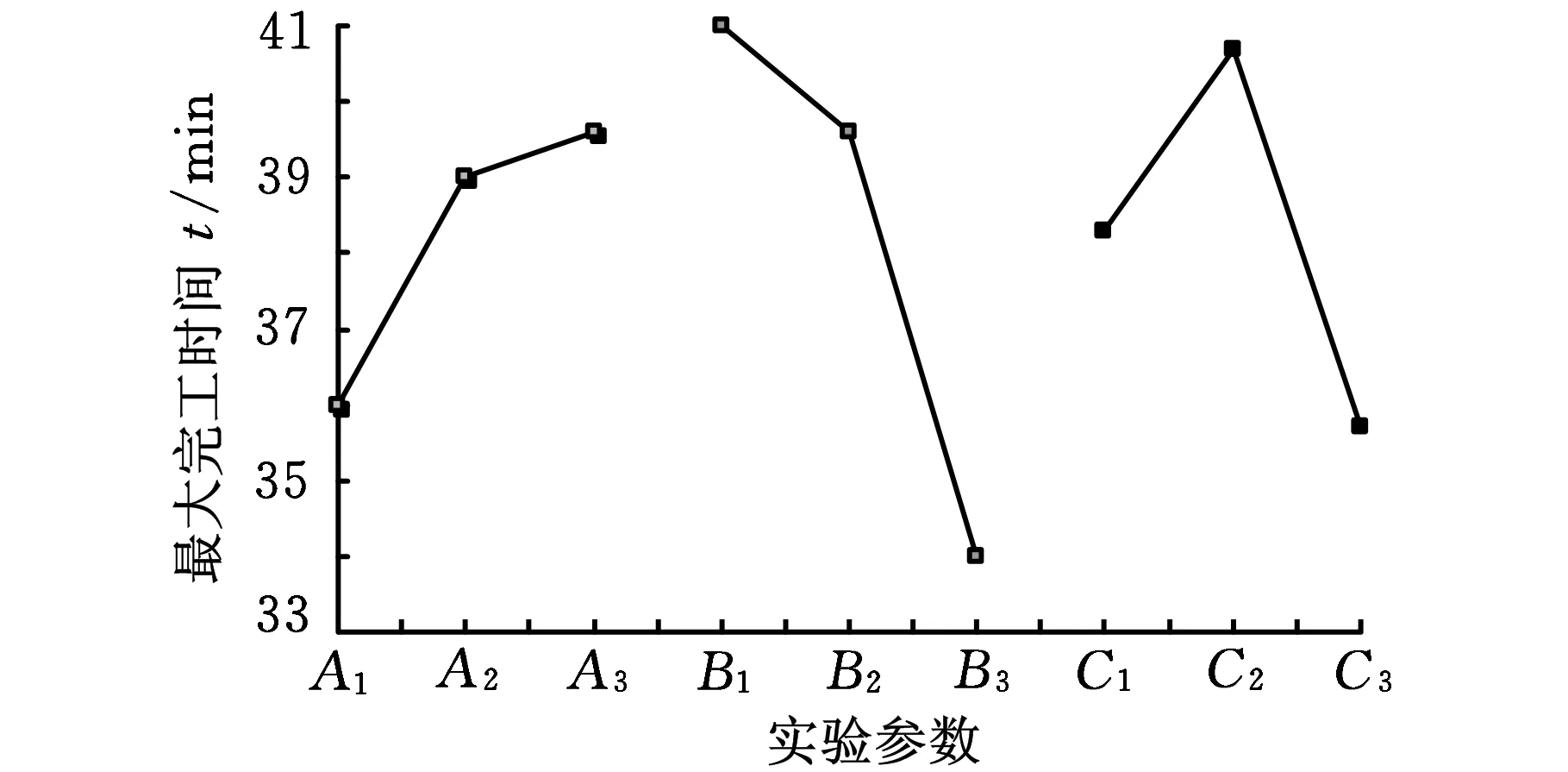
图3 算法参数正交试验结果

图4 本文鲁棒调度算法FJSP实例预调度方案
通过参数测试结果发现,POX交叉概率为0.5,双点交叉概率为0.8,均匀交叉概率为0.8时,算法性能表现较好。在此基础上,设置其他参数如下:重调度种群规模为20,变异概率都设置为0.005,循环次数设置为100,调度结果见图4。程序在CPU:CORETMi7-2.0 GHz,RAM:4GB的环境下运行。
采用标准遗传算法和本文提出的鲁棒算法进行对比,采用相同的算法参数并在相同环境下对同一问题进行计算,其输出方案见图5。
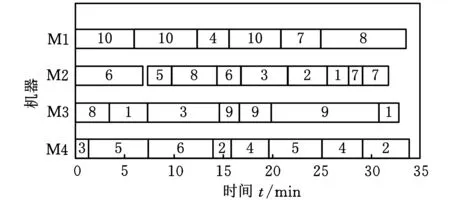
图5 标准遗传算法求解FJSP实例调度方案
3.2调度方案仿真与分析
在完成算法的求解之后,对方案的鲁棒性进行评价。常见的鲁棒性评价方式有:随机数学计算法、离散事件仿真法。Rahmani等[12]采用随机数学原理模拟不确定因素发生,从而计算方案的鲁棒性。但是其参数的数值根据经验设定,在复杂因素影响下欠缺数据的真实性。因此,本文采用离散事件仿真的方法,评价方案的鲁棒性。首先定义车间调度方案的鲁棒性如下:
R(s)=r·E(M(s))+(1-r)·E(δ(s))
(8)
其中,M(s)是一个随机变量表示不确定因素影响下实际的最大完工时间;δ(s)=|M(s)-Mo(s)|表示预期最大完工时间和实际最大完工时间之间的差值;r是权重函数,其值在(0,1)之间。由于Mo(s)是确定的,M(s)和δ(s)的期望值等同于E(M(s))=E(δ(s))+Mo(s)。因此作业车间调度方案的鲁棒性可以等同为
R(s)=r·E(Mo(s))+E(δ(s))
(9)
在计算R(s)的基础上,对鲁棒性进行分析,采用R(s)和r·E(Mo(s))的接近程度反映调度方案的相对鲁棒性,计算得其偏差为
(10)
采用R(s)与平均单机工序工时之和r∑(T/4)的偏差反映该方案实际性能与目标性能的偏差:
(11)
在eM-Plant环境中建立仿真调度模型,对算法输出方案进行分析。归纳出工件的约束关系和加工时间数据(表2),作为仿真数据的输入。

表2 工序加工时间数据及机器分配方案 min
对仿真模型多次运行,并将结果和未考虑加工时间不确定的柔性作业车间的调度方案进行对比。其计算结果如表3所示(其中r=0.7)。
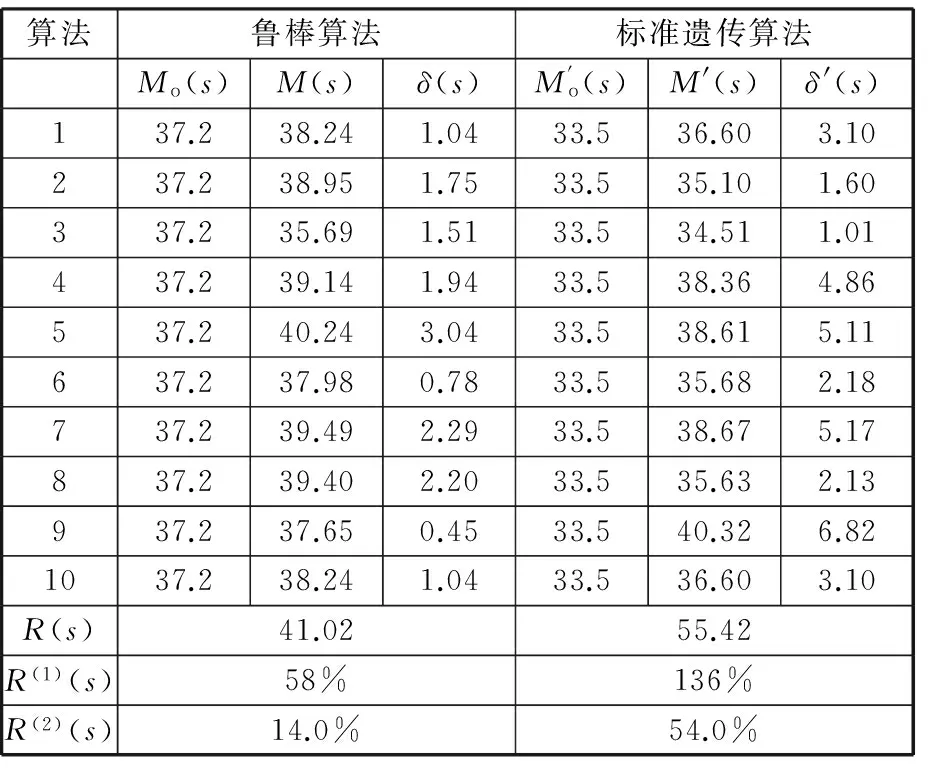
表3 调度方案鲁棒性评价结果
分析可知,在加工时间不确定情况下,本文提出的算法产生的方案在相对鲁棒性和实际性能上都有较好的表现,在对不确定性作出有效的规避的同时发挥了良好的调度性能。
4 结语
本文针对中小批量环境下加工时间不确定的柔性作业车间调度问题,结合冗余处理方法构建鲁棒调度模型,并提出顺序搜索机制,降低搜索规模。对算法参数进行优化和修正,并进行了仿真实验。该算法的主要特性有以下两点:①普适性。算法采用冗余处理方法构建模型,对加工历史数据依赖性低,算法稍作调整,便适用于其他的车间调度问题。②快速性。算法针对两层嵌套结构,创新采用顺序搜索机制,有效减少了计算量,在乘数时间内获得不确定因素扰动下的调度方案。
综合考虑本文的工作和领域的发展,进一步的研究可以关注于以下两点:①增加算法在复杂问题下的性能分析实验和同类算法之间的对比实验;②对多种不确定因素耦合作用下的车间调度问题进行研究。
[1]Van S,Demeulemeester L,Herroelen W. A Classification of Predictive-reactive Project Scheduling Procedures[J]. Journal of Scheduling, 2007, 10(3): 195-207.
[2]陈庭贵,琚春华.多干扰的资源约束项目调度问题[J].计算机集成制造系统,2012,18(11):2409-2418.
Chen Tinggui,Ju Chunhua.Resource-constrained Project Scheduling Problem with Multi-factor Disruptions[J].Computer Integrated Manufacturing System,2012,18(11):2409-2418.
[3]Herroelen W,Leus R.Robust and Reactive Project Scheduling: a Review and Classification of Procedures[J].International Journal of Production Research,2004,42(8):1599-1620.
[4]Novas M, Henning P. Reactive Scheduling Framework Based on Domain Knowledge and Constraint Programming[J]. Computers & Chemical Engineering, 2010, 34(12): 2129-2148.
[5]Xia Y, Chen B, Yue J. Job Sequencing and Due Date Assignment in a Single Machine Shop with Uncertain Processing Times[J]. European Journal of Operational Research, 2008, 184(1): 63-75.
[6]李平,顾幸生.不确定条件下不同交货期窗口的JobShop调度[J].管理科学学报,2004,2:22-26.
Li Ping, Gu Xingsheng. Job Shop Scheduling with Uncertain Processing Time and Distinct Due Windows[J]. Journal of Management Sciences in China, 2004,7(2): 22-26.
[7]Zhang M. Two-stage Minimax Regret Robust Uncapacitated Lot-sizing Problems with Demand Uncertainty[J]. Operations Research Letters, 2011, 39(5): 342-345.
[8]鲁建厦,施锦峰,李修琳,等.一类已知概率分布下的混合车间鲁棒调度问题研究[J].中国机械工程,2010,21(19):2328-2333.
Lu Jianxia, Shi Jingfeng, Li Xiuling, et al. Study on Hybrid Shop Robust Scheduling Problem with Known Probability Distribution[J]. China Mechanical Engineering, 2010, 21(19): 2328-2333.
[9]Ponsich A, Bonfill A, Espua A, et al. Genetic Algorithms for the Scheduling of Multiproduct Batch Plants within Uncertain Environment[J]. Computer Aided Chemical Engineering, 2007, 24: 619-624.[10]Hufner M, Tometzki T, Engell S. Two-layer Planning and Scheduling of Batch Production Processes under Uncertainty[J]. Computer Aided Chemical Engineering, 2009, 27: 1197-1202.[11]Jensen T.Robust and Flexible Scheduling with Evolutionary Computation[D].Arhus:University of Arhus,2001.
[12]Rahmani D, Heydari M. Robust and Stable Flow Shop Scheduling with Unexpected Arrivals of New Jobs and Uncertain Processing Times[J]. Journal of Manufacturing Systems, 2013.
(编辑王艳丽)
Robust Scheduling on Flexible Job Shop with Uncertain Processing Time
Wang Junliang1Zhang Jie1Qin Wei1Yin Li2Chen Dingfang2
1.Shanghai Jiao Tong University,Shanghai,200240 2.Wuhan University of Technology,Wuhan,430063
This paper investigated the flexible job-shop scheduling problem (FJSP) with uncertain processing time in a multi-type and low-volume environment. A minimax regret based robust scheduling model was built to minimize the makespan. A novel sequential search rule was put forward to reduce the calculation amount of the algorithm and a two stage genetic algorithm was designed to figure out the redundant and optimal solutions. Orthogonal test was designed to optimize significant parameters, and then, a simulation model was established to evaluate the robustness and objective performance of the algorithm. The results show the proposed algorithm has a better performance than genetic algorithm on flexible job-shop scheduling problem under uncertain and dynamic environment.
processing time disturbance; flexible job-shop; robustness;sequential search
2013-12-23
国家高技术研究发展计划(863计划)资助项目(2012AA040907)
TH166DOI:10.3969/j.issn.1004-132X.2015.05.010
汪俊亮,男,1991年生。上海交通大学机械与动力工程学院硕士研究生。主要研究方向为制造系统建模与优化、虚拟制造。张洁(通信作者),女,1963年生。上海交通大学机械与动力工程学院教授。秦威,男,1985年生。上海交通大学机械与动力工程学院博士。银莉,女,1990年生。武汉理工大学能源与动力工程学院硕士研究生。陈定方,男,1946年生。武汉理工大学智能制造与控制研究所教授。

